转子非平稳状态的计算阶比-全息谱方法研究
倪雨晨/中船重工705所海源测控技术有限公司
廖与禾马再超刘庆成/西安交通大学机械工程学院
转子非平稳状态的计算阶比-全息谱方法研究
倪雨晨/中船重工705所海源测控技术有限公司
廖与禾马再超刘庆成/西安交通大学机械工程学院
针对转子振动信号的频率在非平稳情况下难以采用传统频谱分析方法提取频率特征的问题,提出了将全息谱原理和计算阶比分析理论相结合的计算阶比-全息谱分析方法。计算阶比分析用于调频信号的角域重采样,并提取需求阶次特征;全息方法用于表达幅值变化规律。通过实验模拟正常转子、裂纹转子和不对中转子的启车状态信号,结果表明:该方法能够实现非平稳状态下故障特征信息的提取,为实际生产过程中的状态监测、故障诊断、评估提供参考和依据。
阶比分析;全息谱;等角度采样;转子;故障特征提取
0 引言
机械故障诊断技术是机械工程中一门很重要的学科,其中一个研究内容就是对旋转机械设备的运行状态进行监测,从而对可能发生的故障类型进行识别和诊断,以便为这类设备的安全运行提供可靠保障,许多生产实践证明故障诊断与状态监测技术研究对工业生产具有重要的现实意义[1-2]。
目前旋转机械故障诊断主要是基于系统的稳态振动特征,如稳态振动时的轴心轨迹、频率,转频、倍频、分频的幅值和相位等,但对升、降速非平稳过程中的振动信息利用还存在不足。由于启停车过程的振动信号相当于一个宽频激励下的动态响应,与稳定转速过程相比,其振动信号中包含的信息更为丰富,对机组的动态特性的反应也更为直接和深入。但启停车过程中转速的不断变化意味着信号是非平稳的,直接使用FFT(傅里叶变换)会出现频率模糊的现象,严重影响了后续全息谱分析的精度[3]。另外,油膜涡动及油膜振荡等故障会造成振动过大或振幅过大,且其通常在变转速下发生,常规的频谱分析无法准确提取其故障特征信息[4]。而且旋转机械的转子由于零部件制造误差、装配误差以及材质不均匀、运行磨损不均匀等原因也会造成转子的不平衡[5];因此,针对这类信号的分析必须采用能够处理非平稳信号的方法。
我们常用的传统的全息谱技术侧重于对转子稳态运行信息分析,而对转子升降速过程的启停车非稳态信息利用不足,此时不同机理故障稳态响应的相似性会导致故障误诊或漏诊。为了拓展全息谱技术的应用范围,实现变速过程故障响应的特征参数提取,本文将计算阶比分析引入全息谱分析过程,实现了转子非稳态信息特征提取和利用,提出一种阶比-全息谱的分析方法。
该方法避免了FFT的频率模糊问题,并构造阶比全息瀑布图实现转子典型故障特征的显式表达与在线识别。通过在转子实验台模拟不对中和裂纹等典型故障,验证了该方法对于非稳态信息的处理和故障识别能力。
1 基本理论简介
1.1 全息谱基本原理
全息谱构造了多支承转子系统的单一截面的分析方法,并且也巧妙的构造了整机振动的分析方法。它运用了内插技术,在自由方式(非等转角间隔整周期)下非常精确的求出了采集到的振动信号的幅值、频率以及相位值,接着将转子垂直方向这三个信息集成,最后不同频率分量下转子的振动行为就是用所合成的一系列椭圆来刻画的全息谱技术。要求参加融合的各组数据必须具有相同的采样频率、数据长度以及相同的时间起始点,并且具有大体相近的信噪比,即各个传感器所输出的数据必须具有高度的均一性,原因是它在数据层上将同一个转子的各个轴承截面上布置的传感器所提供的信息加以融合[6]。
全息谱分别将x,y两个方向上的振动谱分析之后,融合各个频率成分下x,y两个方向上的振动,将谱分析方法和轴心轨迹分析方法相结合,得到主要频率分量的频率、幅值及相位,并在转子测量面上分别对垂直和水平两个方向的振动信号进行傅里叶变换,之后在一张谱图上按照各个主要频率合成并排列得到全息谱图[7],见图1。

图1 全息谱传感器的两种安装方式图
若转子截面两个方向振动信号的第i个主要频率分量的参数方程为:

式中:ai,βi是第i主要频率的相位;Ai,Bi是第i主要频率的幅值;fi是主要频率分量的旋转频率。
因此将转子某个测量面上水平和垂直两方向的振动信号分别进行FFT,得到主要频率分量的频率幅值和相位,然后利用各个主要频率的幅值和初相位绘制出对应频率分量的全息椭圆并且排列在一张谱图上即形成二维全息谱,见图2。

图2 二维全息谱构建图
1.2 计算阶比分析
计算阶比分析技术分为有转速计和无转速计两种类型,本文采用有转速计的计算阶比分析技术,它具有精确度高,计算量小和方法简单等优势[8],原理示意图见图3。对等角度间隔的振动序列进行FFT等方法获取的阶比-幅值谱称为阶比谱。所以,为了利用计算阶比方法计算阶比谱,采用的振动信号必须为角域信号,因此必须将等时间间隔采样后的信号通过处理实现等角度重采样转换,同时,等时间间隔采样方法需要抗混叠滤波和角域重采样算法。计算阶比分析技术其核心是实现振动信号的等角度采样,即无论转速如何变化,每一转采样的点数总是相同,以保证可以整周期采样。因此在忽略幅值变化的情况下,信号在角域上可看作是平稳信号,就可以对非平稳状态下的转速波动或升降速等过程信号进行角域上的傅里叶变换。

图3 计算阶比原理示意图
在等时间采样中,随着转速增加,每一圈的采样点数和采样位置是变化的,原理如图4。而由图5可看出,在等角度采样中,即使转速增加,但每一圈的采样点数不变。

图4 等时间采样原理图

图5 等角度采样原理图
1.2.1 采样频率和抗混叠滤波器截止频率参数的设定
为了避免发生频率混叠,不使原有信号的有效信息丢失,采样时应满足尼奎斯特采样定理:

式中:fs是采样频率;fm是模拟信号的最高分析频率。由于实际信号中可能包含频率很高的信号成分和高频噪声,但fs不能因为有高频信号而无限高,所以需要将高频率部分滤除后再进行采样,引入抗混叠滤波。如果不滤除,信号中的高频率部分会以采样频率为界限折叠到低频段部分,出现不准确的频率成分而引发后续错误的分析结果。
抗混叠低通滤波器的截止频率fc等于需要分析信号成分的最高频率fm。则截止频率fc与采样频率fs的关系如式(3)、(4)所示:

旋转机械振动的特征是各振动分量的振动频率为转速的倍数或分倍数。设轴的转速为7 200r/min即120Hz,则一般对120Hz的整数倍频率进行分析,这个120Hz的整数倍频就是阶比。阶比与转速的关系如下式,旋转机械最高转速为Rm,需要分析的最大阶比为Lm,则最高频率为fm满足式(5)。

1.2.2 跟踪滤波器参数设定
在大型旋转机械的启停车过程中,转速的变化范围通常很大。若以机械旋转的最高转速来设置滤波器的截止频率,则在低转速时可能会出现频率混叠,无法作出阶比图和全息谱图。同样,若以最低转速设置滤波器频率,则在高转速时有用的频率成分可能被滤除。因此抗混叠滤波器的截止频率不能一直固定不变是某个数,需要进行实时跟踪滤波。在实际进行阶比分析时,需要实时根据转速信号来调整抗混叠滤波器的截止频率。将高于分析阶比的信号滤除,避免频率混叠。文章后续的3.1部分对此作出了验证。
1.2.3 计算等角度时间序列
等角度重采样理论主要原理是时域到角域的重采样[9]。先用转速信号来确定各等角度的时间序列,然后用插值拟合的方法确定对应振动信号的幅值大小[10-11]。重采样用相同时间采样到的数据被再次采样到角域,这个过程中应用了自适应数字重采样算法[10]。
等角度时刻的计算方法:在较短的一段时间内如旋转机械转动一周的时间内,假定转速是均匀增加或均匀减小的,则转过的角度与时间成一元二次关系,即:

式中的b0,b1,b2是未知的,可用t1,t2,t3三个脉冲发生时刻所对应的(0,2π,4π)来联立求解:

将θ离散为kΔθ,代入即可求出各等角度的时间序列。具体分以下两种情况:

2)当b2=0时,在三个脉冲内做均速转动,等角度时间序列计算式如(9)所示:

求出各等角度时间序列后,根据原来的等时间间隔时振动信号的幅值通过样条差值幅值拟合[12]的方法,即可得到重采样后各等角度时间序列的幅值。
2 计算阶比方法流程说明
由图6所示流程可归纳出转子阶比分析的具体步骤如下:
步骤1:同步等时间间隔采集振动信号和键相信号;
步骤2:数字跟踪滤波。利用键相信号进行转速计算设置滤波器频率,并截取相邻三个键相信号之间的一段振动信号进行跟踪滤波;
步骤3:等角度时间序列计算。对相邻三个键相点之间的振动数据进行等角度时间序列计算;

图6 计算阶比分析流程图
步骤4:利用样条插值进行幅值拟合,得到等角度序列所对应的幅值序列;
步骤5:对幅值加汉宁窗,在角域进行FFT变换。
3 验证及分析
3.1 验证跟踪滤波的作用
Matlab仿真一个模拟信号:

该信号包含1阶、3阶、12阶成分。我们关心的最大阶比为Lm=4阶,假设最高转速为Rm= 3 000r/min,由式(3)、(5)可计算出最高截止频率fc=fm=3 000×4/60=200Hz。依式(4),此时对应的采样频率fs=200×2.56=512Hz,为了保证滤除效果,取fs为1 000Hz,通过式(4)反求其对应的截止频率不到400Hz,完全可以滤除仿真信号600Hz的频率成分,所以取fs=1 000Hz。如图7所示600Hz成分及图8的12阶成分被滤掉,没有翻折到别的频率上。

图7 最高转速为3 000r/min滤波后频谱图

图8 最高转速为3 000r/min滤波后阶比图
若最高截止频率fc仍为200Hz,而最高转速变为Rm=300r/min,fs=100Hz时。如图9所示60Hz成分没有被滤掉,而被翻折到40Hz,且图10的12阶成分被翻折到8阶。可见,抗混叠滤波器的截止频率若为固定值,则可能出现虚假的频率成分,造成频率混叠。

图9 最高转速为300r/min时滤波后频谱图

图10 最高转速为300r/min时滤波后阶比图
因此由上述3 000r/min和300r/min的仿真验证可得,抗混叠滤波器的截止频率不能一直固定不变是某个常数,需要进行实时跟踪滤波,并实时根据转速信号来调整抗混叠滤波器的截止频率。将高于分析阶比的信号滤除,避免频率混叠。
3.2 用仿真非平稳信号验证阶比-全息谱法应用效果
用两个频率非平稳的扫频信号模拟某一个截面的两个测点振动信号,模拟信号如式(10)和式(11)所示。X,Y为同一截面上两个互成90°的振动信号。取采样频率为2 048Hz。X,Y方向扫频信号时域图见图11和图12。

图11 X方向扫频信号时域图

图12 Y方向扫频信号时域图

图13 X方向扫频信号频谱图

图14 Y方向扫频信号频谱图
由图13、图14可得X,Y在0~20Hz都有值,频谱图频率模糊,无法确定基频,因此无法画出二维全息谱。所以对X,Y信号进行阶比分析,并作出阶比谱图如图15和图16。

图15 X方向信号阶比谱图

图16 Y方向信号阶比谱图
再用MATLAB软件做二维全息谱图,如图17所示一倍频为一个较大的圆与式(10)、(11)X,Y模拟信号的相位相差90°相符合,其他倍频幅值很小也与模拟信号相符合[13]。

图17 模拟启车X信号的二维全息谱图
由以上仿真模拟可看出,对频率非平稳信号先进行阶比分析再做全息谱分析即可作出其全息谱图,从而能较准确的表达振动特征。
3.3 实验模拟验证
在Bently转子实验台上进行3种情况下转子启车的模拟实验,用DT9837B数据采集卡对转子启车过程进行连续数据采集。采样频率fs= 2 048。其中“○”表示初相点,“*”表示后续的点。
阶比全息瀑布图原理:对转子启车过程某一截面X、Y两个方向的振动信号通过计算阶比跟踪提取主要阶次分量,并求取各转速下幅值和相位,将两个方向的各阶振动分别结合起来绘制出各阶的全息谱图,按照转速排列得到阶比-全息瀑布图,可以直观地看出启车过程中各阶全息椭圆的大小、初相点、偏心率、倾角等在不同转速下的变化情况,获得更为丰富的启停车信息。
3.3.1 正常转子升速到7 000转的非平稳状态模拟
Bently转子试验台见图18。图19为正常转子启车的阶比-全息瀑布图,由图19可以看出在1 800r/min和6 000r/min附近时,转子的二维全息谱椭圆向径剧烈变大,初相点翻转了大约180°,整个椭圆也几乎翻转了180°,向径长度剧烈先变大后变小。由此推断,转子在这两个速度下达到了临界转速。另外从图中还可看出,转子的主要振动为一阶工频,其他倍频分量振动很小。由此可以看出,阶比-全息谱方法可以准确的表达转子在启车非平稳状态下的振动特征。

图18 Bently转子试验台
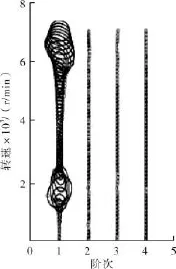
图19 正常转子启车阶比-全息瀑布图
3.3.2 裂纹转子升速非平稳状态模拟
裂纹转子试验台见图20。加工一个裂纹在轴的中部的裂纹转子,裂纹大小约为四分之一的转子直径,在Bently转子实验台进行转子裂纹故障模拟实验,同样用DT9837B采集卡对转子启停机过程进行连续数据采集,取采样频率fs=2 048,绘制其阶比-全息瀑布图见图21。可以看出,转子裂纹故障的主要特征如下:

图20 裂纹转子试验台
1)有较明显的二阶分量;
2)一阶与不平衡相近,在一阶临界转速发生强烈的振动;如果裂纹较深,转子的临界转速会不明确且在一个区域振动比较强烈;
3)临界转速区二维全息谱椭圆翻转比较缓慢;
4)二倍频在1/2临界转速1 000r/min附近出现椭圆;
5)二倍频椭圆比较扁,几乎退化成直线。
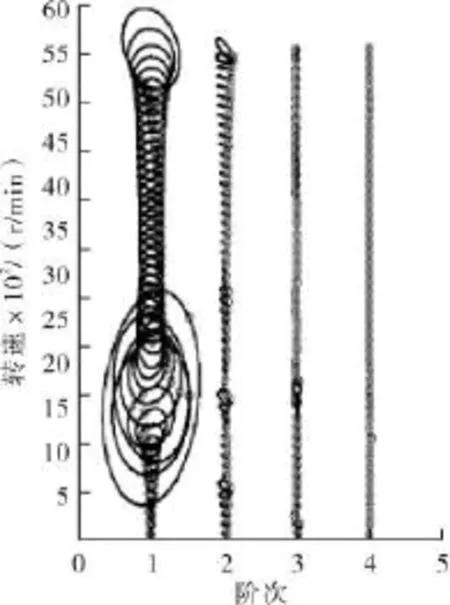
图21 裂纹转子启车阶比-全息瀑布图
由此可知,阶比-全息谱方法可以准确表达裂纹转子在非平稳状态下的振动特征。这对早期的裂纹故障诊断非常重要,因为工业生产中早期的裂纹故障是不容易被我们注意到的,但当裂纹严重到一定程度则会造成事故发生,后果不堪设想。因此转子的裂纹故障不容忽视。
3.3.3 不对中转子升速非平稳状态模拟
不对中转子试验台见图22。不对中是一种常见的机械故障,不对中会导致转子振幅增加、加剧轴承和轴的磨损等。旋转机械多是由多个转子和轴承组成的系统,转子与转子、转子与电机或负载之间用联轴器连接。转子不对中是指两转子的轴心线与轴承中心线的偏离程度。从图23的阶比-全息瀑布图可以看出,转子不对中故障的主要特征如下:

图22 不对中转子试验台
1)1,2阶分量较大;
2)1阶椭圆偏心率较大,由图可看出在2 000r/min附近椭圆相位角发生明显变化;
3)2阶1 000r/min存在亚临界共振,即在转速临界转速的一半时,椭圆比较大;
4)2阶随着转速的变化时大时小。
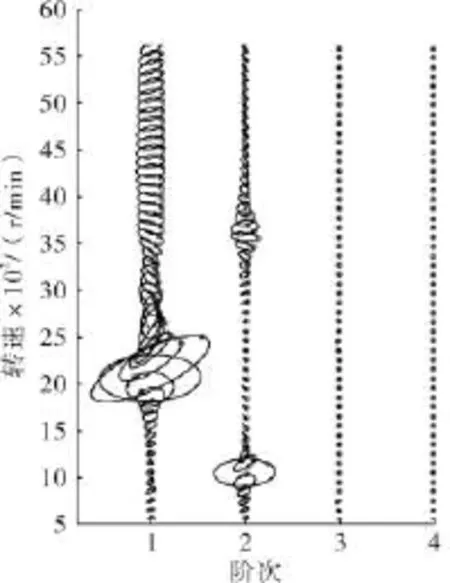
图23 不对中转子启车阶比-全息瀑布图
由此实验可以证明,阶比-全息谱方法可以更为准确的表达转子在不对中非平稳状态下的振动特征。转子不对中可能会造成转子在旋转过程中引发转子的轴绕曲、振动、油膜失稳和轴承损坏等故障,对机械的安全运行造成很大的危害,必须加以高度重视。
以上三种验证试验可以充分说明,阶比-全息谱方法能够更为准确的表达转子在各种非平稳状态下的振动特征,对于诊断转子在非平稳状态下的一系列故障有着极其重要的意义。
4 结论
对于旋转机械在非平稳情况下的转子运行状态,用传统的频谱分析进行故障特征提取研究可能会造成频率混叠等问题,采用将计算阶比分析和全息谱技术相结合的阶比-全息谱方法,通过仿真信号和试验台模拟非平稳信号分析结果表明:该方法能够实现非平稳状态下旋转机械故障特征信息的准确提取,可以更为准确地分析诊断其故障诊断原因,进而对旋转机械的平稳安全可靠性运行提供有力的理论支撑与技术保障。本文虽对部分旋转机械故障进行了分析和诊断,但对种类繁多的旋转机械故障及每种故障定量分析还需要深入研究。
[1]陆春月,王俊元.机械故障诊断的现状与发展趋势[J].机械管理开发,2005(6):85-86.
[2]屈梁生.机械故障的全息诊断原理[M].北京:科学出版社,2007.
[3]何正嘉,訾艳阳,张西宁.现代信号处理及工程应用[M].西安:西安交通大学出版社,2007.
[4]赵国利,齐俊梅,任涛,等.状态监测技术在BCL506离心压缩机故障诊断上的应用[J].风机技术,2011(4):79-82.
[5]尚恩清,董友.离心压缩机的振动分析及解决措施[J].风机技术,2011(4):69-72.
[6]屈梁生,史东锋.全息谱十年:回顾与展望[J].振动测试与诊断,1998,18(4):235-242,303.
[7]温广瑞,李扬,廖与禾,等.基于精确信息重构的故障转子系统振动加速度信号积分方法[J].机械工程学报,2013,49(8):1-9.
[8]赵晓平,张令弥,郭勤涛.旋转机械阶比跟踪技术研究进展综述[J].地震工程与工程振动,2008(6):213-219
[9]宋文健.阶比分析方法的研究[D].秦皇岛:燕山大学,2006.
[10]Fyfe KR,Munck EDS.Analysis of computed order tracking[J]. Mechanical Systems and Signal Processing,1997,11(2): 187-205.
[11]Bossley KM,McKendrick RJ,Harris CJ,etal.Hybrid computed order tracking[J].Mechanical Systems and Signal Processing, 1999,13(4):627-641.
[12]吴剑,孙秀霞,李士波.基于样条插值的计算阶比分析方法[J].弹箭与制导学报,2006(3):211-213.
[13]徐敏强,张嘉钟.基于MATLAB软件平台的全息谱图及在风机振动故障诊断中应用的研究[J].风机技术,2000(2): 38-41.
Research on Calculation of Order Analysis and Holospectrum of Non-stationary Signal Methods for Rotor
Ni Yuchen/Haiyuan Measure and Control Technology Co.,Ltd,The 705 Research Institute,China Shipbuilding Industry Corporation;
Liao Yuhe,Ma Zaichao,Liu Qingcheng/ School of Mechanical Engineering,Xi’an Jiaotong University
For the rotor frequency under the condition of non-stationary signal is difficult to adopt by traditional spectrum analysis method to extract the frequency characteristics.A new method based on order analysis and holospectrum technique is put forward.Calculation order analysis is used to equal angle sampling of frequency modulation signal,and to extract the demand order.Holographic spectrum is used to express amplitude variation.The normal rotor signal,crack rotor signal,and misalignment rotor signal is experimentally simulated.The result showed that this method can realize the fault feature extraction under non-stationary condition and can provide a reference and basis for actual production site in monitoring,fault diagnosisand assessment.
order analysis;holospectrum; equal angle sampling;rotor;fault feature extraction
TH113;TK05
A
1006-8155(2015)04-0019-09
10.16492/j.fjjs.2015.04.012
2015-01-15陕西西安710075

