运行工况传递路径分析方法研究进展

卢英英 成玮 陆建涛 张周锁

摘要：分析了近年來传统TPA（transfer path analysis，TPA）、运行工况TPA（operational TPA，OTPA）、OPAX（operational-X TPA）以及混合TPA方法的基本原理、优势和不足以及工程应用，阐述了功率流法在TPA领域的潜在应用；重点针对OTPA方法，考虑了参考点距离的影响，设计了辐射球声源声传递路径仿真系统和激振器激励矩形板振动传递路径实验系统。结果表明：OTPA值与理论值和实验值的相对误差分别小于5%和8%，与此同时，OTPA方法对噪声很敏感，当噪声较小时，较近参考点有利于提高OTPA方法的精度，因此，应合理布置传感器和设计运行工况；最后，对TPA方法的发展趋势进行了展望。

关键词：机械动力学与振动；运行工况传递路径分析；功率流；声传递路径仿真系统；振动传递路径实验系统

中图分类号：TB533文献标志码：A

Research progress of operational transfer path analysis method

LU Yingying1， CHENG Wei1，2， LU Jiantao1， ZHANG Zhousuo1，2

（1.School of Mechanical Engineering， Xian Jiaotong University， Xian， Shaanxi 710049， China；2.State Key Laboratory for Manufacturing System Engineering， Xian Jiaotong University， Xian， Shaanxi 710049， China）

Abstract： Firstly， the basic principles， the advantages， the disadvantages and the engineering applications of the conventional TPA， OTPA， OPAX and mixed TPA in recent years are comprehensively analyzed. Meanwhile， the potential applications of power flow in the TPA field are especially discussed. Secondly， focused on the OTPA method， an acoustic transfer path system by spherical radiation transfer path simulation system and a vibration transfer path experiment system by a rectangular plate vibrator excitation are designed considering the effects of the distance from reference points. The results show that the relative error between the OTPA values and the theoretical values as well as the experimental values is less than 5% and 8% respectively. At the same time， OTPA is sensitive to noise. When the noise is lower， the nearer reference points can improve the precision of OTPA method. Therefore， it is needed to arrange sensors and design operating conditions reasonably. Finally， the development trend of TPA method is presented.

Keywords：machine dynamics and vibration； operational transfer path analysis （OTPA）； power flow； acoustics transfer path simulation system； vibration transfer path experiment system

收稿日期：2015-02-11；修回日期：2015-03-28；责任编辑：李穆

基金项目：国家自然科学基金（51305329）；高等学校博士学科点专项科研基金（20130201120040）；中国博士后科学基金（2013M532032，2014T70911）；陕西省博士后基金

作者简介：卢英英（1989—），女，甘肃庆阳人，硕士研究生，主要从事运行工况传递路径分析方法等方面的研究。

通讯作者：成玮博士。E-mail：chengw@mail.xjtu.edu.cn

卢英英，成玮，陆建涛，等.运行工况传递路径分析方法研究进展[J].河北科技大学学报，2015，36（4）：359-367.

LU Yingying， CHENG Wei， LU Jiantao，et al.Research progress of operational transfer path analysis method[J].Journal of Hebei University of Science and Technology，2015，36（4）：359-367.随着人们生活质量的不断提高，科技的飞速发展，轿车和高速列车成为人们日常生活中不可缺少的交通工具。振动、噪声和声振粗糙度的性能是评价车辆乘车舒适度的重要指标[1]。水下航行器的声隐身性是衡量其安全性和作战性的重要指标[2]，在低、中速航行时，机械设备的振动是其辐射噪声的主要来源[3]。

车辆和船舶等复杂机械系统包括大量零部件，每个响应点的振动和噪声产生于多个激励源经过一系列结构或空气传播路径的混合叠加。为了有效控制振动和噪声，一方面利用机械系统观测混合信号，通过不同信号处理方法[4-7]从混合信号中分离和识别定位主要振动噪声源。另一方面通过分析机械系统振动噪声传递路径的能量辨识主要振动源和噪声源。TPA是基于试验和线性叠加原理的一种能量传播途径识别方法。通过计算各传递路径的能量贡献量，对各传递路径进行排序，研究机械系统的振动噪声传递特性。针对轿车、高速列车的乘坐舒适性以及水下航行器的声隐身性问题，TPA为其结构优化和减振降噪措施提供依据。因此，TPA方法研究有重要的工程应用价值。由于“主动端-路径-被动端”模型[8]的提出，TPA方法被广泛应用于车辆和船舶等机械系统振动噪声源的识别及其贡献量的确定，为其减振降噪措施的正确实施以及声学系统的优化设计提供科学依据。

河北科技大学学报2015年第4期卢英英，等：运行工况传递路径分析方法研究进展 在民用和军用领域，TPA方法具有重要的工程应用价值。本文首先详细分析了近几年来国内外TPA方法的理论研究和发展现状，并引入功率流方法。简单快捷的OTPA方法在实际工程应用中获得广泛关注，但是存在很多问题，综述了弥补其不足之处的方法。其次通过奇异值分解和主分量分析方法对OTPA进行了数值仿真和试验研究，结果表明，OTPA能准确识别主要声振传递路径。最后对TPA方法的研究前景进行了展望，为其进一步的研究和工程应用提供参考。

1TPA方法基本原理

1.1传统TPA

传统TPA[9-11]理论如下：

Ym（ω）=∑Nn=1Hmn（ω）Xn（ω）。（1）

式中：Ym（ω）为被动端点m的总响应；Hmn（ω）为被动端点m与主动端点n的频响函数；Xn（ω）为主动端点n的载荷。由式（1）可知，传统TPA研究2个方面：频响函数测量和载荷识别。

1.1.1频响函数测量

当力锤或激振器不能直接用于频响函数测量时，必须拆除机械系统的主动端和被动端。频响函数的测量方法为直接法和互易法[12]。

直接法：激励主动端，测量被动端的响应，结构传递通过力锤或激振器激励，空气传递通过体积声源激励；

互易法：激励被动端，测量主动端的响应，主要用于结构-声频响函数和声-声频响函数测量。

互易法的实现如下。

1）结构-声频响函数[13-14]

结构-声频响函数描述振动量与声学量的关系，将体积声源放置在被动端，加速度传感器安放在主动端，通过布置一定数量的传感器，获得全部主动端-被动端的频响函数。结构-声频响函数如式（2）所示：

Hmn（ω）=Pm（ω）/Fn（ω）=V（ω）/Qn（ω），（2）

式中：V（ω）为结构表面振动速度；Qn（ω）为麦克风位置处的体积速度；Hmn（ω）为被动端点m和主动端点n的结构-声频响函数。由于结构振动分布在低频段，为保证结构-声频响函数的精度，体积声源需满足以下条件：

①体积声源近似点源；

②体积声源能够形成高幅值低频信号，使结构表面的传感器输出良好的加速度值；

③精确测量体积速度。

2）声-声频响函数[15]

空气传递揭示声-声频响函数，测量过程如下：被动端安放体积声源，噪声源附近安装麦克风。由于空气噪声分布在中高频段，不要求体积声源高幅值低频特性。声-声频响函数如式（3）所示：

Hmn（ω）=Pm（ω）Qn（ω），（3）

式中：Hmn（ω）为噪声源n和被动端点m的声-声频响函数；Pm（ω）为被动端点m的声压；Qn（ω）为噪声源n的體积速度。

1.1.2载荷识别

TPA是否准确也取决于载荷识别的精度，载荷分为结构载荷和声学载荷。

1） 结构载荷

结构载荷识别方法有直接测量法、悬置刚度法和逆矩阵法。

①直接测量法：直接通过力传感器测量工作载荷，但需要一定的空间和面积，工程应用中的机械系统不满足这些条件。

②悬置刚度法：主动端和被动端由弹性元件连接时，通过弹性元件两端的振动位移差值与弹性元件动刚度的乘积识别工作载荷。

③逆矩阵法：被动端响应乘以相应的频响函数矩阵的广义逆识别工作载荷。通过最小二乘法、奇异值分解和正则化[16-17]抑制频响函数矩阵广义逆的病态问题。

2）声学载荷

声学载荷识别方法有3种，分别为点到点表面采样法、声强测量法和逆矩阵法。

①点到点表面采样法：根据辐射表面加速度乘以表面积得到等效激励源的体积加速度。

②声强测量法：稳态工况下，在消声室测量声源声强，估计声源的声功率，根据声功率计算声源的体积速度。

③逆矩阵法：根据被动端的响应声压，通过声压与体积速度频响函数矩阵的广义逆求得工作体积速度。

3）3种声学载荷识别方法的使用场合

点到点表面采样法常用来确定板振动的传递路径[18]；声强测量法适合复杂的辐射表面，在中高频段，可以得到较好的结果，但局限于消声室和稳态工况；逆矩阵法不受工况限制，适合于现场测量，但需要测量大量频响函数。

频响函数和工作载荷的精度是传统TPA的2个关键点。目前中国占据重要角色的TPA是传统TPA方法。2012年—2014年，侯锁军、张磊、鲍玉军等[1，19-22]通过传统TPA方法分别成功识别出轿车动力总成悬振动的主要传递路径，建立了准确的双层圆柱壳体水下振动-声辐射模型和辨识出高速动车组的主要噪声源等。其中，张磊等首次运用互谱技术、平均技术、加窗技术以及正则化技术求解频响函数矩阵，鲍玉军等将传统TPA方法的应用范围从轿车推广到高速动车组。

传统TPA准确度高，理论完善，但是主动端与被动端的分离改变机械系统边界条件，延长建模时间，适合较简单的机械系统。不同信号处理方法与传统TPA方法的融合是传统TPA方法今后的重点研究方向。

1.2OTPA

传统TPA分离机械系统主动端和被动端，破坏机械系统边界条件，频响函数测试量大。为克服传统TPA的缺点，OTPA被提出[23-27]。OTPA与传统TPA本质区别是传递函数不同，前者是基于力-响应的频响函数矩阵测试，后者是基于响应-响应的传递率矩阵计算。OTPA模型如式（4）所示：

y11（ω）…yn1（ω）

y1r（ω）…ynr（ω）=x11（ω）…xm1（ω）

x1r（ω）…xmr（ω）×T11（ω）…T1n（ω）

Tm1（ω）…Tmn（ω），（4）

式中：ynr（ω）为被动端工况r时响应点n的振动响应；xmr（ω）为主动端工况r时响应点m的振动响应：Tmn（ω）为被动端响应点n与主动端响应点m的传递率。

对比式（1）和式（4），OTPA与传统TPA的表达形式几乎相同，但是OTPA是基于响应-响应的传递率矩阵计算，而传统的TPA是基于力-响应的频响函数矩阵测量，可将式（4）简化为式（5）：

Y=XT。（5）

由式（5）可知，运用OTPA进行声振传递路径分析面临如下关键问题：

1）系统模态使主动端某点的激励在被动端某点及其他路径的输入点引起响应，从而导致传递路径相互串扰；

2） 传递率矩阵计算要求不同工况的响应不相关，实际数据的相关性影响传递率矩阵的精度；

3） OTPA是基于传递率的TPA方法，不同于传统TPA的频响函数，OTPA不能描述机械系统的模态频率和模态振型，因此OTPA无法识别没有被激发模态的传播途径，从而丢失路径。

针对以上问题，奇异值分解和主分量分析被广泛应用于OTPA，在一定程度上保证了OTPA的精度。2013年，袁旻忞等[28]通过奇异值分解和主分量分析，运用OTPA识别出高速列车CRH380B车厢内的噪声源；2014年，伍先俊等[29]应用奇异值分解，通过OTPA成功给出某汽车噪声源排序。

为了弥补OTPA的缺陷，2011年王彬星等[30]针对中高频传递率函数的相位差异，提出运行工况下的能量传递路径分析（operational energy TPA，OETPA），通过试验验证其稳定性；2012年，张磊等[3]针对主动端和被动端的响应同时存在测量噪声现象，应用基于奇异值分解的截断总体最小二乘方法建图1基于奇异值分解的OTPA算法流程

Fig.1Algorithm flowchart of OTPA based on

singular value decomposition

图2OPAX示意图

Fig.2Sketch of OPAX立了有效的水下圆柱壳体结构的OTPA模型；2013年，曹跃云等[31]针对振源耦合较强的船舶结构，借鉴盲源分离方法优点，提出耦合振动噪声源分离方法，建立了准确的船舶OTPA模型；2013年，张磊等[2]针对舰船结构复杂，通过隔振器两端位移差消除源交叉耦合、通过基于奇异值分解的截断总体最小二乘方法抑制传递率矩阵病态、通过基于偏相干理论建立的重相干系数避免路径遗漏，建立了准确、高效的舰船振动-声OTPA模型。

基于以上分析，目前OTPA方法在实际工程中得到了广泛应用。基于奇异值分解和主分量分析的OTPA建模步骤，通过式（5）获得传递率矩阵，由于工况数据的相关性和测量噪声，工况数据直接求逆会出现严重病态问题。首先对工况数据进行奇异值分解和主分量分析见式（6），减小工况数据的相关性、降低测量噪声、减轻模型病态程度；其次求解传递率矩阵见式（7）；最后进行声振传递路径分析。

X=UΣVT，（6）

T=VΣ-1UTY。 （7）

基于奇异值分解的OTPA算法流程如图1所示，关键技术是降低源串扰、数据相关和噪声，减轻伪逆病态程度，获得高精度传递率矩阵。与传统TPA相比，OTPA建模时间短，通过工况数据求得传递率矩阵，一方面避免测量大量的频响函数；另一方面不分离系统主动端和被动端，保持机械系统边界条件不变。

快速有效的OTPA方法适合船舶、车辆等较复杂机械系统的声振传递路径分析，运用不同的信号处理方法可以提高OTPA的精度。

1.3OPAX

为克服OTPA存在的问题，提出OPAX（operati-onal-X TPA）方法[32]，其基本思路：以工况数据为主，以少量的频响函数测量为辅。OPAX的关键是使用参数模型识別工作载荷，具有一定的伸缩性。如图2所示，OPAX引入显示点，显示点和目标点的响应分别满足式（8）和式（9），结构载荷如式（10）所示：

uq（ω）=∑ni=1Hqi（ω）Fi（p，aai（ω），api（ω）），（8）

yk（ω）=∑ni=1Hki（ω）Fi（p，aai（ω），api（ω）），（9）

Fi（ω）=f（p，aai（ω），api（ω）），（10）

式中：Hki（ω）为结构载荷到目标点的频响函数；Hqi（ω）为结构载荷到显示点的频响函数；yk（ω）为第k个目标点总响应；uq（ω）为第q个显示点总响应；aai（ω）为第i个连接处主动端振动响应；api（ω）为第i个连接处被动端振动响应；Fi（ω）为第i个连接处的结构载荷。

与传统TPA相同的是频响函数测试，由于显示点的数量少于传统TPA参考点的数量，OPAX频响函数的测试时间较短；不同的是OPAX通过参数化模型悬置刚度法识别结构载荷。OPAX应用工况数据，引入显示点，显示点数量影响OPAX的复杂程度和精度，参数化载荷识别的2种模型如下。

1）单自由度模型（SDOF）

对于具有单自由度特性的弹性元件连接系统，结构载荷可以通过式（11）得到：

Fi（ω）=Ki（ω）（aai（ω）-api（ω））-ω2，（11）

Ki（ω）=-miω2+jciω+ki，（12）

式中：mi为动刚度；ci为阻尼；ki为弹性元件的静刚度；Ki（ω）为动刚度。

2）多级带宽模型（MB）

当系统不满足SDOF条件时，可使用多级带宽模型，动刚度如式（13）所示：

Ki（ω）=ki，（13）

式中：ki为第i频段内的等效常数刚度。

根据以上分析，OPAX具有传统TPA的高精度，OTPA的高效率。OPAX的关键是参数化载荷识别，为了验证OPAX模型的准确性，必须进行动刚度试验。OPAX适合于客车等复杂机械系统。2013年，周鋐等[33]运用OPAX方法成功识别出某客车主要结构传递路径。

1.4混合TPA

传统TPA，OTPA和OPAX均依赖试验数据，测量误差影响传递路径分析的精度。随着有限元技术的不断发展，以及在实际工程中的广泛应用，混合TPA方法，可以通过试验和数值仿真模型相结合，获得TPA模型中的载荷和频响函数数据。混合TPA一方面减少了试验工作量、节省时间，另一方面避免测量误差的影响，保证精度[34]。

1.5功率流法

上述4种方法都是以传统TPA理论为基础，对复杂结构（比如多级隔振系统等）进行传递路径分析时，“频响函数”不能全面反应传递能量的分布。

传递路径可以表示为能量的传播方向，是力与运动的相互作用。振动功率流描述为力与速度的乘积，反映振动能量，揭示能量传递路径、变化和衰减规律。因此，功率流法可以识别主要传递路径[35-37]。基于不同的机械系统动力特性研究分析方法，将功率流法分为以下5种。

1.5.1统计能量分析法

统计能量分析法[38]是通过统计方法，从能量的角度研究振动和噪声问题，用统计参数表示系统，以此得到子系统的能量分布，其主要用于高频分析，中低频分析误差较大。统计能量分析法可以准确计算整体的平均响应，但对局部响应的预测可信度较低。

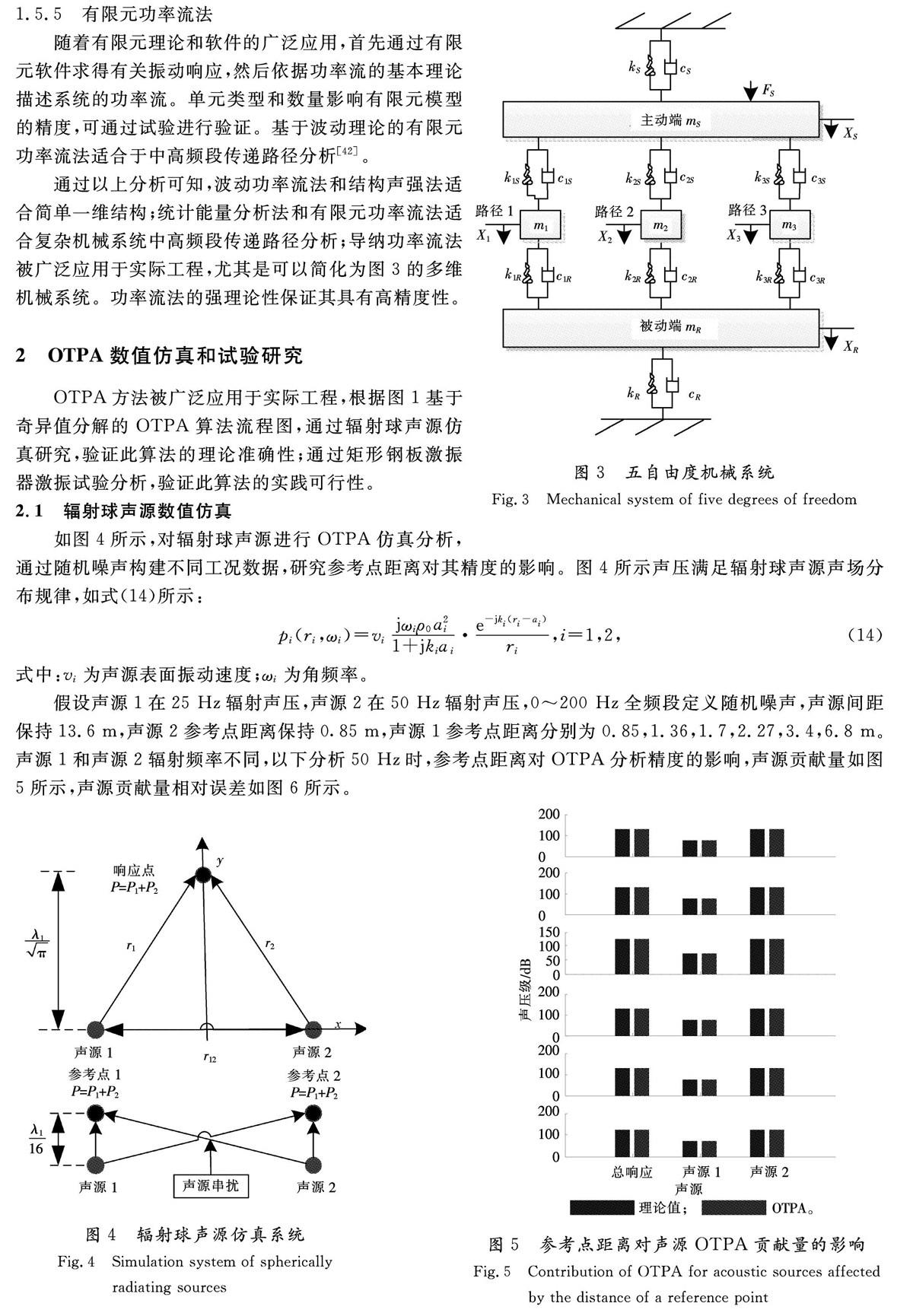
图3五自由度机械系统

Fig.3Mechanical system of five degrees of freedom

1.5.2波动功率流法

将波动法引入振动能量分析，主要用于杆、梁等一维结构或周期结构能量传递研究。波动功率流法[39]可以描述整体和局部能量分布以及功率流传递路径。但不适合复杂结构。

1.5.3结构声强法

结构声强法是将空气声学的声强理论引入到固体力学，描述单位截面内的功率流[40]。同于波动功率流法，结构声强法适合于简单的杆、梁、薄膜、板等结构。

1.5.4导纳功率流法

导纳功率流法依赖结构的导纳特性[41]。机械系统的导纳表示为系统的输出和输入之比，利用导纳可以描述组合结构的传递特性，如图3所示。依据导纳分析的前后顺序，将系统划分为具有导纳特性的相互串联或者并联的子系统，以导纳表示各个子系统的能量输入输出关系，借助传递规律求得传递路径。

1.5.5有限元功率流法

随着有限元理论和软件的广泛应用，首先通过有限元软件求得有关振动响应，然后依据功率流的基本理论描述系统的功率流。单元类型和数量影响有限元模型的精度，可通过试验进行验证。基于波动理论的有限元功率流法适合于中高频段传递路径分析[42]。

通过以上分析可知，波动功率流法和结构声强法适合简单一维结构；统计能量分析法和有限元功率流法适合复杂机械系统中高频段传递路径分析；导纳功率流法被广泛应用于实际工程，尤其是可以简化为图3的多维机械系统。功率流法的强理论性保证其具有高精度性。

2OTPA数值仿真和试验研究

OTPA方法被广泛应用于实际工程，根据图1基于奇异值分解的OTPA算法流程图，通过辐射球声源仿真研究，验证此算法的理论准确性；通过矩形钢板激振器激振试验分析，验证此算法的实践可行性。

2.1辐射球声源数值仿真

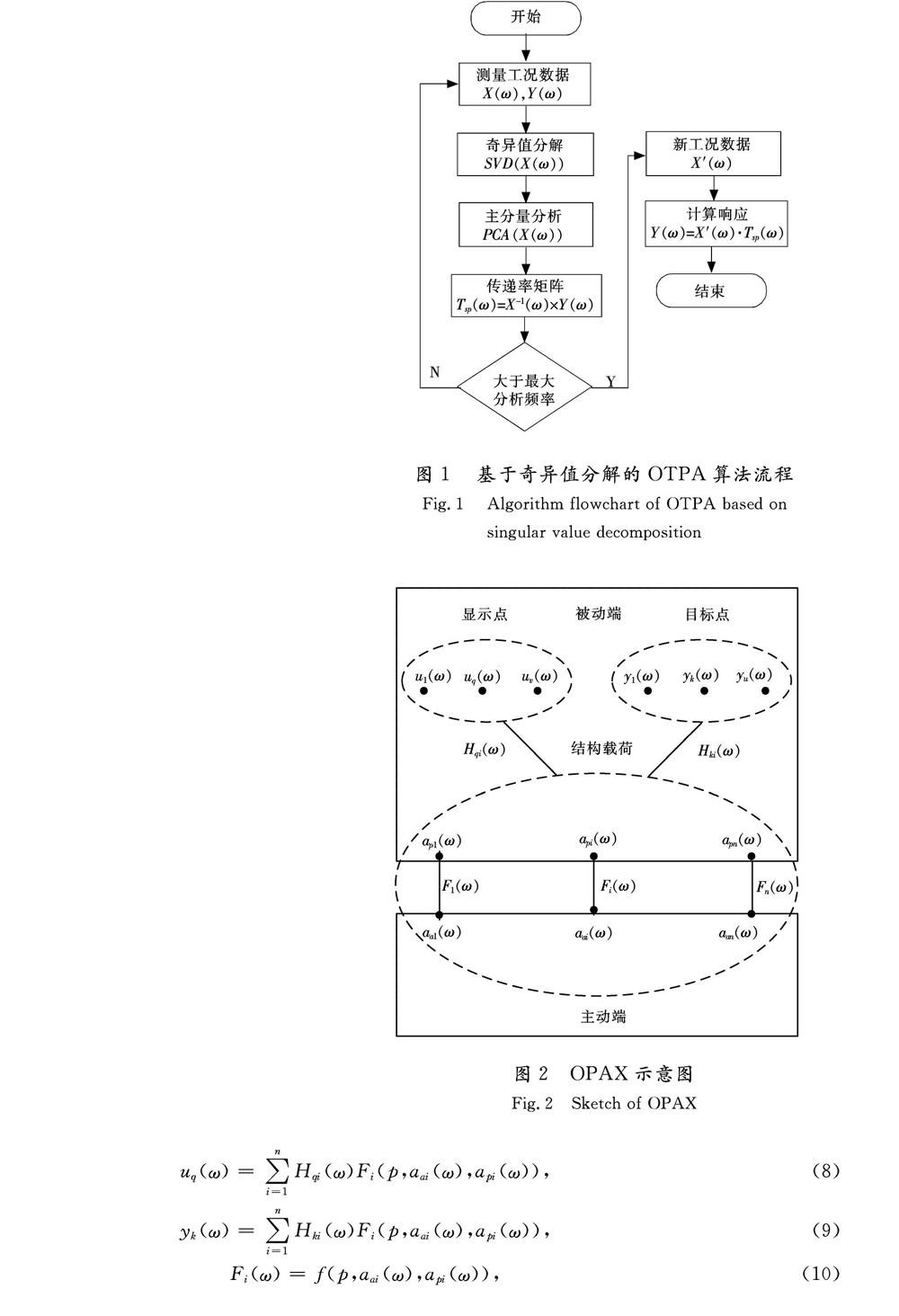
如图4所示，对辐射球声源进行OTPA仿真分析，通过随机噪声构建不同工况数据，研究参考点距离对其精度的影响。图4所示声压满足辐射球声源声场分布规律，如式（14）所示：

pi（ri，ωi）=vijωiρ0a2i1+jkiai·e-jki（ri-ai）ri，i=1，2，（14）

式中：vi为声源表面振动速度；ωi为角频率。

假设声源1在25 Hz輻射声压，声源2在50 Hz辐射声压，0～200 Hz全频段定义随机噪声，声源间距保持13.6 m，声源2参考点距离保持085 m，声源1参考点距离分别为0.85，1.36，1.7，2.27，3.4，6.8 m。声源1和声源2辐射频率不同，以下分析50 Hz时，参考点距离对OTPA分析精度的影响，声源贡献量如图5所示，声源贡献量相对误差如图6所示。

图4辐射球声源仿真系统

Fig.4Simulation system of spherically

radiating sources图5参考点距离对声源OTPA贡献量的影响

Fig.5Contribution of OTPA for acoustic sources affected

by the distance of a reference point

图6参考点距离对声源OTPA精度的影响

Fig.6Precision of OTPA for acoustic sources affected

by the distance of a reference point 图5表明，50 Hz时，声源2辐射声压，由于随机噪声存在，理论和OTPA均出现伪声源1。图6表明，随机噪声导致OTPA对参考点距离的变化很敏感。图5和图6表明，50 Hz时，声源2对应主要声传递路径；参考点距离对OTPA总响应和声源贡献量影响很小，并且OTPA与理论值误差均小于5%；较大的参考点距离有利于减小随机噪声对OTPA精度的影响。

2.2矩形钢板试验研究

在辐射球声源声传递路径分析中，随机噪声可实现不同工况。以下通过改变激振器输出信号构造不同工况，研究参考点距离对OTPA精度的影响，验证OTPA算法的实践可行性。激振器激励试验装置如图7所示，不同工况如表1所示，通过表1的工况获得传递率矩阵，应用此传递率矩阵进行新工况的振动传递路径分析。

图7矩形钢板激振器激励试验示意图

Fig.7Sketch of the experiment for a rectangular

plate excited by vibrators

表1不同工况信号

Tab.1Signal of various working conditions

工况振动源1振动源21sinc正弦2锯齿正弦3冲击正弦4白噪声正弦

假设振动源1输出25 Hz方波，振动源2输出50 Hz正弦波，振动源间距为31.62 cm，参考点距离分别为2.83 cm和5.66 cm，分析25 Hz时，参考点距离对OTPA精度的影响，振动源1贡献量及其误差如图8和图9所示。图8表明，25 Hz时，振动源1对应主要振动传递路径；图9表明，随振动源参考点距离增大，OTPA总响应误差和源贡献量误差略有增大，并且均小于8%；试验与仿真分析吻合很好。

图8参考点距离对振动源OTPA贡献量的影响

Fig.8Contribution of OTPA for vibration sources

affected by the distance of a reference point

图9参考点距离对振动源OTPA精度的影响

Fig.9Precision of OTPA for vibration sources

affected by the distance of a reference point

通过仿真和试验分析，OTPA对工况数据很敏感，质量较差的試验数据会导致OTPA结果不可靠。在实际工程中，应合理布置传感器，选择合理的工况组合。

3结语

1） 系统总结了TPA方法，其区别是将功率流方法归纳为TPA方法。在工程应用中，为根据不同实际情况选择不同传递路径方法提供理论依据。

2） 通过随机噪声构造辐射球声源的不同工况，研究参考点距离对OTPA精度的影响，并通过激振器输出不同信号，试验验证了OTPA算法的准确性。仿真和试验结果的一致性表明OTPA可用于声振传递路径分析。在工程应用中，参考点距离应较小。

3） 不同信号分析和处理方法与TPA方法的融合是TPA的研究方向。通过频响函数的无偏估计、载荷识别的正则化等提高传统TPA的精度，通过传递率矩阵的正则化、非线性盲源分离等保证OTPA的准确度。

4） 混合TPA是今后TPA方法的研究热点。建立准确的复杂结构有限元模型，通过仿真模型与试验模型相结合，借助LMS Test.Lab或者LMS Virtual.Lab Acoustic的TPA模块，识别声振传播途径。

参考文献/References：

[1]侯锁军， 史文库， 毛阳. 应用传递路径分析方法对方向盘抖动贡献量的研究[J]. 西安交通大学学报， 2013， 47（3）： 133-136.

HOU Suojun， SHI Wenku， MAO Yang. Vehicle steering wheel wobbling contribution investigation by transfer path analysis [J]. Journal of Xian Jiaotong University， 2013， 47（3）：133-136.

[2]张磊，曹跃云，杨自春，等.运行工况下舰船振动-声传递路径分析及试验[J].华中科技大学学报（自然科学版），2013，41（2）：42-47.

ZHANG Lei， CAO Yueyun， YANG Zichun， et al. Theocratical analysis and experimental validation of vibration-acoustic transferring paths of ships under operational conditions [J]. J Huazhong Univ of Sci & Tech（Natural Science Edition），2013， 41（2）：42-47.

[3]张磊，曹跃云，杨自春，等.水下圆柱壳体结构噪声的工况传递路径分析[J].振动、测试与诊断， 2012， 32（6）： 898-902.

ZHANG Lei， CAO Yueyun， YANG Zichun， et al. Operational transfer path analysis for structural noise of a submerged shell[J].Journal of Vibration，Measurement & Diagnosis， 2012，32（6）：898-902.

[4]成玮，张周锁，何正嘉，等.基于独立分量分析的潜艇振源贡献量定量计算方法[J].机械工程学报， 2010， 46（7）： 83-87.

CHENG Wei， ZHANG Zhousuo， HE Zhengjia， et al. Quantitative calculation of vibration source contributions of submarines based on independent component analysis[J].Journal of Mechanical Engineering，2010， 46（7）：83-87.

[5]李永伟，韩京津，袁涛，等. 基于信息融合的高压电气设备温变故障诊断方法研究[J]. 河北科技大学学报，2012， 33（6）： 501-505.

LI Yongwei， HAN Jingjin， YUAN Tao， et al. Diagnosis of temperature variation fault of high voltage electrical equipment based on information fusion technology[J]. Journal of Hebei University of Science and Technology， 2012， 33（6）： 501-505.

[6] 高志峰，王菊芳，禹长龙，等. 基于T-S模糊建模方法的近空间飞行器姿控系统传感器故障调节技术研究[J]. 河北科技大学学报，2013， 34（6）：552-558.

GAO Zhifeng， WANG Jufang， YU Changlong， et al. Sensor fault accommodation for the attitude control system of near space vehicle based on T-S fuzzy modeling approach[J].Journal of Hebei University of Science and Technology， 2013， 34（6）：552-558.

[7]郭立炜，周昇龙，安国庆，等. 基于中点电压信号分析的逆变器功率管开路故障诊断研究[J]. 河北科技大学学报，2015， 36（1）： 45-51.

GUO Liwei， ZHOU Shenglong， AN Guoqing， et al. Diagnosis of inverter switch open circuit faults based on neutral point voltage signal analysis[J]. Journal of Hebei University of Science and Technology， 2015， 36（1）： 45-51.

[8]GOOSSENS S， OSAWA T， IWAMA A. Quantification of Intake System Noise Using an Experimental Source Transfer Receiver Model[R]. SAE Technical Paper， 1999.

[9]KRUSE A. NVH Improvement of Car Suspension Using Transfer Path and Running Mode Analysis[R]. SAE Technical Paper， 2006.

[10]郭榮， 万钢， 赵艳男， 等. 车内噪声传递路径分析方法探讨[J]. 振动、测试与诊断， 2007， 27（3）： 199-203.

GUO Rong， WANG Gang， ZHAO Yannan， et al. A study on the transfer path analysis method of the interior noise of a car[J].Journal of Vibration， Measurement & Diagnosis， 2007，27（3）：199-203.

[11]LI Wei， WANG Dengfeng， CHEN Shuming， et al. Transfer parth analysis of power train vibration on driver's noise[C]∥Natural Computation （ICNC）， 2011 Seventh International Conference on IEEE.[S.l.]：IEEE， 2011：2353-2357.

[12]SOTTEK R， SELLERBECK P， KLEMENZ M. An Artificial Head Which Speaks from Its Ears： Investigations on Reciprocal Transfer Path Analysis in Vehicles， Using A Binaural Sound Source[R]. SAE Technical Paper， 2003.

[13]GUO R， QIU S， YU Q， et al. Transfer path analysis and control of vehicle structure-borne noise induced by the power train[J].Proceedings of The Institution of Mechanical Engineers， Part D：Journal of Automobile Engineering， 2012， 226（8）： 1100-1109.

[14]ELLIOTT A S， MOOR HOUSE A T，HUNTLEY T， et al. In-auto source path contribution analysis of structure borne road noise[J].Journal of Sound and Vibration，2013，332：6276-6295.

[15]Van Der LINDEN P J G， KEPPENS T， RAFF J， et al. Determination of The Noise Contributions of Engine Surfaces[R]. SAE Technical Paper， 2001.

[16]HOUSEROOM A T. Compensation for discarded singular values in fibro-acoustic inverse methods[J]. Journal of Sound and Vibration， 2003，267：245-252.

[17]YOUNG G C， TITHE N， THOMPSON DAVID J. Comparison of methods for parameter selection in techno regularization with application to inverse force determination[J].Journal of Sound and Vibration， 2007，304：894-917.

[18]劉东明，方健，赵敬义，等.车身板件对车内噪声的贡献量分析[J].噪声与振动控制，2011，31（2）：49-51.

LIU Dongming， FANG Jian， ZHAO Jingyi， et al. Analysis of panel contribution to vehicle interior noise[J].Noise and Vibration Control， 2011，31（2）：49-51.

[19]蒋延国.车辆动力总成传递路径分析[J].机电技术，2014（6）：62-64.

JIANG Yanguo. Transfer path analysis of vehicle power train[J].Mechanical & Electrical Technology， 2014（6）：62-64.

[20]李未，李庆华. 动力总成振动对车内噪声的传递路径影响[J].智能系统学报，2012，7（2）：184-187.

LI Wei， LI Qinghua. Transfer path analysis of power train vibration on automotive interior noise[J].CAAI Transactions on Intelligent Systems， 2012， 7（2）：184-187.

[21]张磊，曹跃云，杨自春，等.双层圆柱壳体水下振动噪声结构传递路径分析[J].振动与冲击，2012，31（20）：13-16.

ZHANG Lei， CAO Yueyun， YANG Zichun， et al. Structural transfer path analysis for vibration and noise of a submerged cylindrical double-shell[J].Journal of Vibration and Shock，2012，31（20）：13-16.

[22]鲍玉军，李聪，杨弘.高速动车组噪声源与传递路径分析[J].铁路技术监督，2014，42（5）：41-45.

BAO Yujun， LI Cong， YANG Hong. Noise sources and transfer path analysis of high speed train[J].Railway Quality Control，2014，42（5）：41-45.

[23]LOHRMANN M， HOHENBERGER T. Operational transfer path analysis： Comparison with conventional methods[J]. Journal of the Acoustical Society of America， 2008， 123（5）： 3534.

[24]GIRT D， CHRIST D， PATRICK G， et al. Operational transfer path analysis[J].Mechanical Systems and Signal Processing， 2010，4（2）：416-431.

[25]DEALER D， OSSEO A.Operational transfer path analysis： Theory， guidelines and tire noise application[J]. Mechanical Systems and Signal Processing，2010，24（7）：1950-1962.

[26]HOSEN N B， LACLEDE Q. On the use of artificial excitation in operational transfer path analysis [J]. Applied Acoustics， 2013， 74：1167-1174.

[27]MAKO R， FERITY K， SEBASTIAN E， et al.Hybrid acoustic synthesis-assessment of rear final drives in an early stage of development， on the basis of transfer path analyses and test bench measurements[J].Applied Acoustics， 2014，80：45-56.

[28]袁旻忞， SHEN Anne， 魯帆，等.高速列车运行工况下噪声传递路径及声源贡献量分析[J].振动与冲击，2013，32（21）：190-195.

YUAN Minmin，SHEN Anne，LU Fan，et al.Operational transfer path analysis and noise sources contribution for china railway high-speed （CRH）[J].Journal of Vibration and Shock，2013，32（21）：190-195.

[29]伍先俊，吕亚东，隋富生.工况传递路径分析法原理及其应用[J].噪声与振动控制，2014，34（1）：29-31.

WU Xianjun， LYU Yadong， SUI Fusheng. Basic theory of operational transfer path analysis and its application[J].Noise and Vibration Control， 2014， 34（1）：29-31.

[30]王彬星，郑四发，郝鹏，等.运行工况下车内噪声的能量传递路径分析[J].噪声与振动控制，2011，31（5）：71-74.

WANG Binxing， ZHENG Sifa， HAO Peng， et al. Operational energy transfer path analysis of vehicle interior noise[J].Noise and Vibration Control， 2011，31（5）：71-74.

[31]曹跃云，张磊，杨自春，等.船舶振动噪声源传递路径分析及试验验证[J].振动与冲击，2013，32（22）：159-162.

CAO Yueyun， ZHANG Lei， YANG Zichun， et al. A new OPA model for ship noise sources and test validation[J]. Journal of Vibration and Shock， 2013， 32（22）：159-162.

[32]KARL H， PETER G， LIDO G， et al. OPAX： A new transfer path analysis method based on parametric load models[J]. Mechanical Systems and Signal Processing， 2011，25（4）：1321-1338.

[33]周鋐，丁慧，吴颖熹，等.新型传递路径分析OPAX方法研究[J].中国工程机械学报，2013，11（5）：386-389.

ZHOU Hong， DING Hui， WU Yingxi， et al. Methodological study on new transfer path analysis[J]. Chinese Journal of Construction Machinery，2013，11（5）：386-389.

[34]PLUNT J. Examples of Using Transfer Path Analysis （TPA） Together with CAE-models to Diagnose and Find Solutions for NVH Problems Late in the Vehicle Development Process[R]. SAE Technical Paper， 2005.

[35]YAM J， LI C F， LI T Y. Vibration power flow analysis of a submerged cisco-elastic cylindrical shell with wave propagation approach[J]. Journal of Sound and Vibration， 2007，303：264-276.

[36]LI C Q. Combination of an improved FRF-based substructure synthesis and power flow method with application to vehicle axle noise analysis[J]. Shock and Vibration， 2008，15：51-60.

[37]YAM J，LI T Y，LI J X， et al. Input power flow in a submerged infinite cylindrical shell with doubly periodic supports [J]. Applied Acoustics， 2008，69：681-690.

[38]柳瑞锋，王强，章艺，等.浮筏隔振系统隔振效果统计能量分析估算方法[J].噪声与振动控制，2010（2）：35-37.

LIU Ruifeng， WANG Qiang， ZHANG Yi， et al. Estimates of vibration isolation efficiency for floating raft isolation system by statistical energy analyzing method [J].Noise and Vibration Control， 2010，30（2）：35-37.

[39]黄迪山，唐亮.机械结构动力学行波法研究进展[J].机械强度，2012，34（6）： 791-797.

HUANG Dishan， TANG Liang. Recent research and development of mechanical structure dynamic study on wave propagation[J].Journal of Mechanical Strength， 2012， 34（6）： 791-797.

[40]曾國英，赵登峰. 动载荷作用下壳体的结构声强分析[J]. 噪声与振动控制， 2010，30（3）：61-62.

ZENG Guoying， ZHAO Dengfeng. Sound intensity analysis of shell structures subjected to dynamic loading[J]. Noise and Vibration Control， 2010，30（3）：61-62.

[41]颜松，盛美萍，陈晓利.多源激励下浮筏隔振系统导纳功率流研究[J]. 噪声与振动控制， 2006，26（4）： 27-28.

YAN Song， SHENG Meiping， CHEN Xiaoli. Mobility power flow analysis for floating raft isolation system [J].Noise and Vibration Control， 2006，26（4）： 27-28.

[42]MACE B R，SHORTER P J. Energy flow models from finite element analysis[J]. Journal of Sound and Vibration， 2000， 233（3）：369-389.第36卷第4期河北科技大学学报Vol.36，No.4