海上拖缆勘探航线优化设计改进及应用

张 虎 刘 丽 宁克岩 胡 斌

（东方地球物理公司 河北涿州 072751）

张虎，刘丽，宁克岩，等.海上拖缆勘探航线优化设计改进及应用［J］.中国海上油气，2015，27（6）：43-47.

施工路径规划是深海拖缆地震采集设计的重要环节之一。与陆上施工相比，海上拖缆勘探具有时间短、成本高的特点，施工路径规划是合理调度和节省时间、降低成本的重要步骤。在理想情况下，设计人员可以直接通过呈现线束条带状的“赛道式”施工方式［1］规划出航线采集路径。但在不规则勘探边界区域、障碍区以及补线等施工时，设计或导航人员自行找到上百条航线最经济、最合理的施工路径是非常困难的。

为解决以上问题，一种固定航向的启发式算法已被应用在设计及施工中，可以达到预测和降低成本的目的［2］，但在实际施工时沿主航向或反航向施工也是常有的。此外，在深海拖缆勘探中，因洋流、潮汐的影响而产生的拖缆羽角现象造成覆盖缺失，还需要在施工中进行补线施工，这样又产生了新的航线和成本。因此，只计算放炮采集段路径和转弯路径的启发式算法［3］得到的结果与实际情况难以匹配，得到的最优施工路径缺乏规律性，不符合传统的拖缆勘探“赛道式”施工方式。

本文同时考虑任意航向（主方向或反方向）和补线成本等因素来建立数学模型，通过模拟退火算法寻找到全局最优解，并以分区线束数作为约束，得到了尽可能与生产更匹配的方案，获得了很好的优化效果。

1 海上拖缆勘探航线优化方法改进

1.1 数学模型建立

在海上拖缆勘探实际施工中，沿主航向或反航向施工是常有的，所以需要考虑2个方向上的航线施工。另外，相邻航线反向施工会产生满覆盖空缺，所以需要在目标函数中考虑补线成本。

如图1所示，一条航线包含2个端点sx和sx′，可以从sx→sx′和sx′→sx两个方向上线施工，所以n条航线2n个点组成序列G=｛s1，s1′，s2，s2′，…，sn，sn′｝。在勘探过程中，为了满足满覆盖边界要求，不同上线方向的航线起止点位置不同，导致序列G上两点之间的距离值也不同：当序列G上的2个点在同一航线时，两点距离为航线长度d（sx，sx′）；当序列G上的2个点不在同一航线时，两点距离为d（sx，sy）、d（sx，sy′）、d（sx′，sy）、d（sx′，sy′）这4种距离之一，利用最小转弯半径的圆弧及其切线组合方法［4］可以分别计算出这4种情况的距离。因此，可以得到n条航线的距离矩阵D为

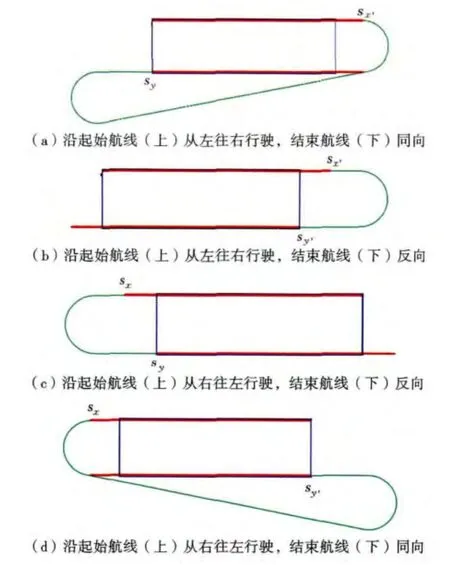
图1 2条航线的4种连接方式Fig.1 Four connection types of two lines

其中

放炮采集段长度与转弯长度之和d（S）为

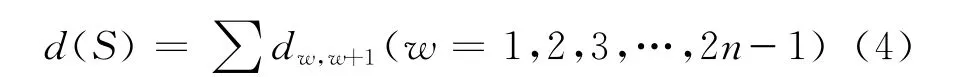
式（4）中：dw，w＋1根据w和w＋1这2个端点所属的航线和方向从距离矩阵D中取值。

补线长度infill（S）为

式（5）中：R为补线因子；L为相邻2条航线的平均长度；m为相邻2条航线反向施工的次数（由程序运算得到）。

总施工长度f（S）为

令f（S）为目标函数，需要求出G=｛s1，s1′，s2，s2′，…，sn，sn′｝的一个排列S=｛sk1，sk′1，sk2，sk′2，…，skn，sk′n｝，使总施工长度f（S）为最小，这里，S中skx、sk′x只能颠倒位置，不能插入其他点。

1.2 最优解求取

模拟退火（Simulated Annealing，SA）算法［5-6］的基本流程是：设定初始温度T0和初始序列S0，伴随温度的不断下降，结合概率突跳特性在解空间中通过邻域函数进行随机搜索，最终得到全局近似最优解，如图2所示。

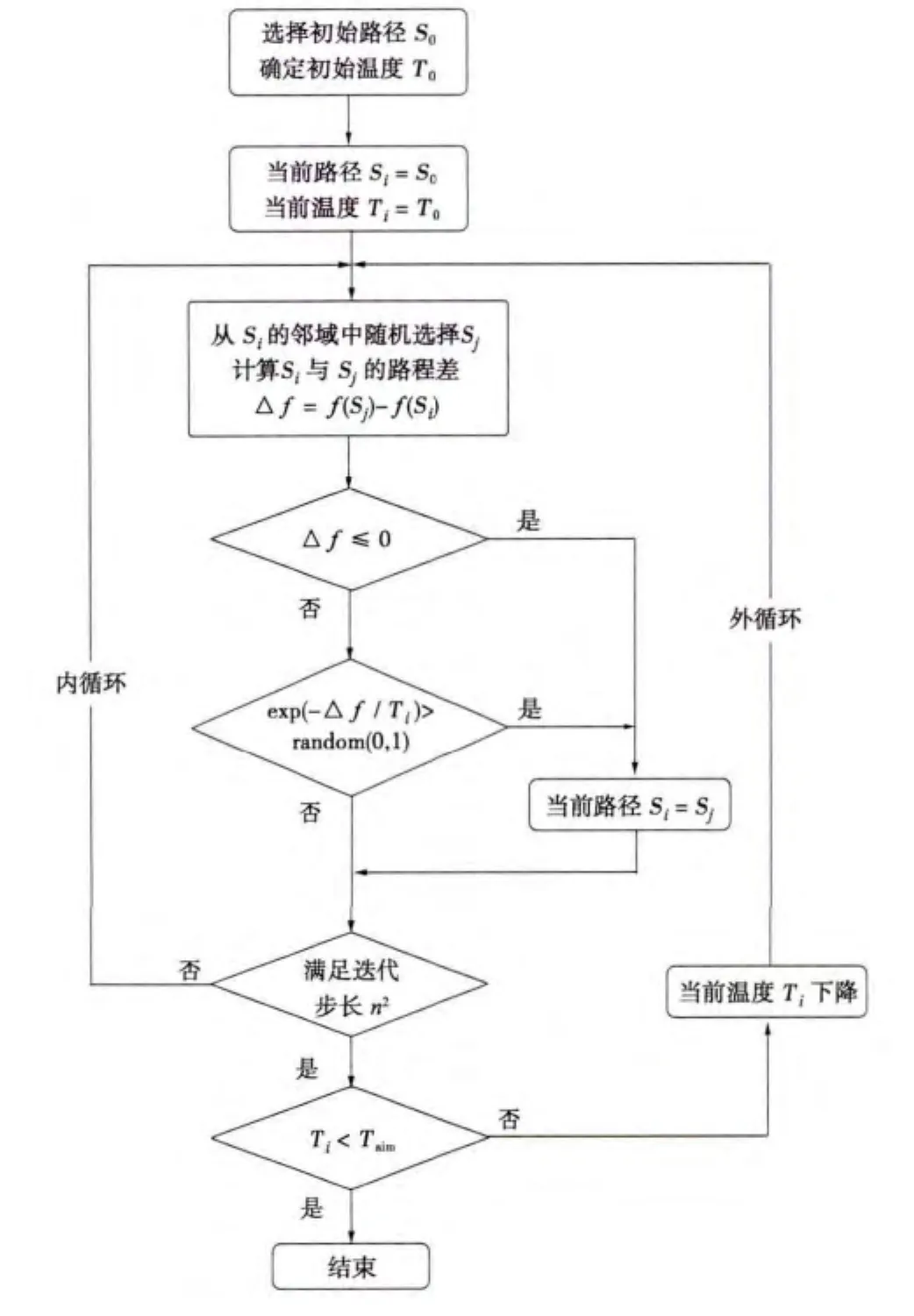
图2 模拟退火算法流程图Fig.2 Flow chart of simulated annealing algorithm

1）初始状态。

设定航线的初始序列为S0，初始路径长度为f（S0），初始温度T0为

式（7）中：Rate为充分大的正数，以保证初始温度T0足够大；n为航线数；dmax是距离矩阵D中的最大值；dmin是距离矩阵D中的最小值。

2）外循环。

外循环是逐步降温的过程，通过温度下降迭代的方式实现外循环，设置终止温度的阈值停止外循环。该降温方式为

式（8）中：K为降温速率。K值越接近1，降温越慢；K值过小，则会使算法陷入局部最优。

在逐步下降的每个温度中进行内循环计算，获得系统当前温度的稳定状态。当温度降到目标温度时，即Ti＜Taim（Taim接近0），外循环完成，模拟退火算法结束。

3）内循环。

内循环是在外循环温度Ti状态下在邻域进行随机搜索的迭代过程。在内循环中，本文采用交换元素的方式产生S的新解S′，在S中随机选择2个元素（航线的端点）并按照规则重新组合关联元素：①当选择的2个元素skx、sk′x在同一航线上，则直接颠倒这条航线的2个端点。②当选择的2个元素不在同一航线上，如果所选元素均为航线的第1个端点skx、sky，保持航线航向不变，只把这2条航线对调；如果 所 选 元 素为sk′x、sk′y，则 先 把 这2条 航 线 对调，再颠倒这2条航线的端点。

交换后的路径距离差为Δd=d（S′）-d（S），实际只计算交换后形成的新边与被变换边的差值。

①2个元素在同一航线上，skx、sk′x初始位置分别为p、p＋1，路径距离差为

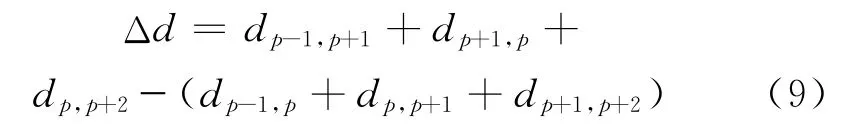
②2个元素 不 在 同 一 航 线 上 ，skx、sk′x、sky、sk′y的初始位置分别为p、p＋1、q、q＋1。当所选元素均为第1个端点时，路径距离差为

当所选元素都为第2个端点时，则按式（10）和式（9）分两步计算Δd。

扫描当前解S′中的相邻航线，得到相邻2条航线反向施工的次数m′，计算出新的补线长度infill（S′）。总长度差为

若Δf≤0，将S′作为新解，即S=S′。反之，通过Metropolis准则计算S′的接受概率exp（-Δf／Ti），并在（0，1）区间上产生随机数random，若exp（-Δf／Ti）＞random，将S′作为新解，即S=S′。当满足规定的迭代步长n2时结束内循环，降温开始下一个外循环。

1.3 R因子对分区线束数的影响

在三维拖缆勘探施工中，除了转弯长度和补线长度外，航线的分区线束数也是合理施工的关键。R因子不仅可以评估航线补线成本，也可以控制航线的分区线束数。因此，通过改变R值可以控制分区线束数得到期待的效果。

1）R=0时，虽然得到全局最优解，但违背实际施工的规律性。

2）引入R值后，路径改进明显，航线集自动分成多个线束。

3）R值越大，反向航线越少，分区线束数越少。但是，当分区线束数减少到不合理的程度时，会产生更多的换线成本。

通过设置不同的R值可以得到多个最优解，形成一个最优解样本。实际生产中，需要同时考虑转弯长度、补线长度和分区线束数等因素，进行综合对比分析，从最优解样本中确定更符合生产环境的一个或多个施工方案。

2 应用实例

以塞拉利昂A工区为例模拟满覆盖布设，该工区满覆盖面积2 848 km2，施工方位角300°，工区内设计153条平行航线，航线间距300 m，转弯半径3 km。本次模拟中每条航线的放炮采集段2个方向的长度是不变的，放炮采集段长度为9 970.625 km（图3中红线）。模拟结果（表1、图3）为：

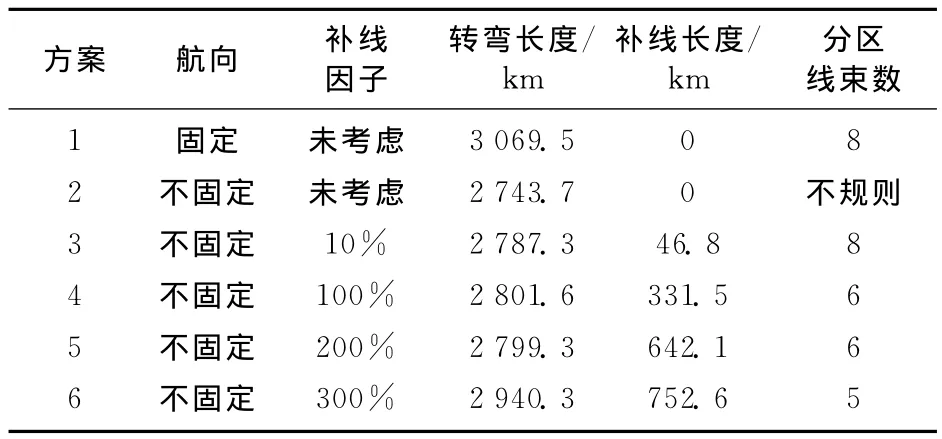
表1 塞拉利昂A工区不同方案模拟结果Table 1 Simulation results of different solutions from A work area in Sierra Leone

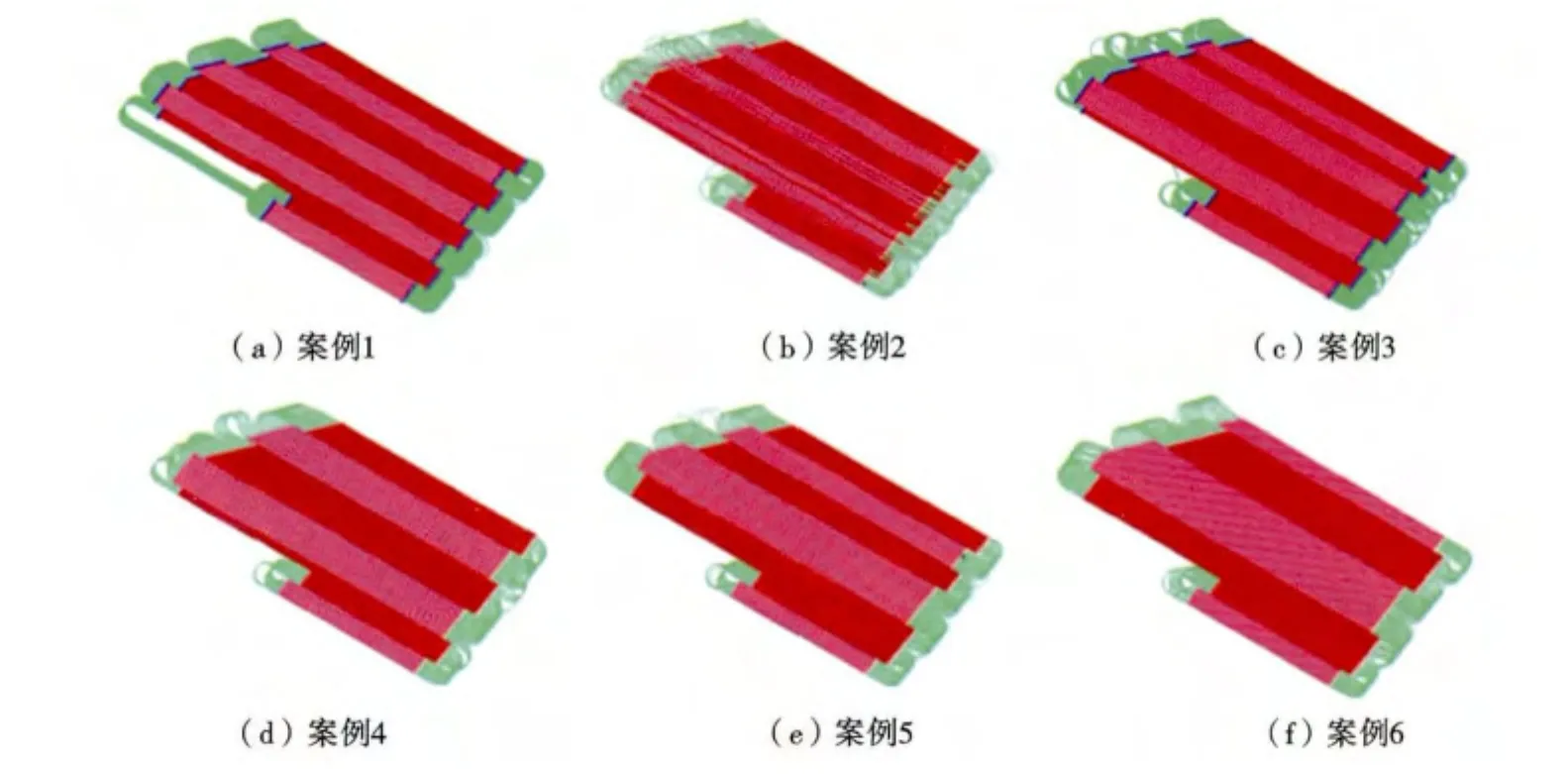
图3 塞拉利昂A工区满覆盖布设模拟效果Fig.3 Simulation results of different full fold layout solutions from A work area in Sierra Leone

1）案例1为初始参考航线集，人工设置为每20条航线取向反转，呈现出较好的分区线束状特性，符合生产的需求，但左侧转弯航线明显不合理，造成较大的转弯成本，转弯长度达3 069.5 km（图3a中绿线）。

2）案例2为不考虑补线成本优化搜索后的结果，转弯长度为2 743.7 km（图3b）。相对于案例1，该方案优化率达到10.6%。虽然案例2的优化率高，但是同时产生了大量相邻航线反向施工，造成巨大的补线成本，因此该方案在实际生产中是不能实施的。

3）案例3中，为了优化出较短的转弯方案以及合理的分区方案，综合考虑补线成本，设置补线因子R=10%，优化搜索后转弯长度减少至2 787.3 km，补线长度为46.8 km，产生8个分区线束块（图3c）。

4）案例4中，增加补线因子至R=100%，优化搜索后转弯长度为2 801.6 km，补线长度为331.5 km。相对于案例3，该方案转弯长度未发生明显改变，但分区线束数由8减少到6（图3d）。由此可见，通过增加R值可以有效减少分区线束数，从而利于采集施工。

5）案例5中，增大补线因子至R=200%，优化搜索后转弯长度为2 799.3 km，补线长度为642.1 km。相对于案例4，虽然补线长度有所增加，但案例5更符合“赛道式”施工方式，也具有更少的“泪滴状”转弯，为最优方案（图3e）。

6）案例6中，增大补线因子至R=300%，优化搜索后转弯长度为2 940.3 km，补线长度为752.6 km。相对于案例4、5，该方案分区线束数减少到5，转弯长度增加了约140 km（图3f），这是因为当分区线束数减少到一定程度时，个别航线转弯跨度变宽，2条线的转弯距离增加。当R值足够大时，方案中将会只有一个线束，显然也不合理。

3 结束语

对海上拖缆勘探航线优化算法进行了改进，同时考虑任意航向和补线成本等因素建立数学模型，通过模拟退火算法寻找到全局最优解，通过设置不同的R值得到多个最优解并形成一个最优解样本，最终以分区线束数作为约束条件，从最优解样本中选取尽可能与生产更匹配的方案。应用实例表明，本文方法能够使海上拖缆勘探施工路径得到明显改善，施工方案更具合理性。

［1］ASHTON C P，BACON B，DEPLANTE C，et al.3D seismic survey design［J］.Oilfield Review，1994，6（2）：19-32.

［2］张虎，姜建军，蒋先艺.模拟退火算法在海上地震勘探航线优化设计中的应用［J］.石油地球物理勘探，2011，46（1）：12-16.Zhang Hu，Jiang Jianjun，Jiang Xianyi.Application of simulated annealing algorithm in optimization designing for offshore seismic exploration routes［J］.Oil Geophysical Prospecting，2011，46（1）：12-16.

［3］马良.旅行推销员问题的算法综述［J］.数学的实践与认识，2000，30（2）：156-165.Ma Liang.Algorithmic review on the travelling salesman problem［J］.Mathematics in Practice and Theory，2000，30（2）：156-165.

［4］张虎.确定海上拖缆勘探最佳转弯路径的方法：中国，200910243753.4［P］.2009-12-23.

［5］邢文训，谢金星.现代优化计算方法［M］.2版.北京：清华大学出版社，2005：71-94.

［6］KIRKPATRIC S，GELATT C D，VECCHI MP.Optimization by simulated annealing［J］.Science，1983，220：671-680.