基于分形理论的涡轮叶片特征提取

冯驰，胡杨，王兆丰

1.哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001 2.西安航空发动机(集团)有限公司，陕西西安710021

基于分形理论的涡轮叶片特征提取

冯驰1，胡杨1，王兆丰2

1.哈尔滨工程大学信息与通信工程学院，黑龙江哈尔滨150001 2.西安航空发动机(集团)有限公司，陕西西安710021

采用了叶片温度这一叶片质量的重要指标，对数据预处理并进行特征提取，为涡轮叶片建立起特征模型。基于分形理论提取叶片温度信号的3种分形维数特征，结合K-means聚类分析和ReliefF算法计算各特征值的权重，从而建立起涡轮叶片的温度特征模型，实现对涡轮叶片故障的早期预警。统计结果表明，该特征模型能够较好地反映出处于故障状态的涡轮叶片的状态。

涡轮叶片;特征提取;分形理论; K-means; ReliefF

网络出版地址: http://www.cnki.net/kcms/detail/23.1191.U.20150727.0857.001.html

燃气轮机作为国家高技术水平和科技实力的重要标志之一被广泛应用于航空国防和工业发电领域。在它的工作过程中，发动机喷出高速喷气流，同时带动压气机和涡轮继续旋转，涡轮叶片长期工作在高温高压的恶劣环境下，其自身温度过热使寿命受到极大影响，因此对涡轮叶片工作状态的监测具有十分重要的意义。分形理论最基本特点是用分形的数学工具来描述研究客观事物。它跳出了一维的线、二维的面、三维的立体乃至四维时空的传统束缚，更加趋近复杂系统的真实属性与状态的描述，更加符合客观事物的多样性与复杂性［1］。综上所述，文中将分形理论应用于涡轮叶片模型的建立，作为叶片故障诊断的理论依据。文中对涡轮叶片旋转一个周期的温度信号进行预处理，以得到单个叶片的温度信号，提取3种分形维数组成的涡轮叶片特征向量，同时引入K-means聚类分析方法对叶片进行分类，根据分类结果应用ReliefF算法计算各分形维数所占权重，继而形成每个叶片的特征模型。涡轮叶片辐射测温系统的输出信号为电压信号，电压经拟合后变换为温度，为方便起见，文中均直接采用电压表示叶片温度，并未进行电压温度转换。

1　单叶片温度数据分割

文中所采集的每组数据包括多个涡轮旋转周期，短时间内(100 ms)，每个叶片的温度分布几乎不变，因此可将多个周期的数据对齐取平均以减少噪声带来的影响。然而因数据的每个涡轮周期之间不可避免地存在相位偏差，为提高对齐精度，需先对数据进行10倍插值。文中采用的三次样条插值法具有良好的收敛性与稳定性，又有二阶光滑性。使用三次样条法插值前后温度数据局部对比如图1所示。从图中可以看出，插值后数据没有出现畸变，而是变得更加平滑。

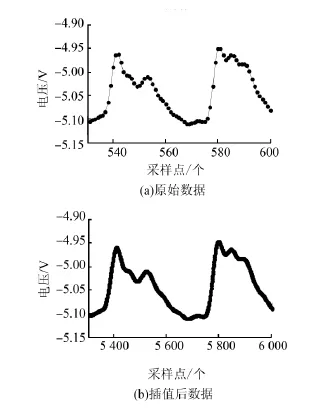
图1　插值前后波形对比

以每周期温度数据的最大值为基准分割出17个周期，计算余下每周期与第一周期数据的相关性，并按照相关性最强点调整对齐。图2为调整前后对比图。

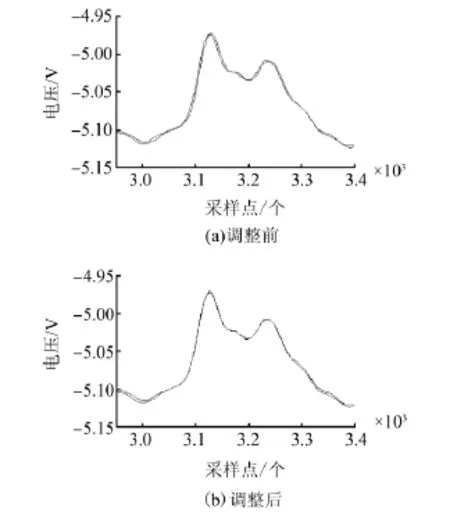
图2　对齐前后波形对比

对齐之后取平均，对这一周期的平均温度信号按极大值分割法(以每个叶片波形的最大的极大值点为基准逐一分割)分出每个涡轮叶片的波形，如图3所示。

图3　叶片波形分割图

文中算法流程如图4所示。

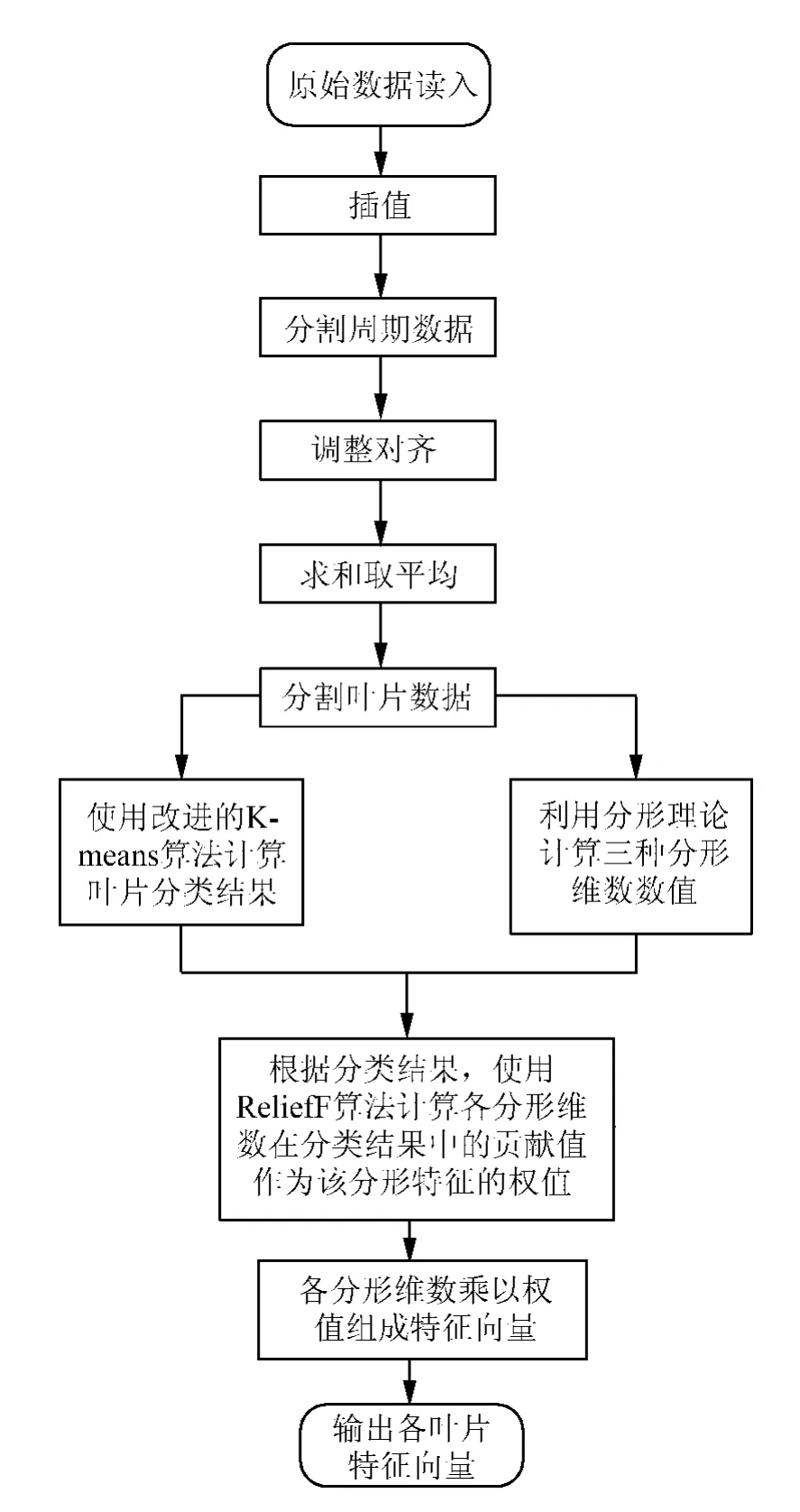
图4　特征提取算法流程

2　特征值计算

2.1分形维数

分形维数［2］是分形意义上由标度关系得出的一个定量数值，可以定量地描述分形集的不规则程度和复杂程度。

2.1.1分形的标度不变性

使用分形理论的前提是需分析的信号具有分形性质。事实上，满足一定条件的动力学系统都会产生分形;反之，判别任意形体是否分形，没有必要从这个形体的产生机制上入手，只要判断它是否具有标度不变性就可以了。

所谓标度不变性是指无论测量尺度如何改变，所测量对象的特性(如形态特性、复杂程度、不规则性、统计特性等)均不发生变化。除了严格的数学模型以外，如Koch曲线，对于实际的分形集来说，这种标度不变性只在一定的范围内适用。通常把标度不变性适用的空间称之为该分形体的无标度区间。

设平面R2内有图形F，在平面内作间距为δ的方格网，则F与方格网相交的方格数Nδ(F )称为图形F在标度(分辨率)δ下的盒数。如果存在一个标度范围(δ1，δ2)，在此范围内log Nδ(F )与log δ保持大约恒定的斜率，则这个范围就称为无标度区。在无标度区内，可以将该形体视为分形。即双对数关系曲线中存在一段直线(或近似直线)，则该段就是无标度区。在该段直线的标度范围(δ1，δ2)内，可以认为波形F是分形，且这段直线的平均斜率就是分形的盒维数，即

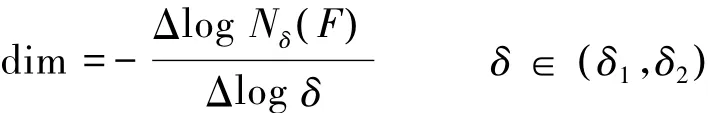
2.1.2分形特性验证实验

基于上述理论，文中将标度定位于(1，80)实验验证涡轮叶片温度曲线是否具有分形特性。从实验所得的log Nδ(F )－log δ双对数曲线来看不易准确判断定位是否为直线段，为此作出斜率与标度的关系曲线，如图5所示。

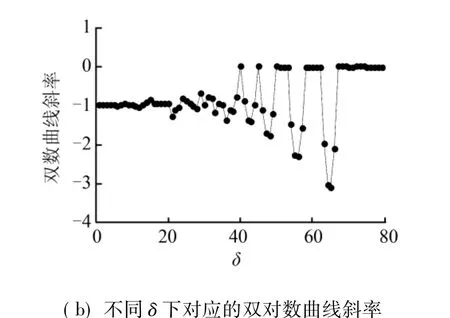
图5 logNδ(F )－logδ双对数曲线及曲线斜率

图中可看出，δ在(1，15)的范围内，斜率值基本保持不变，故可认为无标度区为(1，15)，此处无需精确无标度区范围，只需证明其存在无标度区即可。综上，涡轮叶片的温度信号具有分形特性，事实上，根据分形的定义，文中提取的叶片温度信号的分形特征所反映出的是叶片在分形算法设定区域内的波形分布特征。

2.1.3分形特征值计算

在设备的故障诊断方面，单重分形维数(例如盒维数)只能从单一测度出发描述设备状态信号的分形特征，并不能全面地反映其完整特性。因此文中选用多重分形，计算涡轮叶片温度信号的分形特征，取权重因子q=0、1、2，所对应的分形维数分别为容量维数(盒维数)、信息维数、关联维数［3］。部分叶片的3种分形维数计算结果如表1所示。

表1　第1～5号涡轮叶片的3种分形维数

3　分配特征权重

当一个特征能够清晰刻画形体的时候，类似形体的特征应是相近的，而非类似的形体特征相距较远。因此，具有相似特性的叶片的特征向量之间距离较近，反之较远。而好的特征应该使属于同一类的叶片样本接近，使不同类的叶片样本之间远离。鉴于这种思想，文中使用最常用的K-means聚类算法将叶片分为N类，根据结果使用ReliefF算法计算各分形维数所占权值。

3.1改进的K-means聚类算法

聚类算法是给予数据自然上的相似划分，要求得到的结果是每个类别内部数据尽可能的相似而类别之间要尽可能大的存在差异。K-means算法是常用的基于划分的聚类算法，首先随机选择k个对象作为初始的k个簇的质心，然后将其余对象根据其与各个簇的质心的距离分配到最近的簇;最后重新计算各个簇的质心，不断重复此过程，直到目标函数最小为止［4］。

3.1.1改进方法

K-means算法存在以下缺陷［5］:

1)聚类个数k需要预先给定，而k值选定难估计;

2)对初始聚类中心的选取具有依赖性，算法常常因此陷入局部最优解。

基于上述缺陷，文中采用了改进的K-means算法:

1)最佳聚类数的选择。根据DB Index准则，DBk值越小，说明聚类的效果越好，一般情况下，最佳聚类个数不会超过个，因而迭代算法可以在2～之间进行，在文中选择2～10，选择DB指标最小的聚类数为最佳聚类数。

2)初始聚类中心的选择。普通K-means聚类方法使用随机选择的聚类中心，这使得算法极易陷入局部最优解。文中通过选举机制产生初始聚类中心。具体做法是首先计算最大最小样本点之间的距离d。指定常整数p，k≤p≤N。在N个模式中，找到p个相距较远的样本点。再对p个样本点计算以本身为球心、以d(指定的常数)为半径的球内所包含的样本点个数。选举个数较多的前k个样本点作为初始聚类中心。

3.1.2聚类效果演示

经计算，根据DB Index准则，计算得最佳聚类数为9，图6所示的聚类初始中心点与更新中心点对比图，可见改进的K-means聚类方法没有使聚类结果陷入局部最优解。

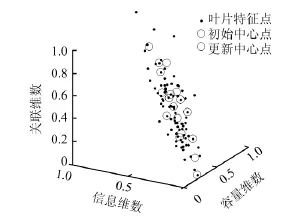
图6　聚类初始中心点与更新中心点图

最后的聚类结果分类如图7所示，表2记录了各分类所包含的涡轮叶片号，基于分类结果，文中采用ReliefF算法计算各分形维数对分类所做的贡献值，以贡献值大小作为该种分形维数的权重。

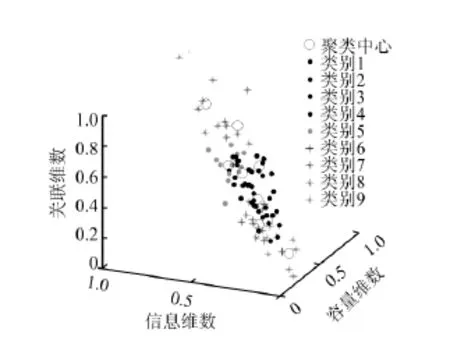
图7　聚类结果分类

表2　各类别所包含的叶片代号(共86个叶片)

3.2基于聚类结果的ReliefF算法

ReliefF算法从训练集D中随机选择一个样本R，然后从和R同类的样本中寻找最近邻的k个样本Hii=1，2，…，k ()，称为Near Hits，从和R不同类的样本中寻找最近邻的k个样本Mi(C ) i=1，2，…，k ()，称为Near Misses，然后根据式(1)更新某个特征A的权重W(A)。

式中: m为重复次数，diff(A，R，S )指的是样本R和S在特征A上的差，p(C )指样本落在集合C中的概率［6-8］。特征的权重越大，表示该特征的分类能力越强，反之，表示该特征分类能力越弱。经计算，叶片的3种分形维数所对应的权值如表3所示。

表3 3种分形维数所对应的权值

将叶片各特征乘以其所对应的权值后，再按改进的K-means算法计算分类后的DB指标，指标从0.286 8降到0.155 7，可见ReliefF算法能有效地提高聚类性能，并且能定量分析各维特征对分类的贡献程度，使叶片温度信号特征更具有代表性。

3.3模拟故障信号及其识别实验

建立叶片特征模型的最终目的是为了能够在叶片发生故障的初期进行预警，提示操作人员停机检查。文中主要研究叶片故障中2种情况:一类是叶片气道大面积堵塞导致整体温度过高。整体温度过高又分为3种情况:前后气道均堵塞，中部正常导致的前缘温度过高，尾缘温度也过高;叶片前缘气道堵塞导致前缘温度过高，使得尾缘气流通过量增大导致尾缘温度过低;前缘温度过低，尾缘温度过高。另一类是叶片局部毛细气道堵塞或者隔热涂层小面积脱落导致局部小范围温度过高。隔热涂层的发射率大概在0.7左右，而金属发射率在0.9左右，因此若叶片的隔热涂层脱落会引起叶片局部的温度偏高，通过斯特藩—玻尔兹曼定律，叶片工作温度在650～750℃的时候，隔热涂层脱落会使得叶片温度上升40℃左右，转换成电压即上升0.14 V左右，为模拟涂层脱落故障的渐变过程，文中仅将电压调整为上升0.8 V。整体温度偏高的故障较为少见，常见故障以局部故障为主［9-10］。

文中使用数学软件MATLAB R2014a版本进行模拟计算，MATLAB具有高效的数值计算及符号计算功能，且提供了大量方便实用的处理工具箱。随机选取正常的第11号叶片温度数据，模拟6个模拟故障信号，其中1号和2号故障数据是通过将正常数据乘以Kaiser窗获得的，其中一个Kaiser窗的衰减参数设为0.3，另一个设为0.4，来模拟叶片前缘、尾缘温度都过高的情况; 3、4号故障数据是通过将正常叶片数据分别通过幅度为0.01和－0.01的正弦窗获得的，用来模拟叶片前缘温度高、尾缘温度低和前缘温度低、尾缘温度高的情况; 5、6号故障数据是将正常数据加上一个以第50数据点和第100数据点为中心，宽度为50个数据点，高度为0.8的高斯窗，用来模拟第50数据点和第100数据点发生局部故障的情况。1、3、5、6号故障数据模拟前后对比如图8所示，图中实线为正常数据波形，而虚线则为故障模拟数据波形。

表4所示的是11号叶片温度信号在未进行求和取平均时在前10个周期的波形所对应的乘权值后的分形特征值及因这10个周期11号叶片波形变化导致的分形特征值变化的范围。由表4可以看出，3种分形维数的变化范围均不超过2%，故将σ=－2%+ 2% []设为置信区间，用来判断叶片是否处于正常状态，此置信区间是根据文中所用数据设置的故障识别门限，因文中的数据量有限，置信区间与实际可能存在出入，具体应用时可根据大量数据样本对故障识别门限进行修改。

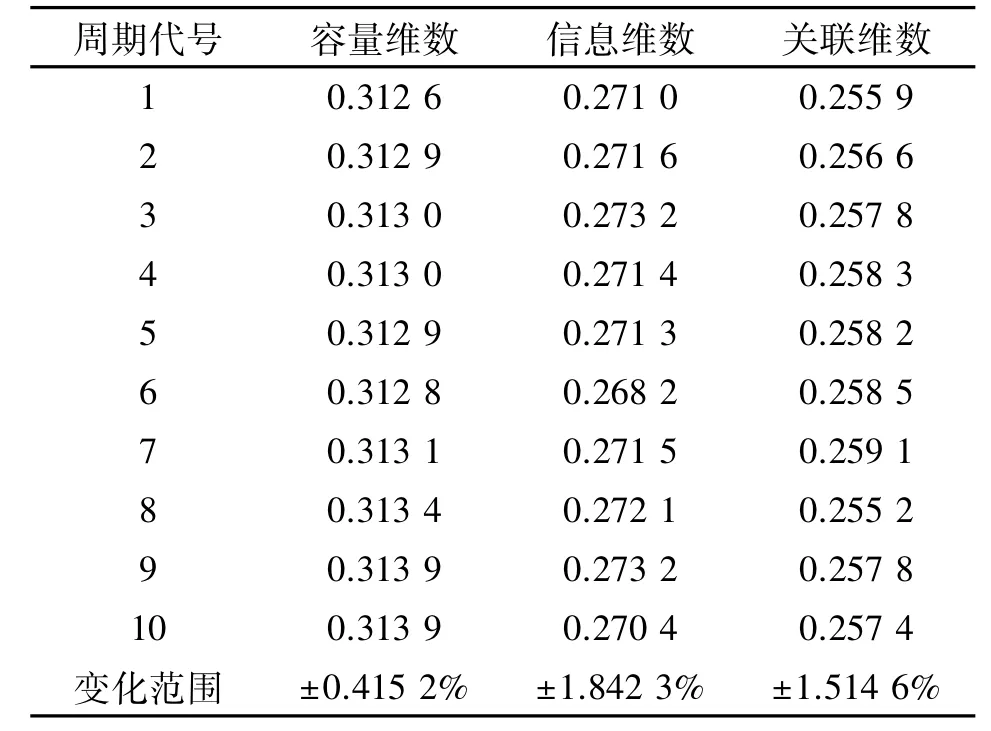
表4 11号叶片10个周期的分形特征及其波动范围

与11号叶片类似，文中使用同样的方式模拟出其他85个叶片对应的6种故障数据，即每种故障均有86个模拟样本。将各故障类型的分形特征与其原始正常波形的分形特征相比较，统计故障分形特征落在置信区间之外不同范围的叶片个数，并计算识别率组成表5。设需判别的某模拟叶片的某分形特征为Dxi，其所对应的正常叶片数据xi同一分形特征为dxi，则识别率η计算公式如下:

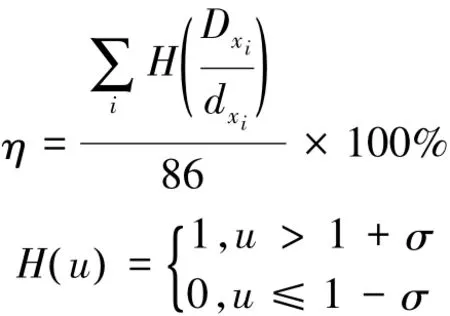
表5　各故障类型分形特征与正常相比偏离超过2%的叶片个数统计表

由表可以看出，模拟的各类故障波形与正常波形相比，均能在分形特征上体现出显著差异，且在关联维数上体现得尤其明显，信息维数其次，容量维数最次，且当增大故障变化的幅度时，识别率能够达到更高。因此，分形特征能够帮助监测人员识别故障叶片以及预测发生何种故障。对于不同种故障，3种分形特征会体现出不同的识别情况，因模拟的故障类型有限，不能对各分形维数最适于识别何种故障类型进行一一讨论。值得一提的是，若使用将原正常波形平移或压缩伸展的方式来模拟故障信号的话，提取出的故障信号的分形特征与正常信号相比，将不会发生变化，这是因为计算分形维数时，算法会先将波形伸展压缩在一个等边长的正方形区域里，这导致无论将原始波形做任何伸展平移，经计算后都会产生同样的结果，事实上，叶片发生故障时不会仅仅是正常波形的单纯平移伸展，所以这种情况可以忽略。综上，文中所研究的涡轮叶片分形特征能显著地反映出叶片故障情况，可以较好地应用于叶片的故障识别中。但故障识别门限以及故障识别类型需大量的具有代表性的正常叶片波形和故障叶片波形样本，因研究条件有限故文中不做深入讨论。

4　结束语

针对涡轮叶片温度信号进行了插值、对齐、分割等数据预处理，通过分形理论提取了温度数据的3种分形特征，并引用经改善过的K-means算法结果和应用ReliefF算法，使得叶片特征按重要性进行权值分配，最后进行了常见叶片故障波形仿真。经统计结果显示，文中提取的特征值能够有效地反映出叶片故障情况，可以应用于叶片的故障识别中。但因本课题研究条件有限，不能深入探究故障识别的具体门限值，接下来的研究重点将放在基于大量具有代表性叶片波形样本的故障识别方向上。

［1］赵玉春.基于混沌分形与模糊聚类的滚动轴承故障诊断［D］.秦皇岛:燕山大学，2011: 36-42.

［2］郝研.分形维数特性分析及故障诊断分形方法研究［D］.天津:天津大学，2012: 35-51.

［3］李兆飞.振动故障分形特征提取及诊断方法研究［D］.重庆:重庆大学，2013: 36-48.

［4］王千，王成，冯振元，等.K-means聚类算法研究综述［J］.电子设计工程，2012(7) : 21-24.

［5］袁方，周志勇，宋鑫.初始聚类中心优化的K-means算法［J］.计算机工程，2007，33(3) : 65-66.

［6］张丽新，王家，赵雁南，等.基于Relief的组合式特征选择［J］.复旦学报，2004，43(5) : 893-897.

［7］张勇.基于ReliefF算法的模糊聚类新算法［J］.应用技术，2009(1) : 43-46.

［8］李晓岚.基于Relief特征选择算法的研究与应用［D］.大连:大连理工大学，2013: 11-30.

［9］刘英乾.涡轮叶片故障诊断与模拟研究［D］.哈尔滨:哈尔滨工程大学，2013: 37-39.

［10］刘大响.航空发动机叶片故障及预防研讨会论文集［C］//北京:航空航天工业出版社，2005: 91-97.

Feature extraction of turbine blades based on the fractal theory

FENG Chi1，HU Yang1，WANG Zhaofeng2

1.College of Information and Communication Engineering，Harbin Engineering University，Harbin 150001，China 2.Xi’an Aero-engine (Group) Ltd.，Xi’an 710021，China

The data is preprocessed and features are extracted to establish a feature model of turbine blades by blade temperature，which is an important indicator of the turbine blade＇s quality.Based on the fractal theory，the three fractal dimension features of blade temperature signals are extracted，the weight of each feature is calculated by combining with K－means clustering analysis and ReliefF algorithm，and thereby establish the temperature feature model of turbine blades，achieving early warning of the turbine blade failure.Statistical results show that the feature model can effectively reflect the state of turbine blades with failure.

turbine blades; feature extraction; fractal theory; K-means; ReliefF

TK473

A

1009-671X(2015) 04-064-06

10.3969/j.issn.1009-671X.201411006

2014-11-14.网络出版日期: 2015-07-27.

黑龙江省自然科学基金资助项目(F201413).

冯驰(1961-)，男，教授;胡杨(1990-)，女，硕士研究生.

胡杨，E-mail: huyang900218@163.com.