弹库出弹平台进给伺服系统定位精度研究与仿真

孙军超，胡逢源，芦晨军，郭春阳，祁松，谢婷婷

1.哈尔滨工程大学机电工程学院，黑龙江哈尔滨150001 2.上海船舶设备研究所，上海200031

弹库出弹平台进给伺服系统定位精度研究与仿真

孙军超1，胡逢源2，芦晨军1，郭春阳1，祁松1，谢婷婷1

1.哈尔滨工程大学机电工程学院，黑龙江哈尔滨150001 2.上海船舶设备研究所，上海200031

弹库的出弹平台用于弹箱在水平方向上的转运与定位，以实现弹箱中弹药的步进式出箱供弹，而要想实现弹药的顺利供弹，弹箱在出弹平台上的定位精度就显得十分重要。针对出弹平台进给伺服系统，依据机械动力学原理，研究了摩擦、间隙和刚度等非线性因素对定位精度的影响，建立了包含有摩擦、间隙和刚度的综合数学模型。利用MATLAB/Simulink对系统进行了动态仿真分析。所得研究结论对实现出弹平台的准确定位提供了理论支撑。

出弹平台;进给伺服系统;定位精度;数学模型; MATLAB/Simulink

网络出版地址: http://www.cnki.net/kcms/detail/23.1191.U.20150727.1037.012.html

近年来随着各种高科技在海战中的应用，人们对舰炮的自动化弹库提出了越来越高的要求，希望其能够快速、稳定、精确地实现自动化供弹过程。弹库的出弹平台作为自动化弹库供弹系统的重要中间环节，其性能的优劣尤其是其顶弹过程中定位的精度直接影响到弹库的供弹过程能否安全可靠的工作，因此对出弹平台的定位精度进行设计研究是至关重要的。出弹平台的定位精度主要取决于进给伺服系统的输出能否准确的跟踪期望的输入要求［1］，因而如果能够减小或消除一些在实际工作中对伺服性能不利的影响因素，这将对提高出弹平台的定位精度产生十分积极的影响。

1　出弹平台系统描述

出弹平台的总体机械结构如图1所示，包括X平台、Y平台和顶弹机构，其主要功能是通过交流伺服电机驱动滚珠丝杠带动工作台在水平方向的X、Y轴上运动，从而将弹箱准确定位到顶弹中心线处，实现炮弹的顺利出箱。

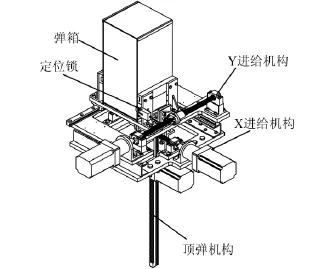
图1　出弹平台机械结构示意图

出弹平台主要依靠进给伺服系统来进行工作，研究出弹平台的工作原理其实就是对进给伺服系统进行研究。进给伺服系统的组成主要包括交流伺服电机、机械传动装置、执行件和检测反馈装置，且该系统设计为如图2所示的全闭环控制系统，位置输入信号为操作人员给出的所希望得到的位置信号，工作台上安装有位移传感器可用来测量工作台上下移动的位置并进行位置反馈，电机上安装有编码器，可用来检测电机转速并进行速度反馈，此外系统还具有电流反馈以保证系统的电流在工作时具有最佳波形。

图2　闭环控制系统方框图

2　系统定位精度的影响因素

进给伺服系统定位精度是通过误差的大小来反映的，而进给伺服系统误差就是指进给伺服系统处于稳定状态时，理想位置和实际位置之差，它反映了系统伺服进给的稳态质量［2］。通过对进给伺服系统的研究分析可以知道对其定位精度产生较大影响的主要有系统刚度、传动间隙、摩擦阻尼等。

2.1刚度对系统定位精度的影响

伺服系统的刚度如果选取不当，会使系统产生弹性变形，造成失动现象，从而严重影响系统的定位精度，必须充分考虑［3-4］。伺服系统的刚度分为机械刚度和伺服刚度。

机械刚度是指元件产生单位变形量所需力的大小，反映了构件抵抗弹性变形的能力，可表示为

式中: F为作用力，N;δx为弹性变形量，m。

伺服刚度与通常所说的机械刚度是两个不同的概念，它是用来表示整个伺服系统抵抗外力而不产生位置偏差的能力，可表示为

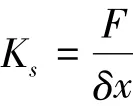
式中: F为外加负载，N;δx为位置偏差，m。

2.2间隙对系统定位精度的影响

系统中的构件在加工和安装过程中往往存在尺寸误差和安装误差，再加上系统过程中存在有变形和磨损等现象，会造成系统传动链中有间隙存在。间隙特性类似于线性系统的滞后环节，但不完全等价，一般会使系统的稳态误差增大，动态性能变差，而由于闭环校正的作用，间隙较小时只会引起滞后，对输出精度影响不大，但当间隙增大到一定数值以后，间隙特性会严重影响系统输出精度和稳定性。设间隙大小为2Δ，则具有间隙的系统输入输出特性如图3所示［5］，数学表达为

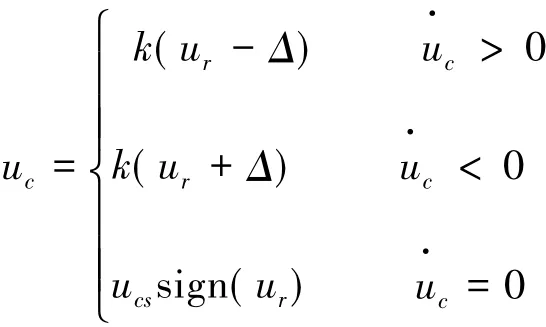
式中: uc为输出量，为输出速度，ur为输入量，k为图3中直线AB和CD的斜率。

图3　带有间隙的输入输出特性

2.3摩擦对系统定位精度的影响

系统在工作时，由于相互接触构件之间的相对运动，不可避免地会产生摩擦阻尼，系统的摩擦阻尼一般分为静摩擦阻尼和动摩擦阻尼，静摩擦阻尼是系统从静止到开始运动的过程中所需克服的阻尼，动摩擦阻尼包括与法向载荷成比例但与速度无关的库伦摩擦阻尼和与速度成比例的粘性摩擦阻尼。摩擦阻尼与速度之间的关系如图4所示［6-7］，当系统开始启动时，由于动静摩擦之间的相互转换，摩擦阻尼具有非线性特性，这将增加系统的静态误差，降低系统精度。

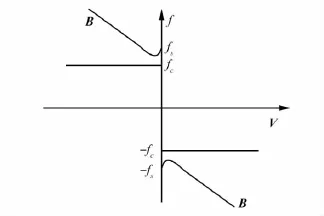
图4　摩擦-速度关系曲线

图4中，V为速度，f为摩擦阻尼，fc为库伦摩擦阻尼，fs为静摩擦阻尼，B为阻尼系数。

3　进给伺服系统数学模型

进给伺服系统主要包括交流伺服电机、伺服控制环路和机械传动装置3部分，分别对这3部分进行分析并建立相应的数学模型。

3.1交流伺服电机的数学模型

由于存在高阶、强耦合、非线性等许多复杂的影响条件，永磁交流同步电机的数学模型属于复杂的多变量系统，为得到合适的电机模型，常采用矢量控制原理来对其进行求解［8］。对电机模型进行研究时，在不影响其控制性能的前提下，通常进行以下假设:

1)定子上的绕组结构均匀、分布对称，且其上的感应电感呈正弦规律;

2)转子上不存在带有阻尼的绕组;

3)不考虑铁芯回路的饱和现象;

4)涡流效应和磁滞现象所产生的损耗忽略不计。

在上述条件的基础上可得永磁交流同步电机的等效电路如图5所示［9］。

图5　永磁交流同步电机等效电路

定子绕组电压方程式可表示为

式中: UM、UT为等效M、T轴的绕组电压，V; iM、iT为等效M、T轴的绕组电流，A; LM、LT为等效M、T轴的电感，H; R为绕组电阻; P为电机极对数;ωe为转子电角速度，rad/s;ω为转子机械角速度，rad/s;ΨN为转子永磁体的等效磁链，Wb。

对于永磁交流同步电机来说，其M、T轴的电感近似相等，即LM=LT，则电机转矩平衡方程可表示为

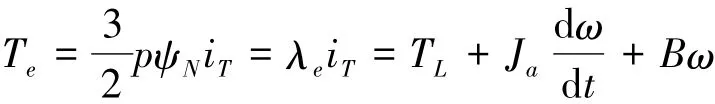
式中:λe为转矩系数，N·m/A; TL为负载转矩，N·m; B为电机的摩擦阻尼系数; Ja为电机轴转动惯量，kg·m2。

采用iM=0的矢量控制方法，电机状态方程可表示为

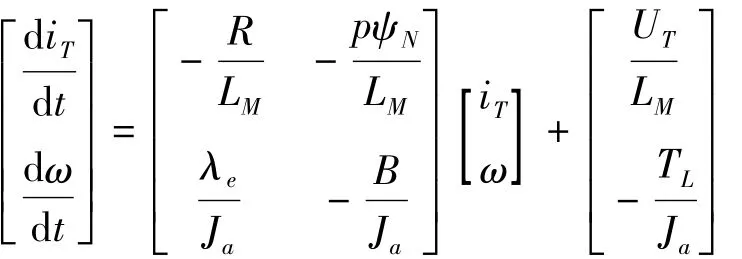
3.2伺服控制环路的数学模型

伺服控制环路包括电流、速度和位置三路，使用三环路控制结构可以使系统获得很好的跟随性能和抗干扰性，对这三路的参数进行适当的调整，可以有效地减少系统超调和误差，调高系统的稳定性和定位精度。

电流环能够实时有效的抑制电流环内的干扰，提高系统的响应速度，限制最大电流，得到适当的输出力矩，从而保障系统的安全运行，电流调节器可采用PI控制器，传递函数可表示为

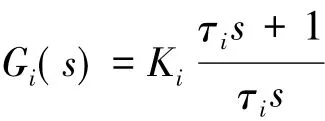
式中: Ki为电流环比例系数，τi为电流环积分时间常数。

速度环能够抑制外来干扰，提高系统动态响应特性和控制精度，速度调节器可采用PI控制器，传递函数可表示为

式中: Kv为速度环比例系数，τv为速度环积分时间常数。

位置环属于伺服系统的外环，好的位置环能够使系统获得很好的定位精度和动态跟踪特性，因而位置调节器采用PID控制器，其传递函数可表示为

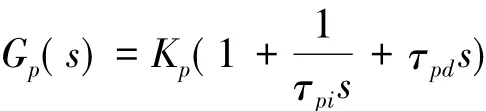
式中: Kp为位置环比例系数，τpi为位置环积分时间常数，τpd为位置环微分时间常数。

3.3机械传动装置的数学模型

机械传动装置主要包括电机、联轴器、轴承、滚珠丝杠副、导轨滑道、工作台等［10］，其简化后的等效动力学模型如图6所示。

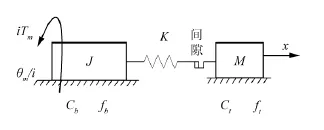
图6　机械传动装置等效动力学模型

对图6中的模型进行研究分析，其动力学方程可表示为

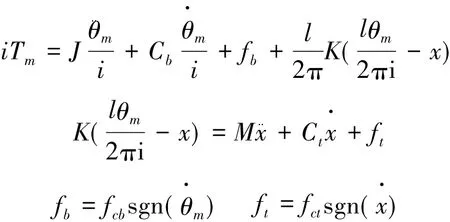
式中: Tm、θm分别为电机轴的输出力矩，N·m和输出转角，rad; J为电机和滚珠丝杠的等效转动惯量，kg·m2; K为系统的等效总刚度，N/m; Cb是轴承及滚珠丝杠副的粘性阻尼，N·s/rad; Ct是导轨的粘性阻尼，N·s/m; l是滚珠丝杠导程，m; x、M分别是工作台的实际位移，m和质量，kg; fcb是轴承及滚珠丝杠副的摩擦力矩，N·m; fct是工作台与导轨之间的摩擦力，N。

3.4进给伺服系统的数学模型

经过上述的研究分析，得到进给伺服系统各组成环节的数学模型，将这些数学模型综合起来便可得到进给伺服系统的数学模型，其数学模型传递函数结构框图如图7所示。

图7　进给伺服系统数学模型框图

4　仿真分析

4.1仿真模型

如今在进行现场试验之前，一般都会先对系统进行计算机仿真，以验证其可行性，MATLAB/SIMULINK作为当今最具有影响力的仿真软件之一，与一般的程序建模不同，其程序设计采用模块化语言，只需将所选取的功能模块用引线连接起来就构成了SIMULINK仿真程序，使用起来更加简便、直观。进给伺服系统利用SIMULINK所建立的仿真模型如图8所示。

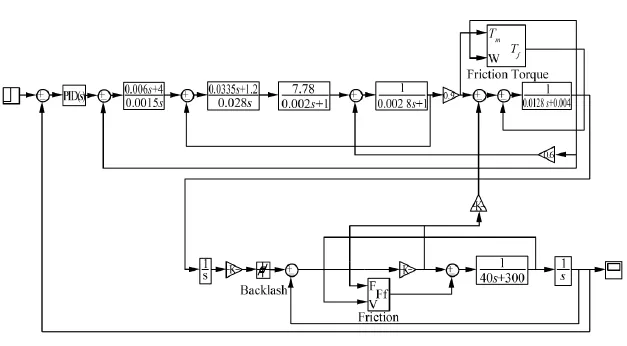
图8　进给伺服系统仿真模型

在进行系统仿真之前，需要先确定各参数的数值。位置环比例系数Kp=50，位置环积分时间常数τpi=0.7，为位置环微分时间常数τpd=0.4，速度环比例系数Kv=4，速度环积分时间常数τv=0.001 5，电流环比例系数Ki=1.2，电流环积分时间常数τi=0.028，PWM逆变器放大系数Kpwm=7.78，时间常数Tpwm=0.002，电枢电感LM=2.8×10-3H，绕组电阻R=1 Ω，转矩系数λe=0.9 N·m/A，电机和滚珠丝杠的等效转动惯量J=1.28×10-3kg·m2，轴承及滚珠丝杠副的粘性阻尼Cb=0.004 N·s/rad，导轨处粘性阻尼Ct=300 N·s/m，滚珠丝杠导程l=0.01 m，工作台质量M=40 kg。

4.2仿真分析

为了消除系统不利因素的影响，获得较好的定位精度，利用MATLAB/SIMULINK对系统进给伺服系统进行仿真，分别研究分析刚度、间隙和摩擦阻尼等因素对系统定位精度的影响。图9～11是在大小为0.06的阶跃信号作为输入的情况下，系统在刚度大小分别为5×105N/m、5×106N/m两种情况下的响应曲线，其中图9是输出响应曲线，图10是误差响应曲线，图11是速度响应曲线。通过对仿真结果进行分析可以看出，当系统的刚度较小时，零部件将会发生较大变形，从而导致输出响应振动较大，稳定性不好，响应速度也有所降低，且输出误差较大。因此实际工作中为得到较好的定位精度，应尽量提高系统部件的刚度。

图9　不同刚度条件下系统输出响应曲线

图10　不同刚度条件下系统误差响应曲线

图11　不同刚度条件下系统速度响应曲线

图12～15分别是存在间隙情况下幅值为0.06的正弦信号和大小为0.06的阶跃信号作为输入时系统的响应曲线。其中图12、13是输入为正弦信号时的输出跟随响应曲线和跟随误差响应曲线，图14、15是输入为阶跃信号时，间隙大小分别为0、0.000 5、0.001 m等3种情况下的输出响应曲线和误差响应曲线。通过对仿真结果进行分析可以看出，当系统具有足够的刚度时，系统中间隙的存在会引起输出响应产生滞后现象，如正弦跟随信号中的“平顶”现象，而且在反向运动时会影响系统稳定性和精度，且这种现象会在间隙的增大时变得越发严重。

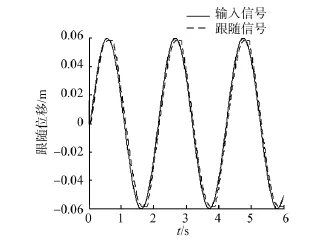
图12　存在间隙时的正弦信号输出跟随曲线

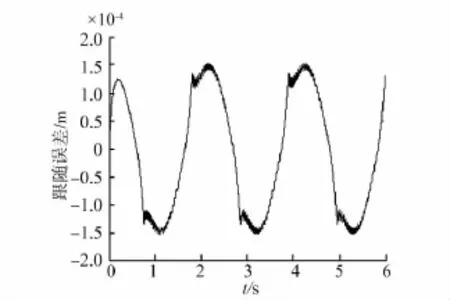
图13　存在间隙时的正弦信号误差曲线

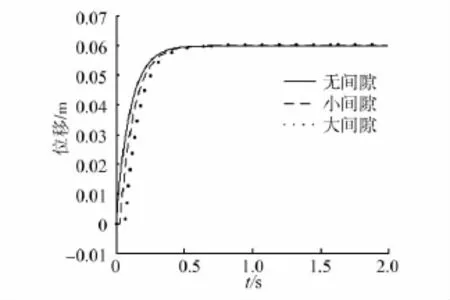
图14　不同间隙条件下阶跃信号响应曲线

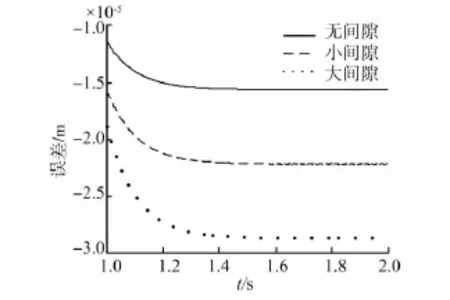
图15　不同间隙条件下阶跃信号误差响应曲线

摩擦阻尼对丝杠进给系统的影响很大，特别是在低速时表现更为明显，而且当进给速度低于某一临界速度时，系统会出现爬行现象。如图16、17所示，当进给速度低于Stribeck速度(1 mm/s)时，进给速度出现了零点跳跃甚至负值，系统的运行出现了爬行现象，造成了系统运行过程的极度不稳定，严重影响了系统的精度。图18是无摩擦、较小摩擦、较大摩擦3种条件下系统输出稳定时的阶跃信号误差响应曲线，从图中可以看出摩擦阻尼的存在会对系统的定位精度产生很大的影响，且这种不好的影响会随着阻尼的增加而增大。因此实际工作中应尽量减小或消除系统的摩擦阻尼，以便获得较好的定位精度。

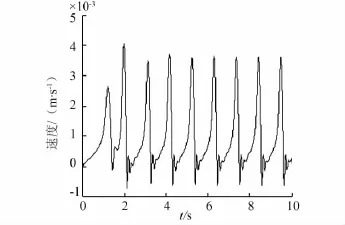
图16　速度为0.9 mm/s时速度响应曲线

图17　速度为0.9 mm/s时位移响应曲线

图18 3种不同摩擦情况下系统误差响应曲线

5　结束语

在弹库出弹平台进给伺服系统定位精度的研究过程中，充分考虑了刚度、间隙和摩擦阻尼等影响因素，建立了带有间隙模块和摩擦阻尼模块的进给伺服系统数学模型，并利用MATLAB/SIMULINK对其进行仿真分析。仿真结果表明，提高系统刚度能够减少系统失动量，有利于提高系统的定位精度，而摩擦阻尼和间隙的存在则会导致系统稳态误差的增加，降低系统定位精度。因此，根据理论分析，合理的设定系统的间隙和刚度等参数，能够使弹库出弹平台获得满意的定位精度。

［1］刘丽兰，刘宏昭，吴子英.考虑摩擦和间隙的机床进给伺服系统建模与分析［J］.农业机械学报，2010，41(11) : 212-218.

［2］韦富基，谭顺学.高精度机床伺服进给系统精度研究［J］.制造业自动化，2012，34(5) : 69-71.

［3］吴南星，胡如夫，孙庆鸿.数控车床丝杠进给系统刚度对定位精度的影响［J］.中国工程科学，2004，6(9) : 46-49.

［4］张兆凯，唐苗，曹东海，等.电动伺服系统刚度问题研究［J］.微特电机，2012，40(7) : 5-8.

［5］虞文华.具有间隙非线性的伺服进给系统对轮廓加工误差的影响机理［J］.浙江大学学报，1999，33(6) : 608-611.

［6］张立勋，董玉红.机电系统仿真与设计［M］.哈尔滨:哈尔滨工程大学出版社，2006: 171-175.

［7］董亮，唐文成，刘立.考虑摩擦和间隙的柔性滚珠丝杠进给系统建模与分析［J］.农业机械学报，2013，44(11) : 300-307.

［8］陈先锋.伺服控制技术自学手册［M］.北京:人民邮电出版社，2010: 32-34.

［9］SATO R，TSUTSUMI M.Modeling and controller tuning techniques for feed drive［J］.Proc of the ASME，Dynamic Systems and Control Division，Part A，DSC74 -1，2005(3) : 669-679.

［10］VARANASI K K，NAVFEH S A.The dynamics of leadscrew drives: low -order modeling and experiments［J］.ASME J DynSyst Meas Control，2004(126) : 388-396.

Research and simulation on positioning accuracy of the feeding servo system of a magazine＇s jacking shells device

SUN Junchao1，HU Fengyuan2，LU Chenjun1，GUO Chunyang1，QI Song1，XIE Tingting1

1.College of Mechanical and Electrical Engineering，Harbin Engineering University，Harbin 150001，China 2.Shanghai Marine Equipment Research Institute，Shanghai 200031，China

The jacking shells device of a magazine is used for cartridge box＇s transport and positioning，so as to realize the shell＇s single launch，and the positioning accuracy is very important to ensure the launching smoothly.Focusing on the feeding servo system of the jacking shells device of a naval gun，this article researches the influence of friction，clearance and stiffness on the positioning accuracy，establishes a comprehensive model which contains friction，clearance and stiffness on the basis of the mechanical dynamics principle，and analyzes the system＇s dynamic characteristics by MATLAB/Simulink.The conclusion provides theoretical support for the positioning accuracy of jacking shells device.

jacking shells device; feeding servo system; positioning accuracy; mathematical model; MATLAB/Simulink

TJ818

A

1009-671X(2015) 04-001-07

2014-12-15.网络出版日期: 2015-07-27.

国家自然科学基金资助项目(51175099).

孙军超(1989-)，男，硕士研究生.

孙军超，E-mail: 959877288@qq.com.

10.3969/j.issn.1009-671X.201412012