从命题的视角谈“平面向量”的复习

☉江苏省清浦中学 吴洪生

从命题的视角谈“平面向量”的复习

☉江苏省清浦中学 吴洪生

向量是既有大小又有方向的量.大小反映了向量“数”的特征，方向反映了向量“形”的特征.它兼具“数”与“形”的双重身份，兼具代数的抽象与严谨和几何的直观与形象；既是“代数”与“几何”沟通的纽带，又能充分体现数形结合思想；也能体现形象思维与逻辑思维的结合.它是中学数学一个重要的知识交汇点，在高考中备受命题者青睐.

一、高考定位

平面向量模块共考查1个A级考点、4个B级考点、1个C级考点.要深刻理解A、B、C等级的含义，A级未必很容易，C级未必就很难.

（1）平面向量的概念是本模块第一个最重要、最基础的概念，是基础的基础，也是第一个B级考点，对后续内容的学习与研究至关重要.

（2）平面向量的线性运算与坐标表示作为两个B级考点，主要考查：向量加法、减法及数乘运算的含义及其几何意义；向量加法的平行四边形法则及向量加法、减法的三角形法则；用坐标表示平面向量的加法、减法与数乘运算.

（3）向量共线与垂直也是B级考点，主要考查：两个向量共线与垂直的含义；平面向量的平行与垂直的充要条件；向量共线定理及向量共线与垂直的坐标表示.

（4）《考试说明》虽然没有把平面向量的基本定理作为考点专门列出，但平面向量的基本定理及基本运算，在高考中占居重要地位，时常出现在各地模考与高考试卷中.

（5）平面向量的数量积作为高考8个C级考点之一，应当引起高度的重视.主要考查：平面向量数量积的含义；平面向量的数量积与向量投影的关系；数量积的坐标运算；运用数量积表示两个向量的夹角等.

（6）《考试说明》虽然只将平面向量的应用列为A级考点，但由于近几年高考试题加强了对知识性和应用性的考查，常常在知识交汇处命题，考查时常将向量融入三角、平几、解几等问题之中，突出向量的工具作用.

二、考点整合

1.平面向量的两个重要定理

（1）向量共线定理：向量a（a≠0）与b共线当且仅当存在唯一的一个实数λ，使b=λa.

（2）平面向量基本定理：如果e1，e2是同一平面内的两个不共线向量，那么对这一平面内的任一向量a，有且只有一对实数λ1，λ2，使a=λ1e1+λ2e2，其中e1，e2是一组基底.

（1）零向量模的大小为0，方向是任意的，它与任意非零向量都共线，记为0.

（2）长度等于1个单位长度的向量叫单位向量，与a同向的单位向量为

（3）方向相同或相反的向量叫共线向量（平行向量）.

（4）向量的投影：|b|cos＜a，b＞叫做向量b在向量a方向上的投影.

4.平面向量的几个重要结论

（1）向量共线的充要条件：O为平面上一点，则A，B， P三点共线的充要条件

5.两非零向量平行、垂直的充要条件

设a=（x1，y1），b=（x2，y2），则：

（1）若a∥b⇔a=λb（b≠0）；a∥b⇔x1y2-x2y1=0；

（2）若a⊥b⇔a·b=0；a⊥b⇔x1x2+y1y2=0.

三、命题视角

视角一：平面向量的运算

1.平面向量的线性运算

2.平面向量的坐标运算

例2如图2，在四边形ABCD中，AB=2，AD=1，三角形BCD为正三x，y的值.

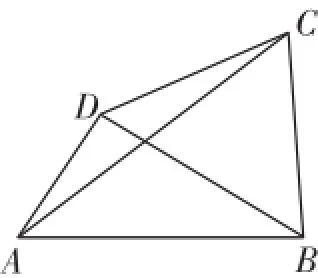
图2

以A为坐标原点，AB所在直线为x轴建立如图3所示的直角坐

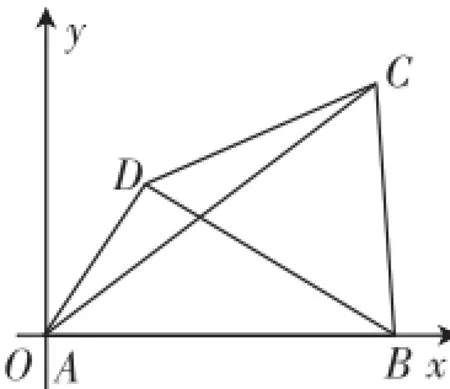
图3

说明：对于相对特殊的图形也经常考虑建系，运用坐标进行有关的运算，这就是通常所说的坐标法.通过建立坐标系，将向量用坐标表示，主要考查向量的坐标运算与坐标法.

方法总结：（1）平面向量的运算主要包括线性运算与坐标运算，不少问题既可用线性运算，也可用坐标运算，解决问题的关键是看哪种运算方便.

（2）向量的线性运算，一般是选择一组基底，若已知某两向量的模、夹角，往往尝试以这两向量为基底，将有关向量用基底线性表示.通常的处理方法是利用“平行四边形法则”或“三角形法则”合成或分解.

（3）解决向量的坐标运算问题，关键是掌握线性运算法则及坐标运算的特点.一般地，已知有向线段两端点的坐标，应先求出向量的坐标.解题时注意利用向量相等（横、纵坐标分别相等）建立方程（组）的思想.

视角二：平面向量的数量积

1.平面向量的模

例3（常州市2015届高三）已知向量a=（1，1），b=（-1，1），设向量c满足（2a-c）·（3b-c）=0，则|c|的最大值为_________.

解法一：设c=（x，y），则（x-2，y-2）·（x+3，y-3）=0，即（x-2）（x+3）+（y-2）（y-3）=0（表示圆），则|c|的最大值为

说明：|c|的几何意义为圆上的动点到原点的距离.

解法二：由（2a-c）·（3b-c）=0可得c2-（2a+3b）·c=6a· b=0.所以|c|2-|c·||2a+3b|·cosθ=0.

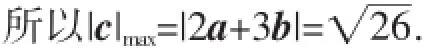
方法总结：高考对平面向量的模的考查，常考查的类型有：

（1）把向量放在适当的坐标系中，给有关向量赋予具体坐标求向量的模，如向量a=（x，y），求向量a的模只需利用公式|a|=即可求解.有时需要充分运用代数、几何、三角等工具.

（2）不把向量放在坐标系中研究，求解此类问题的通常做法是利用向量运算法则及其几何意义或应用向量的数量积公式，关键是会把向量a的模进行如下转化：|a|=

2.平面向量的夹角

例4（2014年四川卷）平面向量a=（1，2），b=（4，2），c=ma+b（m∈R），且c与a的夹角等于c与b的夹角，则m= _________.

A．－2B．－1C．－1D．2

解法二：由几何意义知c为以ma，b为邻边的菱形的对角线向量，又|b|=2|a|，故m=2.

方法总结：高考对平面向量夹角的考查.常见类型：

（1）依条件等式，运算求夹角，在此类问题的求解过程中应关注夹角的取值范围.

（2）依已知图形求两向量夹角，此类题求解过程应抓住“两向量共起点”，便可避开陷阱，顺利求解.

（3）两向量夹角公式其实是平面向量数量积公式的变形和应用.

3.平面向量的数量积

说明：处理向量的数量积的三种常用手法：定义法、基底法和坐标法.本题用定义法最为简洁，用坐标法也可以得出同上结论，另由两个直角三角形拼接的平面图形，计算角的最值，可转化到直角三角形用两角和与差的正切来解决，体现了化归与转化的思想.

方法总结：高考对平面向量数量积的考查.常见类型：

（1）求解几何图形中的数量积问题，通过对向量的分解转化成已知向量的数量积计算是基本方法，但是如果建立合理的平面直角坐标系，把数量积的计算转化成坐标运算也是一种较为简捷的方法.

（2）求向量的数量积的公式有两个：一是定义式a· b=|a|·|b|cosθ；二是坐标式a·b=x1x2+y1y2.

视角三：平面向量的应用

1.平面向量与三角形

例6在△ABC中，M是BC的中点，AM=3，BC=10，则

解析：由余弦定理AB2=AM2+BM2-2AM·BM· cos∠AMB=52+32-2×5×3cos∠AMB，AC2=AM2+CM2-2AM·CMcos∠AMC=52+32-2×5×3cos∠AMC，∠AMB+∠AMC=180°，两式子相加为AC2+AB2=2AM2+2CM2=2×

方法总结：平面向量与三角形结合的问题，往往是以向量为载体，去研究三角形的问题，充分利用三角形内角和定理、正余弦定理、面积公式、向量夹角公式、向量平行与垂直的充要条件、向量的数量积等知识.既能考查解三角形的知识与方法，又能考查运用三角公式进行恒等变换的技能.

2.平面向量与三角函数

（2）记f（x）=m·n，在△ABC中，角A，B，C的对边分别是a，b，c，且满足（2a-c）cosB=bcosC，求函数f（A）的取值范围.

方法总结：在平面向量与三角函数的综合问题中，平面向量的知识主要是给出三角函数之间的关系，解题的关键还是三角函数问题.一方面用平面向量的语言表述三角函数中的问题，如利用向量平行、垂直的条件表述三角函数式之间的关系，利用向量模表述三角函数之间的关系等；另一方面可以利用三角函数的知识解决平面向量问题.在解决此类问题的过程中，只要根据题目的具体要求，在向量和三角函数之间建立起联系，就可以根据向量或者三角函数的知识解决问题.平面向量和三角函数的图像和性质相结合的题目，是高考最近几年出现的热点题型.此类题目要求在熟练掌握平面向量和三角函数图像的基础上要对平面向量和三角函数的性质能够灵活运用.

3.平面向量与解析几何

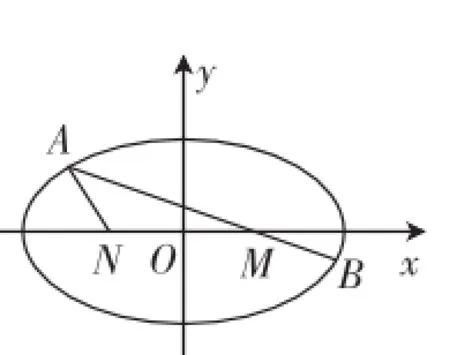
图4

方法总结：解析几何中向量知识只是给出几何量的位置和数量关系，在解题中要善于根据向量知识分析解析几何中的几何关系.解析几何与向量结合，既能考查圆锥曲线的知识与方法，又能考查向量的基本方法.平面向量与解析几何之间转化的主要手段是向量的坐标运算.

高考对“平面向量”的考查已在注重基础和概念的同时，逐渐加强综合性，以考查学生综合运用知识的能力.因此，在平面向量的复习教学中，首先，要注重基本概念和基本运算的教学，概念要深刻理解、运算要准确无误，尤其是向量互相垂直、平行的充要条件和平面向量基本定理、向量共线定理（包括坐标运算），应熟练掌握、运用自如；其次，教学中应把向量与其他知识内容进行融会贯通，将平面几何、解析几何、解三角形、三角函数等问题与平面向量融合，充分揭示数学中化归思想的深刻内涵.由于向量形式具有多样性、运算具有灵活性，因此，向量问题具有多角度、多层次、多方位的思维空间，从而使向量成为“在知识交汇点处设计试题”的很好载体，成为高考的热点内容之一.F