高压水除鳞气动管路的发热分析与改进

刘彦川，张韫韬，雷亚勇

(秦皇岛首秦金属材料有限公司，河北秦皇岛066326)

高压水除鳞系统的工作原理是利用高压水喷出时产生强大冲击力和冲刷力，基体材料和氧化铁皮层因冷却收缩率不同而产生剪切力，水渗入基体材料和氧化铁皮之间产生蒸汽膨胀爆裂，在钢坯表面形成类似切削、爆破的效果，使氧化铁皮破碎成小碎片并与钢坯表面迅速脱离，按设定方向冲掉氧化铁皮。

某公司4 300 mm 一期高压水除鳞系统由营口流体集团设计，如图1 所示。

图1 高压水除鳞系统示意图

自投产以来，与压力容器——气水罐相连接的管道表面温度有时高达70 ℃左右，远高于压力容器的出厂温度最高值50 ℃，如图2 所示。

图2 与气水罐连接的气动管路

长期高温使用，压力容器的强度将下降，容易发生蠕变现象，加剧压力容器内部防腐材料的剥落及内部的腐蚀，一定条件下会发生氢脆现象，直接影响到气水罐的使用寿命，严重时甚至发生高压泄漏，影响人生安全。

更换一个压力容器，需要13 天左右完成吊装、安装、管路焊接、补气过程，备件费用高达80 万元。对于宽厚板生产线而言，压力容器能否按照周期正常使用，直接关系到安全生产，影响到钢板产量和质量。因此对气动管路内部压缩空气过度发热问题进行定量分析，提出具体的改进措施具有重大意义，为二期配套完善工程项目提供具有理论意义的指导方案。

1 高压水除鳞系统的原理及设备参数

1.1 除鳞系统工作原理

如图1 所示，除鳞蓄势罐组是由1 个10 m3的气水罐、2 个10 m3的气罐组成。气水罐的最高工作压力为19.5 MPa，最低工作压力为16 MPa。除鳞泵升降速由气水罐压力上、下限对耦合器进行控制。钢坯经过一次除鳞箱时，1 号喷射阀组打开，高压水喷射在钢坯上进行一次除鳞，钢坯离开除鳞箱咬入轧辊前，2 号喷射阀组打开，高压水对钢坯进行二次除鳞。气水罐压力在除鳞过程中迅速下降，当压力降到下限时，耦合器的调速装置——操作勺管径向缩回，增加壳体内的油环厚度，即增加工作腔中的油量，耦合器输出转速提高，除鳞泵在耦合器控制下升速运行，向气水罐补充高压除鳞水。当气水罐压力达到设定上限时，耦合器的调速装置——操作勺管径向伸进，减小壳体内的油环厚度，即减小工作腔中的油量，耦合器输出转速降低，使除鳞泵在耦合器控制下降速运行，等待下一个除鳞周期。

1.2 除鳞系统设备参数

气水罐的压缩空气是靠2 个气罐提供，当磁浮子液位计的显示达到5 水位时(即5.6 m 时) ，空压机对气罐进行补气。2 个气罐连接蓄势器之间的管道为内径65 mm 的无缝钢管。高压气罐设备参数见表1，一次除鳞设备参数见表2，高压离心泵参数见表3。

表1 高压气罐设备参数

表2 一次除鳞设备参数

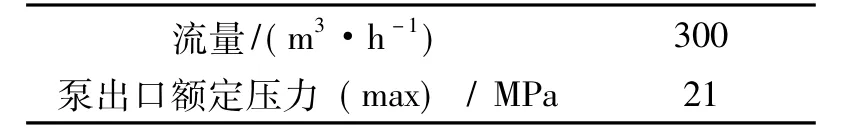
表3 高压离心泵参数

三通气闸阀通径为DN65 mm，管路具体参数如表4 所示。

表4 管路参数 mm

2 气动管道的流速与温度分析

2.1 管道流速分析

根据气体动力学原理，压缩空气在管路流动过程中，压力损失是引起管壁温度变化的主要原因。文中分析的对象是1 号气闸阀与气水罐入口之间的一段垂直管路，该管路压降变化表现在喷射阀组打开，对钢坯进行除鳞的过程中。除鳞过程中，当气水罐内部的水压低于某一值时，除鳞泵和气水罐同时供水。由于一次除鳞和二次除鳞的用水量不同，所以文中主要分析用水量最大的一次除鳞过程。

钢坯通过一次除鳞箱时，从开始除鳞到除鳞结束，大约为7 s 左右，在除鳞泄压过程中，气罐中的压缩空气向气水罐迅速流动。按照设计要求，气水罐的压力范围为: pmax=19.5 MPa，pmin=16 MPa。

气水罐释放压力的过程如图3 所示。

图3 气水罐泄压过程

p1= 19.5 MPa，p2= 16 MPa，V1= 1.739 2 m3(气水罐5 水位时的容积参数)

假定在除鳞降压过程中，气水罐从高水位开始供水，则整个过程分两部分解体考虑: 当气水罐压力由19.5 MPa 下降到16 MPa 时，内部体积先做等熵变化; 气罐向气水罐补气时，气体体积再一次做等熵变化［2］，气压由19.5 MPa 降到16 MPa。

第一个等熵变化过程:

p2=16 MPa，则V2=1.962 3 m3(V2为气水罐内部体积做等熵变化后膨胀的体积) 。

气水罐在7 s 内供水量为V排=Q·t=280 m3/h·7 s=1.08 m3，则气水罐在除鳞完毕，水位下降后的气体体积V3为:

则: V3=1.08 +1.739 2－1.962 3 =0.86 m3

补入气体体积第二个等熵变化过程:

则: V补=0.746 6 m3

由此计算出7 s 内，管道AB 段内径D =65 mm时，气体流速v1为:

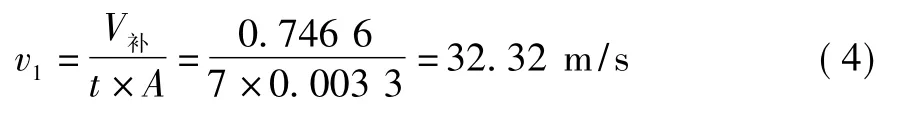
根据工程设计标准，车间内管道的压缩空气流速一般取v=10 ～15 m/s［1］，由此可见，气水罐在工作过程中，气动管道内部气流速度远远超过工程设计极限，因此可判断原除鳞气动管路存在设计问题。

由式(3) 可以看出: 在现有工况不变的情况下，增大气体流动面积，可有效减少管道内部的气流速度。

4 300mm 一期项目投产之初，国内高压气闸阀的最大通径为DN65 mm，营口流体设计的气动管路的尺寸为φ89 mm ×12 mm，与气水罐外接管路尺寸φ102 mm×18 mm，基本实现等径连接，接头处的压力损失基本为0。

根据韦斯巴赫的实验数据，气水罐外接管路尺寸φ102 mm×18 mm 保持不变，气动管路AB 段内径过大，节流作用带来的压力损失将会影响到气罐给气水罐正常补压。因此，选取合理的气动管路内径，最大程度降低因增粗管路带来的压力损失，是解决目前问题的关键因素。

若按照工程设计标准，气流速度采用最高值15 m/s，气体体积流量不变，则气体管道内径D≈95 mm; 气流速度采用最低值10 m/s 时，则气体管道内径D≈116 mm。

因此合理的气动管道内径D 应该为:

为保证选取的管道内径既能降低气流速度，又能减少压力损失，文中选取该范围的中间数: D =105 mm，通过温度分析，进一步优化内径。

由此可见，合理选取管道内径是降低气体流速、减小压力损失的方案之一。

2.2 管道内部温度分析

增粗管道内径后对气动管道温度变化的具体影响，以及选取的管道内径D =105 mm 能否满足压力容器的设计温度值是文中研究的关键问题。

根据传热学原理，管道内强制对流的换热分析与一系列涉及流动及换热的条件有关。对高压水除鳞气动管路内部气流的温度分析，首先需要对流动状态进行判断。在流体力学界，有层流与湍流之分，其分界点的临界雷诺数Re=2 300。Re ＜2 300 为层流区，Re＞10 000 为旺盛湍流区，而一般认为2 300 ＜Re ＜10 000 的范围是过渡区［3］。

2.2.1 层流换热

对于管内层流换热，一般采用齐德－泰勒公式来计算长度为l 的管道的平均Nu 数［3］:

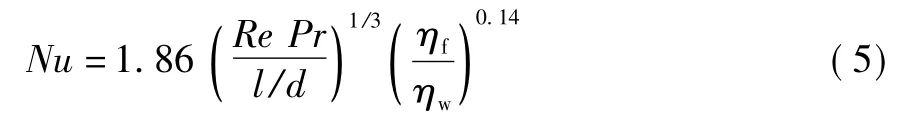
式中: Nu 为努塞尔数，反映壁面上流体的量纲为一的温度梯度;

Re 为雷诺数;

l 为管道特征长度;

d 为管道内径;

ηf为按流体平均温度计算的流体动力黏度;

ηw为按流体壁面温度计算的流体动力黏度;

Pr 为普朗特数，反映流体中动量扩散与热扩散能力的对比。

2.2.2 湍流换热

对于管内湍流强制对流换热，使用最广的关联式为迪图斯－贝尔特(Dittus－Boelter) 公式［3］:

式中: Nu 为努塞尔数，量纲为一;

Re 为雷诺数;

加热流体时，n=0.4;

Pr 为普朗特数，反映流体中动量扩散与热扩散能力的对比。

设定2 个气罐的压缩空气汇合到1 号三通气闸阀时，温度为T1，经过管道AB 段后，气体温度为T2。按照气罐的设计要求，T2≤50 ℃。

根据气动管路内部气体的流动状态，选择合理的换热关联式，计算出管道内表面的传热系数，由此可分析出管道内径变化时，其内壁表面温度的动态变化差距。设定文中研究的压缩空气在经过管路AB 段前后，平均温度为50 ℃左右，由文献［3］附录查询气体在50 ℃时的相关参数如表5 所示。

表5 文中研究气体的相关参数

2.2.2.1 管道内径D=65 mm 的传热系数

式中: v 为管路内部流速;

d 为管道内径;

νf为运动黏度。

此时气体流动状态处于旺盛湍流区，湍流切应力(雷诺应力) 使得气流温度升高较快，计算该直径大小内压缩空气的传热系数应采用关联式(5) ，由此得出:

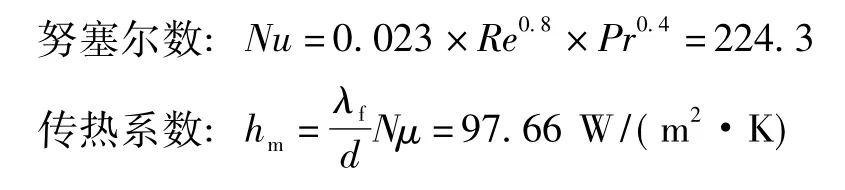
2.2.2.2 管道内径D=105 mm 的传热系数

此时气体流动状态也处于旺盛湍流区，计算该直径大小内压缩空气的传热系数同样采用关联式(5) ，由此得出:

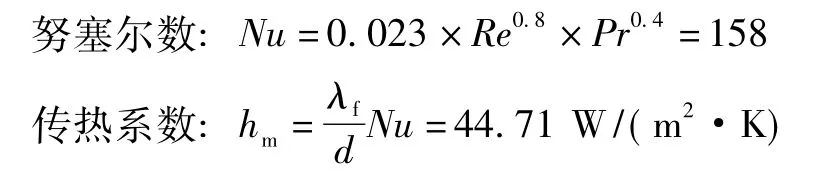
2.2.3 三通气闸阀前后温差变化

管道BC、CD 段内径为90 mm，气罐到气闸阀的管道内径为65 mm，DN65 mm 的气闸阀开口度达到最大。因此，在气水罐补气过程中，压缩空气经过3号气闸阀，在CD 段流动时是一个扩张段形式，气体在这段管路中是体积膨胀的过程，对气流温度影响较小。气体从CD 段管道流向2 号气闸阀时，是一个节流过程，这个过程气流不做功，由于局部受阻，会有压力降产生。节流过程认为是绝热，但有摩擦，所以节流过程可以看作是一个绝热熵增过程，节流前后的焓近似不变，所以节流前后温度变化不大。

因此，在气动管路的内径变化时，气体从气罐开始给气水罐补气的过程中，经过1 号气闸阀的出口温度T1相同，管道内壁温度与气体平均温度差也保持不变，则由热平衡方程式可计算出内径改变前后管路内壁表面温度的动态变化差距。

气流管道的热平衡方程［3］为:

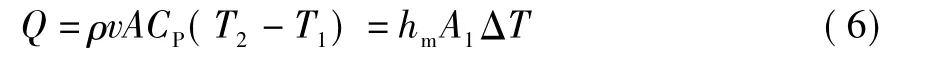
式中: ΔT 为管道内壁温度与气体平均温度差;

A1为一定长度管道的内表面面积(A1=π·D·L) ;

D 为管道内径;

L 为管道长度;

A 为管道横截面积;

T2为气动管路出口温度;

T1为气动管路入口温度;

CP为比热系数。

根据前面小节计算的传热系数，由热平衡方程关联式(6) 可得:

管路内径D=65 mm 时，气流出口温度:

同理可得，管路内径D =105 mm 时，气流出口温度T3为:

整理关联式(7) 、(8) ，可得到管道直径改变前后，管道内气流出口温度的变化函数关系:

当管路内径D 为65 mm、出口温度为70 ℃时，则:

若经过1 号气闸阀温度为30 ℃，则

根据关联式(9) ，可计算出管路内径D 为105 mm 时的出口温度T3:

简化为摄氏度，则t3为:

综上所述，当选取管道内径D=105 mm，出口温度为38.9 ℃，完全满足压力容器的温度要求。同理可得，管道内径D =95 mm，气动管路出口温度接近60 ℃。由此可见，保证压力容器温度要求的合理管道内径近似在100 mm 左右。

由此可见，气动管路的直径变化直接影响到压缩空气对管道内部的传热系数。直径越大，传热系数越小，同等入口温度下，出口气流温度变化差异越小。

3 气动管路的改进措施

结合文中对高压除鳞系统气动管路发热问题的理论分析及结论，2010年4月，在首秦公司4 300 mm二期配套升级改造工程中，对一期高压水除鳞系统气水罐的气动管路进行增粗改造。

一期工程设计之初，高压三通气闸阀的国标最大值为DN65 mm。目前，国内高压三通气闸阀的标准最大值为DN80 mm。因此，二期工程中，除鳞蓄势罐选用了国标最大通径的高压气闸阀，与管道尺寸实现等径连接，减少气闸阀局部压力损失，如图4 所示。

图4 改造后的三通气闸阀

4 结论

运用空气热力学、流体力学、传热学等方法，对高压水除鳞系统气动管路的发热问题进行理论分析。通过分析得出: 管道内的气流速度超过了一般工程设计标准，管壁气温升高的主要原因在于其内部气流速度过快所致。通过选取合理的管道内径、选用开口度较大的高压三通气闸阀(DN80 mm) ，有利于降低管道内表面温度，保证压力容器的内部温度不超过50 ℃。

目前，气水罐压缩空气管路的外表温度在改造后，稳定在40 ℃左右，保证了压力容器在正常、合理的周期内安全使用。研究结果与实践表明: 文中的理论分析对改造工作具有指导意义，为特种设备的安全使用提供了基础性保障。

［1］路甬祥．液压气动技术手册［M］．北京: 机械工业出版社，2004:770－785，938．

［2］崔凯．粗轧机高压水除鳞系统的改造［J］．机床与液压，2007，35(10) :208－209．

［3］杨世铭．传热学［M］．北京: 高等教育出版社，2006:45－427．