萤火虫算法-投影寻踪模型在云南省洪灾评估中的应用

刀海娅,孙 艳

(云南省水利水电勘测设计研究院,云南 昆明 650021)



萤火虫算法-投影寻踪模型在云南省洪灾评估中的应用

刀海娅,孙 艳

(云南省水利水电勘测设计研究院,云南 昆明 650021)

洪灾评估;投影寻踪;萤火虫算法;云南省

1 研究背景

洪灾在我国发生频率高,危害范围广,不但造成严重的经济损失并危及人民的生命财产安全,而且易导致滑坡、泥石流等次生灾害,极大地制约了经济社会的持续健康发展。开展洪灾评估可以客观评估洪灾对灾区社会经济的影响,为防汛抗旱、民政救灾等部门提供决策依据,并提高洪灾管理效率。目前用于洪灾评估的方法主要有GIS法[1]、模糊综合评判法[2]、层次分析法[3]、神经网络法[4]以及投影寻踪法[5]等,这些方法均在洪灾评估中取得了一定的实际应用效果。投影寻踪(projection pursuit,PP)法是将高维数据投影到低维子空间上,并在该子空间上寻找出能够反映原高维数据结构或特征的投影的统计方法[6-7],在克服“维数祸根”以及解决小样本、超高维等问题中具有明显优势。在实际应用中,PP模型最佳投影方向a的选取对于PP模型的泛化性能及评估结果有着关键性影响。目前,常用于PP模型a选取的智能方法有遗传算法(genetic algorithm,GA)[7-9]、粒子群优化 (particle swarm optimization,PSO)算法[10]等,这些方法在提高PP模型预测或评估精度上取得了较好的效果。Yang[11]通过对萤火虫个体相互吸引和移动过程的研究,提出了一种新型群体智能优化算法——萤火虫算法(firefly algorithm,FA)。该算法是模拟自然界中萤火虫的发光行为而构造出的一种随机优化算法,具有计算效率高、设置参数少、操作简单、易于实现等优点,已在图像处理、函数优化、路径规划等领域得到了广泛应用,但鲜见于PP模型的参数优化。

本文选取农作物受灾面积、受灾人口、死亡人口、倒塌房屋间数、直接经济损失作为洪灾评估指标,利用PP模型对洪灾进行评估,并针对PP模型在实际应用中存在的问题,采用FA算法优化PP模型的a,建立FA-PP洪灾评估模型,并与PSO-PP模型进行对比。

2 FA-PP洪灾评估模型

2.1 PP模型

PP模型简要算法过程如下[12-14]。

(1)

式中:x(i,j)为第i年第j个评估指标值;xmax(j)、xmin(j)分别为评估数据集中第j个评估指标的最大、最小值;n、m分别为总年数及评估指标数。

(2)

式中:a为单位长度向量。

c. 优化投影指标函数。当投影指标函数取得最大值时,所对应的a方向为最能反映数据特征的最优投影方向。因此搜寻最优投影方向问题就转化为非线性最优求解问题,即:

(3)

式中：Sz为z(i)的标准差；Dz为z(i)的局部密度。

(4)

(5)

e. 评估。将a代入式(2)得到各年度z(i),依据洪灾分级标准进行评估。

2.2 萤火虫算法

根据文献[15-18],从数学角度对萤火虫算法的优化机理进行描述。

a. 相对荧光亮度I。萤火虫I的计算公式为

(6)

式中:I0为萤火虫最大荧光亮度,其值与目标值有关,目标值越优则I0值越大,表示亮度越高;γ为光强吸收系数,表示荧光在传播过程中被媒介吸收,随距离增加而衰减;rgh表示萤火虫g与萤火虫h间的距离。

b. 相对吸引度β。萤火虫g、h间的β计算公式为

(7)

式中:β0为最大吸引度。

c. 位置更新:萤火虫g被吸引向萤火虫h移动的位置更新为

(8)

式中:Xg、Xh为萤火虫g和h所处的空间位置;α为步长因子,α∈[0,1];rand()∈[0,1]上的随机数,且服从均匀分布。

从式(8)可以看出,扰动项α(rand()-1/2)在一定程度上可加大搜索区域,避免FA算法过早陷入局部最优。

2.3 FA-PP洪灾评估模型实现步骤

a. 数据预处理。利用式(1)对数据进行归一化处理,设置萤火虫数M、最大吸引度β0、光强吸收系数γ、步长因子α、最大迭代次数T。

b. 确定目标函数。由于FA算法是求解极小值,因此将式(3)的倒数作为目标函数,即以式(9)作为适应度函数:

(9)

c. 初始化操作。随机初始化萤火虫位置Xg(g=1,2,…,k),每个萤火虫位置对应一个5维向量a,由式(9)计算优化目标适应度值,将该值作为萤火虫g的自身I0,并找出当前群体中处于最佳位置个体,判断算法迭代终止条件是否满足,若满足,转向步骤h;否则,执行步骤d。

d. 利用式(6)、式(7)计算群体中萤火虫的I以及β,根据I决定萤火虫移动方向。每只萤火虫都移向相对于它亮度最高的萤火虫。

e. 利用式(8)更新萤火虫的空间位置,对处在最佳位置的萤火虫进行随机扰动。

f. 根据更新后萤火虫的位置,按式(9)重新计算优化目标适应度值,将该值作为新的萤火虫亮度值,并找出当前萤火虫所处最佳空间位置。判断算法迭代终止条件是否满足,若满足则转至步骤g;否则重复执行步骤d—f。

g. 输出最优个体值和全局极值,即最佳投影方向a[a(1)a(2)a(3)a(4)a(5)]和Q′(a)。

i. 评估。将a代入式(2)得到各年度洪灾z(i),并依据所构造分级标准进行洪灾评估。

3 应用实例

3.1 数据来源

本文根据云南省2001—2013年《水利统计年鉴》资料,选取农作物受灾面积、受灾人口、死亡人口、倒塌房屋间数、直接经济损失作为洪灾评估指标,见表1。

表1 云南省2001—2013年洪灾基本评估指标

3.2 算法参数设置及验证

a. 参数设置。FA算法:T=200,M=30,β0=1,γ=0.5,α=0.2。PSO算法:T=200,M=30,惯性因子ω=0.728,局部和全局搜索学习因子c1=1.5,c2=1.7。

b. 算法验证:依据表1洪灾资料,利用FA算法及PSO算法对式(9)进行极值寻优,并将FA算法及PSO算法连续运行4次,得到Q′(a)、向量a[a(1)a(2)a(3)a(4)a(5)]以及进化过程图,见表2和图1。

表2 FA、PSO算法最优个体值和全局极值

图1 FA算法和PSO算法连续运行4次进化过程

a. 从表2和图1可以看出,在保留8位有效数字的情况下,FA算法4次连续运行的Q′(a)值均为0.002 622 10,而PSO算法Q′(a)值在0.002 622 10～0.002 622 12之间,FA算法收敛精度优于PSO算法。

b. 在保留4位有效数字的情况下,FA算法4次连续运行的a均为(0.418 6 0.531 9 0.447 5 0.485 4 0.325 6),a取值范围变化稳定;而PSO算法a分别在(0.417 6～0.420 6 0.530 9～0.532 3 0.447 0～0.448 5 0.483 5～0.486 0 0.324 3～0.326 4)之间波动,a取值范围变幅相对较大。

上述验证表明:FA算法具有较好的收敛精度、稳健性能和全局寻优能力,利用FA算法寻优a,可有效避免a取值范围变幅过大的缺陷。

3.3 构造分级标准

3.4 评估

将a(0.418 6 0.531 9 0.447 5 0.485 4 0.325 6)代入式(2)可以得到云南省2001—2013年洪灾z(i),并依据所构造的分级标准进行洪灾评估,结果见表3及图2。

表3 云南省2001—2013年洪灾评估结果

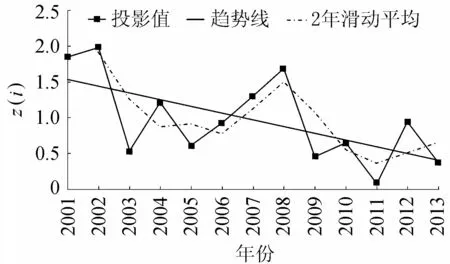
图2 投影值变化趋势及2年滑动平均过程

b. 从a=(0.418 6 0.531 9 0.447 5 0.485 4 0.325 6)来看,各评价指标a(j)均为正值,说明各评价指标投影方向一致。其中受灾人口投影分量最大,可认为受灾人口对云南省洪灾影响最大;其次为农作物受灾面积、死亡人口和倒塌房屋间数；而直接经济损失对云南省洪灾影响最小。

c. 从洪灾影响变化趋势来看,云南省防洪减灾工程建设及中小河流综合整治工程的推进是影响洪灾呈显著减弱趋势的主要因素。

4 结 论

针对PP模型在实际应用中存在的问题,提出FA模型与PP模型相融合的FA-PP洪灾评估模型,以云南省2001—2013年洪灾评估为例进行实例验证,结果表明:

a. FA算法具有较好的收敛精度、稳健性能和全局寻优能力,利用FA算法寻优PP模型a,不但有效避免了a寻优结果变幅过大的缺陷,提高了PP模型的评估精度,而且为解决PP模型a的问题提供了一种新的途径和方法。

b. 从2001—2013年实例洪灾评估结果来看,云南省洪灾随时间呈显著减弱趋势,受灾人口对云南省洪灾影响最大,直接经济损失影响最小。

[ 1 ] 莫建飞,陆甲,李艳兰,等.基于GIS的广西洪涝灾害孕灾环境敏感性评估[J].灾害学,2010,25(4):33-37.

[ 2 ] 刘合香,徐庆娟.区域洪涝灾害风险的模糊综合评价与预测[J].灾害学,2007,22(4):38-42.

[ 3 ] 崔东文.基于人工神经网络与主成分分析法的洪灾评估:以文山州1990—2007年洪灾评估为例[J].水资源研究,2011,32(2):37-39.

[ 4 ] 杨聪辉,王宝华,付强,等.洪水灾情评价的脉冲耦合神经网络模型[J].灾害学,2010,25(3):12-15.

[ 5 ] 陈曜,丁晶,赵永.基于投影寻踪原理的四川省洪灾评估[J].水利学报,2010,41(2):220-225.

[ 6 ] 付强,赵小勇.投影寻踪模型原理及其应用[M].北京:科学出版社,2006.

[ 7 ] 王柏,张忠学,李芳花,等.基于改进双链量子遗传算法的投影寻踪调亏灌溉综合评价[J].农业工程学报,2012,28(2):84-89.

[ 8 ] 陈曜,丁晶,赵永.基于投影寻踪原理的四川省洪灾评估[J].水利学报,2010,41(2):220-225.

[ 9 ] 付强,付红,王立坤.基于加速遗传算法的投影寻踪模型在水质评价中的应用研究[J].地理科学,2003,23(2):236-239.

[10] 陈广洲,汪家权,解华明.粒子群算法在投影寻踪模型优化求解中的应用[J].计算机仿真,2008,25(8):159-161,165.

[11] YANG Xinshe.Nature-inspired metaheuristic algorithms[M]. Beckington:Luniver Press,2008.

[12] 余航,王龙,文俊,等.基于投影寻踪原理的云南旱灾评估[J].中国农学通报,2012,28(8):267-270.

[13] 付强,赵小勇.投影寻踪模型原理及其应用[M].北京:科学出版社,2006.

[14] 崔东文，郭荣.SSO-PP模型在水源地安全保障达标评价中的应用[J].水利经济，2015，33(5)：8-13.

[15] 莫愿斌.群智能算法在经济模型中的应用[M].北京:人民邮电出版社,2014.

[16] 刘长平,叶春明.一种新颖的仿生群智能优化算法:萤火虫算法[J].计算机应用研究,2011,28(9):3295-3297.

[17] 王吉权,王福林.萤火虫算法的改进分析及应用[J].计算机应用,2014,34(9):2552-2556.

[18] 符强,童楠,赵一鸣.一种基于多种群学习机制的萤火虫优化算法[J].计算机应用研究,2013,30(12):3600-3603.

刀海娅(1983—),女,云南勐海人,工程师,主要从事水利工程及水文分析研究。E-mail:65026918@qq.com

10.3880/j.issn.1003-9511.2015.06.005

P333

A

1003-9511(2015)06-0022-04

2015-05-14 编辑：胡新宇)