满堂扣件式脚手架在不同剪刀撑下的有限元分析
何夕平,李 洋,何三军,计洋海,陈 燕,邵传林
(1.安徽建筑大学 土木工程学院,安徽 合肥 230601;2.中国十七冶集团有限公司,安徽 马鞍山 243001)
满堂扣件式脚手架在不同剪刀撑下的有限元分析
何夕平1,李 洋1,何三军2,计洋海1,陈 燕1,邵传林2
(1.安徽建筑大学 土木工程学院,安徽 合肥 230601;2.中国十七冶集团有限公司,安徽 马鞍山 243001)
剪刀撑能够提高满堂扣件式脚手架的整体稳定性,加强脚手架纵横杆、立杆等部位的连接,在传递荷载等方面发挥着重要的作用。通过MIDAS/GEN有限元分析软件建立3×3跨的满堂式扣件脚手架模型,模拟在不同的剪刀撑设置情况下及相同荷载作用下,研究脚手架立杆应力及架体位移的变化规律。其结果可作为研究满堂扣件式脚手架应力传递以及脚手架实际工程中水平、斜向剪刀撑设置等方面提供相应的借鉴和参考。
满堂扣件式脚手架;剪刀撑;应力;位移;刚性模型
扣件式钢管脚手架作为浇筑混凝土模板支撑体系在工程中普遍使用,它具有运输快捷、施工方便等优点。但由于扣件式钢管脚手架搭设是人工操作,其整体稳定性受到人为因素影响比较大,在实际工程中引起的安全事故也较多。鉴于施工安全事故频发,政府对于建筑安全研究越来越重视,相关机构和科研人员针对不同的脚手架进行模拟试验,并通过相应的结构分析软件进行模拟研究,取得了很多成果。陆征然、陈志华等利用ANSYS分析软件研究了脚手架在施加不同荷载下的应力变化情况[1-3],并根据试验的结果与现行规范《建筑施工扣件式钢管脚手架安全技术规范》模板支架的计算方法进行对比,指出规范中的一些不足并提出了相应的改进措施。熬鸿斐、李国强等对于双排式钢管脚手架极限承载力进行分析,并取得了一系列的成果[4]。双排脚手架水平方向设有连墙杆和揽风绳,其整体稳定性有所提高,其相关理论研究可以为满堂扣件式钢管脚手架研究提供相应的参考。满堂脚手架由于跨度长、高度大等特点,其整体稳定性比双排脚手架差,在大面积、大跨度的满堂脚手架工程中,脚手架安全性应引起足够的重视。
本文在《建筑施工扣件式钢管脚手架安全技术规范》的基础上[5],运用MIDAS/GEN 结构分析软件建立5个与现场试验架体相类似的模型,研究5种不同架体(剪刀撑位置不同)在相同荷载下的应力分布及位移变化规律。本文研究结果可以为满堂扣件式钢管脚手架的内力传递规律以及实际工程中剪刀撑设置等研究提供参考。
1 脚手架分析模型建立
1.1 模型概况
满堂扣件式钢管脚手架在纵横方向是由不少于3排的立杆构成,并与水平杆、扫地杆、斜撑等构件通过扣件连接形成的承力支架。大面积满堂扣件钢管脚手架杆件应力传递、变化规律较为复杂,且不便于分析。本文只考虑3×3跨的满堂脚手架体系,在此基础上研究其应力、位移的变化规律。架体立杆间距为0.95 m×0.95 m,步距为1.25 m,扫地杆的高度为0.05 m,架体总高为3.8 m,结构模型如图1所示。第1层平面如图2所示。为研究剪刀撑拆除对于架体内力、位移的影响,剪刀撑一共设置四根:竖直方向设置两个斜向剪刀撑,分别布置在架体的内部(见图3、图4);水平剪刀撑考虑交叉布置可能导致某一层刚度较大,实际模型分别在架体的第二层、第三层各设置一根(见图5、图6)。为研究剪刀撑对于满堂脚手架应力及位移变化的影响,每次荷载加压完毕后,拆除1个剪刀撑,在有限元结构分析软件帮助下,观察架体立柱每根钢管的应力变化并进行对比,同时模拟架体在竖向荷载作用下各节点沿x、y、z方向的位移变化。该试验为竖向荷载试验,不考虑水平荷载和风荷载,不设置侧向支撑。16根立杆具体编号规则如下:上面第一排从左到右依次为1#、2#、3#、4#,第二排5#、6#、7#、8#,第三排、第四排以此类推,1#、2#斜撑的布置如图3、图4所示,架体其余尺寸如图2~图7所示(粗色线表示剪刀撑)。
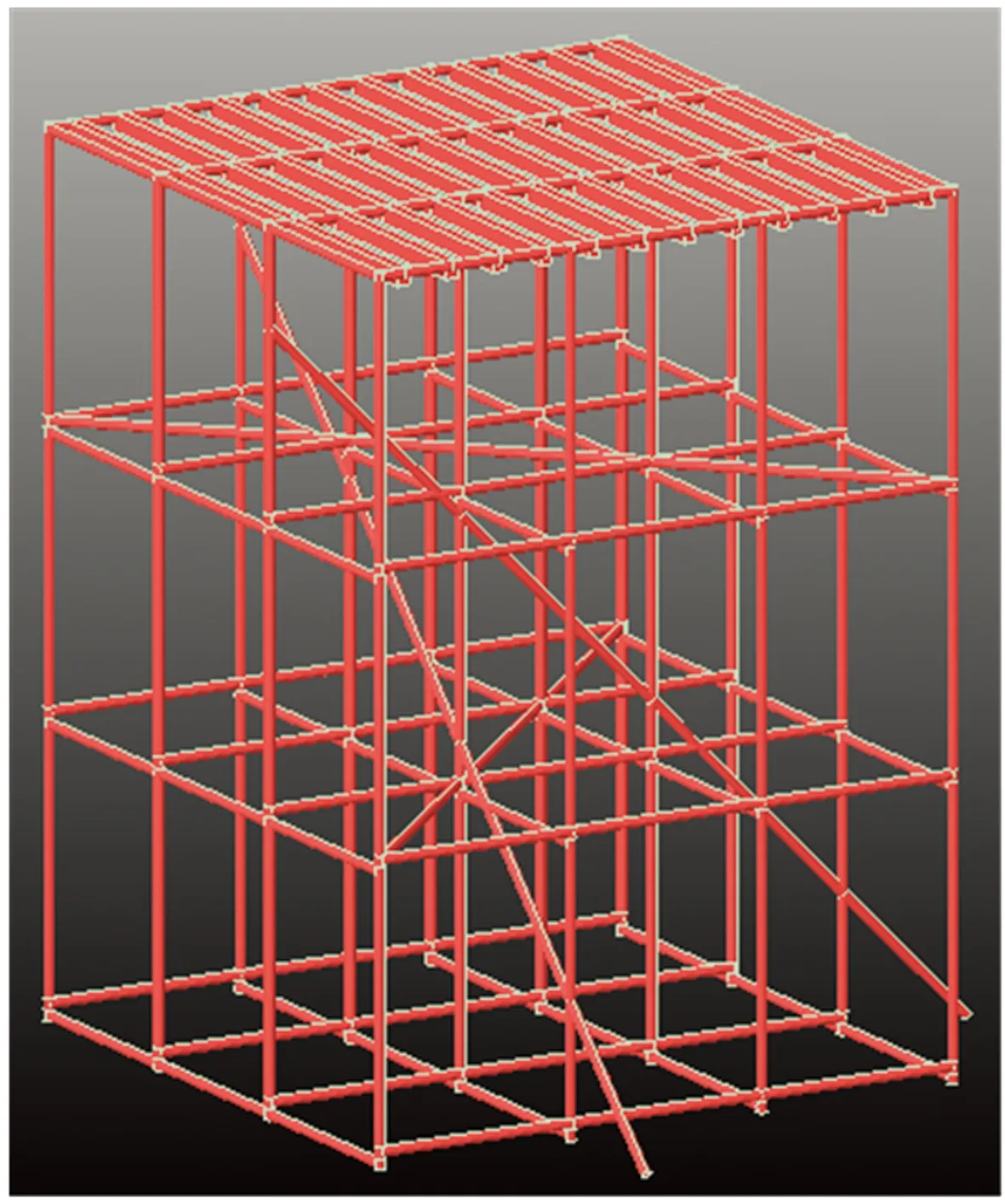
图1 结构模型
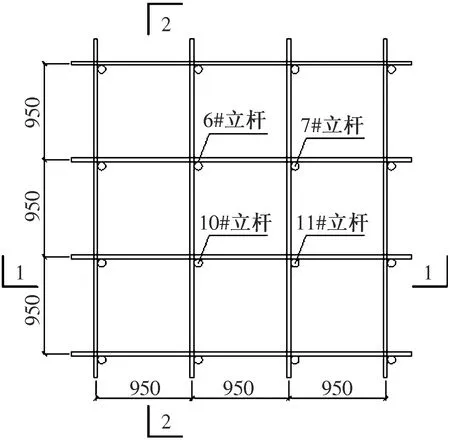
图2 第1层平面图(单位:mm)
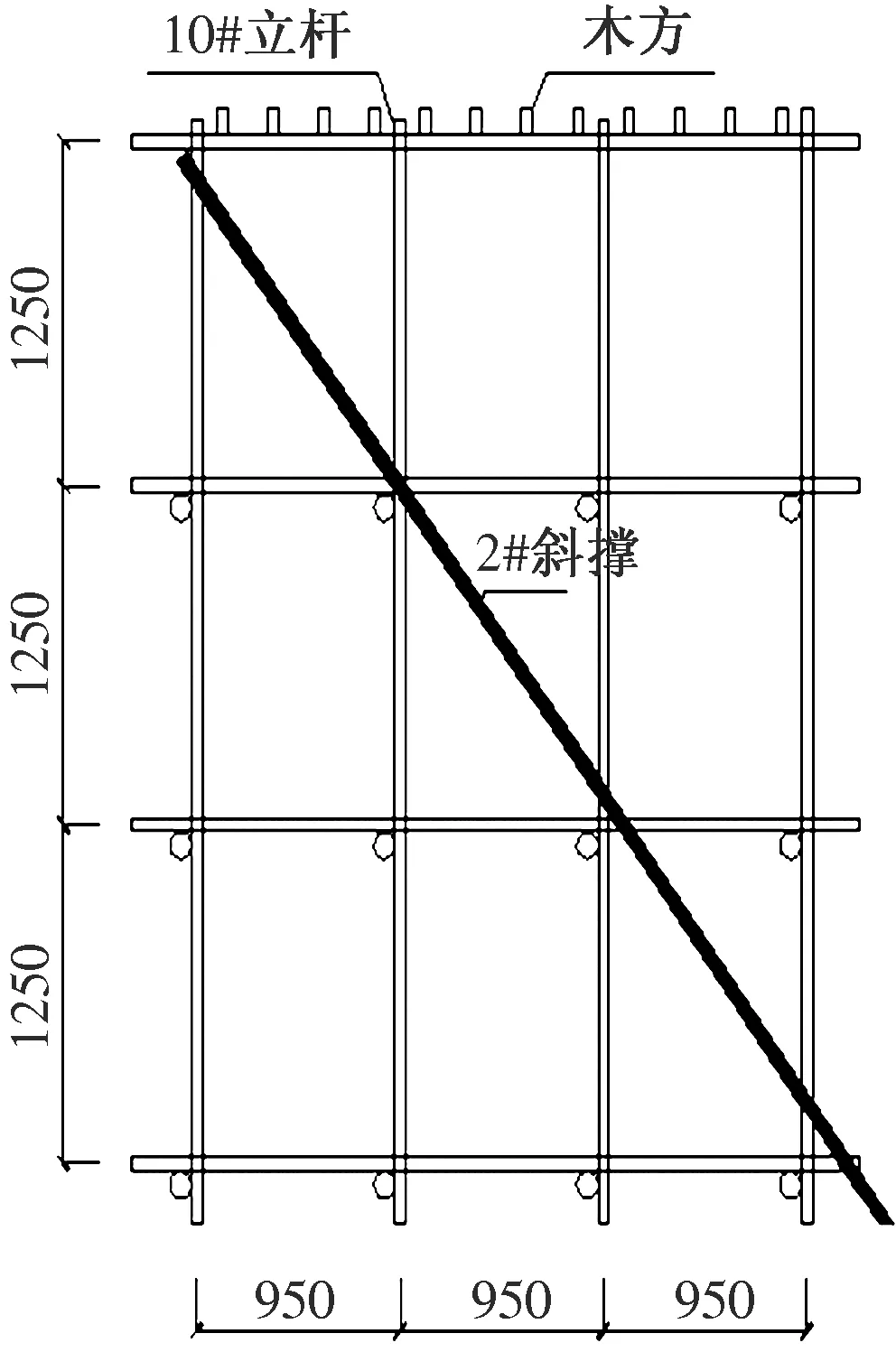
图3 1-1剖面图(2#斜撑)(单位:mm)

图4 2-2剖面图(1#斜撑)(单位:mm)
1.2 模型建立
模型钢管截面采用ø48.3×3.6,材质选用Q235,弹性模量Es取2.06×105MPa。架体顶部设有横向的木方,木方尺寸为68 mm×80 mm,材质为松木,具体参数可参考相应的《木结构设计规范》[6]。顶部荷载采用单向板传力方式,荷载通过单向板→木方→水平杆→钢管立柱路径传给地面。
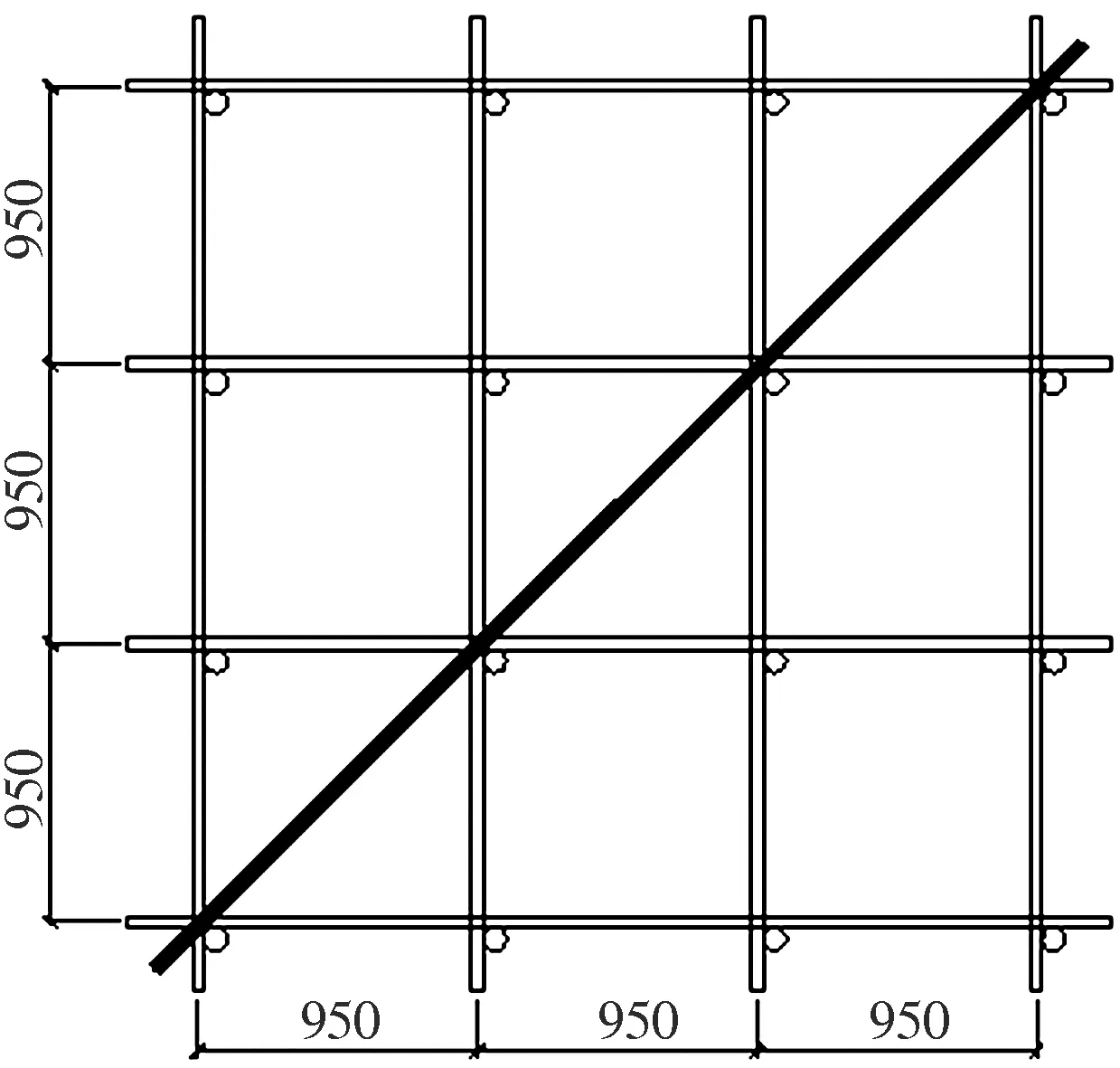
图5 第2层平面图(单位:mm)
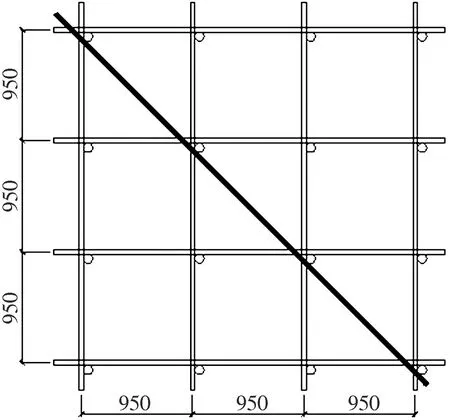
图6 第3层平面图(单位:mm)
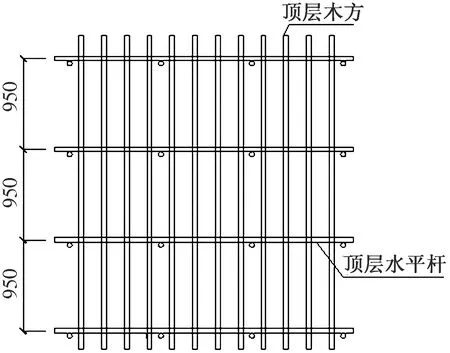
图7 顶层平面图(单位:mm)
本文采用MIDAS/GEN分析软件建模[7~9],水平纵横杆、立杆交界处竖直方向错开0.05 m,扣件连接处采用刚性连接。
2 模型分析计算
结构模型按照拆除脚手架的顺序情况共分为完整架体(简称完架)、拆除3层水平剪刀撑(简称拆一水)、拆除1#斜撑(简称拆一斜)、拆除二层水平剪刀撑(简称拆二水)、拆除2#斜撑(简称拆二斜)共5种工况。顶部荷载分别从2 kN/m2到15 kN/m2(每级增加1 kN/m2)进行加载,模型试验的顺序分别为:完架、拆一水、拆一斜、拆二水、拆二斜,每次只拆除1根水平剪刀撑或斜向剪刀撑。
2.1 应力变化
图8~图12显示了架体在荷载达到15 kN/m2时,不同剪刀撑条件下各架体杆件的应力分布。根据试验结果及应力分布图不难发现,在荷载加载到最大值时,架体内部的4根立杆(6#、7#、10#、11#)轴向应力较大,外围立杆的轴向应力较小,4根角部立杆(1#、4#、13#、16#)应力最小,说明架体内部立杆承受较大的荷载,外围立杆承受的荷载较小。考虑内部立杆应力的增减直接影响整个架体的稳定性,为研究不同剪刀撑对架体应力、位移变化的影响,本文试验将中间四根立杆(6#、7#、10#、11#)的应力值设为参考值,观察不同剪刀撑条件下立杆应力变化规律。架体中间立杆(底部)的应力数值如表1所示。

图8 完架条件下的杆件应力分布
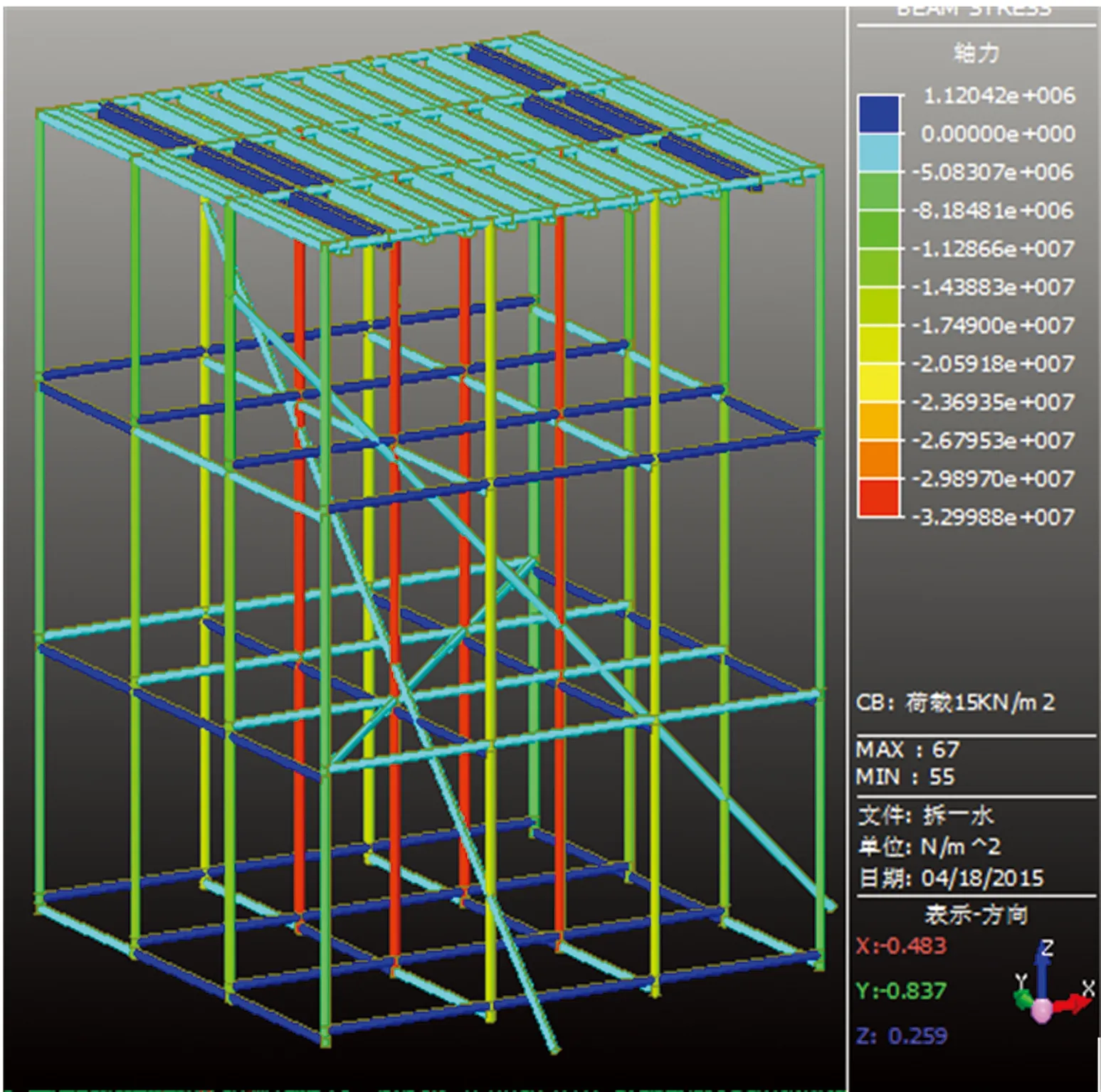
图9 拆一水条件下的杆件应力分布

图10 拆一斜条件下的杆件应力分布
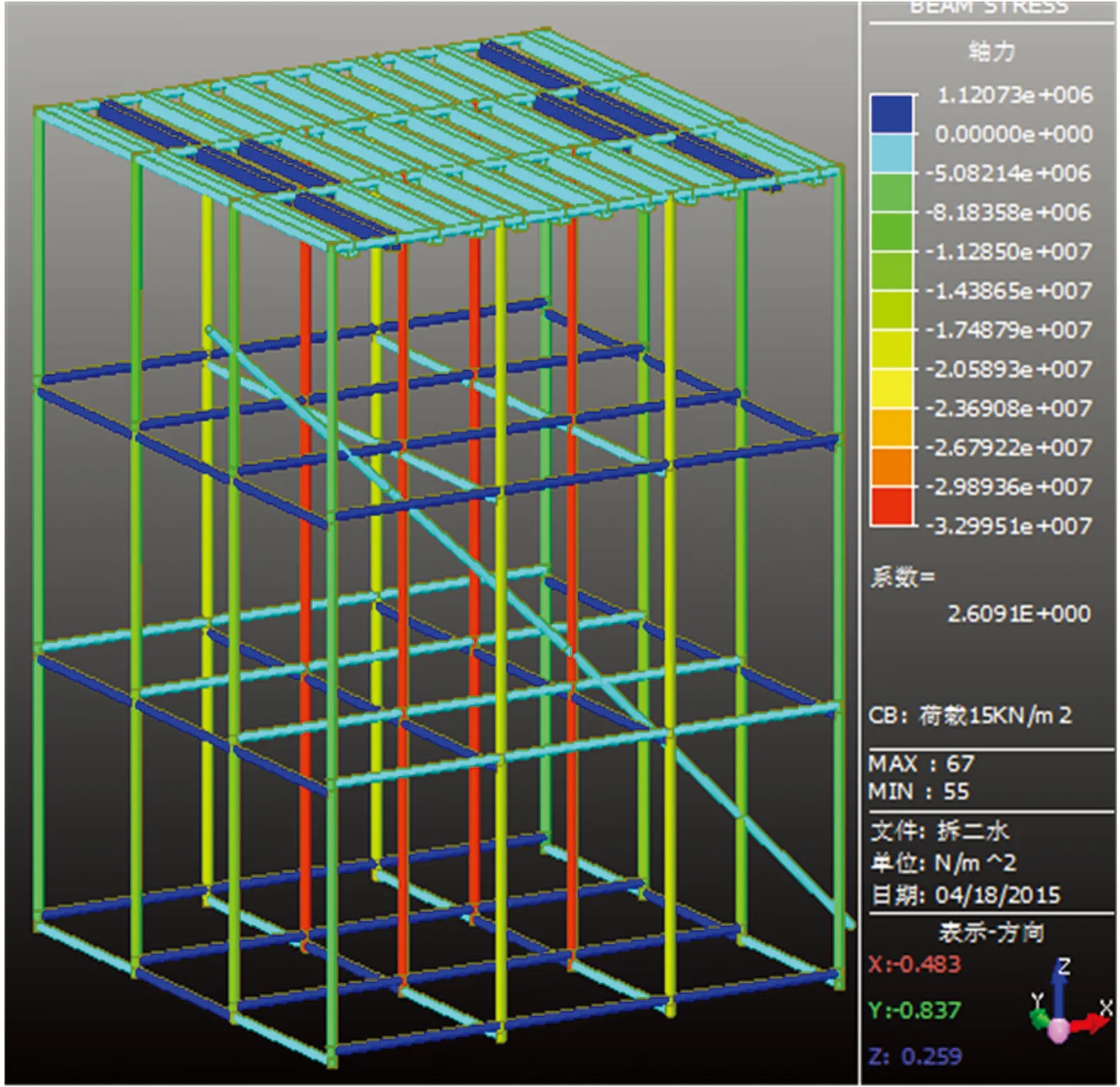
图11 拆二水条件下的杆件应力分布
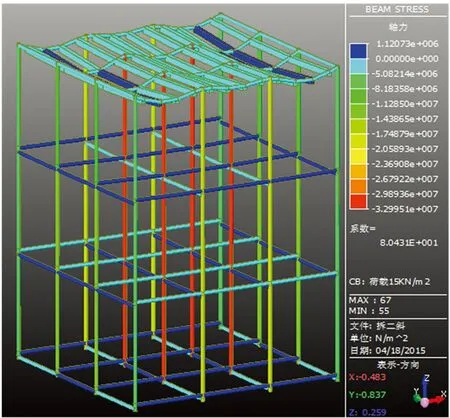
图12 拆二斜条件下的杆件应力分布
比较图8、图9 后发现,荷载达到15 kN/m2时,完整架体第三层水平剪刀撑的3段中间一段承受压应力,说明剪刀撑承担一部分应力,剪刀撑的设置提高了架体三层杆件的整体稳定性。水平剪刀撑拆除以后,架体各杆件在同等荷载作用下,内部立杆应力在减少约束的情况下,3层的各水平杆应力有所降低,说明剪刀撑的设置可以增大该层各杆件的应力值。根据表1的数据发现,荷载达到15 kN/m2时,此时拆除第三层水平剪刀撑后,各杆件应力变化不一,具体表现为:6#、11#立杆底部应力减小,7#、10#立杆应力增大,说明完整架体在拆除第三层水平剪刀撑后,6#、11#立柱在水平方向上减少1道约束,此时一部分荷载由于剪刀撑拆除,通过架体传递给7#、10#立柱, 7#、10#立杆由于应力重新分配得到一部分压应力。
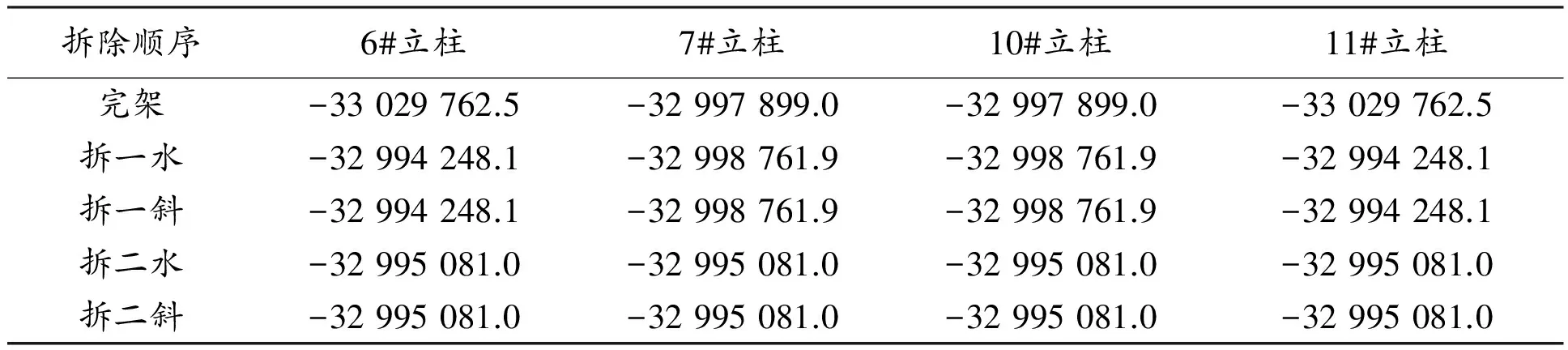
表1 架体立杆(底部)应力值 Pa
图9、图10以及表1说明1#斜撑的拆除对于整个架体受力影响较小,架体立杆底部的应力大小基本保持不变,1#斜撑对于减少架体立杆应力的传递并不起“阻碍”作用。
图10、图11显示第二层水平剪刀撑拆除后架体各杆件的应力图,7#、10#立杆在剪刀撑拆除后应力有所降低,而减小的荷载则由6#、11#立杆承担,说明水平剪刀撑的拆除会降低相邻立柱(7#、10#)应力,同时会增大周围立柱(6#、7#)应力。这个变化规律与图8、图9中的应力变化相似。图11、图12中的模型立杆应力并没有发生变化,说明2#斜撑对于架体内力的影响较小。纵观图8~图12和表1,水平剪刀撑的拆除会影响杆件应力的分布,斜撑的拆除不会影响立柱底部应力变化;综合图8~图12,虽然架体增加水平剪刀撑和斜撑,但架体立杆下部应力同时增大,说明剪刀撑的设置会增大钢管内部立杆的应力,实际工程中,并不是剪刀撑设置得越多越好。
2.2 位移变化
位移对架体的影响不可忽略,本文综合考虑扣件各节点位移对于架体的影响,观察节点处3个方向(x、y、z)位移变化对于满堂架体的影响。由于各杆件每一点位移都不一样,架体顶层位移较大,故本文采用顶层节点位移作为参考值,节点位移主要分为3个方向,即x、y、z方向(整体坐标系),节点处的3个数值分别体现3个方向上的具体位移。荷载达到最大值(15 kN/m2)架体各节点的位移值如图13~图17所示。
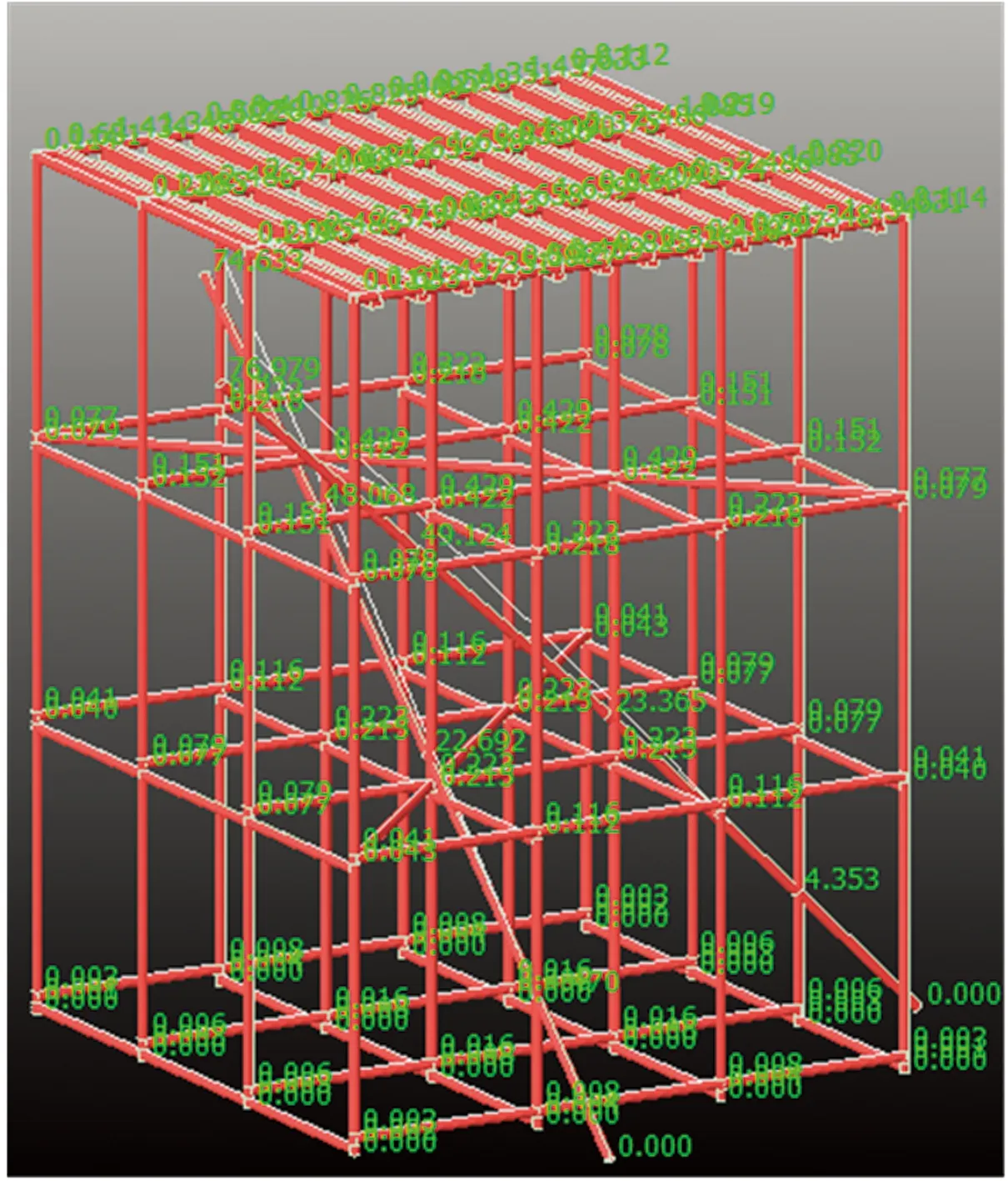
图13 完架条件下的节点位移
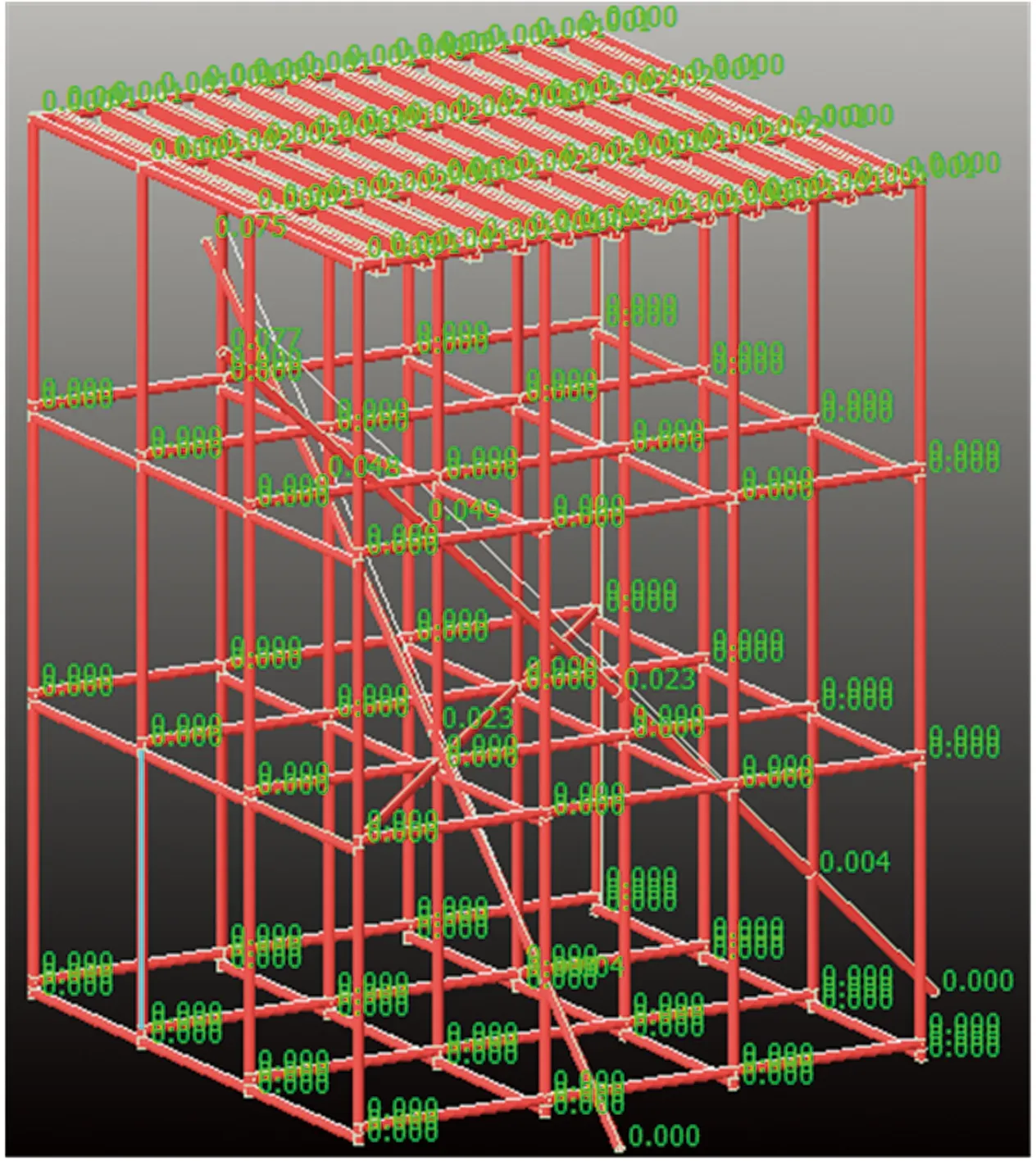
图14 拆一水条件下的节点位移
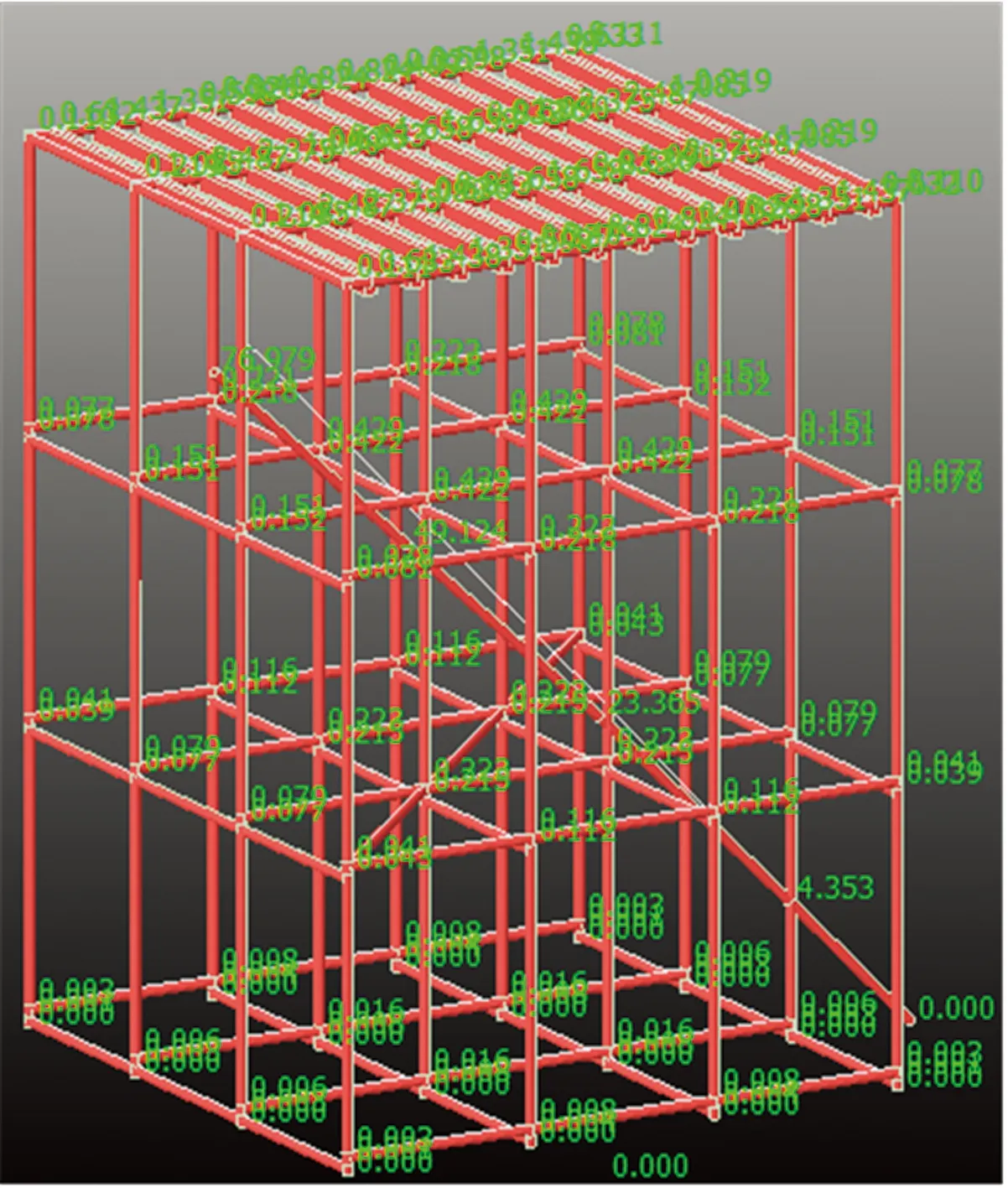
图15 拆一斜条件下的节点位移
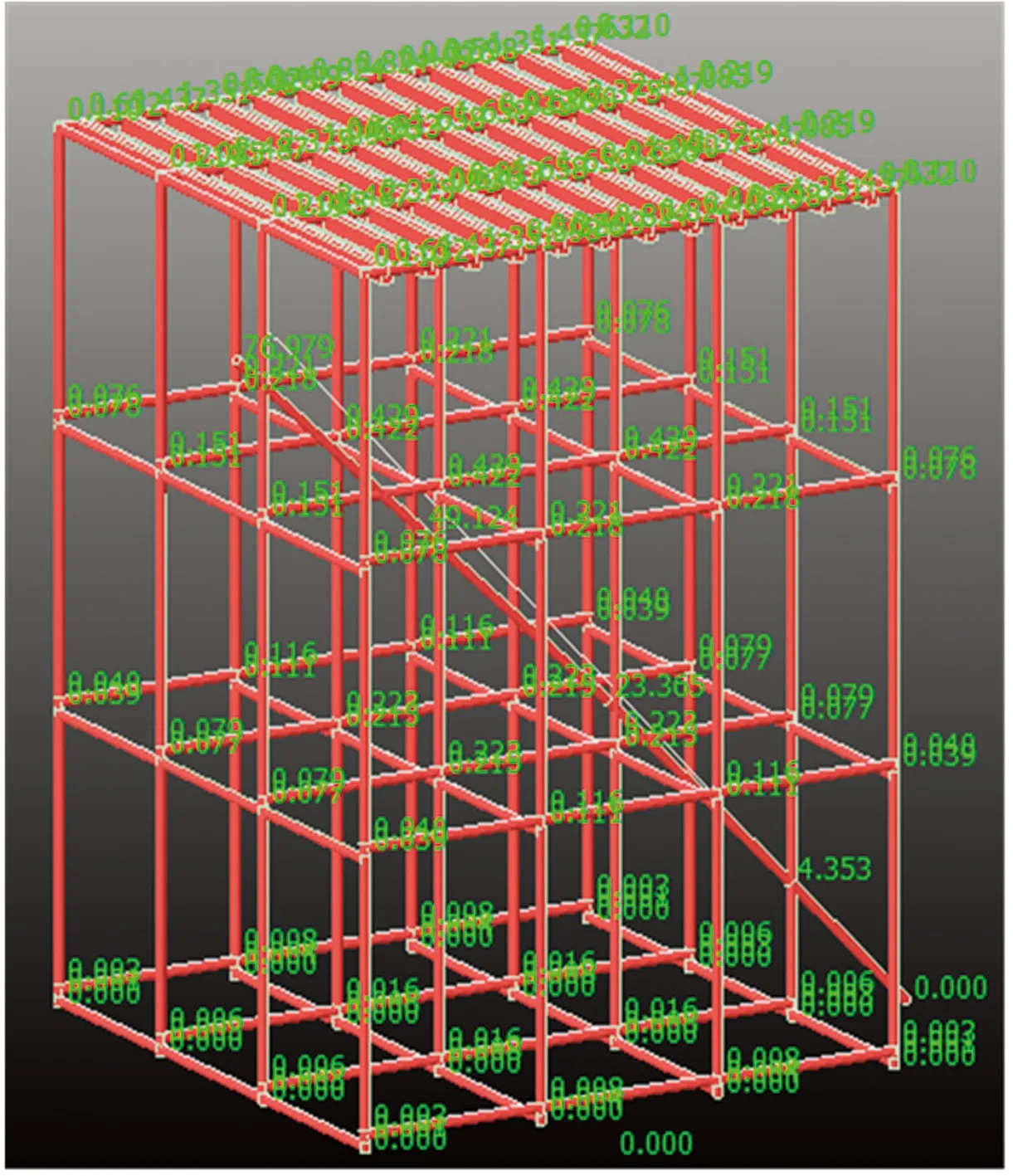
图16 拆二水条件下的节点位移
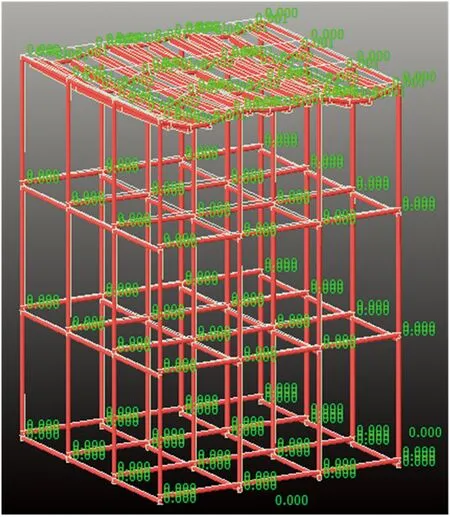
图17 拆二斜条件下的节点位移
架体顶层水平x、y、z方向的位移如表2~表4所示。由表2~表4和图13~图17发现:水平剪刀撑设置对于架体的顶层位移影响较小。完整架体三层水平剪刀撑连接1#、16#立柱,第一次拆除水平剪刀撑以后,架体的水平位移值在3个方向上基本保持不变。二层水平剪刀撑拆除后架体顶层位移也基本类似,说明水平剪刀撑的拆除对于架体顶层的位移影响较小。与此同时,在拆除1#斜撑后,架体顶层x、y方向的位移也相应变大,其中x方向的最大位移数值变化较大,局部达到0.021 mm,说明1#斜撑对于架体顶层水平方向的位移影响显著。2#斜撑拆除后,架体顶层水平位移也相应发生变化,表3说明架体在拆除2#斜撑后,在y方向的位移变化较大,局部达到0.023 mm,这说明2#斜撑对于限制架体顶层y方向的位移作用明显。
表2~表4还表明架体的顶层节点z方向有一定的位移,实际工程中应考虑其他方法进行控制。z方向的位移变化不受水平剪刀撑、斜撑的拆除而变化,说明无论是水平剪刀撑还是斜撑,其对于架体的z方向位移变化影响较小。
3 结论与展望
本文通过3×3跨的脚手架模型,研究在不同剪刀撑条件下脚手架内部杆件的应力变化情况。根据相同荷载下五种不同模型的应力变化情况,可以发现架体内部6#、7#、10#、11#立杆应力最大,2#、3#、5#、8#、9#、12#、14#、15#立杆应力次之,1#、4#、13#、16#立杆应力最小。根据试验结果可以得到:
(1)拆除一根水平剪刀撑以后,与水平剪刀撑连接的中间立杆,其应力降低,同时相邻的立杆应力增加。表1显示架体拆除一根水平剪刀撑以后,与剪刀撑连接的立杆底部应力降低0.108%,相邻立杆应力变化增加0.0091%,说明水平剪刀撑在提高架体某一层的整体刚度方面发挥着重要作用。
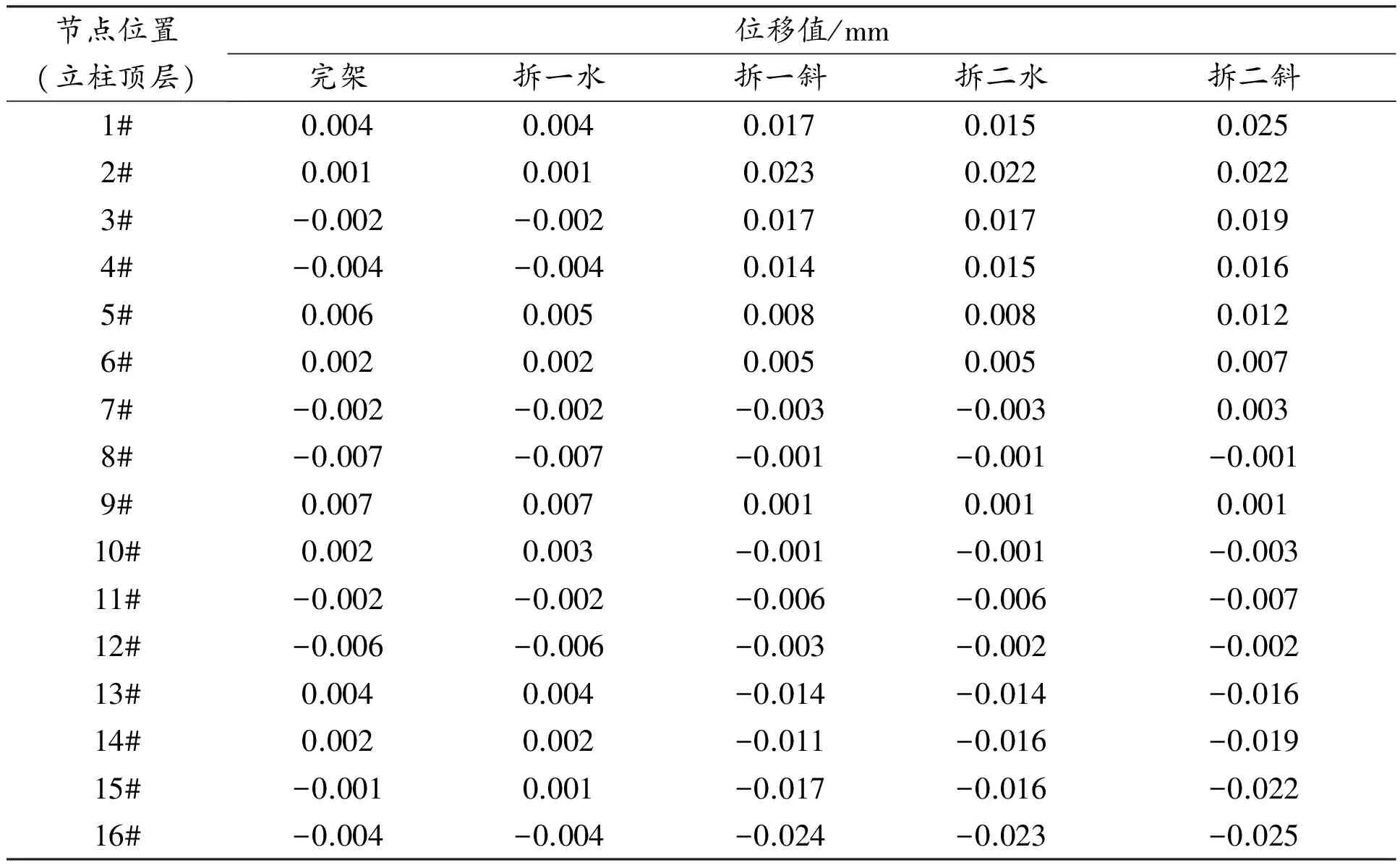
表2 架体顶层水平x方向位移(东西方向)
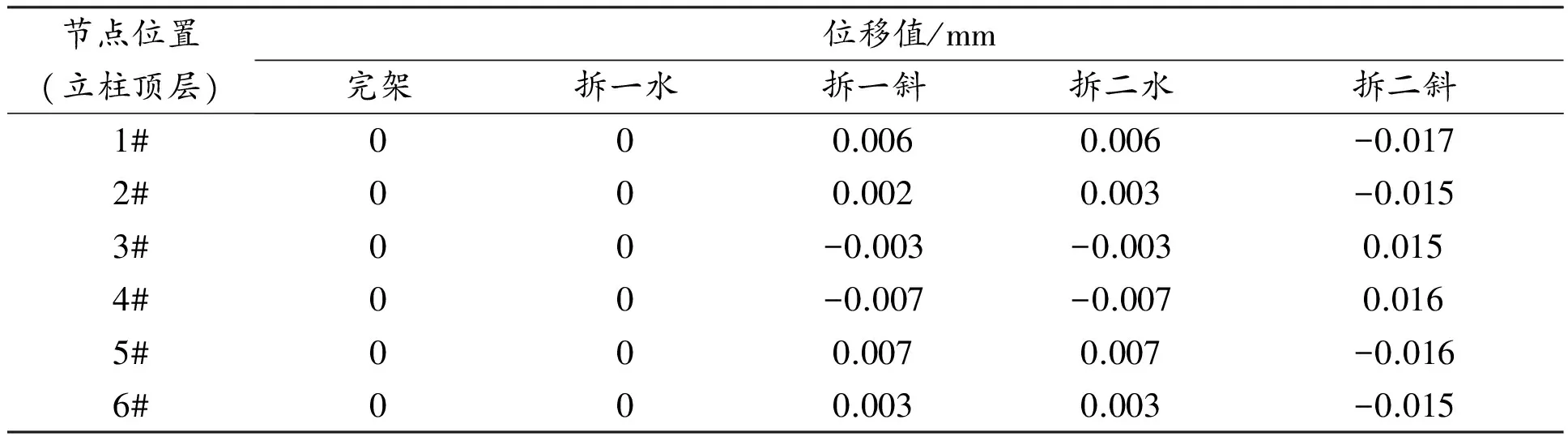
表3 架体顶层水平y方向位移(南北方向)
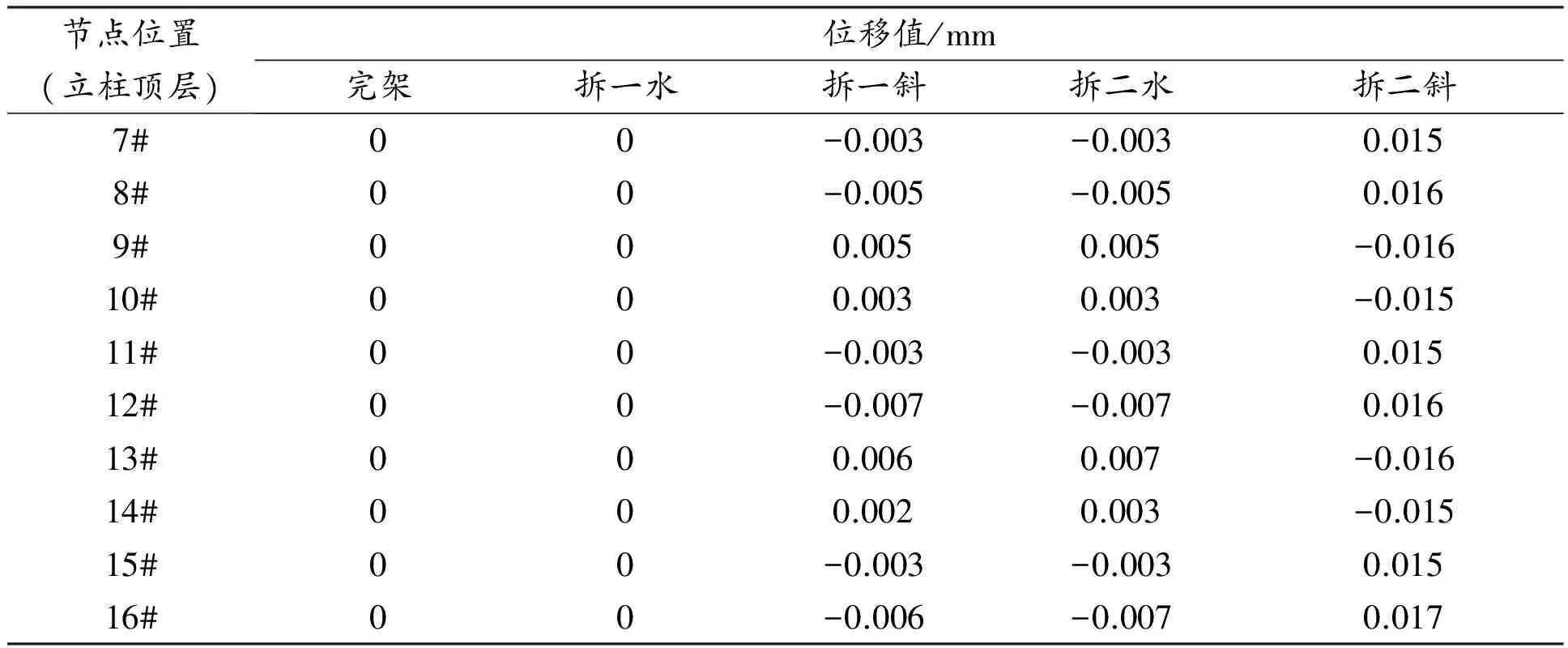
续表
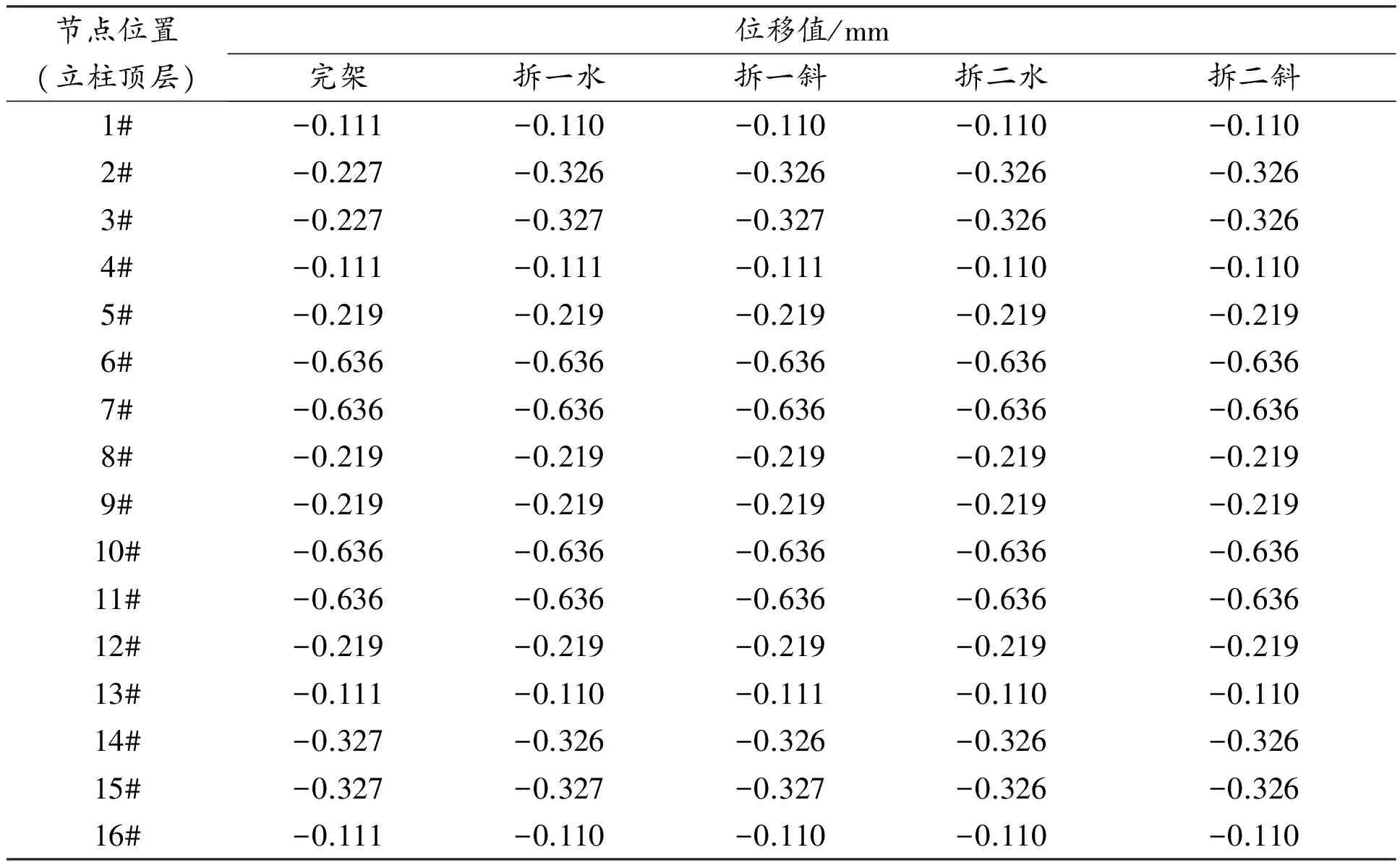
表4 架体顶层z方向位移(竖直方向)
(2)图9~图12的立杆底部应力对比表明,竖向斜撑拆除前后,钢管立柱应力基本保持不变,说明竖向斜撑的拆除对于架体内部立杆应力变化影响较小,可以忽略。
(3)该架体模型1#斜撑对于架体顶层x方向水平位移影响较为明显,而2#斜撑对于架体顶层y方向水平位移影响较为明显。
(4)表2~表4可以说明水平剪刀撑对于架体顶层的节点位移变化影响较小,除此之外,架体顶层节点z方向的位移也不受水平剪刀撑、斜撑的影响变化而变化。
通过不同模型的应力及位移模拟试验结果表明,水平剪刀撑、竖向斜撑对于提高架体的整体稳定性等方面发挥着不可替代的作用,尤其体现在水平剪刀撑对于应力传递、斜撑对于x、y位移限制等方面的影响。本文试验模拟发现,水平剪刀撑相比较斜撑,其限制应力、位移等方面作用较好;而斜撑对于限制顶层x、y水平方向位移作用明显。其次,本文试验模拟发现水平剪刀撑、斜撑对于架体顶层节点z方向位移的约束作用有限,竖向位移对于架体稳定性影响较大,关于控制架体顶层节点竖向位移需要做进一步的理论研究。实际工程可以根据不同情况设置不同的剪刀撑,最大限度地提高架体的整体稳定性,然而本文试验模拟只考虑3×3跨的简单架体,并没有模拟大面积的满堂扣件式脚手架受力过程,本文的结论和方法可以为研究大面积的满堂脚手架剪刀撑位置设置提供相应的借鉴和参考。
[1]陆征然,陈志华,王小盾,等.扣件式钢管满堂支撑体系稳定性能的有限元分析及试验研究[J]. 土木工程学报,2012,45(1):49-60.
[2]陆征然,扣件式钢管满堂支撑体系理论分析与试验研究[D]. 天津:天津大学,2010.
[3]陈志华,陆征然,王小盾,等. 基于有侧移半刚性连接框架理论的无支撑模板支架稳定承载力分析及试验研究[J]. 建筑结构学报,2010,31(12):57-63.
[4]敖鸿斐,李国强.双排扣件式钢管脚手架极限承载力分析[J]. 建筑施工,2003,25(3):214-217.
[5]建筑施工扣件式钢管脚手架安全技术规范:JGJ-130-2011[S]. 北京:中国建筑工业出版社,2011.
[6]木结构设计规范:GB 50005-2003 [S]. 北京:中国建筑工业出版社.2003.
[7]王昌兴. Midas/gen 应用实例教程及疑难解答[M]. 北京:中国建筑工业出版社,2010.
[8]北京迈达斯技术有限公司. Midas/gen 工程应用指南[M]. 北京:中国建筑工业出版社,2012.
[9]蒋玉川. MIDAS在结构计算中的应用[M]. 北京:化学工业出版社,2012.
Finite element analysis of fastener full-hall formwork scaffold in different bridging circumstances
HE Xi-ping1, LI Yang1, HE San-jun2, JI Yang-hai1,CHEN Yan1, SHAO Chuan-lin2
(1.SchoolofCivilEngineering,AnhuiJianzhuUniversity,Hefei230601,China;2.ChinaMCC17GroupCO.,LTD.,Ma’anshan243001,China)
Bridging can improve the overall stability of a bunch of the fastener full-hall formwork scaffold, it can strengthen the scaffold connection in areas such as the vertical and horizontal pole and play an important role in load transferring. In this paper, set up a 3x3 fastener full-hall formwork scaffold model by using MIDAS/GEN software to get the changing rules of stress and displacements of the scaffolding upright stanchion in different bridging circumstances and the same loads. The results can be used as a reference for studying the rules of stress transferring of the fastener full-hall formwork scaffold in practical engineering to make the correct position of the horizontal and sloping diagonal bracing.
fastener full-hall formwork scaffold; bridging; stress; displacement; rigid model
2015-07-15
安徽省教育厅高等教育振兴计划(2013zdjy121);安徽省教育厅质量工程项目(2014gxk063);安徽省科技攻关计划项目(1501041133)
何夕平(1963-),男,安徽无为人,硕士,教授,硕士生导师。
1674-7046(2015)05-0022-08
10.14140/j.cnki.hncjxb.2015.05.005
TU731.2
A

