引洮7#隧洞TBM开挖与管片衬砌支护过程的三维数值分析

赵永众

(甘肃省白银市水电勘测设计院，甘肃 白银 730900)



引洮7#隧洞TBM开挖与管片衬砌支护过程的三维数值分析

赵永众

(甘肃省白银市水电勘测设计院，甘肃 白银 730900)

结合引洮供水工程资料，采用有限元D-P屈服准则和ANSYS软件中的单元“生死”技术对隧洞的开挖和管片衬砌支护过程进行三维数值模拟。分析了开挖前后围岩的应力与变形情况、开挖不同阶段围岩的应力与变形和管片衬砌的等效应力情况。分析表明，开挖过程中围岩和管片应力与变形随开挖时间和空间不断变化，初始围岩应力对隧洞围岩和管片的应力与变形的影响较大，这为今后管片设计和隧洞施工提供了数据参考和依据。

单护盾TBM；D-P准则；“生死”技术；隧洞开挖；数值模拟

1 工程概况

引洮7#隧洞工程区位于甘肃省定西市渭源县境内，是甘肃省引洮供水一期工程的标志性工程。隧洞总长度17.286 km，设计断面为圆形，管片衬砌后内径为4.96 m。该隧洞洞段大部分为Ⅴ类围岩，岩性极差，岩性主要由白垩系K1hk3、上第三系N2L3及白垩系K1hk4的岩层构成，属软岩-极软岩，洞段内裂隙较发育且有基岩裂隙水，个别洞段地下水相应较大，整个洞段围岩极不稳定，不能自稳。本文工程在TBM施工过程中多次出现掌子面坍塌、隧洞涌沙、TBM“栽头”等不良地质情况。因此，进行TBM开挖与管片衬砌的三维数值模拟分析，研究开挖衬砌过程中围岩和管片的应力变形情况，具有重要的意义[1]。

2 管片衬砌有限元分析理论

2.1 单元生死属性

ANSYS中单元“生死”不是生成新的单元，也不是将单元从模型中删除。而是通过设置单元的阻尼、质量、比热容和其他参数的大小来体现单元的生与死；将单元“杀死”时，其各个参数值设置为0，单元“出生”是重新激活单元的同时，恢复其各个参数的值。

TBM隧洞开挖时，为了更好地模拟管片衬砌与围岩的相互作用，可用ANSYS程序直接选择将被挖掉的单元，然后将其“杀死”，从而实现开挖的模拟。

2.2 Drucker-Prager准则

弹塑性有限元分析中，Mohr-coulomb准则计算上存在困难，大都采用Drucker-Prager屈服准则。Mohr-coulomb强度准则的破坏曲面为不规则的六角锥面，在棱边转角处数学处理困难。因此，Drucker和Prager对其提出修正，建议用一个正圆锥面代替上述不规则的六角锥面，他们提出的准则称为Drucker-Prager准则。

Drucker-Prager屈服准则表达式为

(1)

式中I1、J2分别为应力张量第一不变量和应力偏量第二不变量，即

I1=σ1+σ2+σ3=σx+σy+σz

(2)

(3)

α、k是材料试验常数，在平面应变状态下为

(4)

(5)

Drucker-Prager强度准则反映了中间主应力的影响，考虑了静水压力的作用，且具有完美的数学表达式，因而得到了广泛的应用。

3 建立有限元模型

在进行隧洞开挖与管片衬砌过程的三维数值分析时[2]，采用Solid45单元来模拟围岩结构，SHEIL63单元模拟管片衬砌结构，选用D-P准则进行围岩的有限元弹塑性分析。采用Mesh200单元建立管片衬砌结构的线模型和土体的面模型，然后拉线模型成壳模型，将面模型拉伸为体模型。TBM掘进时，利用单元“生死”技术模拟TBM的开挖过程，同时分析管片衬砌上的受力情况。

3.1 计算范围和边界条件

图1 有限元模型

隧洞开挖后，周围岩体中应力重分布的范围是有限的[3]。根据取值原则，以隧洞的洞心为原点，水平方向和竖直方向均取20 m范围内的岩体，沿水流方向取50 m范围内的岩体为研究对象，建立的有限元模型如图1所示。

模型的边界约束条件包括位移边界条件和应力边界条件[4]。位移约束条件通常是在计算范围内的岩体前后左右加水平约束，底部加全约束，应力边界条件为上部考虑300 m岩石重力所产生的垂直压力，同时考虑岩体本身的自重。

3.2 材料参数

围岩和衬砌管片的材料参数如表1所示。

表1 管片结构计算参数表

用普适法计算围岩压力，得到的结果如表2所示。

对于松散岩体地层TBM施工时，围岩的抗力系数很小，可忽略地基反力对管片衬砌的作用，同时，施工工序复杂，暂不考虑施工荷载对管片的影响。因此，管片所受的主要荷载是围岩压力和管片自重，根据工程经验，管片重度取值为26.5 kN/m3[5]。

表2 普氏法计算结果表

4 隧洞开挖过程ANSYS数值分析

4.1 V类岩体隧洞开挖前后围岩应力变形情况

(1)隧洞开挖前围岩应力变形情况。

在隧洞开挖前，结构为一整岩体，岩体仅受重力作用，并在其自身重力作用下产生初始地应力，并在Y方向产生变形，最大变形量为43.914 mm。

图2 开挖前重力作用下隧洞竖向应力图(单位：Pa)

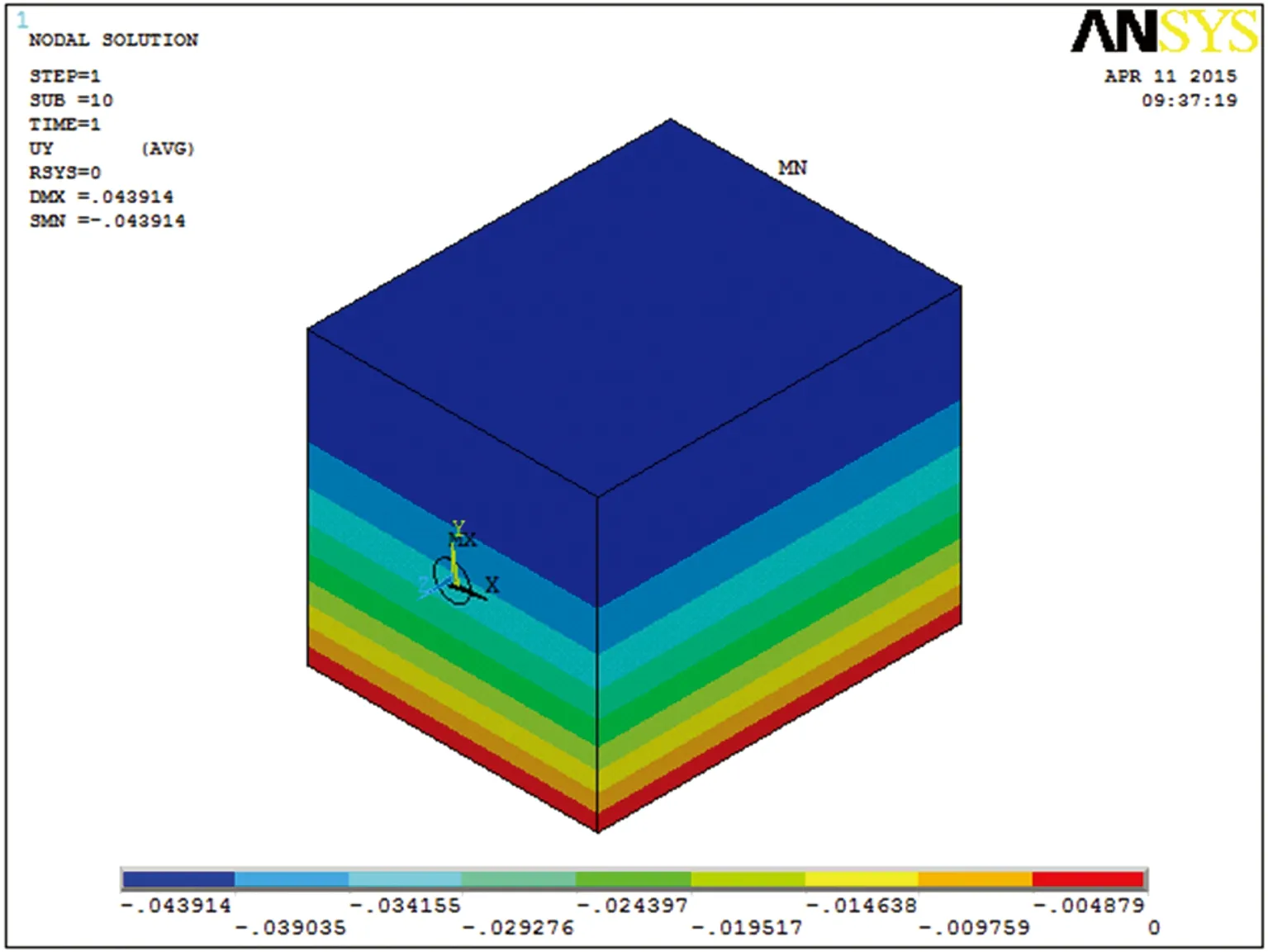
图3 开挖前重力作用下隧洞Y方向变形图(单位：m)

(2)隧洞开挖后围岩应力变形情况。

由应力变形云图可以看出，TBM隧洞开挖后，由于初始围岩压力作用致使隧洞应力重新分布，受其应力重分布的影响，围岩的变形呈现出隧洞顶部下沉，两侧向隧洞轴心收敛，底部向上拱起的趋势，其中竖向最大变形量为46.061 mm。开挖面洞壁变形情况与管片环变形情况一致，呈近似椭圆形，竖直方向变形大于水平方向，均指向隧洞轴心，这是因为深埋隧洞开挖时的围岩压力远大于管片产生的抗力，所以管片抗力对洞壁变形的作用几乎不考虑，故二者的变形方式相同。

图4 开挖后隧洞竖向应力图(单位：Pa)

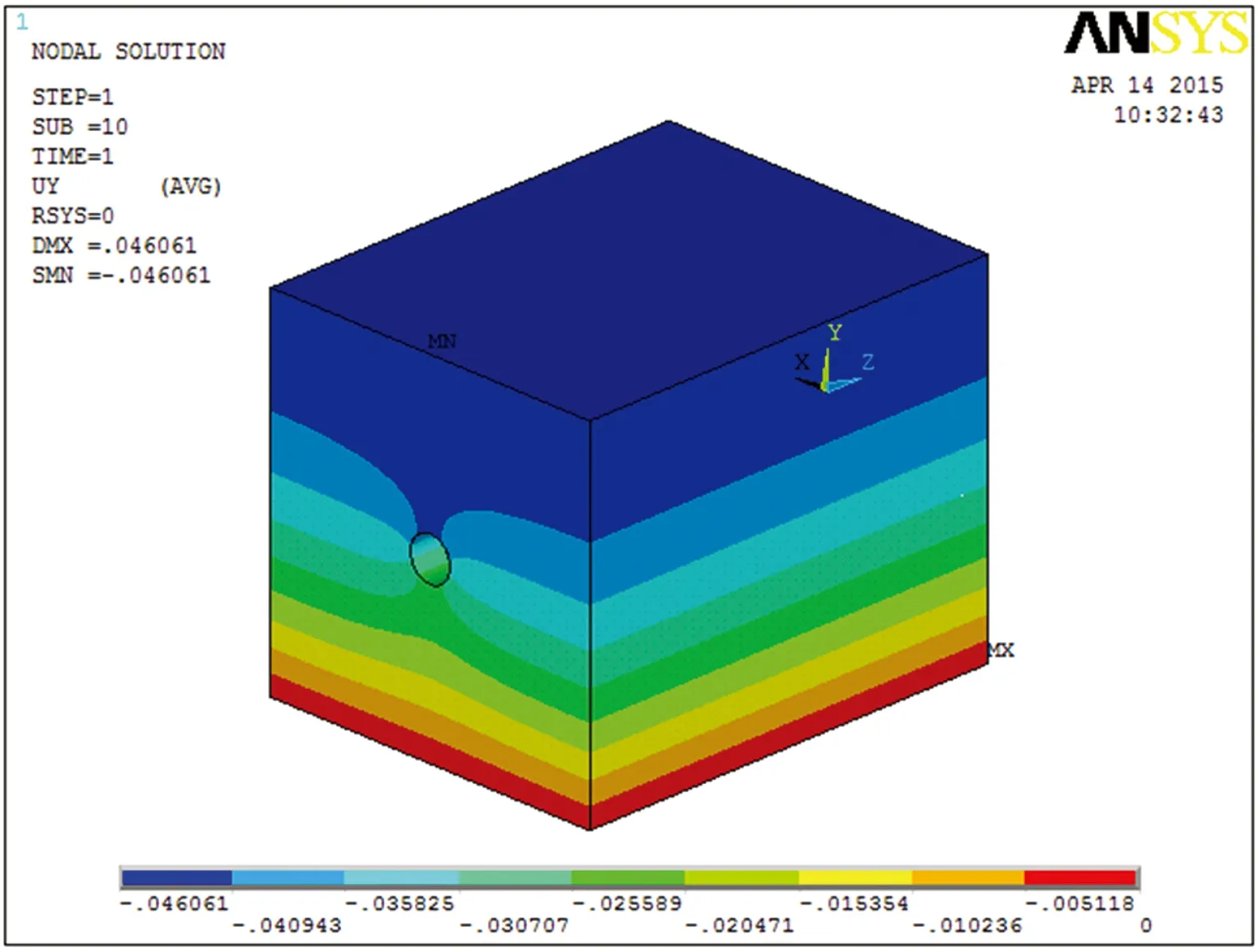
图5 开挖后隧洞Y方向变形图(单位：m)

4.2 隧洞开挖过程数值模拟

4.2.1 开挖过程围岩变形规律

TBM隧洞开挖过程的数值模拟，目的在于研究TBM隧洞在推进过程中围岩和管片衬砌的受力变形情况，有助于把握开挖各个阶段及运营期围岩的稳定性和隧洞的受力变形情况，也有助于分析各个开挖阶段衬砌管片的受力情况。假定TBM隧洞开挖后，随即进行管片安装。计算时，施工过程基于简化假设：每次开挖5 m，分10次完成。具体操作是：

①先把每次挖去的岩体单元选择为有效单元，将其“杀死”，不显示其属性；

②选择所挖去岩体部分对应的管片单元为当前有效单元，将其激活并删除其节点上的约束；

③选择刚被激活的管片单元和未挖去的岩体单元；

④反向选择，约束死单元所有节点上的自由度。

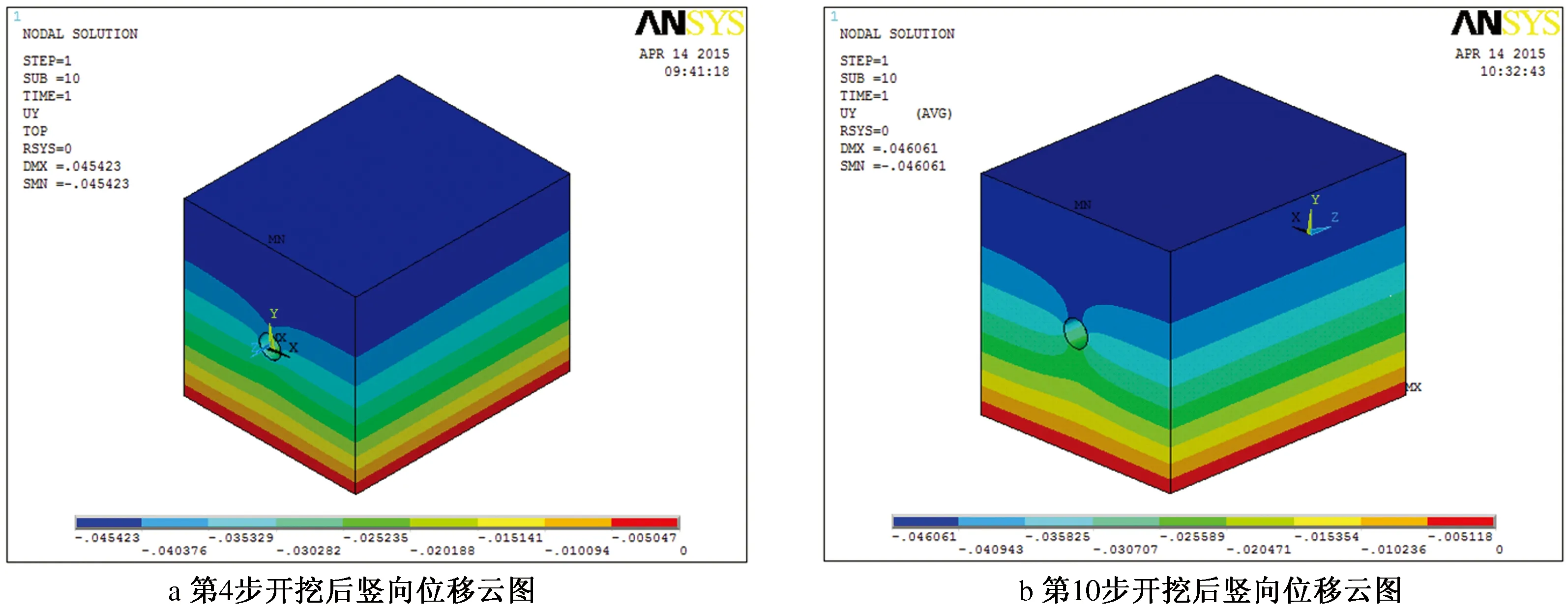
图6 开挖后围岩竖向位移云图 (单位：m)

(1)围岩竖向(y向)变形情况。

图7 隧洞顶部变化量特征值(单位：m)

从变形规律可以看出，随着TBM推进，地层竖向(y向)变形的范围逐步扩展，隧洞顶部沉降量和洞底拱起量在逐渐增加且变形明显，可以看出，掘进时隧洞顶部影响范围的扩展速度比隧洞底部快，岩体最大变化量特征值出现在洞顶附近，由图7可以看出，TBM掘进中岩体最大变化量特征值刚开始变化幅度较大，后渐渐缓慢并趋于稳定，这说明开挖前期由于围岩压力作用岩体沉降量大，开挖过程中应力释放，使岩体下沉量减小并趋于稳定，隧洞顶部的最大下沉量为46.061 mm。顶部变化量特征值的变换规律见表3所示。

表3 隧洞顶部变化量特征值

(2)围岩横向(x向)变形情况。

从图8可以看出：TBM开挖过程中，地层围岩总的移动趋势是洞顶下沉、洞底向上拱起、管片左右两侧岩体呈张开趋势。随着开挖的进行，横向变形范围逐渐扩大，开挖后围岩横向最大位移值为2.322 mm，主要集中在隧洞断面水平方向45°左右附近。

(3)x=5 m处开挖引起岩体竖向变形情况。

由TBM掘进过程中x=5 m处围岩的纵向变形图可以看出：TBM开挖初期，在TBM开挖区域形成一个临空面(图9中红色区域)，致使开挖后周围岩体有向凌空面变形的趋势，变形趋势为临空面顶部岩体下沉而底部拱起，距开挖面较远处变形较小(见图9)。随着TBM的掘进，引起岩体纵向变形的范围向上向下扩展变大，上部的扩展速度大于下部的拱起速度，岩体总变形趋势随着临空面的前进而向前推进。开挖结束后，围岩纵向变形达到最大，最大变形量出现在临空面上部附近，最大值为46.986 mm。

图8 开挖后x方向位移云图(单位：m)

图9 x=5 m处开挖引起岩体纵向变形图(单位：m)

4.2.2 管片环应力分析

TBM开挖时，假定完成开挖立即进行管片安装，通过单元“生死”技术来模拟管片应力变形属性。开挖过程中，通过“杀死”开挖岩体单元的同时“激活”管片单元，被“杀死”单元的质量、刚度等参数值均为0，只体现管片单元的属性，从而实现管片的安装过程(见图10)。

图10 开挖后管片应力云图(单位：m)

TBM掘进过程中，由于围岩压力作用，管片环开始受压，管片环应力随TBM掘进而发生变化。最初管片所受的围岩压力较大，掘进中由于初始围岩应力释放而趋于稳定。由图10可知，管片腰部应力等值线较密集，所受应力较大，且管片内侧应力大于外侧应力，此处管片易受压破裂；顶部和底部相对较小，其分布则是外侧应力大于内侧应力值，TBM开挖完成后管片等效应力为9.72 MPa，满足钢筋砼抗压要求。

由表4、表5和图11可知，管片变形情况与围岩变形情况相似，管片顶部(A点)的纵向变形量较管片两侧(B点)变形量大，变形后隧洞断面呈近似椭圆形状，变形趋势均为开挖前期较大，后期变形量趋于稳定。管片顶部A点最大下沉量为39.558 mm，B点最大变形量为36.012 mm。

表4 隧洞顶点A点变化变化量特征值

表5 隧洞水平方向B点变化变化量特征值

图11 隧洞A、B点变化量特征值比较

5 结论

(1)TBM隧洞开挖和管片衬砌过程中，初始围岩压力对隧洞围岩和管片应力变形影响很大，施工过程中不能忽视，应采取相应的加固措施，防止隧洞坍塌，初始应力达到稳定后，隧洞变形趋势趋于稳定。

(2)TBM开挖过程中，围岩在竖向、横向和纵向都随着TBM的推进而不断变化，三维有限元所得到的变形规律与工程实际情况较为吻合，这为本工程及以后工程设计施工提供了依据。同时，TBM向前掘进也使管片应力、变形不断发生变化，管片等效应力分析可以为管片设计和安装进行指导，防止因设计和安装不当使管片发生破裂，影响隧洞的过水能力。

[1]李围. ANSYS土木工程应用实例[M].北京.中国水利水电出版社,2007.

[2]李鹏涛.TBM施工隧洞衬砌管片内力分析模型研究[D].杨凌：西北农林科技大学,2009.

[3]王惠德,冯家聪,范家齐.弹性力学解析法与数值法[M].哈尔滨:哈尔滨工业大学出版社，1987.

[4]熊开智.深埋盾构隧洞装配式管片衬砌设计中的数值方法研究[M].天津：天津大学.

[5]周太全,华渊,汪仁和,等.软弱围岩隧道施工全过程非线性有限元分析[J].岩土力学,2004.25(2):338-342.

Yintao 7# tunnel TBM excavation and segment lining and supporting process three-dimensional numerical analysis

ZHAO Yong-zhong

(GansuBaiyinHydropowerSurvey&DesignInstitute，Baiyin730900,China)

Combining Yintao water supply project7# tunnel, using D-P yield and ANSYS software of the unit “birth and death” technology for tunnel excavation and segment lining and supporting process 3-d numerical simulation to analyze the stress and deformation of the surrounding rock before and after the excavation, at different stages of surrounding rock stress and deformation and Von Mises of the segment lining. Analysis shows that the deformation and stress of surrounding rock and lining segments in the process of excavation with the excavation space and time changing, stress of initial rock stress of surrounding rock and lining segments change are bigger, the segment design and tunnel construction provide the data for the future reference and basis.

single shield TBM; drucker-prager yield criterion; "birth and death" technology; excavation of tunnel; numerical simulation

2015-07-29

赵永众(1978-)，男，甘肃白银人，工程师。

1674-7046(2015)05-0030-06

10.14140/j.cnki.hncjxb.2015.05.006

TV554

A