一种测量介质损耗角的卷积窗加权算法
历 伟,常 宽
(沈阳工业大学 电气工程学院,辽宁 沈阳 110870)
一种测量介质损耗角的卷积窗加权算法
历 伟,常 宽
(沈阳工业大学 电气工程学院,辽宁 沈阳 110870)
目前,谐波分析法在高压容性设备介质损耗角的在线测量中得到了广泛的应用,但是该方法在非同步采样时存在频谱泄漏,严重影响介质损耗角的测量精度。分析了Blackman自卷积窗的频谱特性,提出了基于Blackman自卷积窗双谱线插值FFT的介质损耗角测量算法,并详细推导了介质损耗角的计算公式,最后利用计算机进行仿真验证,结果表明该算法能有效提高介质损耗角的测量精度。
介质损耗角;谐波分析法;Blackman自卷积窗;插值FFT;测量精度
介质损耗角是一个能够表征高压容性设备绝缘状况的重要参数,历来受到设备维护人员的重视。高精度的介质损耗角的测量方法具有重要的现实意义。目前,介质损耗角的测量方法可分为硬件法[1-2]和软件法[2]。硬件法对硬件条件要求较高,而且易受测量系统及外部环境的影响,测量误差较大。以谐波分析法为代表的软件测量方法具有抗干扰性好、易实现、精度高等优点,得到了国内外科研人员深入、广泛的应用研究,然而在非同步采样时,谐波分析法存在频谱泄露和栅栏效应,严重影响了介质损耗角的测量精度。为提高测量精度,文献[3]提出了加Hanning窗加权插值FFT算法,文献[4]提出了加Blackman-Harris窗插值算法,文献[5]提出了介质损耗角的卷积窗加权算法,这些算法都有效地提高了介质损耗角的测量精度。
本文对Blackman自卷积窗的频谱特性进行了研究,提出利用Blackman自卷积窗加权,并采用双谱线插值算法测量介质损耗角,利用曲线拟合求得频谱校正偏差,并推导出了该算法下介质损耗角的计算公式,最后利用计算机分别对信号基波频率波动、谐波含量和白噪声的干扰进行了仿真验证。
1 Blackman自卷积窗的特性
为抑制窗函数频谱泄露,在已有理论的基础上,本文对Blackman自卷积窗进行分析研究,并运用在介质损耗角的测量中。作为广义余弦窗的一种,Blackman窗函数离散时域的表达式为
(1)
其频域表达式为
(2)
式中WR(ω)为矩形窗函数的幅频特性函数。
Blackman自卷积窗是由p个长度为N的Blackman窗w(k)进行自卷积分运算得到的,其中p为阶数,通常为方便计算,对卷积分运算后的序列在其首部或尾部进行补零,使得p阶自卷积窗长度为pN。由卷积定理可知,p阶Blackman自卷积窗的表达式为
(3)
图1为Blackman多阶自卷积窗的幅频曲线,可以看出,随着卷积阶数的增加,窗函数的旁瓣峰值电平逐渐减小,旁瓣衰减速率逐渐增大,窗函数特性到了明显的改善,显然更能有效地抑制频谱泄露。

图1 1~4阶Blackman自卷积窗幅频曲线
2 Blackman自卷积窗加权双谱线插值FFT算法分析
为分析方便,不失一般性,以基波时域信号为例:
x(t)=A0sin(2πf0t+φ0)
(4)
式中:A0、f0、φ0分别表示基波的幅值、频率、初相角。设以满足Nyquist定理的采样频率f0对信号x(t)采样,得到的离散序列为
(5)
对离散序列x(n)进行加Blackman自卷积窗处理,并忽略傅里叶变换后的负频率影响[6],可得到加Blackman自卷积窗后的DFT变换式:
(6)
式中:WP(k)为p阶Blackman自卷积窗频谱函数,k=1,2,…,L-1;k0=f0L/fs。
同步采样时,k0为整数,即基波频率刚好落在采样频点上,而非同步采样时,由于栅栏效应,k0不是整数,而采样点数是整数,这就造成了误差,为提高测量精度,必须对谱线进行校正,以找出更准确的谱线。频谱校正方法有能量重心法、相位差法、比值法等。本文采用文献[6]中的双频谱插值法对频谱进行校正。

(7)
式(7)是λ=f(d)的函数。若能利用反函数求出d,即可求出校正后的频谱参数,然而考虑到Blackman自卷积窗函数的复杂性,求反函数比较困难,可以利用曲线拟合函数polyfit(λ,d,m)求得拟合多项式系数,进而求得λ= (a1-a2)/(a1+a2) 时对应的d,其中m为拟合的阶数,m越大求得的d越准确。考虑到算法的实时性,此处取m=7,采用2阶Blackman自卷积窗时得到的插值逼近式为
d=0.049 5λ7+0.074 3λ5+0.152 77λ3+ 1.96λ
(8)
根据式(8)和λ=(a1-a2)/(a1+a2)可以求得变量d,进而可求得基波频率修正公式:
(9)
基波相位校正公式为
(10)
根据式(10)可分别求出电压基波初相位φu0和电流基波初相位φi0,所以介质损耗角δ为
(11)
3 计算机仿真分析
为验证上述算法的有效性,本文采用了文献[7]中的信号模型,即含有奇次谐波的电压、电流的模拟信号:
(12)
(13)
式中:Uh和Ih分别为第h次谐波的电压幅值和电流幅值;δh为第h次谐波下的介质损耗角值;fh为第h次谐波的频率。计算机仿真时,本文通过改变基波频率f1的值来验证该算法对频率波动的抗干扰能力,以及通过改变谐波含量来验证该算法对谐波的抗干扰能力。
3.1 基波频率波动对介质损耗角测量的影响
考虑到实际电网频率的波动,仿真时基波频率f1依次为49.5 Hz、49.8 Hz、50.0 Hz、50.3 Hz、50.5 Hz,取频率为1 kHz,采样点数L=1 024,对应测出的介质损耗角的相对误差如表1所示。由表1可以看出,加2阶Blackman自卷积窗在频率波动时介质损耗角的最大测量相对误差不超过2.35×10-5%,相对于加Blackman窗时精度提高了4~5个数量级,满足介质损耗角的测量要求。
3.2 谐波含量对介质损耗角测量的影响
为仿真谐波含量对介质损耗角测量的影响,保持基波信号频率为50.3 Hz不变,信号包含的3次谐波量由0%逐渐变化到25%,得到的测量结果如表1所示。从表1可以看出,采用2阶Blackman自卷积窗时,介质损耗角的相对测量误差最大不超过2.476×10-5%,而且随着谐波含量的增加,相对误差的波动很小,可以看出该算法对谐波的抗干扰效果很好。
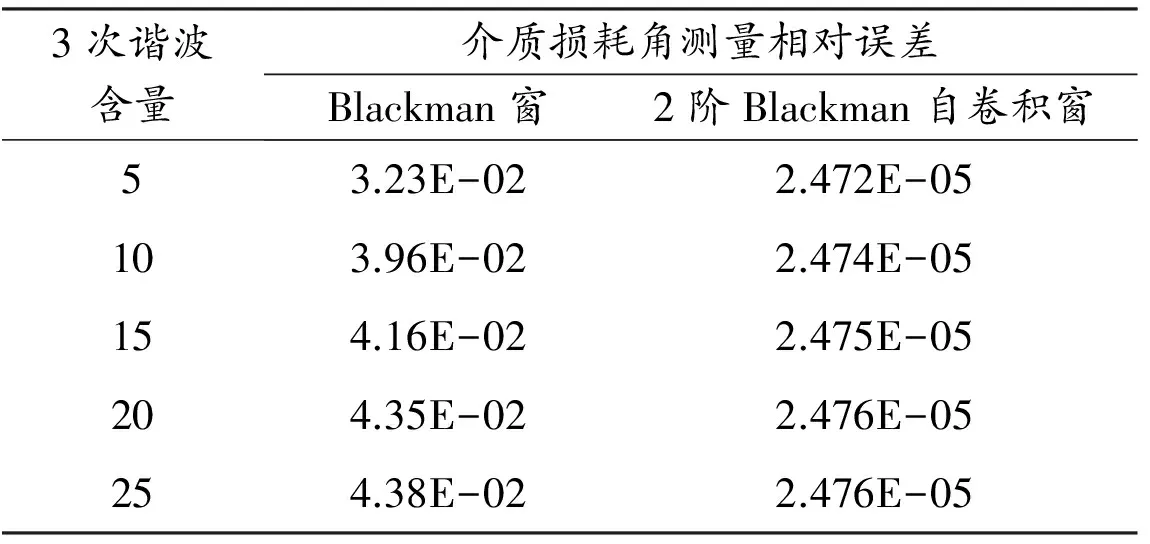
表1 频率波动对介质损耗角测量的影响 %
3.3 白噪声对介质损耗角测量的影响
在模拟信号中加入白噪声,信噪比依次为10 dB、20 dB、30 dB、40 dB、50 dB、60 dB,测得的介质损耗角相对误差如表2所示。从表2可以看出,随着信噪比的增加,测量误差逐渐减少,2阶Blackman自卷积窗在20 dB以下时,白噪声严重影响介质损耗角的测量,但是信噪比高于或等于20 dB时,最大的测量相对误差低于2.678×10-3%,此时已经满足测量精度要求,所以该算法对白噪声有较好的抑制效果,但是在现场应用中白噪声较大时,需要对信号进行消噪处理。

表2 白噪声对介质损耗角测量的影响
4 结束语
针对非同步采样时谐波分析法存在的泄露效应和栅栏效应,提出采用加Blackman卷积窗加权算法,利用双谱线插值法进行频谱校正。计算机仿真结果表明:该算法对频率波动、谐波干扰、白噪声干扰有很好的抑制效果,有效提高了介质损耗角的测量精度。
[1]蔡国雄,胡兆明,王建民.介质损耗测量的过零点电压比较法[J].电网技术,1995,19(10):1-5.
[2]律方成,晁红军,徐志钮,等.介损角数字化测量综述[J].华北电力大学学报,2008,35(6):21-26.
[3]柴旭峥,关根志,文习山,等.tanδ高准确度 测量的加权插值FFT算法[J].高电压技术,2003,29(2):32-33.
[4]王楠,律方成,梁英,等.基于高精度DFT的介损数字测量方法[J].高电压技术,2003,29(4):3-8.
[5]张介秋,梁昌洪,韩峰岩,等.介质损耗因数的卷积窗加权算法[J].电工技术学报,2005,20(3):100-104.
[6]温和,滕召胜,王永,等.频谱泄漏抑制与改进介损角测量算法研究[J].仪器仪表学报,2011,9(32):2087-2094.
[7]万全,高云鹏,罗志坤,等.基于Nuttall窗频谱校正的介质损耗因数测量[J].仪器仪表学报,2010,31(1):15-20.
[8]徐志钮,律方成,赵丽娟.基于加汉宁窗插值的谐波分析法用于介损角测量的分析[J].电力系统自动化,2006,30(2):81-85.
[9]孙鹏,杨永越,刘黎明,等.基于Hanning卷积窗的DFT介质损耗角测量算法[J].电测与仪表,2014,51(16):73-77.
[10]徐志钮,律方成,罗运国,等.介损角测量的两种加窗插值DF T算法[J].华北电力大学学报,2006. 33(5):11-14,24.
[11]王微乐,李福棋,谈克雄.测量介质损耗角的高阶正弦拟合算法[J].清华大学学报(自然科学版),2001,41(9):5-8.
[12]高云鹏,滕召胜,温和,等.凯塞窗插值FFT的电力谐波分析与应用[J].中国电机工程学报,2010,30(4):43-48.
Convolution window weighted algorithm of dielectric loss angle measurement
LI Wei, CHANG Kuan
(SchoolofElectricalEngineering,ShenyangUniversityofTechnology,Shenyang110870,China)
Harmonic analysis method is widely used to measurement of dielectric loss angle of high voltage capacitive equipment, however, this method has spectral leakage when non synchronous sampling and seriously affect the measurement accuracy of dielectric loss angle. In order to restrain the error, many academics have proposed many effective improved harmonic analysis methods. This paper analyzed the Blackman Self-convolution spectral characteristics, and proposed a double spectrum line interpolation FFT algorithm with Blackman convolution window, and deduced the formula for calculating the dielectric loss angle in detail. Finally, through computer simulation, the results showed that the Algorithm can improve the accuracy of measurement effectively.
dielectric loss angle; Harmonic analysis method; Blackman self-convolution; interpolation FFT; accuracy of measurement
2015-07-07
厉 伟(1962-),男,辽宁沈阳人,博士,教授。
1674-7046(2015)05-0072-04
10.14140/j.cnki.hncjxb.2015.05.014
TM835.4
A

