从非周期信号的FT到周期信号的FS

宫二玲，孙志强，刘亚东

(国防科学技术大学机电工程与自动化学院，湖南长沙 410073)

0 引言

“信号与系统”课程是国内外高校电子信息类、控制类、计算机类等专业的基础课程，它以“高等数学”、“电路分析”等前期课程为基础，本身又是后续的“数字信号处理”、“通信原理”和“自动控制原理”等课程的基础，在教学环节中起着承上启下的作用。傅里叶分析是该课程一个非常重要的部分，经典教材中讲授该部分时，一般都是按照历史上对该问题的研究顺序展开的，即先介绍周期信号的傅里叶级数展开，然后将周期信号的周期无限扩大，在时域上将其演变为非周期信号，同时在频域上将离散的傅里叶级数系数演变为连续的频谱密度函数［1-3］。

反过来，可否由非周期信号的连续频谱密度函数推导出周期信号的离散傅里叶级数呢?文献［4］利用正交积分变换的概念，首先推导出连续时间非周期信号的傅里叶变换公式，然后基于傅里叶变换的时延性质推导了理想冲激串的频谱，将连续时间周期信号看作非周期信号与理想冲激串的时域卷积，从而利用卷积性质得到周期信号的离散谱。

本文将直接从连续时间非周期信号的傅里叶变换出发，尝试从两种不同的思路得到周期信号的傅里叶级数表达，进一步阐明频谱密度函数和傅里叶级数系数之间的关系，这种思路有助于学生对傅里叶分析这一理论体系的深入理解。

下面两种分析方法中均以方波信号为例，以方便作图，其结论适用于一般的信号。假设x(t)表示位于区间［-T1，T1］之间的非周期方波信号，幅值为1，如图1(a)所示，则其傅里叶变换为

其中Sa()为抽样函数，频谱X(jω)如图1(b)所示。将x(t)以周期T0延拓成周期信号xT(t)，如图1(c)所示，需要讨论的是如何得出xT(t)所对应的傅里叶级数。

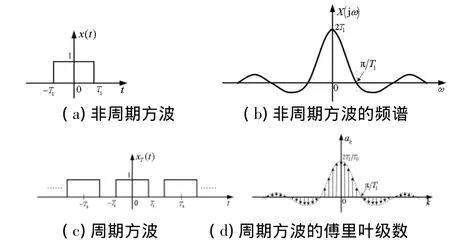
图1 非周期信号和周期信号

1 时域延拓方法

将xT(t)看作是信号x(t)在时域上以T0为周期的延拓，则

其频谱如图2(b)所示。

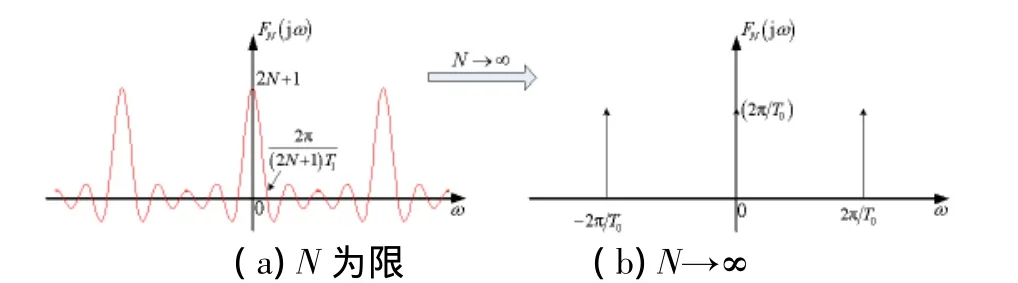
图2 N为有限值和N→∞时，FN(jω)对应的频谱

结合式(4)可得xT(t)的傅里叶变换为

可见，时域周期信号的傅里叶变换是在频率上等间隔的一组冲激函数的线性组合，其中每个冲激函数的强度正比于对应的非周期信号傅里叶变换在相应谐波频率上的离散抽样值。

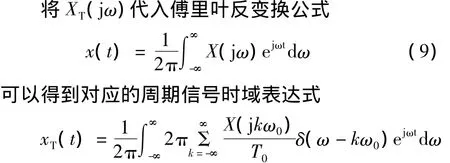
正好是时域周期信号傅里叶级数系数求解公式。

2 时域卷积方法

可见单位周期冲激串的傅里叶变换仍然是周期冲激序列，只是冲激的强度均为2π/T0。

将式(16)代入到式(14)，有

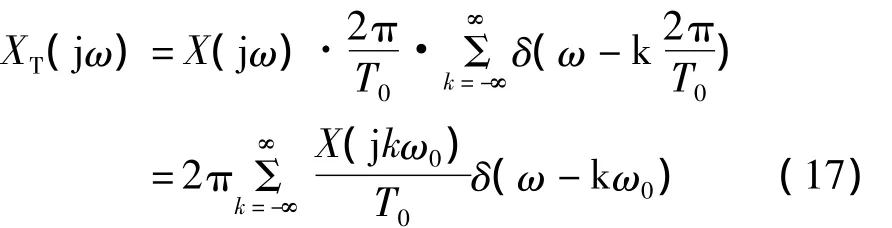
式(17)与式(8)的结果相同，因此同样可以得

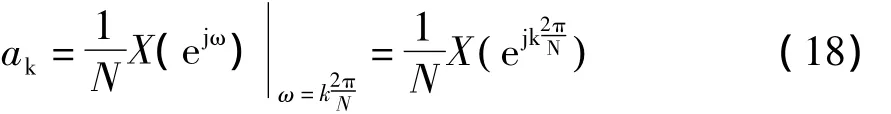
其中N为周期信号的周期。只是此时X(ejω)和ak两者均具有周期性，周期分别为2π和N。到结论:时域周期信号的傅里叶变换是在频率上等间隔的一组冲激函数的线性组合，其傅里叶级数系数正比于非周期信号傅里叶变换在相应谐波频率上的离散抽样值X(jkω0)。

至此，我们就从两条途径证明了周期信号的傅里叶级数系数和对应的非周期信号傅里叶变换之间的关系。第一条途径虽然推导过程略显繁琐，但利用了傅里叶变换的时移性质和几何级数的求值公式，有助于巩固一些重要的基本概念，强化常用的数学推演练习，可以作为学生的课外作业加以要求。

要说明的是，对于离散时间信号而言，非周期信号的傅里叶变换X(ejω)和相应周期信号的傅里叶级数系数ak之间有类似的关系，即

3 结语

在傅里叶分析的理论体系中，非周期信号的傅里叶变换和周期信号的傅里叶级数之间有着密切的联系，两者在时域上是周期延拓关系，体现在频域上即为对连续的频谱密度函数进行离散化抽样的关系，这也证实了傅里叶分析中一个域的周期性对应到另一个域中表现为离散性。本文从两个不同的思路推演了非周期信号的连续频谱密度函数到周期信号的离散傅里叶级数的变化过程，这有助于加深对两者关系的理解，更好地掌握傅里叶分析理论体系的实质。

［1］B.P.Lathi著，刘树棠译.线性系统与信号［M］.西安:西安交通大学出版社，2006.04:519-523

［2］A.V.Oppenheim著，刘树棠译.信号与系统(第二版)［M］.西安:西安交通大学出版社，1998.03:p202-205

［3］郑君里，应启珩，杨为理.信号与系统(第二版)［M］.北京:高等教育出版社，2001.04:89-113

［4］杨忠根，任蕾，陈红亮.连续信号频域分析的教学内容编排方式［J］.南京:电气电子教学学报，2010，32(5):73-75

［5］郑君里.教与写的记忆-信号与系统评注［M］.北京:高等教育出版社，2010.11:89-91