静电场导体球面与平面镜像关系研究
谢宝昌
(上海交通大学电子信息与电气工程学院,上海, 200240)
0 引言
镜像法是“电磁场”课程的重要内容之一,其本质是利用矢量场唯一性定理并通过求解区域外设置镜像电荷来等效区域边界电荷的影响,其典型实例是静电场无穷大接地导体平面和圆球面镜像的解析解,但“电磁场”相关教材主要针对镜像法的原理和求解方法,没有进一步阐述这两种镜像法的内在联系[1-4]。
本文从无穷大接地导体平面镜像出发,引入空间圆球面对称变换方法,揭示球面镜像与平面镜像的相互关系,从而获得更加简洁的求解球面镜像问题的方法,这有助于学生深入认识静电场中镜像法的本质和规律。
1 无穷大接地导体平面镜像
静电场中,点电荷关于无穷大接地导体平面镜像是电磁场中最基本的镜像问题,如图1所示,假设接地平面MN,点电荷Q及其镜像电荷Qi关于平面MN对称,建立圆球坐标系,原点位于两点电荷的连线上,求解区域在平面MN的右半空间。为了方便起见令无界空间的格林函数的圆球坐标表示为

式中,场点矢径 r(r,θ,φ),源点矢径 s(s,0,0),两者之差表示源点到场点的矢量,因此格林函数不仅具有对称性且与坐标原点位置无关,如r1=r-s和 r2=r - si[3]。

图1 无穷大接地导体平面镜像
由图1不难得到,场源点电荷Q的矢径s与其镜像点电荷Qi=-Q的矢径si之间的关系,根据对称性满足

2 圆球面对称变换
如图2所示,圆球半径a,球心为坐标原点,原来空间微元电荷量dQ及其圆球坐标s经过对称变换后分别为dQi和si,变换原则用含零矢量0的格林函数表示为式(5)表明坐标变换系数等于电荷变换系数的平方,而且逆变换具有对称性,点s与si称为变换圆球面的一对对称点,其逆变换表示为


图2 圆球面对称变换

式(9)表明变换后空间任意点(P点)r的电位φi(r)等于变换前对称点a2r/r2的电位φ(a2r/r2)与电荷量变换系数a/r的乘积,反之亦然,即经圆球面逆变换后得到原来空间电位分布也具有对称性

尽管变换前的等位面经过变换后不再保持等位面,但零电位面是例外,而且空间圆球面经过变换后仍然是圆球面或者经过原点的圆球面变换为无穷大平面。这一特点可建立起圆球面与平面镜像的联系。
3 圆球面与平面镜像转换
如图3所示,半径为a的接地导体圆球球心c,坐标原点o选择在导体圆球面上,使得球外点电荷Q位于z轴上,其点电荷到球心c距离为d,圆球坐标矢量s对称点坐标矢量为si,即满足导体球面对称变换

为了计算导体球外部电位分布,以原点为球心半径为b的圆球面进行对称变换,使得上述对称点s与si关于该圆球面仍保持对称点,则半径b为


图3 圆球面与平面镜像转换
由式(11)和(12)可知b>2a,且

式(13)表明经半径为b的圆球面对称变换后,接地导体球面变换为接地平面MN且是对称点s与si的对称平面,导体圆球内部变换到MN的右半空间,外部变换到MN的左半空间,电荷量由式(5)得到Qi=Qb/s,该电荷关于无穷大接地平面的镜像,左半空间电位分布为

式(18)代入式(17)表明,电位分布是点电荷Q关于半径为a的接地导体圆球面的格林函数表示,即球外点电荷Q与球内镜像电荷-aQ/d产生的电位合成得到球面镜像问题的解[3]。由此可见,接地导体圆球面的镜像问题可以通过圆球面对称变换将导体圆球面变换成无穷大平面,然后利用平面镜像获得求解空间的解,再经过逆变换获得实际问题的解。
特别需要强调的是式(14)和(17)与坐标原点位置无关,因此所有位置矢量可以看成是导体圆球球心位于坐标原点。式(17)中括号内的球面格林函数在导体圆球面上恒等于零,即保持零电位[3]。
如果球外电荷是分布的,式(17)是与源点坐标相关联的,那么电位分布需要采用积分形式。事实上电位分布可以分为两部分:球外分布电荷单独作用引起的电位分布φo(r),由式(7)计算,球面电荷可以等效成镜像电荷单独作用的电位分布φi(r),根据导体球面对称变换式(10)和叠加原理得到

其中,负号表示镜像电荷与源电荷符号相反。
因此接地导体圆球外分布电荷产生的空间电位

接地导体球壳内存在点电荷或分布电荷的镜像是类似的,只要将图3中s与si对称点位置交换,计算公式(11)-(20)仍然适用,不再赘述。
4 圆球导体不接地的镜像问题
如果导体圆球不接地,那么需要补充条件,球面镜像问题才能求解。
4.1 导体球面电位V0给定
1)求解圆球外部电位分布
求解导体外部电荷分布的镜像问题,可在导体球心处设置点电荷Q0,即满足球面电位等于给定值

利用叠加原理,球外电位分布等于球外电荷与接地导体球镜像电荷电位分布,再加上球心点电荷产生的球外电位,由式(20)得到
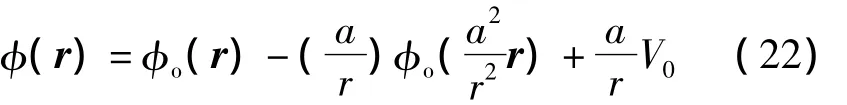
2)求解圆球壳内部电位分布
对于接地导体球壳内电荷分布产生的电位,可以根据内部电荷产生的电位φi(r)由式(7)计算,与导体球壳内表面感应电荷或等效镜像电荷分布产生的电位,再加上球壳电位V0,类似式(20)得到

4.2 导体净电荷量Q0给定
1)求解圆球外部电位分布
确定球外电荷产生的电位时,需要计算导体球接地时的感应电荷或镜像电荷总量Qit,由式(5)得到

将式(26)代入式(22)得到球外电位分布。
2)求解球壳内部电位分布
球壳内电位分布是由内部电荷、内表面感应电荷或等效镜像电荷以及外表面电荷产生的电位共同作用的结果。球壳电位由球壳外表面电荷产生,等于球壳内电荷总量Qi与球壳净电荷量Qo产生的电位之和

将式(27)代入式(23)便得到球内电位分布。
5 结语
本文利用一般圆球面对称变换建立了空间坐标、电荷量变换关系和电位分布计算关系,获得特殊条件下球面镜像与平面镜像的联系,推导了点电荷球面镜像的平面镜像法计算公式,并将公式推广而且简化了分布电荷球面镜像的计算公式,进一步讨论了导体圆球或球壳不接地情况下内、外空间电位分布的计算公式。理论研究揭示了导体平面和球面两种镜像法的内在联系和变换关系,这将有助于学生深入理解“电磁场”教材中静电场镜像法的内容。
[1]周希朗.电磁场.北京:电子工业出版社,2008年
[2]谢处方,饶克谨.电磁场与电磁波.北京:高等教育出版社,第4版,2006年
[3]王蔷,李国定,龚克.电磁场理论基础.北京:清华大学出版社,2001年
[4]陈重,崔正勤,胡冰.电磁场理论基础.北京:北京理工大学出版社,第2版,2010年

