半潜式钻井平台用钢DH36安定行为试验研究

孙 阳，章家宝（河海大学 港口海岸与近海工程学院，南京210098）

半潜式钻井平台用钢DH36安定行为试验研究

孙 阳，章家宝
（河海大学 港口海岸与近海工程学院，南京210098）

为了给半潜式钻井平台的安全性和寿命评价提供可靠试验依据，在室温下对半潜式钻井平台用钢DH36钢进行了考虑加载波形、加载速率和应力比影响的多工况单轴棘轮安定试验。结果表明：循环硬化速率随循环周次的增加快速下降，在低于某一值的循环应力作用下，应变将最终趋于棘轮饱和状态；正弦应力波比三角波更快地趋于安定，采用较低的加载速率可以加速材料趋向饱和棘轮状态；峰值应力固定不变时，棘轮应变对应力比历史无明显的记忆性；波形和加载速率对饱和棘轮应变的影响有限，饱和棘轮应变随着应力峰值的增加而增大。

半潜式钻井平台；DH36钢；棘轮安定；加载波形；加载速率；应力比

0 引 言

金属材料在非对称应力循环载荷作用下将会产生一种称之为棘轮效应的塑性变形循环累积现象[1]，并且不同材料的棘轮效应特征是明显不同的[2-3]。安定是指材料在经历一定循环次数之后，棘轮应变率低于某一特定值，即认为此时棘轮效应达到饱和，材料处于某种棘轮安定状态。在一定应力范围内的加载工况下，棘轮效应不会促使材料塑性变形累积无限发展至破坏，此时材料在经历一定的循环次数后达到棘轮安定状态[4]。棘轮行为对承受非对称应力循环加载的工程结构的安全性和寿命评价是非常重要的，目前已引起人们的广泛重视。

近年来，已有不少学者对不同材料的棘轮行为进行了室温和高温下的一些实验研究，并在实验基础上发展了一些描述棘轮行为的循环本构模型[5-10]。然而，由于棘轮行为的复杂性和不同材料循环特性的差异，以及这些研究中侧重于对实际工程更有意义的材料安定行为的研究较少，要全面揭示材料的安定行为还需进行大量深入的试验研究。

本文在室温下对半潜式海洋钻井平台用钢DH36进行了考虑加载波形、加载速率、应力比影响的多工况单轴棘轮安定试验，揭示了该材料应力循环下棘轮安定行为特性，结果可为安定性数值分析方法在承受交变循环荷载作用的半潜式海洋钻井平台结构强度评估中的实施提供可靠的试验依据。

1 试验条件

本文试验所采用的材料为DH36钢，该种钢为建造和修理半潜式钻井平台的专用碳素钢。为使材料结构组织均匀、力学性能稳定，将母材经800℃保温60分钟，进行水冷固溶处理后，加工成实心圆棒试样，试样尺寸如图1所示。实心圆棒试样中心标距段的直径为6 mm，等直段长度为30 mm，两边夹头直径为18 mm、长度为50 mm[11]。

试验用设备为MTS809（250kN）拉—扭电液伺服控制试验机，控制系统为TeststarⅡ。试验中的循环加载过程采用应力控制，按时间同步采集连续的轴向载荷和它们的峰谷值数据。

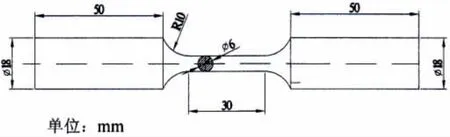
图1 DH36钢试样尺寸Fig.1 Dimension of the specimen

2 试验内容、结果及讨论

2.1 棘轮安定的界定

由于应力控制循环中，滞后环一般都不是完全封闭的，因此，将棘轮应变定义为[12]：

式中：εmax为一个加载循环中最大轴向应变，εmin为一个加载循环中最小轴向应变。如果材料的棘轮行为达到安定状态，则称此时材料的棘轮应变为饱和棘轮应变，记为

单轴条件下的棘轮应变率ε˙r反应了棘轮应变随着循环次数的变化情况，定义为：

式中：N是循环次数，dεr表示每一次循环中棘轮应变εr的增量。本文取文献[10]中ε˙r＜1×10-7mm/mm/ cycle为安定界定标准。经过取试件进行百万周次的循环加载验证，以此标准作为安定界定标准是十分可靠的。

图2给出了循环加载时钢材两种不同的εr-T响应曲线，当最大应力低于某一值时，随着循环次数的增加，应变最后趋于收敛，达到棘轮安定状态；当最大应力增加到超出某一值时，棘轮安定状态被改变，棘轮应变率不等于零，应变随着循环次数的增加不断累积，直至最终破坏。

2.2 加载波形对DH36钢安定行为的影响

在平均应力、应力幅、周期相同的情况下，对正弦加载与三角形加载情况进行比较，考察不同加载波形对试件棘轮安定行为的影响。取三种工况包括正弦波、三角波、正弦波和三角波交替分别对试件进行循环加载，表1给出了加载工况，表中σm表示加载平均应力，σa表示加载应力幅。

图2 循环加载时两种不同的εr-T关系曲线Fig.2 Two types of εr-T curves under cyclic loading

表1 不同加载波形工况Tab.1 Different conditions of loading wave forms

图3给出了表1中工况1、工况2分别循环加载10 000T时的εr-T关系曲线，图中σmin为加载过程中最小应力值，σmax为峰值应力值。由图可以看出，在两种波形作用下，材料均体现出了明显的循环硬化特性，并具有相同的演化规律。最终应变均达到了稳定状态，即应变不再随着循环周次的增加而变化。图3所反映出的不同变化规律是，正弦应力波形作用下的饱和棘轮应变均都略高过同平均应力、同应力幅、同周期的三角波，即正弦应力波比三角波更快地趋于安定。这种现象应该主要是因为正弦波形的应力峰谷值处加载率极小，相当于在循环峰谷值的高应力区有荷载保持，由此增大的应变则包含有类似于蠕变的变形。

图3 不同加载波形的εr-T关系曲线Fig.3 Curves of εr-T under different loading waves

图4三角波的荷载—应变关系Fig.4 Relationships between load and strain under triangular loading waves

图4 给出了三角波加载时四种不同周期10T、200T、3 000T、4 000T下的荷载与应变之间的关系，由图可以看出，每一级加载下的循环硬化速率随循环周次的增加快速下降。10T时，加、卸载曲线明显不重合，应变随着循环加载过程的进行，不断增长，但卸载过程没有发生反向屈服。到200T时，加、卸载曲线已比10T时明显的接近，表明应变速率在不断减小。3 000T时，加、卸载曲线基本上已经重合，呈一条直线状，即此过程中，应变不随荷载施加方式发生变化，荷载—应变是弹性关系。4 000T和3 000T的加、卸载曲线也是重合的，说明荷载—应变关系不但在加、卸载过程中是弹性的，而且不随新的加载循环次数的变化而变化，应变达到了稳定状态。出现这种现象的原因是由于经过较大平均应力的应力循环后，材料内部的位错密度升高，位错组态也逐渐变成较为稳定的位错胞状结构，材料产生了较大的循环硬化，变形阻力增加，不易产生新的塑性变形，从而使后续应力循环下的棘轮应变率明显下降。正弦波以及后续的加载工况中也都存在类似的情况，不再重复赘述。

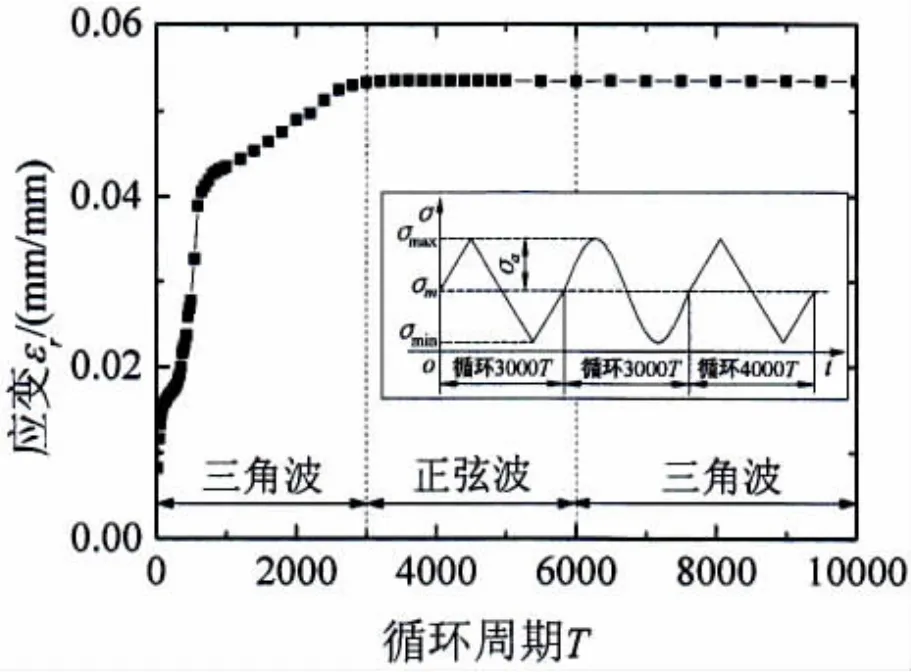
图5交替加载波形下的εr-T关系曲线Fig.5 Curves of εr-T under alternating loading waves

图5 给出了表1中工况3两种波形交替加载循环10 000T得到的εr-T试验结果，由图可以看出，应变εr最终也达到了稳定状态，且饱和棘轮应变与图3中三角波和正弦波的饱和棘轮应变相差不大。应变达到稳定前，波形历史对棘轮应变的变化过程有一些影响；应变达到稳定后，波形历史对饱和棘轮应变影响不大。

2.3 加载速率对DH36钢安定行为的影响

三角波加载，采用四种工况考察加载速率对棘轮安定的影响，工况如表2所示。

表2 不同加载速率工况Tab.2 Different conditions of loading rates

图6 不同加载速率下的εr-T关系曲线Fig.6 Curves of εr-T under different loading rate

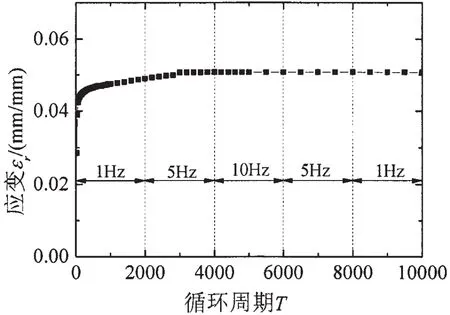
图7 加载速率历史下的εr-T关系曲线Fig.7 Curves of εr-T under history of loading rate

图6给出了表2中工况1、工况2、工况3各循环加载10 000T得到的εr-T试验结果，由图可以看出，在三种加载速率下，材料具有相同的应变演化规律。应变随循环周次的增加而增大，应变速率随循环周次的增加而逐渐下降，且三种加载速率下的应变εr最终都达到了稳定状态。三种工况加载速率的最终饱和棘轮应变差别不大，随着应力加载速率的降低，产生的饱和棘轮应变略有增加。在选定的试验条件下，加载速率对最终饱和棘轮应变的影响有限。

图7给出了表2中工况4三种加载速率1 Hz、5 Hz、10 Hz交替加载得到的εr-T试验结果，由图可以看出，最终应变也达到了稳定状态。和图6相比，加载速率的交替变化对εr-T曲线的变化过程无明显影响，且对最终饱和棘轮应变的影响也非常有限。

2.4 应力比对DH36钢安定行为的影响

将定义应力比为：

应力比可以综合反映加载应力幅、平均应力以及峰值应力对棘轮应变的影响，三角波循环加载，采用三种工况考察应力比对DH36钢安定行为的影响，工况如表3所示。

表3 不同应力比工况Tab.3 Different conditions of stress ratio

图8 峰值应力固不变时不同应力比下的 εr-T关系曲线Fig.8 Curves of εr-T under different stress ratio with the same peak stress

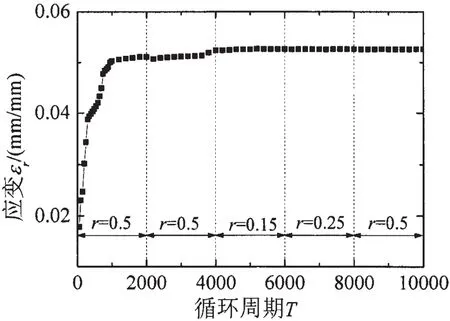
图9峰值应力固不变时应力比历史下的 εr-T关系曲线Fig.9 Curves of εr-T under history of stress ratio with the same peak stress

图8 给出了表3中工况1在峰值应力固定不变的情况下，三种不同应力比r=0.15、r=0.25、r=0.5时的εr-T关系曲线试验结果。由图可以看出，εr随着T的增加不断衰减，最终都达到了稳定值。峰值应力不变，最小应力值变化意味着平均应力和应力幅的变化。同时，图8显示应力比对初始阶段的棘轮应变演化规律有一定影响。当r较大，即平均应力比较大而应力幅比较小时，棘轮应变经过衰减阶段后会很快产生达到安定，也就是说三种应力比作用下棘轮应变达到稳定的速度为：r=0.5>r=0.25>r=0.15。

图9给出了表3中工况2在峰值应力固定不变的情况下，三种不同应力比r=0.15、r=0.25、r=0.5交替变化得到的εr-T关系试验结果。同样，棘轮应变也是随着T的增加不断衰减，最后达到了稳定状态。

图10给出了表3中工况3在最小值应力固定不变的情况下，三种不同应力比r=0.211、r=0.2、r= 0.186交替变化得到的εr-T关系曲线试验结果。由图可以看出，试件对加载历史中的最大峰值应力值循环特性具有明显的记忆效应，先前较大峰值应力循环会抑制后续较小峰值应力循环的棘轮行为，棘轮行为也具有明显的峰值应力历史依赖性；低峰值应力棘轮历史对后继高峰值应力水平下的饱和棘轮应变状态影响微弱，饱和棘轮应变和峰值真应力之间存在着不受先前低峰值应力棘轮历史影响的关系。

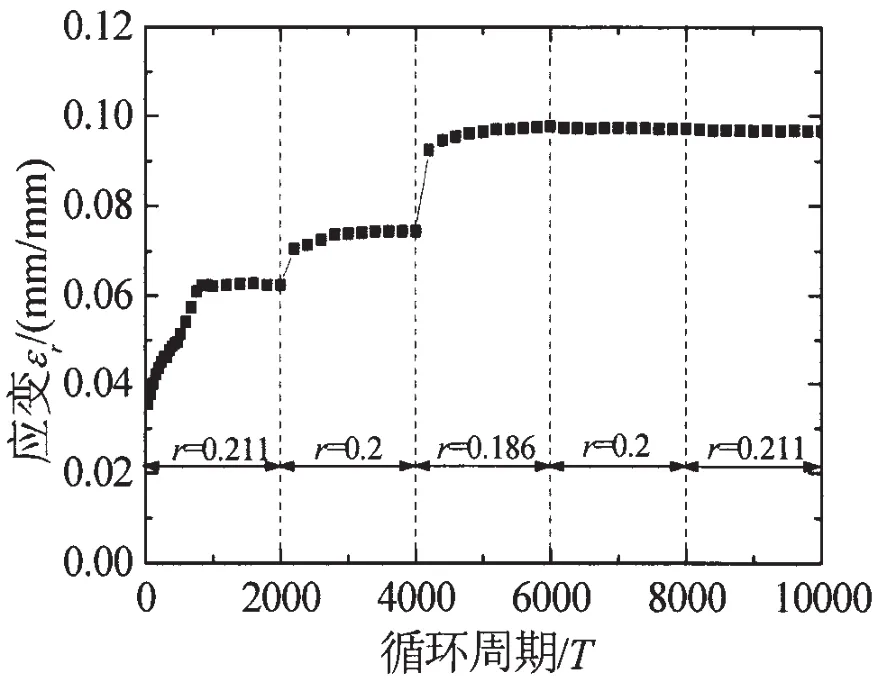
图10 最小应力固不变时不同应力比历史下的εr-T关系曲线Fig.10 Curves of εr-T under history of stress ratio with the same minimum stress

3 结 论

（1）不同工况下，DH36钢的试验结果显示均体现出了明显的循环硬化特性，并具有类似的演化规律。循环硬化速率随循环周次的增加快速下降，在低于某一值的应力作用下，应变将最终趋于棘轮饱和状态。

（2）在平均应力、应力幅和周期相同的情况下，波形对棘轮应变的变化过程有一些影响，尤其是对加载初期，正弦波形作用下的饱和棘轮应变略高过三角波，正弦应力波比三角波更快地趋于安定；波形对饱和棘轮应变的影响较小。

（3）在等幅值、等平均应力条件下，加载速率对初始阶段的棘轮应变量有明显的影响，加载速率越低，相同循环次数下的棘轮应变越大，采取较低的加载速率可以加速材料趋向饱和棘轮状态。不同加载速率对饱和棘轮应变的影响有限。

（4）峰值应力固定不变的情况下，较大的应力比能使棘轮应变经过衰减阶段后会更快达到安定，应力比未对饱和棘轮应变产生明显的影响，且棘轮应变对应力比历史无明显的记忆性。最小应力固定不变的情况下，应力峰值对饱和棘轮应变有明显的影响，饱和棘轮应变随着应力峰值的增加而增大。

[1]Xia Zihui,Ellyin F.A constitutive with capability to simulate complex multiaxial ratcheting of materials[J].International Journal of Plasticity,1997,13:127-142.

[2]杨显杰,罗 艳,高 庆等.循环软化45碳钢和循环硬化304不锈钢的棘轮行为实验研究[J].固体力学学报,2005, 26(2):125-131. Yang Xianjie,Luo Yan,Gao Qing,et al.A study on the ratcheting behavior for cyclic softening 45 carbon steel and cyclic hardening 304 stainless steel materials[J].Acta Mechanica Solida Sinica,2005,26(2):125-131.

[3]Yang Xianjie.A viscoplastic model for 316L stainless steel under uniaxial cyclic straining and stressing at room temperature[J].Mechanics of Materials,2004,36(11):1073-1086.

[4]Liu Yujie,Kang Guozheng,Gao Qing.Stress-based fatigue failure models for uniaxial ratchetting-fatigue interaction[J]. International Journal of Fatigue,2008,30:1065-1073.

[5]Kang Guozheng,Gao Qing,Yang Xianjie.Experimental study on the cyclic deformation and plastic flow of U71Mn rail steel[J].International Journal of Mechanical Sciences,2002,44:1647-1663.

[6]Kang Guozheng,Gao Qing.Uniaxial and non-proportionally multiaxial ratcheting of U71Mn rail steel:Experiments and simulations[J].Mechanics of Materials,2002,34:809-820.

[7]Heitzer M,Staat M,Reiners H,et al.Shakedown and ratcheting under tension-torsion loadings:analysis and experiments [J].Nuclear Engineering and Design,2003,225:11-26.

[8]Cai Lixun,Niu qinyong,Qiu shaoyu,et al.Ratcheting behavior of T225NG titanium alloy under uniaxial cyclic stressing: Experiments and modeling[J].Chinese Journal of Aeronautics,2005,18(1):31-39.

[9]Barker M G,Bergson P M,French C E.Shakedown tests of one-third-scale composite bridge[J].Journal of Bridge Engineering,2006,2:2-9.

[10]史 智,高 庆,康国政等.1Cr18Ni9不锈钢高温单轴时相关棘轮行为研究[J].工程力学,2007,24(9):159-165. Shi Zhi,Gao Qing,Kang Guozheng,et al.Uniaxial time-dependent ratcheting behaviors of 1Cr18Ni9 stainless steel at elevated temperature[J].Engineering Mechanics,2007,24(9):159-165.

[11]孙 阳.结构安定性数值分析方法及其工程应用研究[D].上海:上海交通大学博士学位论文,2011,24. Sun Yang.Numerical methods of shakedown analysis with its application[D].Shanghai:Shanghai Jiao Tong University, 2011,24.

[12]刘宇杰.金属材料的棘轮行为研究[D].成都:西南交通大学,2004:2-3. Liu Yujie.Ratchetting of metal materials[D].Chengdu:Southwest Jiaotong University,2004:2-3.

Experimental study on shakedown behavior of DH36 steel used for semisubmersible

SUN Yang,ZHANG Jia-bao
(College of Harbour,Coastal and Offshore Engineering,Hohai University,Nanjing 210098,China)

In order to provide experimental basis for evaluation of safety and life of semisubmersible,the shakedown behavior of DH36 steel used for semisubmersible was experimentally investigated under uniaxial cyclic loading at room temperature.The effects of loading rates,loading wave forms and stress ratio on the ratcheting of DH36 steel were analyzed.The experimental results show that the rate of cyclic hardening rapidly decreases with the increase of loading cycles,and the stress amplitude will becomes gradually saturated when the cyclic strain is below a certain value.A quick shakedown of ratchetting was observed from sine loading waves instead of triangular loading waves and lower loading rates could accelerate cyclic saturation.With the same peak stress,ratcheting strain presents no memorization on previous stress ratio in loading history.Loading wave forms and loading rates hardly influence the saturated ratcheting strain of the material and saturated ratcheting strain increases with the peak stress.

semisubmersible;DH36 steel;shakedown behavior;loading wave forms; loading rates;stress ratio

TU502

A

10.3969/j.issn.1007-7294.2015.07.008

1007-7294（2015）07-0827-07

2015-03-27

国家自然科学基金资助（51309151）；海洋工程国家重点实验室开放课题研究基金资助（1107）；中央高校基本科研业务费专项资金资助（2014B17414）

孙 阳（1979-），男，博士，副研究员，E-mail：yangsun_mail@126.com；

章家宝（1980-），男，硕士，工程师。