细长轴双刀车削加工让刀量误差优化的研究与应用
张正义,刘芳
(1. 西华大学机械工程与自动化学院,四川成都610039;2. 中原工学院机电学院,河南郑州450007)
0 前言
在车削加工中,细长轴(长度与直径的比值大于20 的轴)由于长径比大,在切削过程中极易产生振动、弯曲变形等不利因素,传统的加工方法很难满足对零件加工精度的要求,所以寻找提高细长轴加工精度的突破口就尤为重要。自误差补偿技术自提出以来广泛用于数控机床加工精度的提高,包括机床热变形误差补偿、运动误差补偿以及刀具切削力变形误差补偿[1-2]。文献[3]分析了车削细长轴时非线性振动对其加工精度的影响,对实际生产中细长轴的加工有指导作用。文献[4]通过运用神经网络建立跟刀架车削细长轴的尺寸误差预测模型,研究了不同切削用量对加工精度的影响。文献[5]通过用进刀量补偿法减少细长轴的加工误差,提高了细长轴的加工精度。文献[6]通过对细长轴车削用量优化与加工变形误差补偿技术的研究,有效解决了细长轴类零件的加工变形问题。
以上方法对细长轴的车削加工精度的提高都有一定的帮助,但是在加工精度要求很高的情况下还存在缺陷。本文作者通过建立细长轴双刀车削模型,推导出刀具加工点理论让刀量公式,然后进行仿真优化,并将优化的公式作为补偿函数进行细长轴的车削实验,与没有补偿函数的细长轴车削加工对比,结果表明,采用优化后的刀具加工点让刀量公式作为补偿函数能显著提高细长轴的加工精度。
1 刀具加工点退让量理论分析
细长轴的车削加工通常采用一夹一顶的装夹方式,将三角卡盘一段简化为固定端并限制全部自由度,弹性顶尖一端简化为铰支端,建立xoz 平面细长轴双刀车削径向力受力车削模型,如图1 所示。
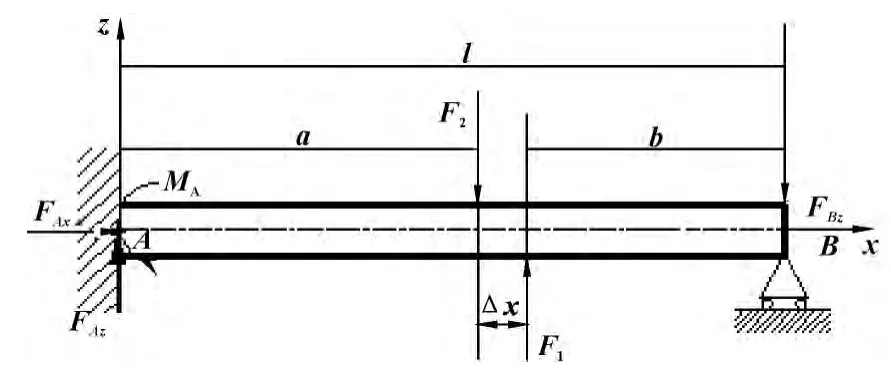
图1 细长轴双刀车削受力模型
图1 为细长轴双刀车削在xoz 平面的受力分析模型,F1、F2为主切削力,假设两把刀具的背吃刀量相等,那么F1=F2。两把刀具之间的横向距离Δx 相对于l 来说很小,所以把主切削力F1、F2等效为力偶MF,力偶MF位于主切削力F1、F2中点位置。

其中±与w合同号,MF=ΔxF1
由此可知,式(2)中MA、FAz为未知量,要求解必须补充一个变形方程。利用奇异函数法写出细长轴的挠曲线方程,奇异函数定义:若x <a,则量<x-a >=0;若x >a,则<x-a >= (x-a)。
根据边界条件:x =0,w =0,w' =0 以及x =l,w=0 求解上式,得到细长轴的挠曲线方程。
假如只研究因刀具径向力产生的弯曲变形,分离出刀具的进给力,则FAxw合因子为0,对式(3)进行一次、二次积分,并由边界条件得:
令x=a+Δx,则b=l-x,MF=F径Δx
由此可得细长轴车削时刀具在加工点的理论让刀量方程:
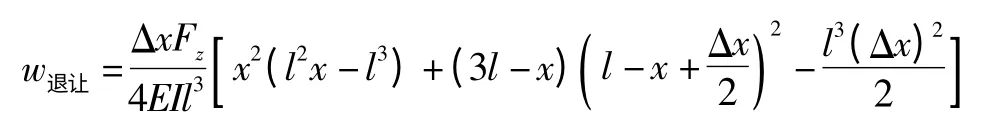
2 刀具加工点退让量仿真分析及优化
运用有限元法对细长轴双刀车削进行静力学分析,在仿真分析之前,考虑到细长轴实际切削过程中各因素的相互影响,为便于研究,在仿真过程中做如下假设:(1)刀具不产生任何磨损或变形;(2)切削过程中径向力恒定不变; (3)仿真过程中切削力为背吃刀量为1 mm 时的值。
图2 为细长轴有限元的网格模型,细长轴双刀车削模型是以梁理论为基础建立的简支梁模型,文中仿真分析考虑实际情况选用Beam188 单元,该元素是基于Timoshenko 梁理论建立的。仿真结果的准确性和网格划分的精细程度相关,网格划分得越精细,仿真结果越准确,考虑到实验数据的计算和处理,仿真模拟将细长轴有限元模型在x 轴方向上离散划分为100 份,对应的节点数为100 个。图3 为细长轴双刀车削有限元仿真分析模型。
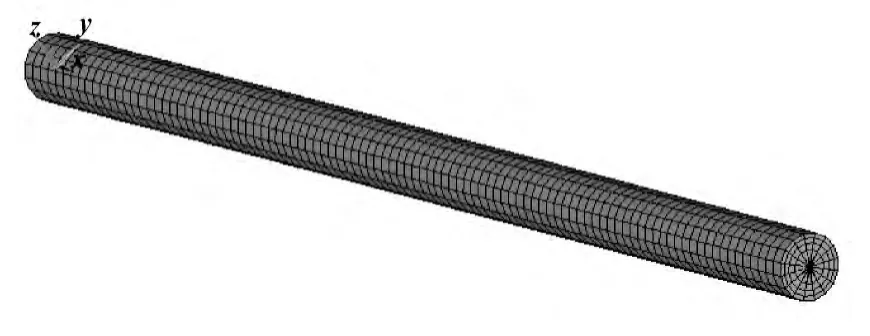
图2 细长轴有限元网格模型
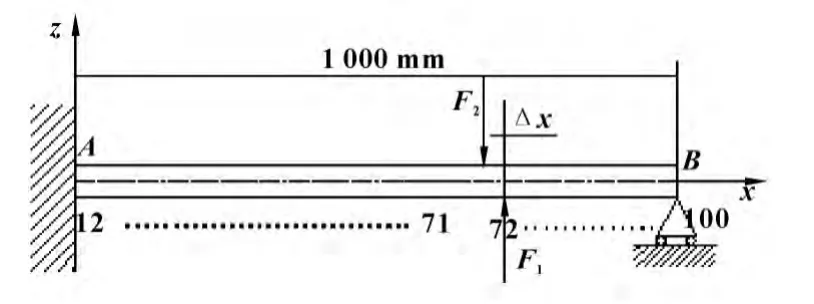
图3 双刀车削有限元仿真模型

表1 仿真模型参数
刀具径向力为实验所得,根据仿真要求,定义仿真分析类型为静力分析,依据上文简化的模型,设置在1 号节点处施加全约束,在2 号节点处施加y、z 方向的位移约束。载荷设置为分布载荷,每一步为10 个节点,图4 为细长轴双刀车削弯曲变形图。

图4 双刀车削加工零件变形图
在后处理中,利用查看节点位移命令,显示出每一步刀具所在点的z 方向上位移作为刀具加工点的让刀量,经过整理数据如图5 所示。
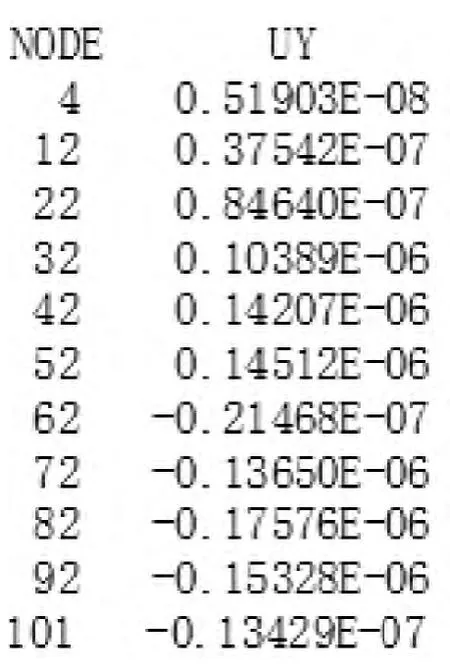
图5 节点数据
由于细长轴在加工过程中产生了弯曲变形,导致了刀具理论加工点的位置发生了变化,造成了工件加工尺寸误差,如果预测出刀具加工点的让刀量,便可以知道工件的尺寸误差,提前在误差点进行防范。让刀量的预测对细长轴的加工有着重要的指导作用,而且也为数控编程实施刀具补偿提供了运动轨迹。由刀具分力与背吃刀量近似成正比的关系[7],引入修正系数k,得到细长轴在刀具加工点的让刀量预测公式为:
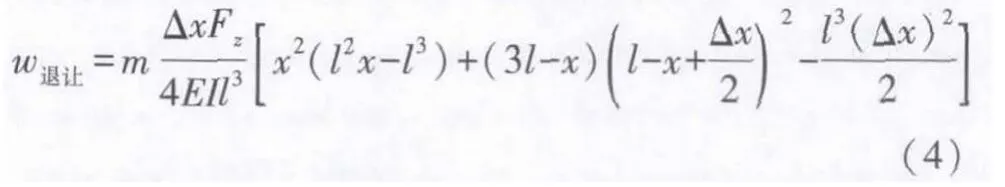
其中k 为引入的切削径向力修正系数。
将l=1 000 mm,d =50 mm,F =78 N,E =2.1×1011Pa,Δx=10 mm,I=代入式(4),得出细长轴双刀车削刀具加工点实际让刀量预测公式:

利用Matlab 软件对式(5)进行求解,分别绘制出了修正系数k 取1,1.1,1.2 时的曲线,把细长轴轴向坐标(节点按所在位置进行转化)设置为横坐标(x 轴),把刀具加工点的退让量作为纵坐标(y轴),坐标原点为卡盘固定端,绘制曲线如图6 所示。
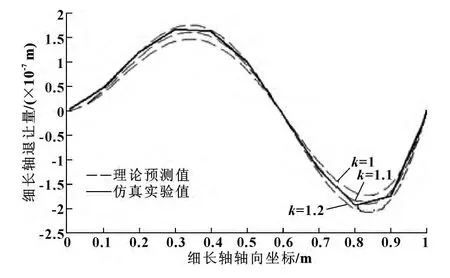
图6 节点退让量曲线
由图6 可以看出,当修正值k =1.1 时,预测值和仿真值相差最小,绘制的曲线最相近,所以建议k的初修正值为1.1。
3 实验验证
为验证在实际生产过程中让刀量预测公式在数控补偿系统中的加工效果,文中进行了实验切削,实验机床选用NZ-S1500/1000 双刀塔车床。实验工件材料选用45 钢,长L=1 000 mm,直径d =50 mm,已经完成粗加工;实验刀具选用硬质合金可转位车刀,车刀几何角度:主偏角Kr=90°,前角γ0=15°,刃倾角λs=5°,后角α0=60°;实验切削参数:切削速度150 m/min,进给速度0.6 mm/min,背吃刀量ap1=1 mm,ap2=1 mm。
实验分为两组,一组为不采用让刀量预测公式直接车削加工,另一组采用让刀量预测公式进行车削加工。实验结束后用千分尺分别测量十组不同位置的直径,结果见表2。

表2 实验数据
利用Excel 软件,以细长轴直径为纵坐标,以轴的轴向坐标为横坐标,设置细长轴卡盘固定端为坐标原点,绘制出加工细长轴直径-轴横向位置坐标的曲线图,如图7 所示。
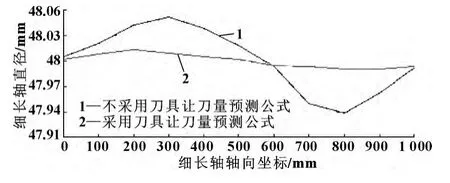
图7 细长轴直径-轴横向位置坐标的曲线图
由图7 可以看出:虽然由实验数据得出的曲线和仿真曲线存有一定差异,但曲线的总体趋势基本一致;采用刀具让刀量预测公式作为补偿函数车削细长轴的直径误差明显低于不采用刀具让刀量预测公式作为补偿函数车削细长轴的直径误差,并且最大误差值减小0. 053 mm。由此证明了采用刀具让刀量预测公式作为补偿函数可明显提高细长轴加工精度,并为数控车削细长轴提供了补偿方程。
4 结束语
通过对细长轴双刀车削的静力学仿真分析,得出刀具在加工点的退让量数据,利用Matlab 对预测的理论分析曲线进行优化,并和仿真曲线进行对比,得出径向力修正系数k 的取值为1.1。通过数控实验验证,采用刀具让刀量预测公式作为补偿函数车削细长轴可大幅度提高细长轴的加工精度,并且该研究在其他细长轴类零件的车削加工过程中具有指导意义。
[1]李玉玲,李志峰,魏伟锋.车削加工细长轴的理论误差分析[J].煤矿机械,2008,29(10):108-109.
[2]刘龙田.用进刀量补偿法减小细长轴车削加工误差[J].电子设计与工程,2012,20(21):100-102.
[3]王小翠,李蔚,侯志敏.细长轴车削用量优化与加工变形误差补偿技术的研究[J].制造技术与机床,2007(10):85-88.
[4]韩荣第,崔伯第.基于神经网络的细长轴车削加工尺寸误差预测研究[J].工具技术,2002,42(5):9-11.
[5]许文韬,岳鹏程,宋有为.普通车床的对称式双刀车削[J].机械工程师,2007(9):135-136.
[6]江平.细长轴车削加工过程的有限元仿真分析[D].成都:西华大学,2012.
[7]BALLO I.Non-linear Effects of Vibration of a Continuous Transverse Cracked Slender Shaft[J].Journal of Sound and Vibration,1998,217(2):321-333.

