基于BP神经网络的麦蚜最大虫株率预测

靳然，李生才

（山西农业大学 农学院，山西 太谷030801）

多年来，众多昆虫学家和植保工作者致力于病虫害测报方法的研究，发展了经验预测法、实验预测法和统计预测法等传统预测预报方法［1］。但由于害虫的发生具有多样性、突发性、随机性等特点，易受环境因子及害虫自身生长发育、天敌发生情况等影响，其所在的生态系统是一个非常复杂的非线性结构，传统的预测预报方法很难达到理想的效果。近年来，专家、学者将现代非线性理论运用到害虫测报领域，将传统的动力学理论、数理统计与现代计算技术相结合，发展了人工神经网络、相空间重构预测法、小波分析、支持向量机等病虫害测报新方法［2～4］。

目前，人工神经网络在预测方面已有较多的应用，如地质灾害的发生、房地产走向、借贷风险分析等，在害虫预测预报方面也取得了一定的成果。陈恩会等［5］做了关于BP神经网络在病虫预测预报中的应用介绍；王国昌等［6］研究了近年来人工神经网络在农林害虫的识别和诊断，并且建立了发生期和发生量的预测预报模型；欧钊荣等［7］根据广西甘蔗棉蚜虫发生情况基本资料和气象指标建立了BP神经网络预报模型，拟合程度和预报精度都比较高；唐建军等［8］建立了水稻虫害发生量预测预报的BP神经网络预测系统，确定了自然因素与发生量之间的关系。

麦蚜以成虫和若虫刺吸小麦茎、叶和嫩穗的汁液。小麦苗期受害，轻者叶色发黄、生长停滞、分蘗减少，重者麦株枯萎死亡。穗期受害，麦粒不饱满，严重时麦穗干枯不结实，甚至全株死亡。此外，麦蚜还可以传播多种麦类毒素病。据资料统计，上世纪50～60年代，麦蚜的发生较为平稳，危害较小，年发生面积一般在190～460万hm2之间。70～80年代，麦蚜发生量逐渐增大，由间歇性严重发生逐渐转为经常性发生主要害虫，危害面积呈不断上升趋势，成为我国小麦作物重大害虫之一。进入90年代，麦蚜发生面积急剧上升，由1972年的342万hm2迅速上升到1999年的1838万hm2，导致小麦产量年损失达到50万t以上，占小麦病虫害造成损失总量的1／3。尤其是90年代中后期，从发生面积、防治后的实际损失方面来看，小麦蚜虫已上升为继水稻飞虱、水稻纹枯病之后的我国农作物重大病虫害中的第3位［9］。

对麦蚜发生的预测研究自上世纪80年代末开始，迄今近30年，已运用马尔柯夫链、列联表法、逐步回归法、模糊数学等方法进行预测，并取得一定的效果，但运用BP神经网络对麦蚜发生进行预测尚属空白。与其它方法相比，BP神经网络预测模型模拟人脑结构设计，预测结果更科学和精确。本文以1980—2006年气象因子和历年最大虫株率为基础，建立基于BP神经网络的麦蚜虫株率预测模型，并将逐步回归法预测结果作为对比，试图探索建立更加准确和稳定的病虫害测报模型。

1 材料与方法

1.1 麦蚜数据

麦蚜原始数据来自山西省植保植检总站，数据采集点在山西运城市芮城县古魏镇，为山西小麦的主产 区，北 纬 34°36′～48°30′，东 经 110°36′～42°30"，年平均气温12.77℃，无霜期250d左右，年降水量513mm。全镇耕地面积约4 700hm2，土地平坦，土壤肥沃，小麦是最主要的农作物。虫害统计资料为1980—2011年间2月底到6月初，采用系统调查法每5d采集一次数据。

1.2 气象数据

气象数据来自山西省气象局。以1980—2006年，每年2月1日到5月10日的气象数据为基础，统计得到月平均温度、月平均最高温度、月平均最低温度、月平均湿度、月平均降水量、月平均日照时数、月平均风速等作为单一气象指标；计算复合气象指标，包括每月的温雨系数（降雨量／平均气温）、晴雨系数（降雨量／日照时数）、温湿系数（平均湿度／平均气温）［10］；将单一气象指标与复合气象指标共同建表（表1）。

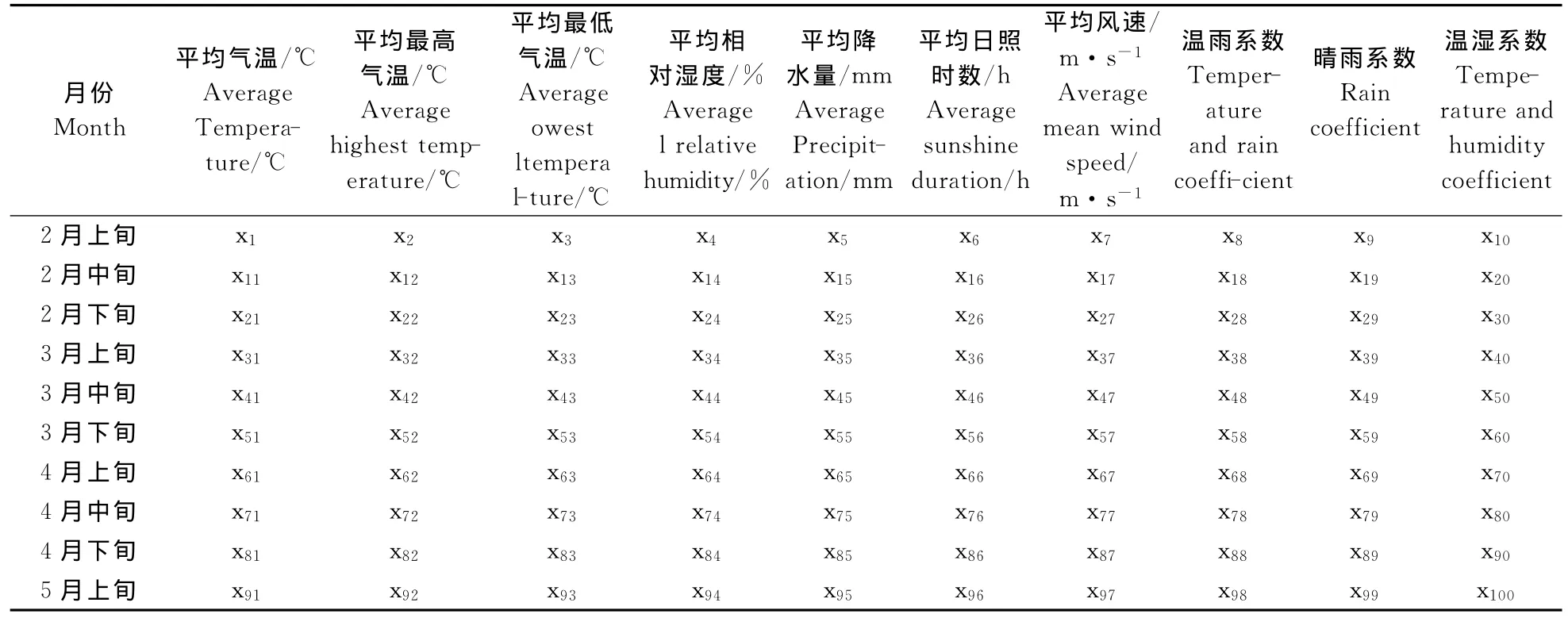
表1 气象因子对照表Table1 The contrast table of meteorological factor

1.3 归一化法处理数据

由于各气象因子量纲和数量级单位均不同，因此在建模之前，要将所有变量进行变换处理，使所有变量处于一个标准的范围内。常用的数据处理方法有归一化法、极差正规化法、标准化法、对数变换法等，本实验采用较常用的归一化法对所有变量进行预处理。

神经网络对［0，l］间的数据最敏感［11，12］，在建模之前，将成分因子归一化处理到［0，l］范围内。归一化公式为：

式中，xi表示数据原始值，x表示归一化后的数据，xmax、xmin分别表示每一类成分因子的最大值和最小值。

1.4 BP神经网络介绍及建模程序

神经 网 络 （artificial neural network，缩 写ANN）模拟人脑结构设计，是人脑的一种物理抽象、简化和模拟，具有很强的非线性信息处理能力，人工神经元通过不同联结方式组成网络结构［13］。神经网络具有非线性、非局限性、非常定性、非凸性等四个基本特征，采用并行分布式系统，克服了传统的基于逻辑符号的人工智能在处理直觉、非结构化信息方面的缺陷，具有良好的自适应、自组织和自学习能力［14］。神经网络的类型很多，网络结构和学习算法不同，可分为单层前向网络、多层前向网络、反馈网络、随机神经网络等类型，常用的有BP神经网络、小波神经网络、模糊神经网络、径向基神经网络等。

本实验采用MATLAB软件编写神经网络程序，建立BP神经网络模型，将1980—2006年作为训练集进行建模，2007—2011年作为测试集进行预测，具体预测流程如图1所示。

将1980—2006年麦蚜最大虫株率作为训练集，2007—2011年麦蚜最大虫株率作为测试集。建模程序分为数据归一化、网络训练、网络预测、误差分析、结果作图等过程。在本实验中设计的神经网络为3层结构，由一个输入层、一个隐含层和一个输出层组成，进行网络训练时选择LM算法。神经网络的参数很多，有输入层节点数、隐含层节点数、输出层节点数、传递函数、训练函数、学习率等［15］。在网络结构、权重及阈值相同的情况下，隐含层节点数及传递函数的选择，直接影响着网络的学习能力和泛化能力［16］，根据经验，本实验中设定输入层节点数为100，隐含层节点数为10，输出层节点数为1，训练迭代过程30，动量因子为0.9，训练步数30，学习率0.1，期望目标误差最小值10－5。

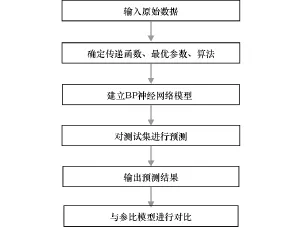
图1 BP神经网络预测流程Fig.1 The prediction flow of BPNN

BP神经网络选用Sigmoid函数作为隐含层的传递函数，其定义如下：

S（x）＝ 1 1＋e－t

Sigmoid主要有三种类型，分别为logsig函数、tansig函数及purelin函数。本实验设置的隐含层传递函数为tansig，输出层传递函数为purelin。

1.5 参比模型

为评价BP神经网络预测模型的优劣，选择目前在病虫害预测预报领域较为常用的逐步回归法作为参比模型。在SPSS软件中进行逐步回归［17］，选择“数理统计——回归——线性回归”，将训练集每年的麦蚜最大虫株率作为Y值，表1所有气象因子作为自变量，在方法框中选择“逐步回归”作为分析方法，按照逐步回归结果，计算2007—2011年麦蚜最大虫株率。

1.6 模型验证方法

本实验选择模型拟合精度、平均绝对百分误差（MAPE）和均方误差（MSE）等评价指标对模型性能进行评价［18，19］。

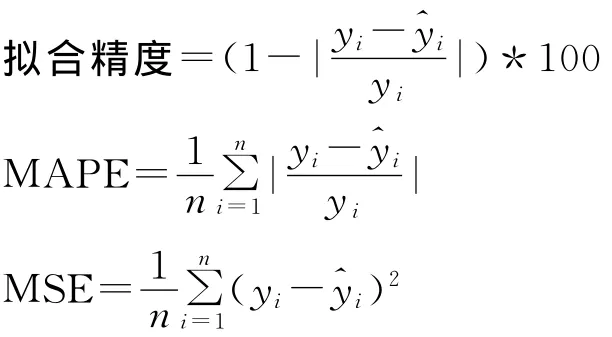
公式中，yi为最大虫株率的实际值，为模型的预测值，n为训练样本数。

2 结果与分析

2.1 基于BP神经网络和逐步回归法的1980－2006年麦蚜最大虫株率拟合结果比较

运用逐步回归法对麦蚜最大虫株率进行预测，得到多元线性方程为：

y＝21.936＋37.086x49－7.732x63＋3.159x32＋16.299x97

采用该方程对训练集进行拟合，得到1980—2006年麦蚜最大虫株率拟合图（图2）。

在逐步回归法对麦蚜最大虫株率的训练中，平均拟合精度为73.66%，最大拟合精度为99.87%，拟合精度超过90%的年份有8个；运用BP神经网络对1980—2006年麦蚜最大虫株率进行训练（图3），平均拟合精度为78.15%，最大拟合精度为99.16%，拟合精度超过90%的年份有11个，说明这两个模型都基本体现了麦蚜最大虫株率的发展规律。由于BP神经网络模型有较强的处理非线性问题的能力，因此其拟合效果略好于逐步回归。BP神经网络基于经验风险最小准则，其拟合效果取决于样本数的多少，训练样本越多，拟合精度越高，预测准确率越好，模型越稳定；当训练样本过小时，往往训练拟合精度高但预测效果差，易于出现过拟合现象。

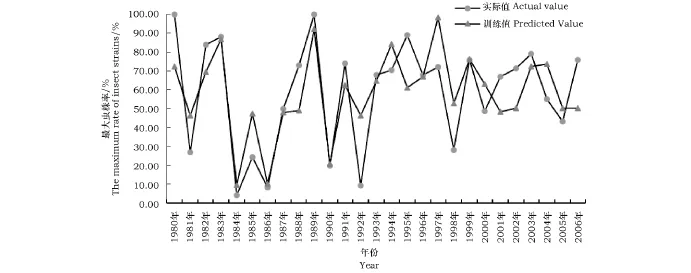
图2 逐步回归法对麦蚜最大虫株率的拟合结果Fig.2 The simulation effect of study by stepwise regression method

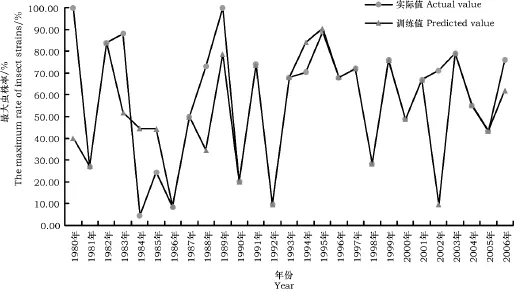
图3 BP神经网络训练拟合结果图Fig.3 The simulation effect of study by BPNN

2.2 基于BP神经网络和逐步回归法的2010—2011年麦蚜最大虫株率预测结果比较

比较BP神经网络和逐步回归模型的拟合精度和性能可得出（表2～表4）：

（1）BP神经网络的平均预测精度明显高于逐步回归，BP神经网络的平均预测精度为96.09%，逐步回归法平均预测精度为75.74%。BP神经网络对麦蚜最大虫株率的预测非常准确，5年的预测结果中3年超过95%。逐步回归法的预测结果较差，只有2009年预测准确率为99.01%，2010年预测准确率最低，只有34.85%，主要是由于逐步回归采用的是线性处理方法，麦蚜的发生受到气象因子、自身生长发育、寄主生长发育、天敌等多种因素影响，逐步回归法不能很好的处理非线性问题。

（2）比较两种模型的均方误差（MSE），BP神经网络模型的MSE值明显小于逐步回归，其预测的均好性高于逐步回归，表明其稳定性优于逐步回归法。

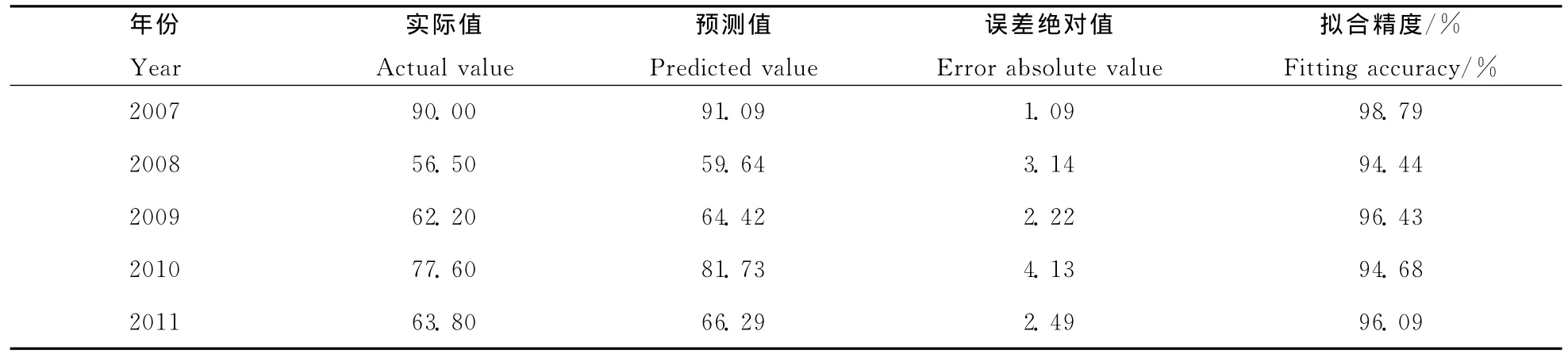
表2 BP神经网络预测结果Table 2 The prediction results of BPNN

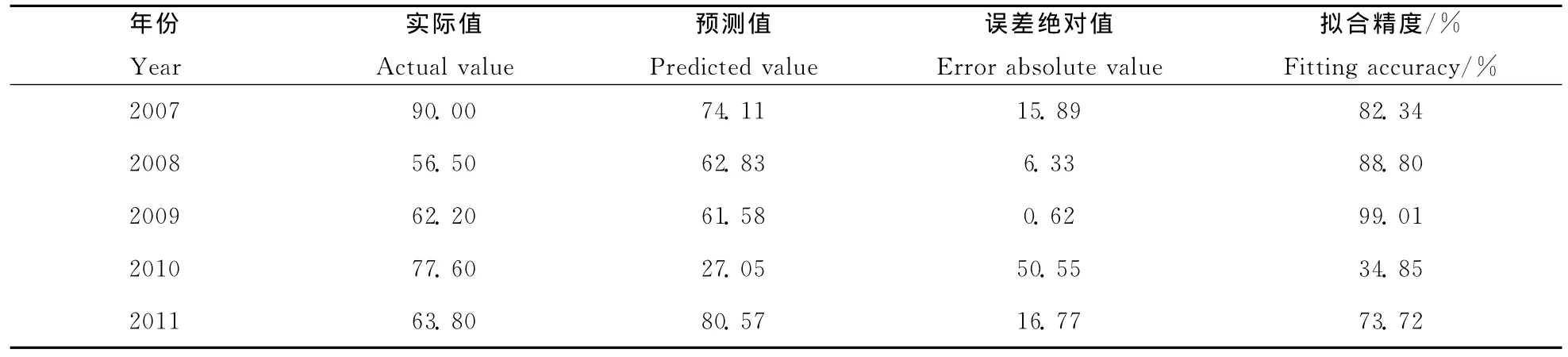
表3 逐步回归预测结果Table 3 The prediction results of stepwise regression method

表4 BP神经网络和逐步回归预测模型比较Table 4 Comparision of BPNN and stepwise regression method performances

3 讨论与结论

害虫发生是一个非常复杂的非线性过程，受到各种因素的影响，要建立准确且稳定的预测模型具有一定的难度。本实验建立了BP神经网络对麦蚜最大虫株率的预测预报模型，并与逐步回归法的预测精度和稳定性进行了比较。结果表明，BP神经网络的预测效果总体好于逐步回归，主要是由于其处理非线性问题的能力、良好的自学习、自组织和自适应性、良好的推广能力。在取得影响害虫发生且相当数量气象因子的基础上，此方法可较为准确的预测不同地区的病虫害发生情况。

但运用BP神经网络在病虫害预测预报中的研究较少，还存在许多亟待解决的问题。例如，本实验中没有考虑麦蚜越冬基数、天敌、寄主、防治措施等因素的影响，可通过进一步实验对这些因素做定性定量分析后进入建模过程。如何更准确的确定神经网络隐含层节点个数；当样本量过大时，由于神经网络学习了过多的样本致使输出模型不能反映样本内含的规律，超出了学习的度，易出现过拟合现象，如何选择样本数量的问题。下一步，可尝试对气象因子采用逐步回归法、主成分分析法等进行筛选；采用交叉验证法、试凑法等对神经网络的初始参数进行优化，以建立预测更加准确的神经网络预测预报模型。

［1］张孝羲，翟保平，牟吉元.昆虫生态及预测预报［M］.北京：中国农业出版社，1985：205－207.

［2］马飞，许晓风，张夕林，等.相空间重构与神经网络融合预测模型及其在害虫测报中的应用［J］.生态学报，2002，22（8）：1297－1301.

［3］王洪亮，王丙丽，李朝伟.害虫综合治理研究进展［J］.河南科技学院学报（自然科学版），2006，34（3）：40－42.

［4］张永生.害虫预测预报方法的研究进展［J］.湖南农业科学，2009，24（7）：77－79.

［5］陈恩会，王炜，张建军.BP神经网络在病虫预测预报中的应用简介［J］.湖北植保，2012，129（1）：41－44.

［6］王国昌，王洪亮，吕文彦，等.基于人工神经网络的害虫预测预报［R］.第二届亚太地区信息网络数字会议报告，2011：110－112.

［7］欧钊荣，谭宗琨，苏永秀.BP神经网络模型在甘蔗绵蚜虫发生发展气象等级预报中的应用研究［J］.安徽农业科学，2008，36（21）：9141－9143，9152.

［8］唐建军，王映龙，彭莹琼.BP神经网络在水稻病虫害诊断中的应用研究［J］.安徽农业科学，2010，38（1）：199－200，204.

［9］曹雅忠，尹姣，李克斌，等.小麦蚜虫不断猖獗原因及控制对策的探讨［J］.植物保护，2006，32（5）：72－75.

［10］印毅.麦蚜种群的发生为害与主要影响因子分析［D］.扬州：扬州大学，2004.

［11］罗长寿，左强，李保国.基于遗传算法的人工神经网络模型在冬小麦根系分布预报中的应用［J］.应用生态学报，2004，15（2）：354－356.

［12］陈明.MATLAB神经网络原理与实例精解［M］.北京：清华大学出版社，2013：156－191.

［13］张映梅，李修炼，赵惠燕.人工神经网络及其在小麦等作物病虫害预测中的应用［J］.麦类作物学报，2002，22（4）：84－87.

［14］朱大奇.人工神经网络研究现状及其展望［J］.江南大学学报（自然科学版），2004，3（1）：103－109.

［15］Gang Liu，Xuehong Yang，Yingbing Ge，et al.An Artificial Neural Network－based Expert System for Fruit Tree Disease and Insect Pest Diagnosis［R］.IEEE International Conference on Networking，Sensing and Control.2006：1076－1079.

［16］傅荟璇，赵红，王宇超.MATLAB神经网络应用设计［M］.北京：机械工业出版社，2010：193－208.

［17］吴骏.SPSS统计分析从零开始学［M］.北京：清华大学出版社，2014：302－305.

［18］向昌盛，周子英.ARIMA与SVM 组合模型在害虫预测中的应用［J］.昆虫学报，2010，53（9）：1055－1060.

［19］李启权，王昌全，张文江，等.基于神经网络模型和地统计学方法的土壤养分空间分布预测［J］.应用生态学报，2013，24（2）：459－466.