有限水深中破损船舶的运动与波浪载荷研究

冯乾栋，胡嘉骏，杨鹏，张凡

（中国船舶科学研究中心，江苏无锡214082）

有限水深中破损船舶的运动与波浪载荷研究

冯乾栋，胡嘉骏，杨鹏，张凡

（中国船舶科学研究中心，江苏无锡214082）

由于有限水深中船舶搁浅和触礁等严重破损事故频发，为了减少事故的发生，对有限水深中船舶破损后的运动及波浪载荷的研究显得十分必要。文章基于三维势流理论，引入有限水深自由面Green函数，在频域内使用奇点分布法对一艘首部破损进水的散货船在有限水深中的运动与波浪载荷展开了计算，并根据劳氏船级社规范做了短期预报。短期预报结果表明，该散货船破损进水后，船体所受垂向和水平波浪弯矩均比破损前有明显增加，且在较浅水深中变化更为显著。

有限水深；Green函数；载荷；非正浮；破损

0 引言

随着船舶科学技术的快速进步，单艘船舶的装载吨位以及造价越来越高，其安全性以及生命力也变得愈发重要。由于操纵失误、风浪等诸多因素，船舶在海上的事故时有发生。其中，搁浅和触礁等严重的破损事故常发生在有限水深海域中，这些事故对于船员以及货物的安全构成了严重的威胁。在1995年，27600 DWT的Sea Prince号超大型油轮在有限水深海域中搁浅,虽然该油轮被成功浮起,但由于外载荷的作用使得船体破损结构进一步破坏，最终在拖航中沉没。鉴于船舶在有限水深海域多发事故的事实，对于有限水深中破损后船舶的运动以及波浪载荷的研究是十分有意义的。

过去关于破损船舶波浪载荷的研究都是在无限水深中展开的，例如Lee等[1]根据二维线性势流理论，考虑船体多种破损情况，使用了源汇分布法求解了破损后非对称剖面的二维辐射和绕射流场，利用切片理论计算了船体水动力系数，预报了船舶破损后的波浪载荷。吴明远[2]基于三维线性势流理论，采用三维面元法在频域内计算了船体波浪激励力，求解了横倾船舶6自由度的运动。青兆熹[3]在前者基础上使用CFD技术考虑了破口交换水的粘性影响，研究了破损船舶的运动与波浪载荷。

为研究有限水深中破损船舶运动与波浪载荷，对积分形式的有限水深Green函数数值计算展开研究，使用Fortran语言编写了有限水深Green函数计算内核，在频域内基于三维奇点分布法对有限水深中的破损船舶展开水动力预报。考虑船舶前部发生第一类舱室破损的情况，对一艘零航速的破损散货船在波浪中的运动与波浪载荷展开了计算。计算结果表明，散货船破损后，垂向与水平波浪弯矩均有增加，并且在较浅水深中变化更为显著。

1 破损船舶运动与载荷预报

1.1 三维奇点分布法求解速度势

根据线性三维势流理论，假设流体为均匀、不可压缩、无粘并无旋，零航速船舶在稳定状态下做以频率ω随时间简谐变化的6自由度刚体运动[4]：

式中：（j=1，2，3，…，6）为复数振幅，依次指纵荡、横荡、垂荡、横摇、纵摇和首摇。

单位波幅的绕射势φD和j运动模态单位复速度辐射势φj满足下列定解条件[9]：

根据三维奇点分布法，方程（2）的解φj则可以使用格林函数在湿表面上的积分表示为：

为求解σ（q），可将船体湿表面近似离散成n个小平面四边形，取每一块的几何中心点为控制点，计算出每个控制点处的单位法向量ni。如果每个单元足够小，则可将每个单元上的σj视为常量，即，σji，物面方程就可离散为：

于是，关于σ（q）的积分方程便转换为n个离散量σi的n维线性方程组，通过求解线性方程组，即可解得每个单元上的σi分布。

另外，在计算完整的正浮船舶时，利用湿表面对称的条件，只需计算船体一侧湿表面的单元（即n/2个）即可。与正浮的船舶不同，破损后倾斜的船体由于不再正浮，湿表面左右不对称，所以在展开计算时，必须对船体整个湿表面划分单元进行求解。

1.2 有限水深Green函数的数值计算

准确计算Green函数及其偏导数是计算有限水深中流场速度势的关键。与无限水深Green函数相比，有限水深Green函数有其更为复杂的积分表达式与奇异性。本文使用了积分形式的有限水深Green函数[8]：

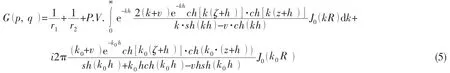
其中：h为水深，（x，y，z）为场点坐标，（ξ，η，ζ）为点源坐标。

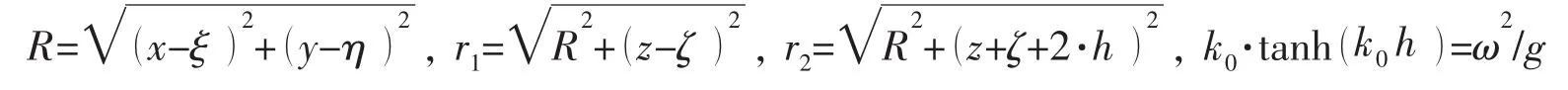
奇异积分是Green函数计算中的难点，将（5）式中主值积分项记为G0，则Green函数偏导数的主值积分项可以表示为：

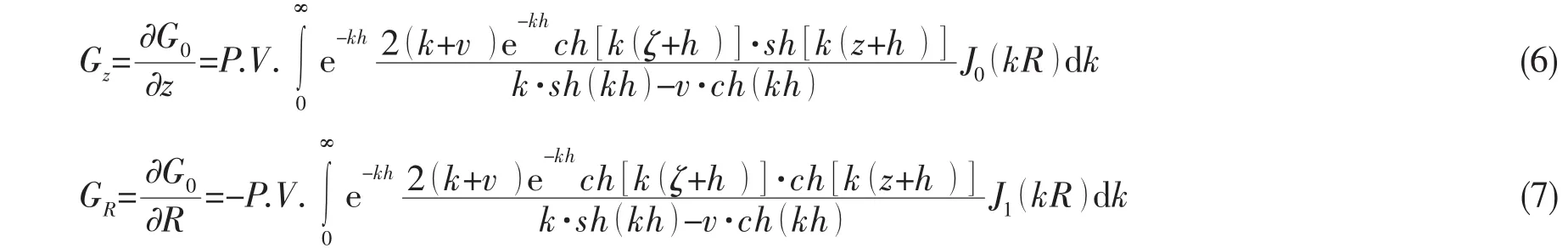
对于上述G0、Gz两项的计算，本文采用了文献[5]的方法。以G0为例，先进行配分子约分转换：

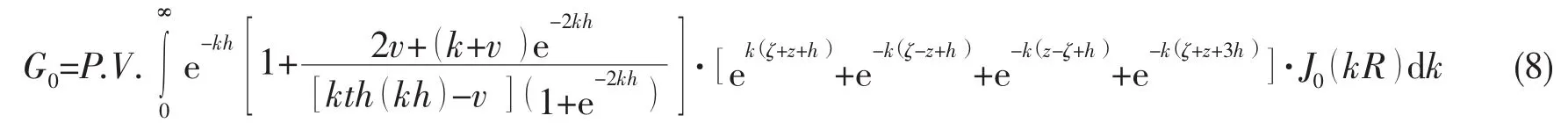
将（8）式展开，其中不带奇异项的积分以及奇异项积分分别可以表示为（9）、（10）式：

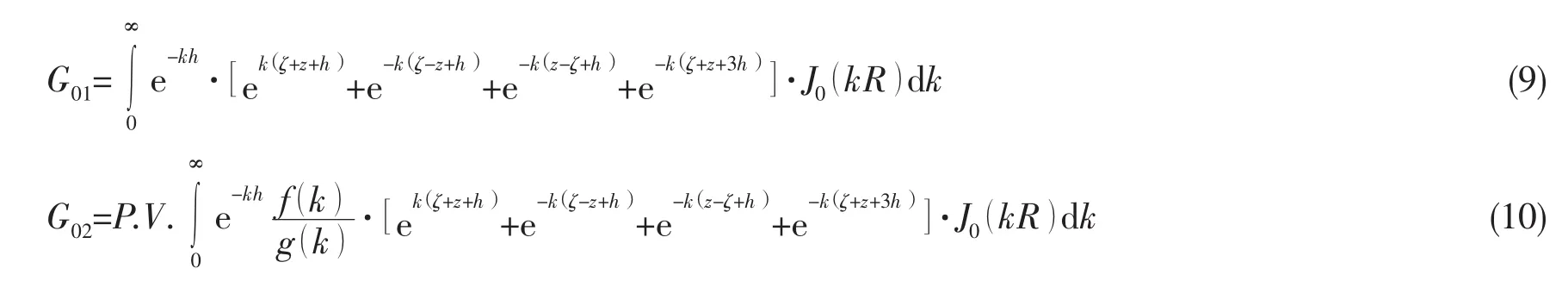
f（k）=2v+（k+v）e-2kh，g（k）=［kth（kh）-v］（1+e-2kh），（9）式可以通过J0的拉普拉斯变换式直接转换计算，（10）式则转换成Guass-Laguerre积分[9]与无限水深格林函数的主值积分[6]进行计算。

对于GR项，本文在文献[5]的方法基础上做了改进，通过直接对G01、G02求导进行计算：

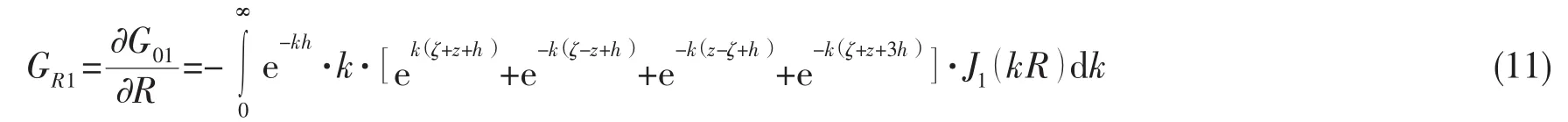
（11）式同理可以通过J1的拉普拉斯变换式直接转换计算。

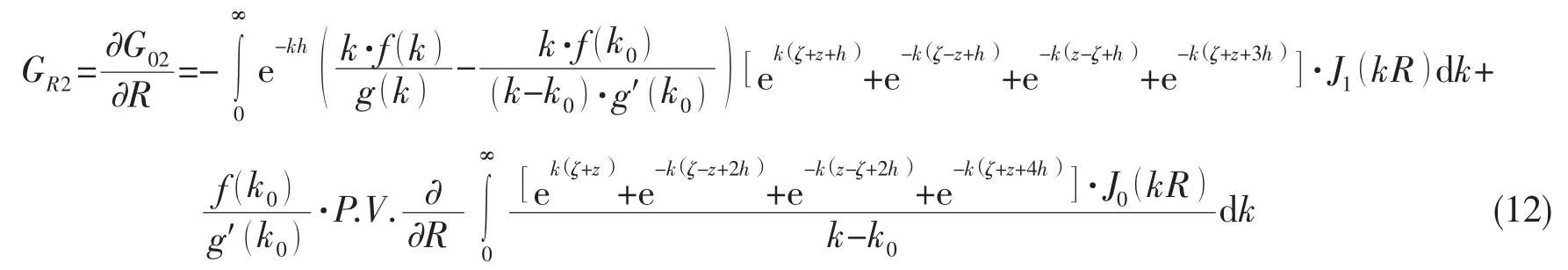
（12）式的第一个积分可以通过Guass-Laguerre积分来计算。第二个积分为主值积分，则通过无限水深的格林函数主值积分求偏导数来直接计算：

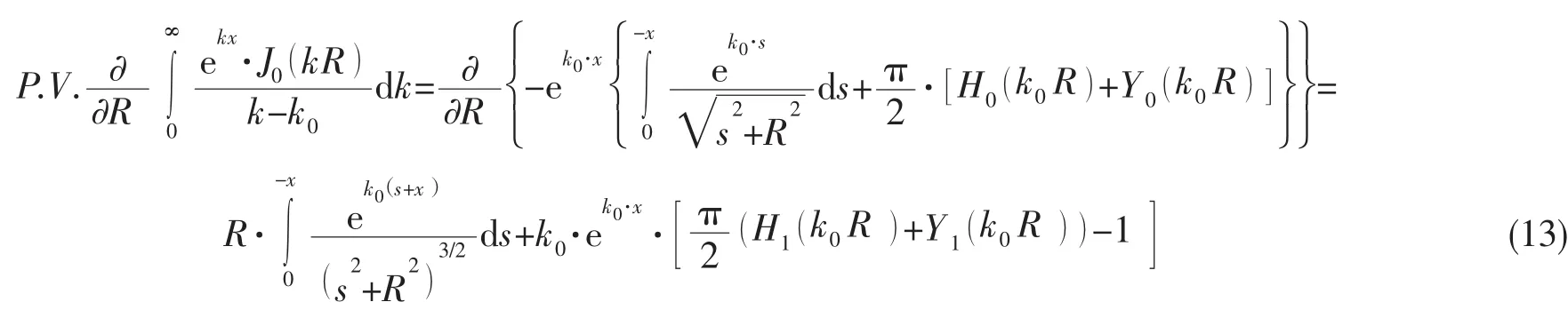
通过以上计算方法，可以有效地解决有限水深Green函数的奇异积分，避免了传统方法计算的失真问题。

1.3 破损船体在规则波中的运动与载荷计算根据刚体动力学，在频域内可建立船体6自由度运动方程：

式中：［M］矩阵为质量矩阵，［C］矩阵为静水回复力矩阵，［A］、［B］分别为附加质量矩阵以及附加阻尼矩阵，fw为波浪激励力。

由于船舶破损后具有一定横倾，船体质量分布、静水浮力不再关于中纵剖面对称，所以破损船运动方程中的质量矩阵［M］与静水回复力矩阵［C］与破损前有所不同。

非正浮破损船舶的质量矩阵［M］为：

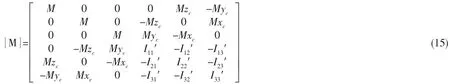
式中：M为船舶总排水量；（xc，yc，zc）为船体破损后的重心坐标；Iij′为船体破损后的质量惯性矩。

完好的船舶由于水线面左右对称，静水恢复矩阵中有5项不为零，而非正浮破损船的水线面不再对称，其静水回复力矩阵［C］中有9项不为零：

式中：Awp为水线面面积；Sx为水面线对x轴的静矩；Sy为水面线对y轴的静矩；Jxy为水面线对原点的静矩；hx为横稳性高；hy为纵稳性高。

波浪激励力fw可通过（17）式计算：

式中：φI、φD分别为入射波速度势、绕射势，ρ为水密度，ω为波浪频率。

通过（3）式求解得到6自由度运动后，船舯剖面处的波浪载荷Q可以通过（18）式计算：

式中：p为各面元处的波动压力，波动压力可通过各面元处的速度势来求解。

2 数值计算与对比分析

以一散货船为算例，基于上述方法改进自编程序wf3d，计算了破损后该船破损后在规则波中的运动以及载荷。该船破损前的主要参数如表1所示。

假设目标船舶在压载工况下航行于有限水深海域中，由于发生触礁或者搁浅事故，船体前部出现第一类舱室破损（如图1所示），破损舱室整体处于水线以下，舱室破损后海水充满整个舱室，所以本文不考虑海水晃荡的作用。假设破损导致船首部进水5 500 t，船体由于舱室破损进水产生倾斜。由初稳性公式计算可得船体平均吃水7.63 m，左倾3.94°，纵倾0.62°。如图1所示，在Patran中建立破损后的船体湿表面模型并划分网格，网格数为900。

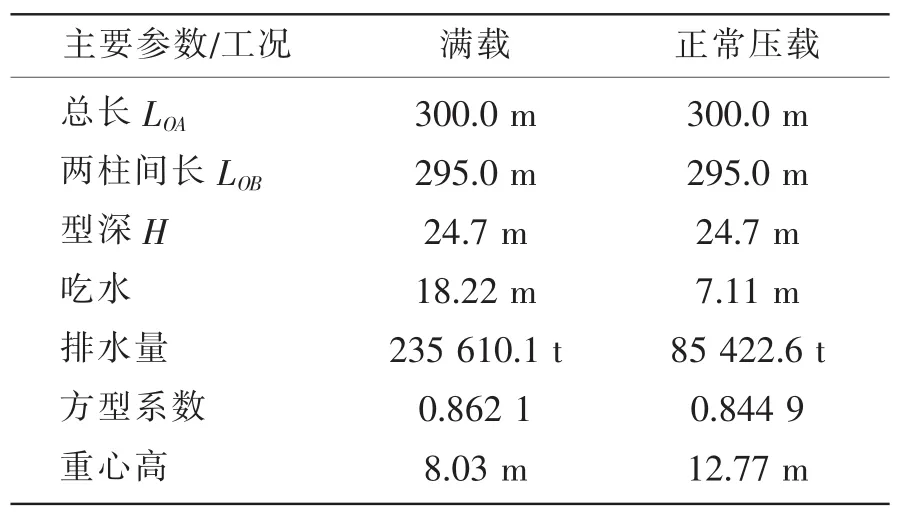
表1 散货船主要参数Tab.1 Bulk carrier’s main parameters

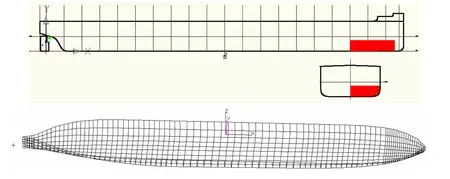
图1 船体舱室破损进水示意图和船体湿表面网格模型Fig.1 Hull’s damaged and flooded compartment and the grid model of hull’s wet surface

2.1 数值方法验证

为验证本文对有限水深Green函数、非正浮破损船舶运动响应计算方法的有效性与准确性，将自编程序wf3d计算结果与Wadam程序计算结果做了对比。图2中分别为零航速的破损船体在水深H= 20 m、50 m、80 m、100 m和300 m中顶浪下的垂荡以及纵摇运动响应传递函数。从图中可以看出本文计算结果与成熟商业软件Wadam的结果十分吻合，可见本文使用的有限水深格林函数计算方法和程序是可行的。

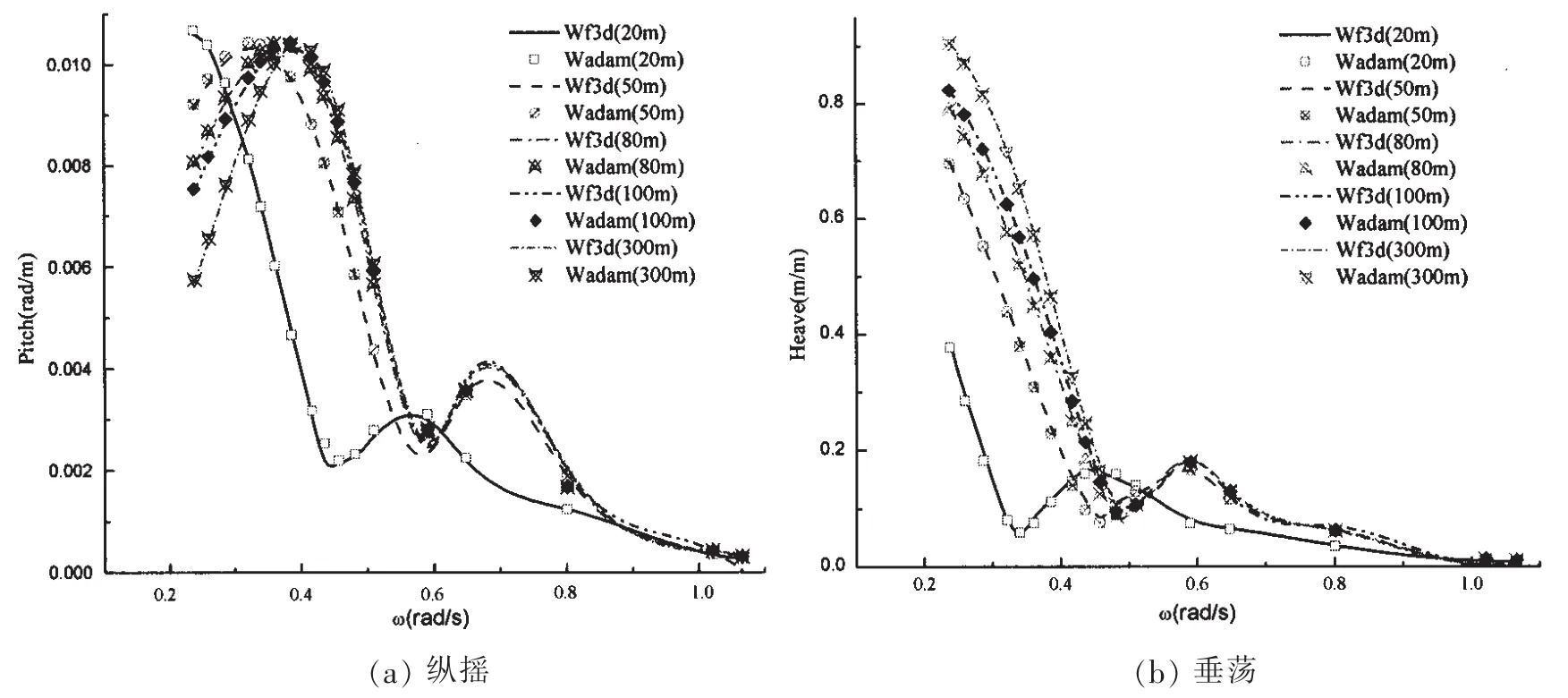
图2 顶浪下船体纵摇与垂荡响应传递函数Fig.2 RAOs of pitch and heave motion at head sea

2.2 破损对船体运动与波浪载荷的影响

为研究散货船破损前后在波浪中的运动与波浪载荷变化，本文对处于20 m水深的散货船展开计算。图3中（a）～（c）分别为顶浪下船体垂荡、纵摇与45°斜浪下横摇传递函数在破损前后的比较。图4中（a）～（b）分别为顶浪下船舯剖面的垂向波浪弯矩以及45°斜浪下水平波浪弯矩传递函数在破损前后的比较。从图3中可以看出散货船破损后垂荡、纵摇运动基本不变，横摇运动峰值增加。从图4中可以看出，散货船破损后两个方向的波浪弯矩的峰值均有增加，水平弯矩的增幅更为明显。

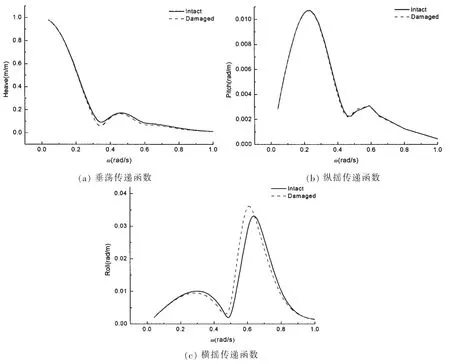
图3 运动响应传递函数比较Fig.3 Comparison of motion’RAOs

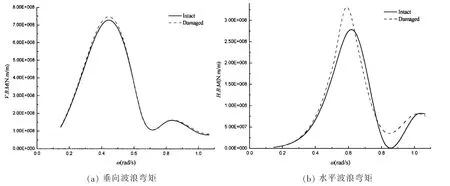
图4 波浪弯矩传递函数比较Fig.4 Comparison of wave bending moments’RAOs

根据英国劳氏船级社规范[7]，在校核破损船剩余强度时，破损船环境载荷预报的回复周期定为12小时。本文选取了JONSWAPS谱和5级海况（Hs=3.25 m，Tz=9.7 s），分别对不同水深中船体破损前后在顶浪下的船舯垂向波浪弯矩、45°斜浪下的水平波浪弯矩开展了12小时短期预报，计算结果如图5和表2所示。船体受损倾斜后，垂向、水平波浪弯矩短期预报值均明显增加，并且在较浅水深中变化更为显著，h=20 m时的垂向和水平波浪弯矩短期预报值增幅分别达到3.72%和30.42%。

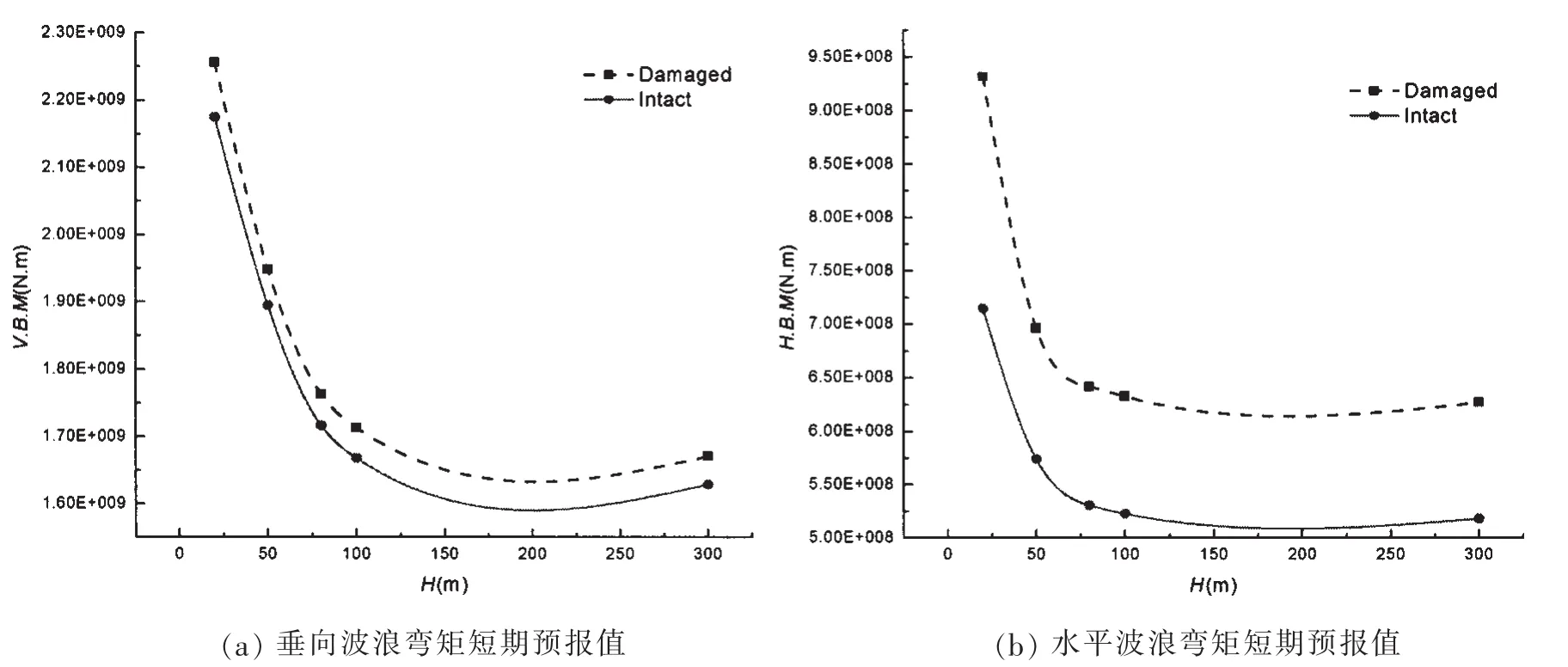
图5 不同水深下的波浪弯矩短期预报值比较Fig.5 Comparison of wave bending moments’short-term predictions in different depth

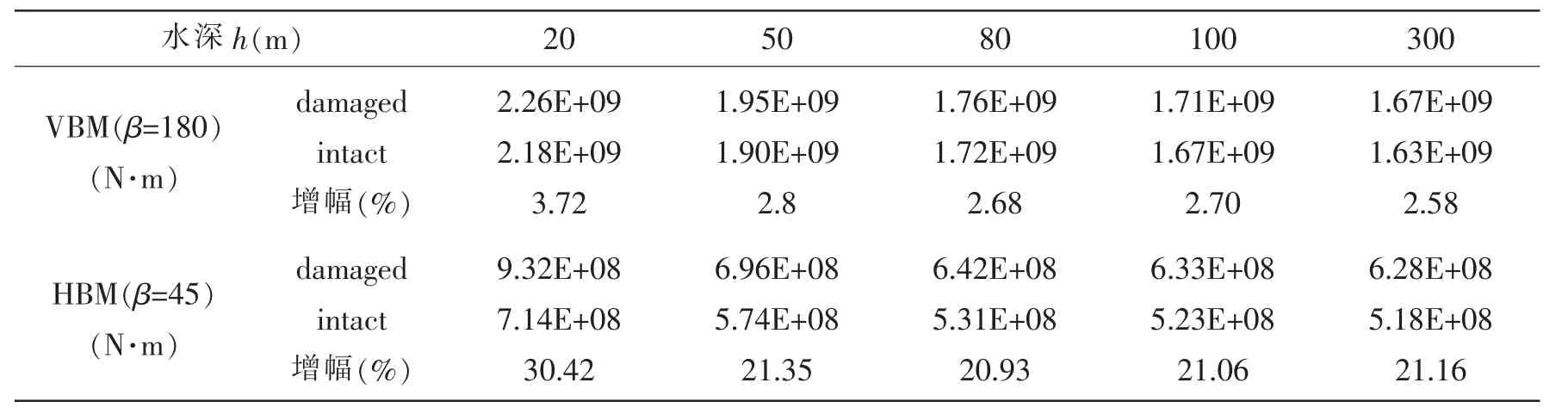
表2 波浪弯矩短期预报值比较Tab.2 Comparisons of the short-term predictions of wave bending moments

3 结论

由于船舶破损事故常发生在有限水深海域，本文使用了三维有限水深自由面Green函数，采用了三维线性频域方法对处于有限水深的一艘破损散货船在波浪中的运动以及波浪载荷展开了研究。通过数值计算，得到以下主要结论：

（1）散货船破损进水后，在规则波中垂荡、纵摇运动基本不变，横摇运动峰值增加；垂向、水平波浪弯矩的传递函数峰值均有增加，其中水平弯矩的增幅更为明显。

（2）根据劳氏船级社规范，对散货船顶浪下的船舯垂向波浪弯矩、45°斜浪下的水平波浪弯矩做了12小时的短期预报。预报结果表明，散货船受损倾斜后，垂向、水平波浪弯矩短期预报值均明显增加，并且在较浅水深中变化更为显著。

船体破损后波浪弯矩的增加对结构的剩余强度构成较大威胁，船体受损结构可能会进一步地被破坏。因此在校核破损船舶结构剩余强度时，考虑船体破损淹舱后浮态变化来计算其外载荷，这对破损船舶安全性以及生命力研究有着实际的意义。

参考文献：

[1]Lee Yongwong,Chan Hoisang,Pu Yongchang,et al.Global wave Loads on a damaged ship[R].Lloyd’s Register,2012.

[2]吴明远.破损船舶运动与波浪载荷的三维计算方法研究[D].哈尔滨:哈尔滨工程大学,2007. Wu M Y.Study of 3D calculation method of damaged ships’motion and wave load[D].Harbin:Harbin Engineering University,2007.

[3]青兆熹.破损船舶波浪运动载荷计算方法研究[D].哈尔滨:哈尔滨工程大学,2009. Qing Z X.Study of calculation method of damaged ships’motion and wave load[D].Harbin:Harbin Engineering University,2007.

[4]戴仰山,沈进威.船舶波浪载荷[M].北京:国防工业出版社,2007. Dai Y S,Sheng J W.Ship Wave Loads[M].Beijing:National Defense Industry Press,2007.

[5]刘日明,任慧龙,李辉.有限水深格林函数及其导数的改进Gauss-Laguerre算法[J].船舶力学,2008,12(2):188-196. Liu R M,Ren H L,Li H.An improved Gauss-Laguerre method for finite water depth Green function and its derivatives [J].Journal of Ship Mechanics,2008,12(2):188-196.

[6]孙伯起.低航速物体在波浪上的运动理论和波浪阻尼计算[R].无锡:CSSRC科技报告,1990.

[7]Lloyd Register(LR.).Rules For Naval Ships[S].2005.

[8]戴遗山,段文洋.船舶在波浪中运动的势流理论[M].北京:国防工业出版社,2008. Dai Y S,Duan W Y.Potential flow theory of ship motion in waves[M].Beijing:National Defense Industry Press,2008.

[9]Zhang S J,Jin J M.Computation of special function[M].A Wiley-Interscience Publication,1996.

Research on damaged ship motion and wave load in finite water

FENG Qian-dong,HU Jia-jun,YANG Peng,ZHANG Fan
(China Ship Scientific Research Center,Wuxi 214082,China)

For serious damaging accidents of ships,such as stranding,usually happen in shallow sea,it is very essential to carry out some researches on damaged ships’motion and wave load in finite water aiming at reducing accidents.In this paper,by using the free-surface Green function for finite water depth and 3D source distribution method,the motions and wave loads of a bulk carrier damaged in finite depths and flooded in bow are studied in frequency domain.And short-term predictions of wave loads are made according to rules of Lloyd Register.Numerical result shows that the damaged ship’s vertical and horizontal wave loads increase obviously,and the damage’s influence is more significant in shallow water.

finite depth;Green function;loading;non upright;damaged

U661.32

A

10.3969/j.issn.1007-7294.2015.04.005

1007-7294（2015）04-0381-08

2014-10-08

冯乾栋（1989-），男，硕士研究生，E-mail:fengqiandong@gmail.com；胡嘉骏（1965-），男，研究员。