论流量影响线法参数误差对计算流量的影响
■黄存国 张洪翠 彭 曦 文雨松
(1.南昌铁路局,南昌 330000;2.中南大学,长沙 410083)
1 引言
设计流量(或检定流量)是桥梁设计和桥梁维护的重要参数。计算流量的方法有很多,如依据流量观测值的数理统计方法;依据雨量观测值的经验公式法、推理公式法、铁路设计院法等[1-2]。
最近出现的流量影响线法也是一种依据雨量观测值的设计流量计算方法,它适用于中小桥涵的流量计算,因为这种方法不需要测量流域面积等外业资料而被广泛关注[3]。
流量影响线法的依据参数是雨量、涨水历时、退水历时、河道平均流速等。这些参数的准确度对正确计算设计流量和鉴定流量影响程度具有显著影响。因此本文就各因素误差产生的影响做出分析和研究,所得结论可供桥涵水文勘测参考[4]。
2 流量影响线法简介
2.1 流量影响线法的基本原理
流量影响线法将单位时段内的降雨量Ri看成列车轴重Pi,将桥位涨水历时t1看成简支梁应力计算点到左支座的距离L1,将桥位退水历时t2看成简支梁应力计算点到右支座的距离L2。这样利用雨量Ri求流量Q 的水文问题,就变成了利用简支梁应力影响线加载求应力的力学问题[3]。流量影响线法的计算式见式(1),加载过程如图1∶

图1 流量影响线加载示意图

式中,Ri—第 时段标定洪水雨量值;
Q′b(t)—t 时洪水雨量系列桥址断面处流量;
Cu(i)—t 时刻第i 时段标定雨量对应流量影响线纵标,对未进入或已移出部分取Cu(i)=0。
2.2 流量影响线法的标定
由结构力学可知,使用简支梁应力影响线前,需要确定影响线的最大竖标Ymax。可以根据简支梁的截面模量等参数计算结构力学中影响线的最大竖标Ymax,这是理论标定法。但最常用的方法是将一台机车置于桥梁上,实测其最大应力,然后反算得到Ymax,这是实验标定法。
同样可以利用实验法确定流量影响线的最大竖标Cumax。
取一次洪水为标定洪水,可以实测这次洪水的最大流量Qb,同时实测引发这次洪水的雨量系列R1,R2…,Ri…Rn。
假定式(1)中的流量影响线峰值Cumax=1,将R1,R2…Ri…Rn当作移动荷载系列,在流量影响线上加载,按式(1),可以计算出Q′b。
流量影响线峰值的标定值∶

2.3 利用流量影响线计算检定流量
若式(1)中雨量系列为设计频率或检定频率对应的暴雨量系列,并利用流量影响线峰值的标定值Cumax,就可以确定设计流量(或检定流量)Q[5]。
3 流量影响线法的参数
3.1 涨水历时t1
流量影响线法计算涨水历时,本着计算过程简单、计算结果可靠的原则,采用下列式(1)进行计算[2]:

式中,t1——涨水历时(h);
L——流域中心到桥址的距离(km);
V——沿流程平均流速(m/s)。
3.2 退水历时t2
涨水历时t1确定后,退水历时t2借助涨、退水历时之比确定。通过对瞬时单位线和广东省综合单位线简化分析,结合中小流域的水文特性,并以江西省流域实测资料作参照,制定了中小流域涨、退水历时之比t1∶t2的选取标准(详见参考文献3):对于山区陡峭、植被很差的小流域,可取t1∶t2=1∶3;平原区坡度较缓、流速较慢、植被较好的中等大小流域,可取t1∶t2=1∶5[3]。
3.3 雨量荷载R
雨量荷载R1,R2…Ri…Rn为实际测量数据,可以到铁路工务段或其它雨量站直接查得,分为标定雨量和计算雨量荷载,标定雨量荷载Rb是确定影响线峰值的关键参数,间接影响计算流量的准确性,计算雨量荷载Rn′是确定计算流量的直接参数。显然,雨量荷载R 的准确度直接影响最终结果。
3.4 标定流量Qb
确定Qb最好的方法是现场实测。
对于均匀稳定流河段,可以根据标定洪水在河岸或其它参照物上留下的水痕高程Hs按谢才-曼宁公式确定[7],单式断面流量计算公式:

式中,Qb——流量(m3/s);
n——糙率;
ω——过水断面面积(m2);
I——桥前水面坡度(rad);
x——湿周(m)。
复式断面流量计算公式:

式中,ni—河床断面各部分糙率;
ωi—河床断面各部分过水断面面积(m2);
xi——河床断面各部分湿周(m);
i=1,2,3 分别代表左河滩、河槽、右河滩。
由此可见,如果现场实测标定流量,则涨水历时t1、退水历时t2、标定雨量Rb、雨量荷载Rb′、标定流量Qb是直接影响流量影响线法的参数。复式断面计算流量涉及参数多,本文分析的参数误差影响针对单式断面进行。
如果按照满宁公式计算标定流量,则涨水历时t1、退水历时t2、标定雨量Rb、雨量荷载Rb′、标定水位 是影响流量影响线法的参数。
4 勘测产生误差
流量影响线法需要利用流域参数,其中最重要的是河道长度L。按照现有的测量手段,不可避免产生误差。精度最高的方法是直接到现场,使用钢尺丈量,但这种方法需要较多的人力物力。
随着互联网技术的普及,有越来越多的地形图成果出现在网上。其中,使用最多的是“Google 地球”。可以在360 网页上免费下载“Google 地球”。利用“Google地球”的【标尺键】就可以测量河道长度。
图2 是外南线流墩河桥在“Google 地球”上测量河道的轨迹。表1 是五次测量此河道的结果。
表1 表明,测量结果的最大值是6.40 公里,最小值是6.23 公里,两者相差2.65%。
有必要研究参数测量误差对最后结果的影响。

图2 外南线流墩河桥的河道

表1 外南线流墩河桥的河道测量结果(km)
5 单参数敏感度分析
5.1 本文分析中的一般参数取值
本文采用单参数的敏感度分析,它类似于控制变量法,即保持其他参数不变,仅改变其中一个参数研究计算流量的误差。
本文分析中一般参数采用:降雨过程为均布雨量过程,雨量集度R=20(mm/h);降雨历时Tb=1(h);加载步长Dt=1/120(h);涨水历时t1=5(h);退水历时t2=10(h),标定洪水最大高程Hs=2(m)。
其中,雨量荷载简化成如下图3 所示的20 个集中荷载:

图3 雨量荷载示意图
5.2 涨水历时t1 误差对计算流量的影响
对于特定的桥位,涨水历时t1是个常数,但却是一个很难准确测量的常数,往往采用目测确定,不可能没有误差,显然这种误差对计算结果有一定的影响。本文在计算这种影响时,仅改变t1的大小,使其在±10%范围内波动,即t1为4.5~5.5(h),其它参数按本文分析中的一般参数取值。
计算涨水历时t1的上下波动对计算流量的误差,图4 为涨水历时t1的误差对计算流量Q 的影响图。

图4 涨水历时t1 的误差对计算流量Q 的影响图
5.3 退水历时t2 误差对计算流量的影响
对于特定的桥位,退水历时t2同样是个常数,但却是一个很难准确测量的常数,往往采用目测确定,不可能没有误差,显然这种误差对计算结果有一定的影响。在计算这种影响时,仅改变取t2的大小,使其在±10%范围内波动,即取t2为9~11(h),其它参数按“3.1 本文分析中的一般参数取值”取值。
计算涨水历时t2的上下波动对计算流量的误差,图5 为涨水历时t2的误差对计算流量Q 的影响图。
本文对外南线流墩河桥作了计算对比,对比计算中只改变化主河道长度,其它参数不变。当外南线流墩河桥的主河道长度取6.4 公里时,使用流量影响线法得出百年一遇流量为129.8 立方米/秒。当外南线流墩河桥的主河道长度取6.23 公里时,使用流量影响线法得出百年一遇流量为130.7 立方米/秒。两者相差0.7%。

图5 退水历时t2 的误差对标定流量Qb′的影响图
5.4 雨量荷载Rb 误差对计算流量的影响
雨量是从铁路工务段或其它雨量站获得的,受诸多因素的影响,可能存在误差,这种误差对计算结果有一定的影响。在计算这种影响时,分为标定雨量和计算雨量两种情况来考虑[7]。
标定雨量确定标定流量Qb′,由式(2)可知,Qb′直接决定影响线峰值Cumax,进而影响计算流量,根据计算过程分析可知,影响函数为反比例函数形式,Rb在±10%范围内波动,即取值18~22(mm/h),其它参数按本文分析中的一般参数取值。
计算标定雨量Rb的上下波动对计算流量的误差,图6 为标定雨量Rb的误差对计算流量Q 的影响图。

图6 标定雨量Rb 的误差对计算流量Q 的影响图
计算雨量Rb′按式(1)直接计算流量,影响函数为正比例函数形式,图7 为计算雨量的误差对计算流量的影响图。
5.5 标定流量Qb 的误差对计算流量Q 的影响
由式(2)可知,在确定流量影响线峰值Cumax时,标定流量Qb在分子上,对计算流量的影响函数为正比例函数,在上下波动时对计算流量的影响图的纵坐标对应误差值与图7 相同。

图7 计算雨量Rb′的误差对计算流量Q 的影响图
5.6 标定洪水最大高程Hs 误差对计算流量Q 影响
标定洪水最大高程Hs 由外业测量获得,受测量仪器精度、洪水时波浪大小的影响,可能存在误差,这种误差对计算结果有一定的影响[8]。Hs 对标定流量的影响是通过对湿周和断面面积来作用的,本文分析河道断面采用的是河底宽10m,坡度比m=1 断面形式,如下图8 所示:

图8 河道断面分析图
在计算这种影响时,Hs 测量误差是确定的,不随Hs 变化,但不同的Hs 取值对断面面积、湿周的计算误差不同,本文取Hs=2m 分析,仅改变Hs 取值的大小,使其在±10%范围内波动,取桥位处最大水深为1.8~2.2(m),其它参数按一般参数采用原则取值。图9 为标定洪水最大高程 的误差对计算流量Q 的影响图。

图9 标定洪水最大高程Hs 误差对计算流量Q 的影响图
若按照满宁公式计算标定流量,则Qb的影响转移到标定水位Hs。此参数误差对计算流量Q 的影响与图9 相同[9]。
6 基本结论
流量影响线各参数影响计算流量 的影响程度表2所示。
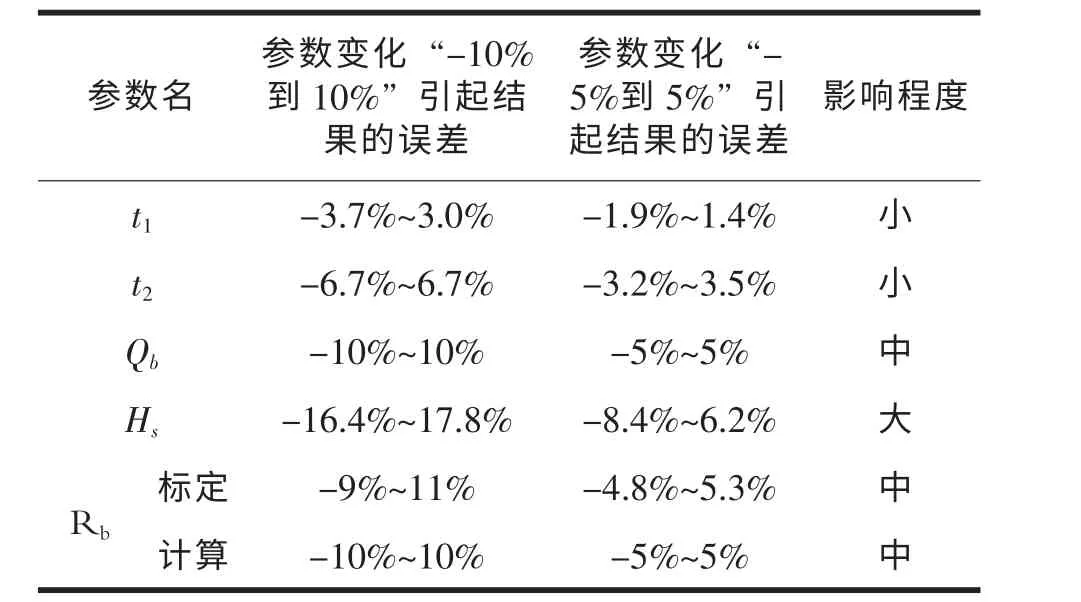
表2 Q 的参数敏感度分析汇总表
6.1 流量影响线是一种可用的方法
表2 表明,当流量影响线参数误差在“-5%到5%”以内时,流量影响线法的结果可用。
6.2 要特别控制标定洪水最大高程Hs 的精度
表2 表明,洪水最大水位高程Hs对结果的影响最大,其误差应严格控制在5%以内。其它参数对结果的影响不大,可以控制在10%以内。
7 结论
本文通过对流量影响线法的几个关键因素进行误差分析,得到明确且可提供指导意义的研究结果,为普及流量影响线法的运用提供依据。
当“标定洪水高程”的测量误差控制在5%以内,其它参数的测量误差控制在10%以内时,运用流量影响线法计算的设计流量能够满足准确性的要求。
在本文研究基础上,还可针对不同河床断面形式、不同雨量荷载统计周期等方面进行进一步的研究。
[1]文雨松.桥涵水文[M].北京:中国铁道出版社,2005.
[2]铁道部第三勘测设计院.铁路工程设计技术手册:桥渡水文[M].北京:中国铁道出版社,1999.
[3]李整.文雨松.流量影响线法及其在中小流域桥梁水文中的应用[D].铁道学报.2011(06).
[4]崔阳华,雷明锋.修正的桥梁水害水位单位线预警方法研究[J].铁道科学与工程学报,2012,9(3):68-71.
[5]刘洋宇,李整,文雨松.流量影响线法的可行性验证分析[J].铁道建筑,2011(3):23-25.
[6]张利平,张晓琳,徐霞,等.基于水文模型的雷达监测降雨量误差传递研究[J].水文,2012,32(1):13-16.
[7]胡嫄,李整,文雨松,等.基于流量影响线法的广东省中小桥换算雨量荷载系列研究[J].铁道科学与工程学报,2011,8(1):29-33.
[8]王强,文方针.中小流域桥梁设计流量的H-C-N 法[J].铁道科学与工程学报,2008,2008,5(2):42-45.
[9]贾借峰,赵井卫,陈客贤.曼宁公式及其误差分析[J].山西建筑,2010,36(7):313-314.

