上海市住房反向抵押贷款养老保险问题研究 ———产品定价与风险防范

□周 延 汪 伟 刘沁璐

华东师范大学



上海市住房反向抵押贷款养老保险问题研究
———产品定价与风险防范

□周 延 汪 伟 刘沁璐

华东师范大学

一、引言

作为一项新型金融产品，住房反向抵押贷款是否具有生命力，取决于其定价是否合理。由于住房反向抵押贷款借贷期限长，影响因素复杂，如利率、房价的波动、人均预期寿命的延长、道德风险等，定价一直就是住房反向抵押贷款的难点与核心，国内外学者围绕这一问题构建了诸多模型进行定量研究。目前主要是集中在固定利率的定价上。然而在现实经济中，利率是随着国家的经济运行状况不停地变动和调整的，所以需要从随机利率的角度来考虑定价问题。因此，考虑到利率的实际运行规律，本文运用Vasicek随机利率模型对上海市的住房反向抵押贷款产品进行定价，得出了开办住房反向抵押贷款的趸领金额和年金支付金额。

但是，住房反向抵押贷款是按揭贷款的一种逆向操作，由于时间跨度大，随着时间的推移，借贷双方的风险不断增加，尤其是贷款机构的风险在逐渐加大，因此，强有力的风险防范措施是住房反向抵押贷款健康发展的前提。虽然导致住房反向抵押贷款在实践中困难重重的原因有很多，但房屋价格的波动无疑是阻碍其成功推出的重要因素之一。尽管近年来我国总体房价呈上升态势，但仍不能忽视房价下跌给金融机构带来损失的可能性。作为以营利为目的的金融机构，能否有效规避房屋价格波动带来的风险，乃破解反向抵押贷款实践困境的关键。

综观国内外研究现状，不难发现，针对房价波动风险，美国等发达国家多采用资产证券化的方式进行风险分散，但由于中外证券市场所处的阶段不同，以及法律和监管条件的限制，我国实施抵押贷款证券化的条件并未完全成熟。鉴于此，本文从欧式期权的角度出发，采用Black-Scholes公式建立期权定价模型，设计出一款以反向抵押房屋作为标的物的看跌期权，对建立期权产品以规避房价波动风险进行了深入的探讨，并在最后提出对策建议，以期对上海市住房反向抵押贷款的实际开办有所借鉴。

二、基于随机利率模型的上海市住房反向抵押贷款产品定价

(一)定价模型的构建

1. Vasicek模型

设随机利率rt满足如下的随机微分方程

drt=k(θ-rt)dt+σdW(t)

(2.1)

式(2.1)中W(t)是一个标准布朗运动，k，θ为固定常数。Vasicek模型具有时间平稳性(即rt-rs的分布只依赖于时间差t-s)和均值回复性质。

2.年金支付公式

反向抵押贷款的定价模型与其领取方式有关，我们假设按期初终生生存年金的领取方式。借款人将自己拥有的住房以反向抵押的形式抵押给某个贷款机构，并按期取得现金收入。这种贷款机构的支付以及借款人的定期领取一直持续到借款人死亡。所以，在完全竞争市场中，考虑单个借款人一次性领取全部贷款的总额，根据精算学和收支平衡的原理有：

(2.2)

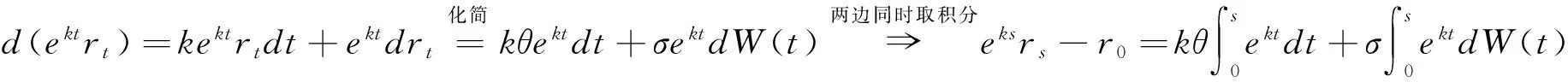
式(2.2)中各参数代表的含义为：

1.α表示房产的年增值率。由于我国各地区的城市化进程差异较大，房产价值的增值率在不同的地区呈现不同的趋势。有的地区房产价值增值较快，有些地区的房产价值增值较慢。因此，我们在反向抵押贷款的定价过程中，对房产价值的增值率不能一概而论，应该针对不同的地区采用不同的房产增值率。

2.β表示年折旧率。为了尽可能地反映真实情况，本文在建立定价模型时考虑到了房屋的折旧。

3.γ表示开办住房反向抵押贷款的其他费用占价值的比例。其他费用包括发起费、第三方费用、服务费和保险费等。发起费全部由借款人支付，保险费与住房反向抵押贷款是成比率关系的，其他还有如第三方为评估房屋价值和办理其他手续产生的费用。

4.H0表示借款开始时的房产净值，为了模拟计算的方便，假设H0=100万元。

6.ω为生命表上的最大年龄，为105岁。

然而，在实际操作中人们更倾向于年金支付的方式，所以根据金融产品定价的一般原理，即：

特定机构支付现金的年金终值=特定机构最终收回房屋的可变现净值

由此可以得到：

(2.3)

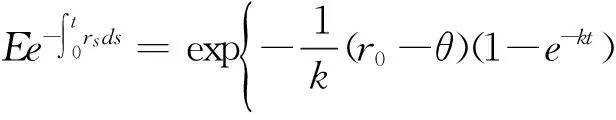
(2.4)

式(2.4)中rt是满足Vasicek模型式(2.1)的随机利率，即：

所以根据式(2.2)、(2.3)、(2.4)得出在Vasicek模型下的住房反向抵押贷款的年金支付公式为：

(2.5)

式(2.5)中rt，λ(t)同式(2.4)中的含义。

(二)数值模拟与计算

以上海地区为例，现考虑年龄分别为65岁、75岁和85岁的老年人开办住房反向抵押贷款的年金领取金额，利率由式(2.1)表示。下面讨论公式(2.5)中各个参数的取值问题：

1.年增值率α的取值

根据中国统计年鉴，2000年到2009年上海市商品住房价格如表1所示。由表1可知，上海市房产2000—2009年的平均增值率约为16%。

2.年折旧率β的取值

我国住宅寿命以70年计，采用匀速折旧法，每年的折旧率为1.43%。另外考虑到近年来房屋土地的价格不停上涨，应适当地调整房屋的折旧率，本文为计算方便暂取为1.25%。

3.开办费用占价值的比例γ的取值

由于我国目前尚没有开办住房反向抵押贷款的经验，所以对于开办业务的各项费用支出没有一个标准。但是美国的住房反向抵押贷款的业务开办较早，各项制度也比较完善，所以我们借鉴美国的经验，开办业务的各项费用支出γ=7.5%。

4.房产初值净值H0

为了便于计算，假设H0=100万元。

5.tpx的计算

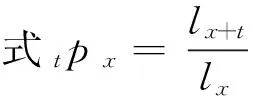
另外设r0=0.05，k=0.85，θ=0.09，σ=0.08，根据式(2.2)和各参数的取值计算一次性支付总额分别为L65=229.82(万元)，L75=162.47(万元)，L85=125.65(万元)。根据式(2.5)和各参数的取值计算终生生存年金的支付分别为A65=28.99(万元)，A75=27.88(万元)，A85=33.92(万元)。

表1 上海市2000-2009年房价增值率

资料来源：《中国统计年鉴》1999—2010年

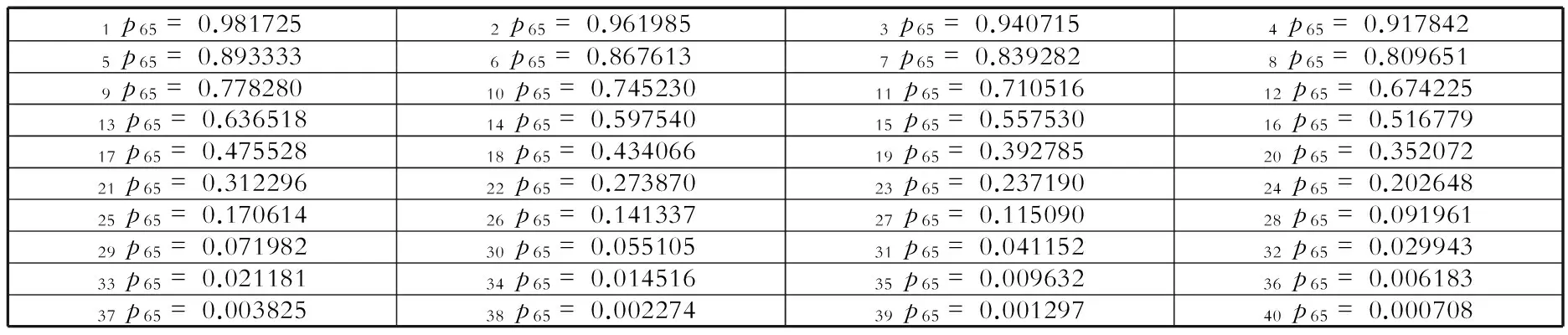
表2 t p65 的计算值

表3 t p75 的计算值

表4 t p85 的计算值

(三)数值模拟与计算结果分析

本文从保险精算定价方法出发，在固定利率模型的基础上进行进一步推广，将随机利率运用到定价模型中，从而得出了随机利率下的住房反向抵押贷款的模型。从年金支付模型的构建可以看出，利率和房屋价值波动率是影响年金支付额度的两个重要因素，所以在定价模型的构建中必须要考虑这两个因素对年金支付额的影响。由此也验证了用随机利率去代替固定利率来考虑住房反向抵押贷款的定价会更趋于合理的结论。最后对年金支付额进行了计算，得到了65岁、75岁和85岁三个年龄段的趸领金额分别为L65=229.82(万元)，L75=162.47(万元)，L85=125.65(万元)，年金支付额分别为A65=28.99(万元)，A75=27.88(万元)，A85=33.92(万元)。从上面的数值可以看出，由于房屋的增值额度随着存活的时间增大而增大，所以越早开办住房反向抵押贷款，其收益越大。另外，由于近年来房价增值较快也造成趸领金额和年金支付金额相对较大，这从某种程度上会对广大老年人办理这项业务产生激励作用。

三、上海市住房反向抵押贷款的风险防范——以房价波动风险为例

本文从欧式期权的角度出发，设计出一款以反向抵押房屋作为标的物的看跌期权，命名为反向抵押价值期权RMV(ReverseMortgageValue)。金融机构购买这种看跌期权后，享有在到期日将手中标的物按照履约价格卖给期权出售者的权利，从而规避房屋价格下降的风险。

(一)RMV期权模型的构建

1.模型构建

RMV期权的标的物为借款人的房产，该类房产价值可类比市场中二手房屋的交易价格。本文选取二手房交易价格作为参考数据，进行RMV期权的定价模拟。

本文使用Black-Scholes期权定价模型(以下简称B-S模型)为RMV期权定价。由于B-S模型条件限制，在使用该模型前需先进行房价数据拟合分析，验证其是否服从对数正态分布。此外，为简化问题，笔者假设该欧式期权不存在市场摩擦，且在有效期内无风险利率和金融资产收益变量恒定。由于反向抵押过程中的房屋投保人依旧拥有房屋使用权，故保险公司不享有该住房产生的收益，参考B-S无收益资产期权定价公式，RMV期权定价模型可表述如下：

2.参数设定

采集n个月二手房交易价格原始数据记为Pt(t取值范围1～n)。设期权执行价格为L，房屋价格收益率为rc，房价变动波动率为σ，无风险收益率为rf。

(1)执行价格L

B-S定价模型假设标的价值服从布朗运动。不妨基于伊藤引理建立期权的执行价格模型。

假定房产价格具有马尔科夫性，同时遵循一般化的维纳过程，即具有不变的期望漂移率以及方差率。则价格P的瞬时期望漂移率为rP，瞬时方差率为(rP)2，其Ito过程是：

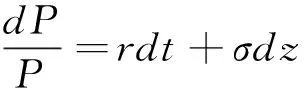
(3.1)

由于P服从几何布朗运动，可将其进行对数化变换。不妨定义G=lnP，假设G是P、t的函数G(P,t)，由Ito定理可得G遵循如下过程：

(3.2)

现在对G求导可知：

代入到式(3.2)得到G的过程为：

(3.3)

然后计算房屋执行价格模型的显性解。

假设在t至T时刻内对式(3.3)求解:

(T-t)+σ(T-t) 得：

(3.4)

式(3.4)即是式(3.3)房屋价格的伊藤随机微分方程的显性解，即RMV期权合约中的标的房屋执行价格L的值。

(2)收益率rc

(3)波动率σ

先计算连续复利收益率的均值：

再计算连续复利收益率的标准差，即波动率:

(4)无风险收益率rf

我国对于无风险收益率的选择没有统一的标准。一般选用短期国债收益率或者商业银行同期定期存款利率，本文选择银行同期定存利率作为无风险收益率。

3.基于Matlab的期权定价模拟与敏感性分析

在MATLAB命令窗口输入如下命令:

[cpricepprice] =blsprice(price,strike,rate，time,volatility,yield)

其中:

Price：标的资产在目前时点上的价格；Strike：期权到期日执行的价格；Rate：年化无风险利率,不考虑期限结构,并且连续计息；Time：以年为单位的时间计量；Volatility：标的资产价格波动率；Yield：期限存续期内, 标的资产年化的连续计息分红率；cprice：看涨期权价格；pprice：看跌期权价格。

程序运行后即可输出看涨期权与看跌期权的价格。

使用MATLAB对期权进行敏感性分析，分别计算六个敏感性指标，Delta、Gamma、Vega、Theta、Rho、Lambda。通过对期权的敏感性分析，可以从利率、房价变动、时间、波动性等众多不确定性因素中找出对期权价格影响较大的敏感性因素，并分析、测算其对价格的影响程度和敏感性程度，进而判断RMV期权对各项风险的承受能力。期权各项指标的评价标准如表5所示。

(二)实证分析过程

通过“上海市房地产交易服务网”采集并处理得到上海市2011年6月至2014年5月二手房交易均价数据，如图1所示。由于期权标的价格波动需服从布朗运动，我们要选取干扰较少情形下的价格波动，即排除由外部因素(如政策因素)导致的房价变动数据。由于2012年7月“沪六条”政策(2012年7月27日，上海市人民政府办公厅发布《关于进一步严格执行房地产市场各项调控政策的通知》，主要政策有：严格二套房认购标准，

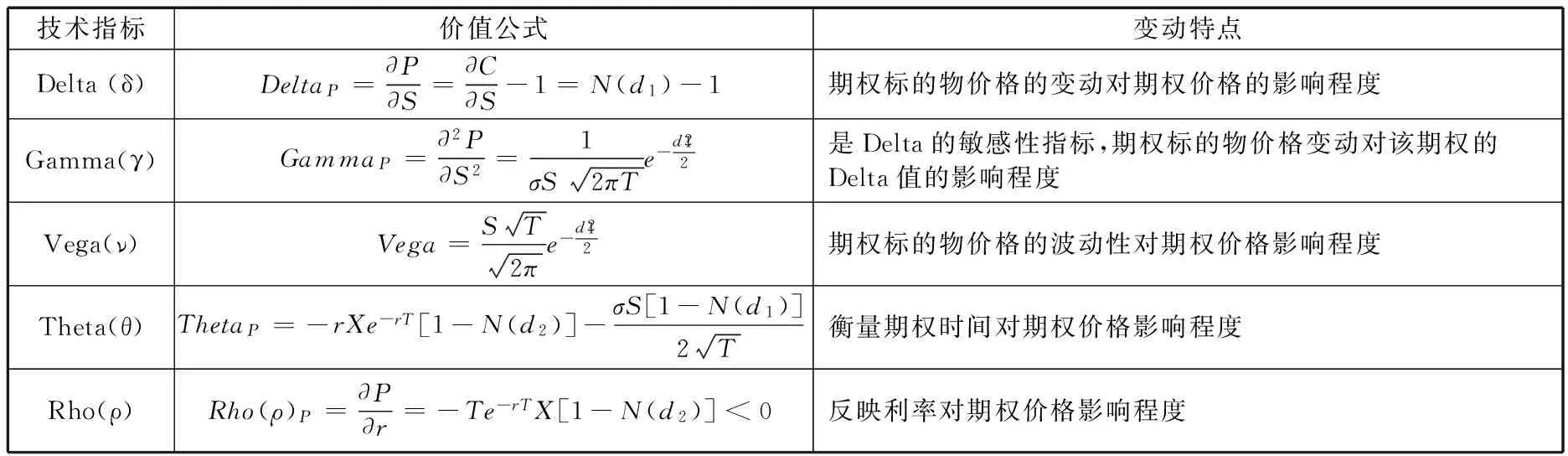
表5 期权敏感性分析技术指标

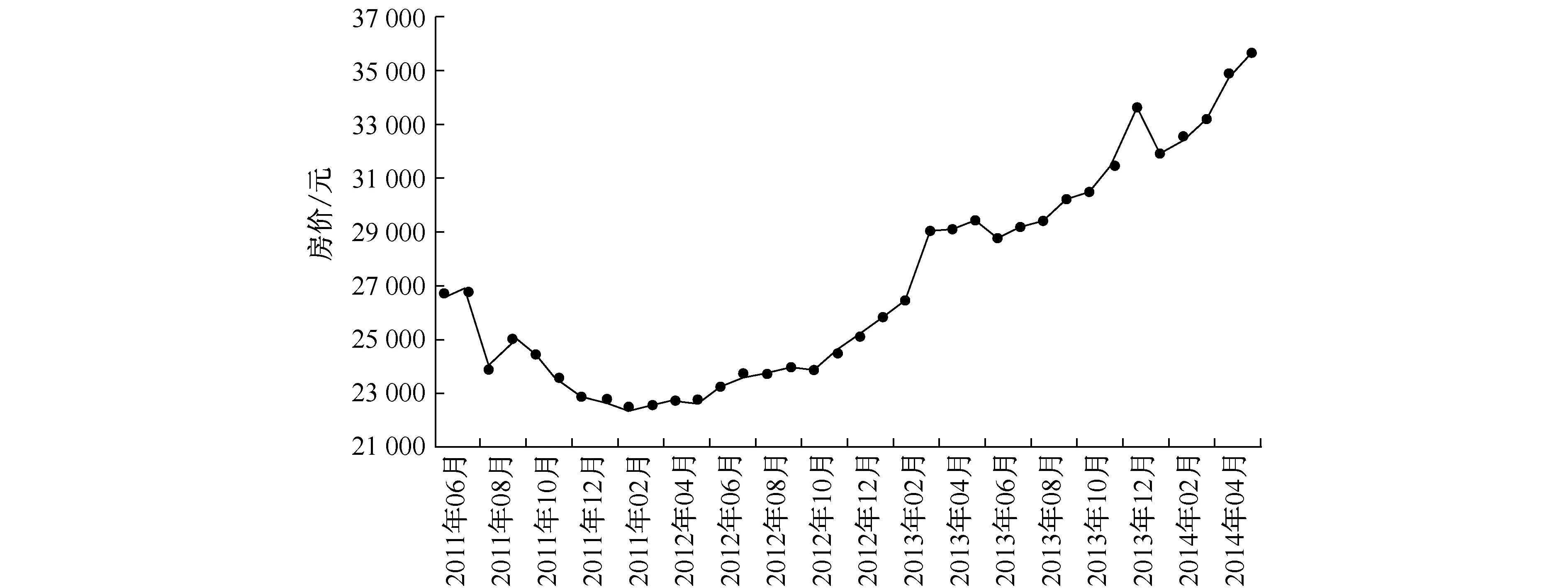
图1 2011年6月至2014年5月上海市二手房交易均价数据来源：上海市房地产交易服务网

严格差别化公积金贷款，加强合同签约环节监管，公寓式酒店严禁分套销售等，称为“沪六条”)的出台，上海市二手房价开始飙升，加之2013年3月的“国五条”政策(2013年2月20日，温家宝主持召开国务院常务会议，研究部署继续做好房地产市场调控工作，会议确定了五项国务院再出“国五条”抑制投机投资购房加强房地产市场调控的政策措施，称为“国五条”)，二手房价进一步呈现反常涨幅，无法反映正常房价波动，缺乏代表性与普遍性，因此本文选取2011年6月至2012年5月期间的数据进行期权定价模拟。

模型中的无风险利率采用我国2014年商业银行一年期定期存款利率，设为3.0%。首先假设存续期为1年。由式(3.4)计算得，执行价格为27370元。

根据B-S定价模型假设，房价应服从对数正态分布。使用Matlab的cftool拟合工具箱对已经对数化的12组房价数据进行正态分布拟合，得到图2。

图2显示上海市2011年6月至2012年5月期间的二手房价格大致服从对数正态分布。符合B-S模型假设。

使用Matlab软件进行如下计算：

由公式rc=log(Pt)-log(Pt-1)求出如下11组收益率：0.0041 -0.1129 0.0461 -0.0243 -0.0387 -0.0304 -0.0043 -0.0118 0.0051 0.0045 0.0026。

计算出收益率均值为-0.0145。

由11组收益率和均值求出波动率为0.0397。

根据以上数据，在Matlab中输入代码[cpricepprice] =blsprice(26710, 27370, 0.03, 1, 0.0397,0) 进行期权定价模拟。

输出结果为：cprice=500.4541pprice=351.5484

即欧式看跌期权在2012年5月时点上，以26710元/平方米为初始价格，设无风险利率0.03，波动率0.0397，行权价格为27370元/平方米，距离到期日还有12个月时的期权费为351.5484元/平方米。

图2 基于Matlab的房价数据正态分布拟合

与此类似，可利用该方法计算出以2012年6月为固定的到期时间，起始时间分别为2011年7月至2012年5月的各月，每个月购入RMV期权的期权费，结果如表6。

用Matlab对该期权进行敏感性分析，得到表7数据。

关于房屋价格的变化率。本次模型中Gamma绝对值较小，说明Delta随房价的变化很慢，即房价变动对期权价格的影响较小。Theta的数值表示如果将期权时间延长一年，RMV期权的价格会上升547.8365元。Vega值说明了当房屋价格波动率增加一个单位时，RMV期权价格增加10519.1元。Rho的数值在理论上显示了如果商业银行利率增加一个单位，RMV期权价格会下降12001.84元。

根据上述期权定价模拟结果，拟定出上海市反向抵押价值期权虚拟合约， 如表8所示。

(三)实证结果分析

首先，利用B-S公式构建期权定价模型，设置执行价格、收益率、波动σ等参数，并利用Ito过程等方法进行参数估计。采纳上海市二手房价格数据，使用Matlab对房价进行对数正态拟合并求解各项参数。从图1可以看出， 2011年6月至2012年5月上海市二手房价持续下跌，金融机构拥有的抵押房屋有贬值风险，若选择在2011年6月购买RMV看跌期权，由Ito过程求得的行权价格为27370元/平方米，则在2012年5月的交割日，扣除352元/平方米的期权费(由于该期权的期限较短，暂且忽略货币的时间价值)后，金融机构依旧可以减少4258元/平方米的损失，从而说明RMV期权能够起到规避房价下跌风险的作用。

其次，模拟出到期日同为2012年5月，但起始日期不同的期权价值，如表6所示。观察数据不难发现，由于房价下跌，当执行价格在27370元/平方米高位时，距离到期日越近，看跌期权的价值越高，但卖出看跌期权的风险也越大，故此时买卖双方的衍生品交易都应尤为慎重。之后通过Matlab对各指标的演算，分析了RMV期权对利率、时间、波动率等因素的敏感性程度。最终根据上述信息，模拟出“上海市反向抵押价值期权虚拟合约”，该合约可以为RMV期权的具体实施提供一定的参考。

当然，由于模型的设计环节存在一定的误差，本文定价方法的精确程度取决于我们假设的房价变化过程与实际的价格变化过程的吻合程度，在今后的研究中，还需要更多的数据对本文的模型予以验证和改进。

四、结论与建议

(一) 研究结论

1.定价是住房反向抵押贷款开办的关键和核心，考虑到利率的随机性，本文从随机利率角度出发，运用Vasicek模型建模，然后将其和保险精算定价模型结合起来得到一个具体定价公式，并以上海市为例讨论了模型中各个参数的取值，得出了上海市开办住房反向抵押贷款的趸领金额和年金支付金额，65岁、75岁和85岁三个年龄段的趸领金额分别为L65=229.82(万元)，L75=162.47(万元)，L85=125.65(万元)，年金支付额分别为A65=28.99(万元)，A75=27.88(万元)，A85=33.92(万元)。

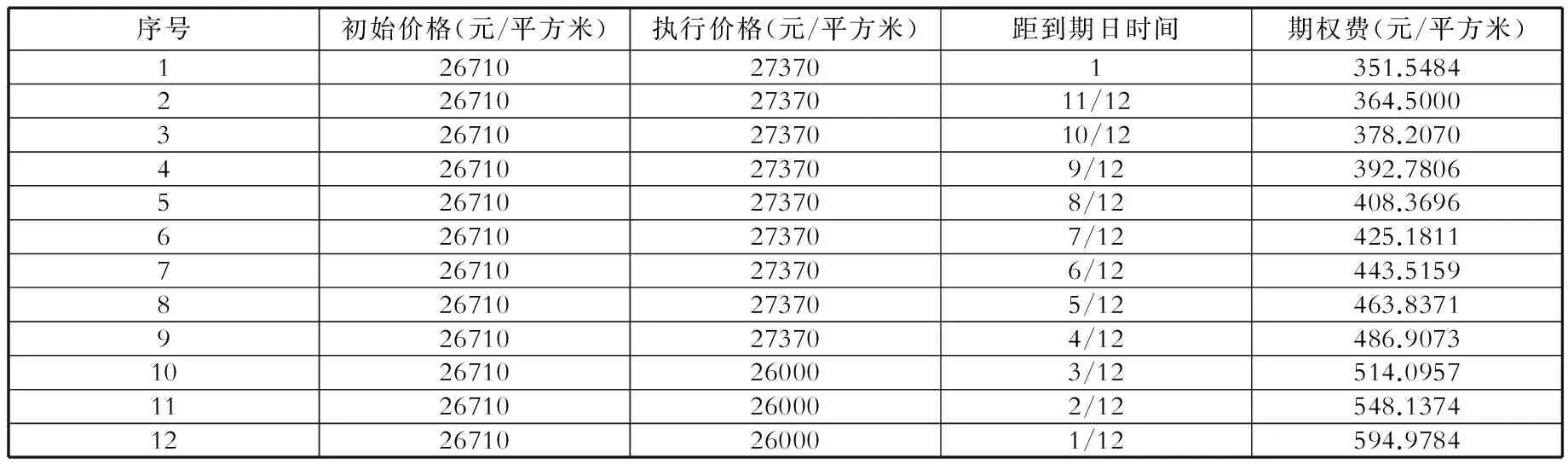
表6 Matlab对期权费的实验模拟结果

表7 RMV期权敏感性分析各指标数据

2. 鉴于住房反向抵押贷款业务持续时间长，影响因素复杂，本文以房价波动的风险为例，设计了一款反向抵押价值期权。首先，对于期权执行价格的确定，采用伊藤过程建模求解，以改良以往模型中直接设定行权价格的方式。其次，使用Matlab对原始二手房交易数据进行编程拟合，根据曲线走势判断标的物价格波动特性，验证其是否符合对数正态分布的假设，避免了前人研究中直接假设数据符合对数正态分布而导致的分析误差。再次，在期权定价模型完成后，利用敏感性参数分析RMV期权对各变量的敏感性程度，从而判断出其对于各项风险的承受能力，力求最大程度地实现期权定价方法的精确与实用，以达到有效规避反向抵押贷款风险之目的。

(二)政策建议

1.产品的准确定价是住房反向抵押贷款发展的核心

合理的定价是任何一项新产品取胜的关键，质优价廉是其驰骋市场的法宝。我国住房反向抵押贷款养老保险之所以风声大、雨点小，究其原因，一是这一产品在我国是新产品，缺乏定价的经验数据；二是其影响因素复杂多变，且属于长尾业务，这对目前的精算技术提出了挑战，也加大了产品设计、开发、定价的难度。但是，价格的高低关乎借贷双方的切身利益，尽管目前有诸多探讨，但均是在未来房价、利率、人的预期寿命等假设的基础上进行的，而我国的房价因素等很难预期其未来走势，这几成我国住房反向抵押贷款推出的死结。所以，要保持经济的平稳运行，不断完善资本市场，包括房地产市场，避免房价大起大落，在此基础上对各风险因素进行准确预测,充分考虑其波动对定价结果的影响，才能给出准确、合理而科学的定价，调动借贷双方积极性，促使住房反向抵押贷款成功推出并稳定发展。

2.完善金融和房地产市场，建立风险防范机制是反向抵押贷款长效发展的关键

由于反向抵押贷款期限长，影响因素多，运行机制复杂，牵涉部门多，任何一个环节出现问题均会影响其顺利推出和实施。但是由于利率、房价和人的预期寿命乃住房反向抵押贷款定价的主要因素，能否有效防范这三方面的风险是借贷双方参与反向抵押贷款的关键。但鉴于我国目前的利率没有完全市场化，房价也受政策性因素的影响，加之目前“二胎”等人口政策的调整，三者叠加导致定价的精准性大打折扣，因此，要借鉴反向抵押贷款发展成熟的国家的经验，加快房地产金融市场改革，减少人为干预，积极引进符合我国实际的融资工具和模式，建立良好的风险防范机制，这是我国反向抵押贷款长效发展的关键，当然，政府的支持也是反向抵押贷款发展不可或缺的因素之一。

表8 上海证券交易所(SSE)上海市反向抵押价值期权虚拟合约