基于冗余2 代小波局部梯度谱熵的轴承故障诊断

张 园 李 力

(①三峡大学科技学院，湖北 宜昌 443002;②三峡大学机械与材料学院，湖北 宜昌 443002)

滚动轴承在工业生产中应用非常广泛，其状态常影响整个设备的精度、可靠性与寿命［1］。冗余第2 代小波降噪能提供更丰富的特征信息可更好划分频带，但是存在频带错位和误差积累两类缺陷，改进的冗余第2 代小波包分解可克服这些不足［2-4］。梯度在信号检测和图像识别中得到了很好的应用，例如平均梯度反映图像中微小细节特征，而形态梯度常用来在图像中进行边沿检测，而局部梯度在检测小波包分解信号突变点方面也得到了一定应用［5-7］。本文将改进冗余第2 代小波包分解与局部梯度方法结合，并提出一种局部梯度谱熵指标，对试验滚动轴承进行故障诊断，能进行较好分类。

1 改进冗余第2 代小波包分解

如图1 所示其第1 层分解过程，原信号为x 经过1 层分解，获得逼近信号s⌒(1)与细节信号d⌒(1)，标准化系数分别为a1和b1。改进冗余第2 代小波分解得到的逼近信号c(1)与细节信号r(1)。用代替原信号得到下一层标准化系数，依此获得不同分解层数下的标准化系数。

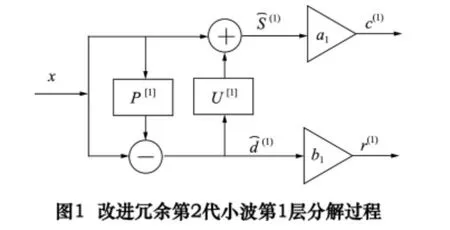
改进冗余第2 代小波包分解结果总能量与原始信号能量完全相等。因此，通过标准化系数消除了冗余第2 代小波变换的误差传播［6］。

2 基于改进冗余第2 代小波的滚动轴承振动信号的分解

2.1 滚动轴承振动信号的采集

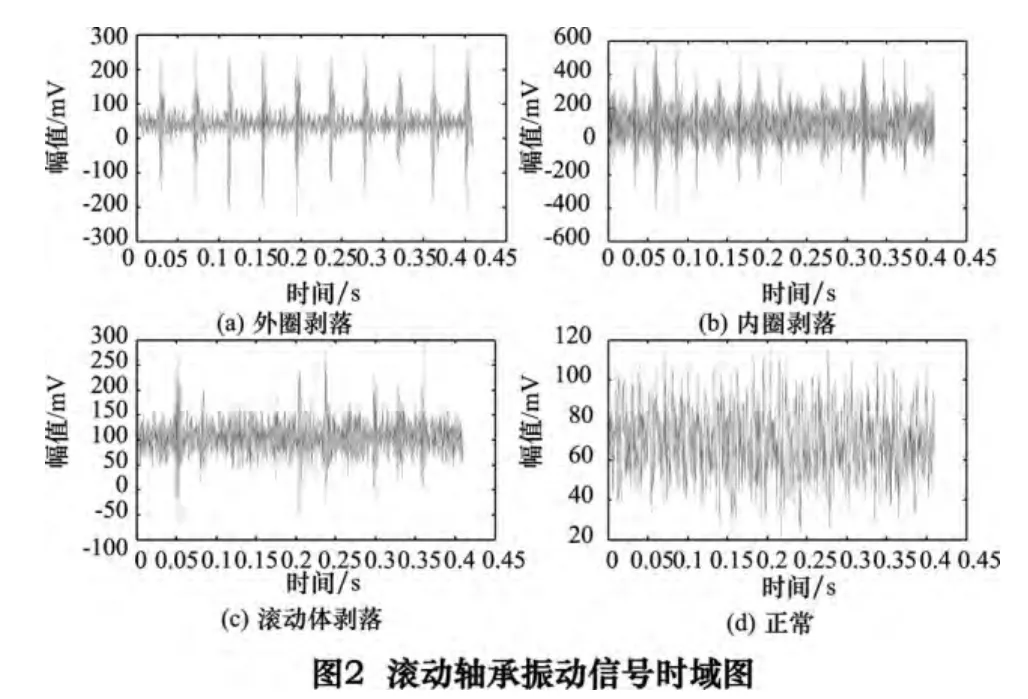
由实验台采集的6308 轴承振动信号，其采样频率20 kHz。轴承故障类型为:外圈剥落、内圈剥落、滚动体剥落和正常［7］。在4 种转速、3 种载荷下运转对轴承进行采样，如表1 所示不同转速的轴承故障特征频率。图2 为转速n1、轻载下的时域图。

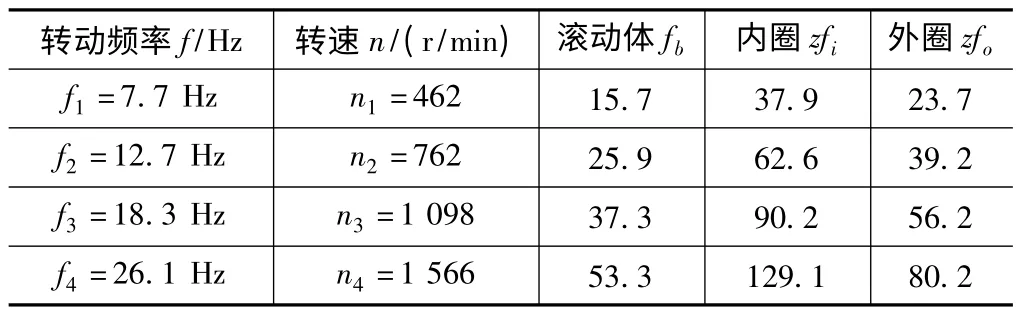
表1 滚动轴承的故障特征频率(Hz)

2.2 改进冗余第2 代小波的滚动轴承信号分解

如图3 所示，对图2a 信号进行冗余第2 代小波3层分解，得到8 频带载波，其第2～4 频带的与原信号的幅值较接近，其中4 频带最接近为200 mV 左右，每隔0.04 s 有一次脉冲，其频率约等于特征频率23.7 Hz。

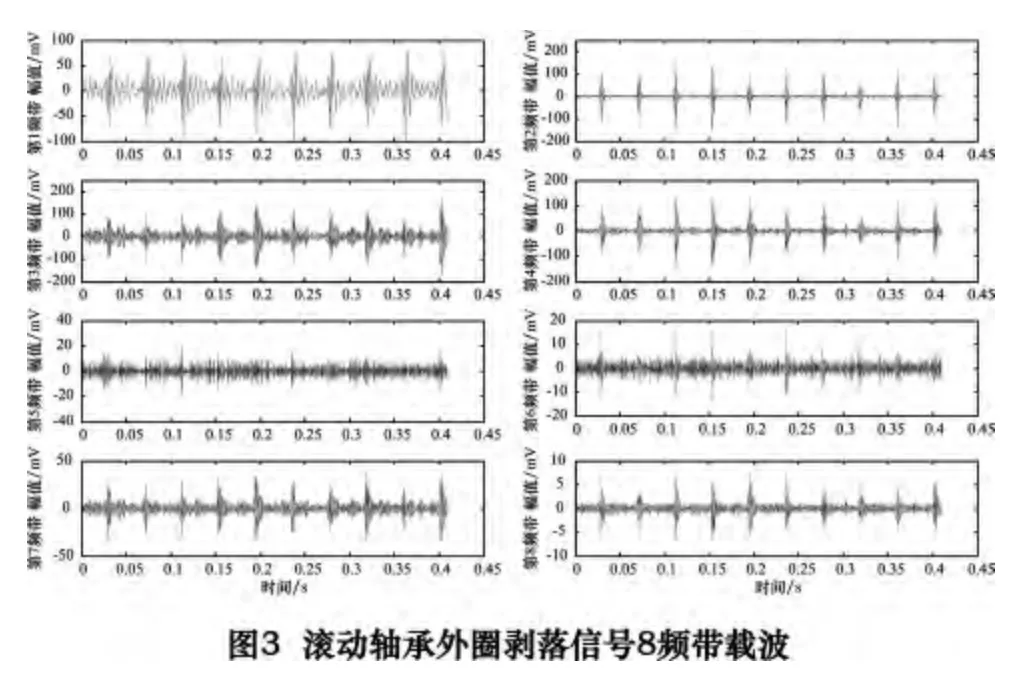
为比较不同频带载波和原信号的相关性，分别计算各载波和原信号的相关系数。

对图2 所示轴承信号的8 个频带载波信号与源信号计算其相关系数，如表2 所示。对于故障轴承，相关性最大的频带都在第4 频带，其值均大于0.75。而正常轴承最大频带都为第1 频带，其值大约为0.9，说明故障轴承第4 频带、正常信号第1 频带与源信号高度相似。对多组信号试验，结果同上。

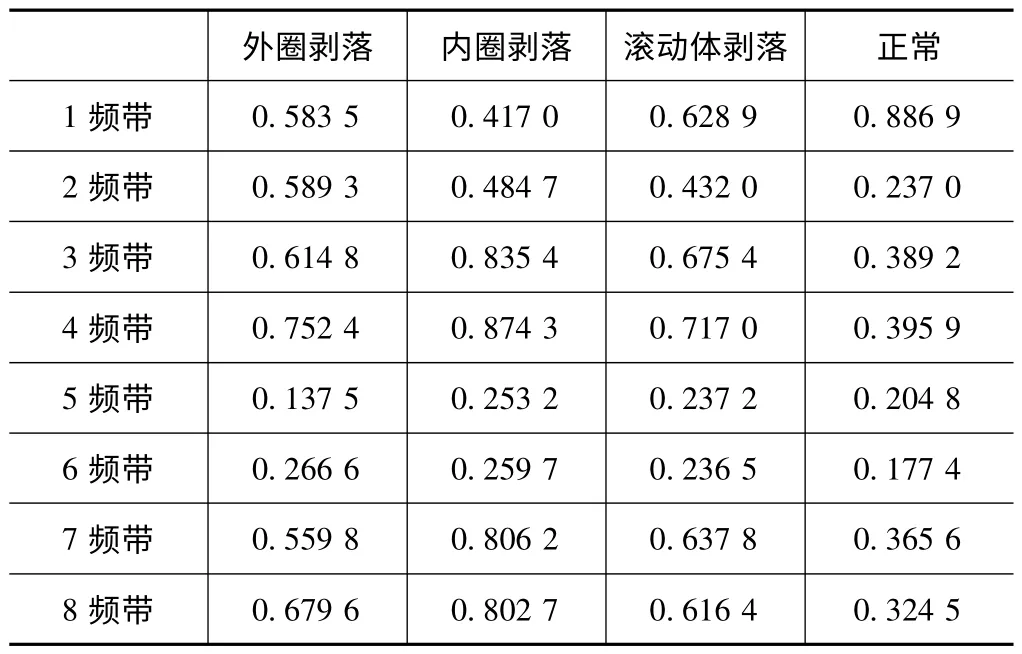
表2 滚动轴承8 频带互相关系数

3 滚动轴承载波信号局部梯度图

3.1 局部梯度图

设备运行状态的重要信息信号往往体现为不规则的突变点，局部梯度可较准确识别小波包分解后的突变点。

信号设为x={x(i)，i=1，2，…，n}，n 为数据长度，定义第i 点的局部梯度向量为

vi(j)=x(i)-x(i+j)，i=1，…，n，j=-r，…，r

可得到第i 个点相对于其相邻的第j 个点的变化，整个信号序列的局部梯度向量表示为

信号的局部梯度图定义为［6］

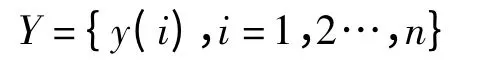
3.2 滚动轴承频带载波的局部梯度图分析

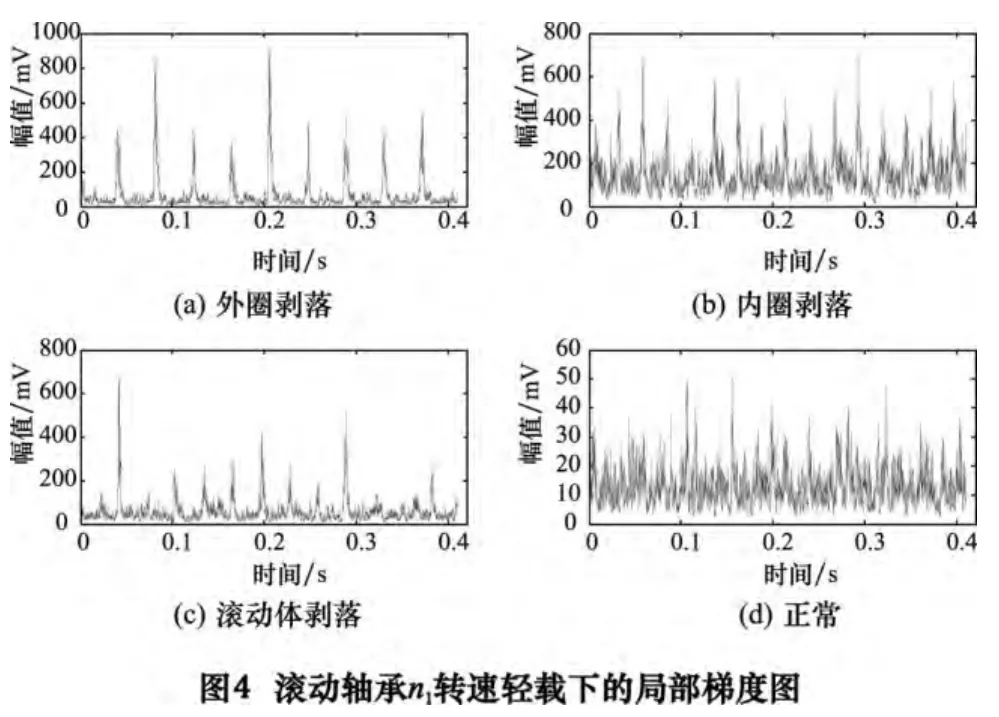
对图2 所示信号的最优载波求局部梯度，得到图4a～4c 所示故障轴承都可以看到存在周期性的脉冲，其中图4a 约隔0.04 s 有1 次脉冲，其频率正好接近于其特征频率23.7 Hz，而且最高的两脉冲间时间间隔约为0.125 s，其频率接近于转速1 转频7.7 Hz;图4b约0.025 s 有1 次脉冲，频率接近于特征频率37.9 Hz;图4c 约0.033 s 有1 次脉冲，其频率约其特征频率双倍频31.4 Hz;如图4d 所示，正常轴承的局部梯度图无周期性的脉冲。

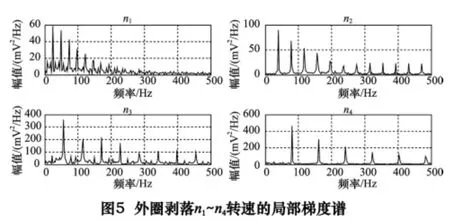
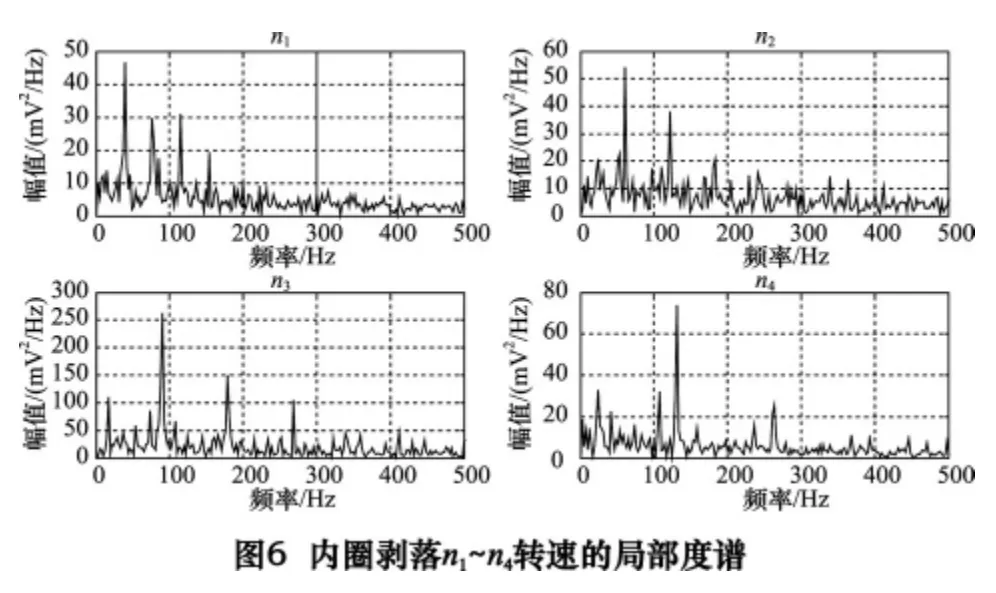
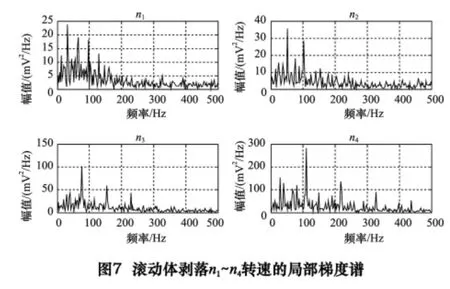
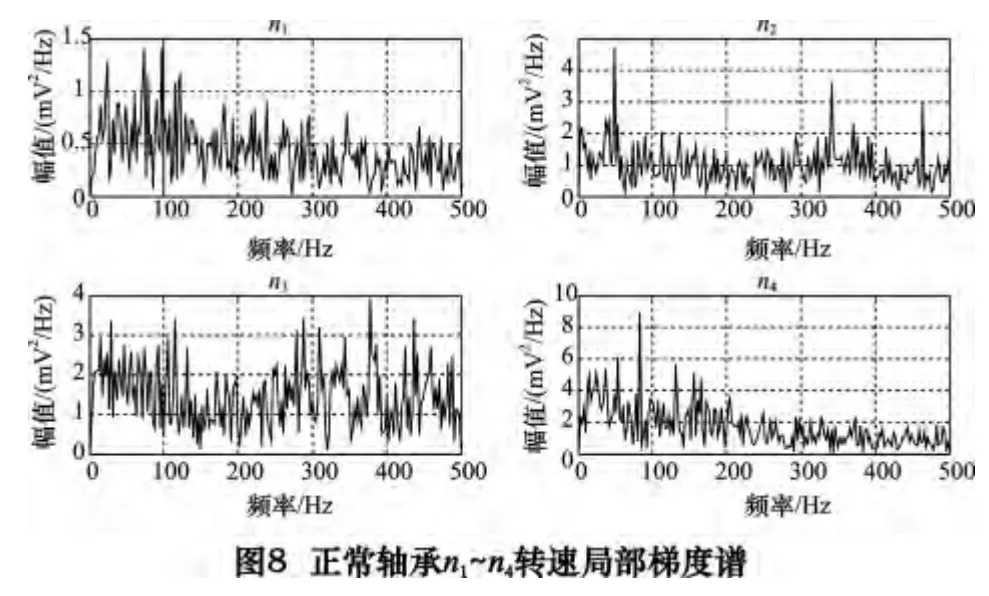
为比较不同转速下故障特征的提取效果，对轻载下n1～n4下不同转速的局部梯度求功率谱，得到图5～8。如图5 所示，在n1～n4的局部梯度谱上，分别在图示24、39、56、80 Hz 及其倍频处脉冲，接近于外圈剥落的特征频率及倍频;同样，如图6 所示，在39、61、90、131 Hz 及其倍频处脉冲，接近于内圈剥落的特征频率及倍频;同样，如图7 所示，在31、51、75、109 Hz及其倍频处脉冲，接近于滚动体剥落的特征频率双倍频;图8 中正常轴承局部梯度功率谱高频段没有脉冲，其4 种转速下的局部梯度谱脉冲呈随机分布状，有些突出的脉冲有可能是转频的倍频。综上所述，采用改进冗余第2 代小波包分解的局部梯度谱可以提取不同转速下的故障特征频率，正常轴承无缺陷，其局部梯度谱呈随机分布。

4 基于局部梯度谱熵的滚动轴承故障分类

从以上分析可以看到，最优载波局部梯度能够提取滚动轴承的故障信息的，可以此作为特征指标对信号进行分类。

利用局部梯度功率谱的冲击脉冲可识别故障特征，而信息熵可用来衡量信号不确定性，熵值越小，信息越确定;反之，越大，信息越不确定［8-10］。

如图9 所示，取不同转速下无载、轻载、重载下的共48 组试验轴承载波信号，求其局部梯度信息熵，结果为:正常轴承的局部梯度熵总大于故障轴承，原因是正常轴承信号往往呈随机分布，不确定性大;但是不同故障类型的轴承之间无法用该指标区分。

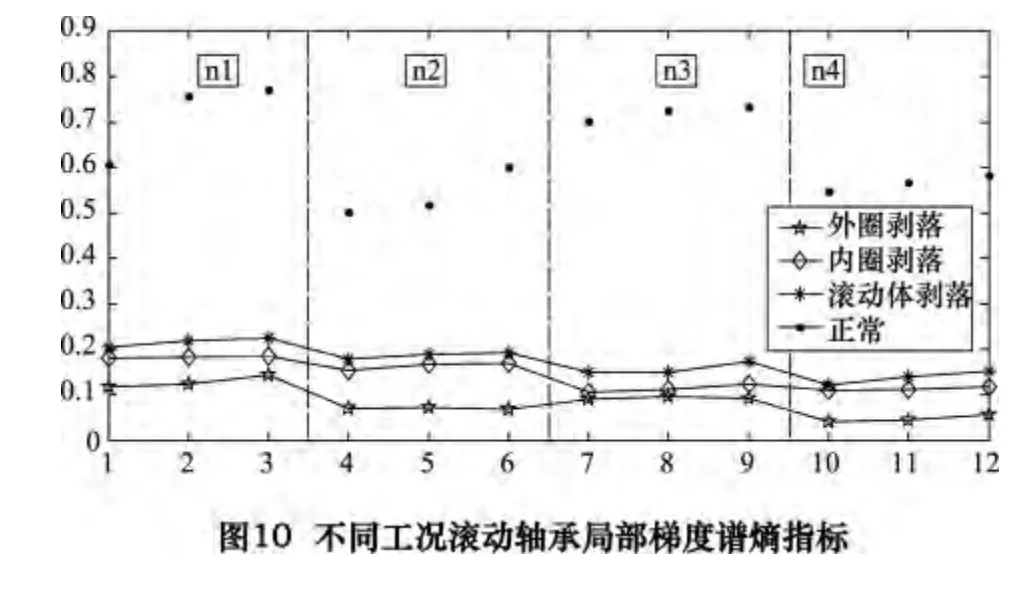
如图10 所示，对其局部梯度谱幅值求熵值，正常轴承远远大于故障轴承，而故障轴承的熵值大小顺序为:滚动体剥落＞内圈剥落＞外圈剥落

由图5～7 所示，分解后的载波信号局部梯度谱呈周期性波动，且外圈剥落的轴承周期性脉冲最明显，其信号越确定，熵值越小;内圈剥落和滚动体剥落其次，故其熵值稍小。而图8 所示正常轴承信号局部梯度谱呈随机波动，信号不确定，故其熵值最大;且从图9、10中可以看到，n1～n4四种转速下不同载荷下波形，图9所示的局部梯度熵随载荷和转速增加，熵值稍有增加;而图10 所示局部梯度谱熵随载荷变动不大。比较这两种指标，局部梯度谱熵指标比局部梯度熵的试验，轴承故障分类的效果要好。

5 结语

对试验轴承信号用改进冗余第2 代小波分解，得8 频带载波。根据互相关系数最大原则获得最优载波。求其局部梯度及功率谱，可从故障轴承局部梯度图中获得其特征频率所对应的周期性脉冲，其局部梯度谱可以获得不同故障特征频率及其谐波，而正常轴承波形随机分布。同时，提出基于载波信号的局部梯度谱熵指标，可以将试验工况的轴承信号区分开。

［1］丁建明，林建辉，杨强，等.基于谐波小波奇异熵的轴承故障实时诊断［J］.中国机械工程，2010，21(1):55 -58.

［2］史斐娜，刘广璞.基于冗余第二代小波变换的齿轮箱故障诊断［J］.煤矿机械，2014，35(5):248 -250.

［3］高立新，汤文亮，青永刚，等.基于冗余第二代小波的降噪技术［J］.北京工业大学学报，2008(12):1233 -1237.

［4］罗荣，田福庆，冯昌林，等.改进的冗余第二代小波包及其故障诊断应用［J］.华中科技大学学报自然科学版，2014，42(5):40 -46.

［5］李兵，张培林，任国全，等.基于形态梯度算子的滚动轴承故障特征提取［J］.中北大学学报:自然科学版，2011，32(4):426 -430.

［6］何正佳，袁静，訾艳阳，等.机械故障诊断的内积变换原理与应用［M］.北京:科学出版社，2012:112 -128.

［7］陈超，江涛，徐文学.基于平均梯度的多聚焦图像融合方法研究［J］.山东建筑大学学报，2009，24(2):133 -136.

［8］朱瑜，王殿，王海洋.基于EMD 和信息熵的滚动轴承故障诊断［J］.轴承，2012(6):50 -53.

［9］刘韬，陈进，董广明.基于频带熵的滚动轴承故障诊断研究［J］.振动与冲击，2014，33(1):132 -135.

［10］刘涛，黄成东.基于信息熵的涡旋压缩机故障诊断研究［J］.压缩机技术，2012，231(1):1 -8.