基于混沌理论的直流供电系统接地故障检测的研究

张霄

(三峡大学 电气与新能源学院，湖北 宜昌 443002)



基于混沌理论的直流供电系统接地故障检测的研究

张霄

(三峡大学 电气与新能源学院，湖北 宜昌 443002)

由于现有的直流供电系统接地故障检测有一定的缺陷，通过混沌动力学分析故障检测的两种方法结合对直流供电系统接地故障进行研究，即系统固有的混沌特性和加入混沌振子子检测系统，仿真结果表明，此新方法有较好的准确性。

混沌;直流供电系统接地故障检测;关联维数;duffing振子

1 引言

直流系统是发电厂和变电站主要工作电源，它为厂站的电气控制、中央信号、继电保护、自动装置及事故照明等提供可靠稳定的不间断电源。发电厂、变电站直流系统接地是一种常见的故障，可能引起继电保护误动或拒动。目前,国内外对于直流供电系统接地故障检测主要采用低频信号注入法。但该法和其他传统直流系统一点接地故障直流供电系统接地故障种类繁多、情况复杂,按检测法都存在固有的缺陷[1]。系统中存在的谐接地性质可分为绝缘降低和直接接触;按接地点数波、白噪声以及故障情况下产生的高频暂态分量等干扰信号都会影响检测结果[2]。直流供电系统中的浮充电整流器、大电容接地和环网等因素还会加剧干扰信号,使接地故障检测难以准确完成,甚至发生误判[3]。很多学者也试图把小波变换和智能控制方法引入接地故障检测,以期减少干扰信号对检测结果的影响。上述方法的共同思路就是将各种干扰信号作为系统噪声来处理。直流供电系统作为一种非线性动态系统,存在着混沌现象。故实际系统的干扰信号中既存在随机信号也存在混沌信号。如果将干扰信号作为噪声,采用滤波方法或用傅立叶变换提取状态特征值,都只能对随机干扰信号起作用。本文通过运用混沌动力学分析，开拓了一种新的思路。

2 直流供电系统

2.1 直接系统一点故障接地

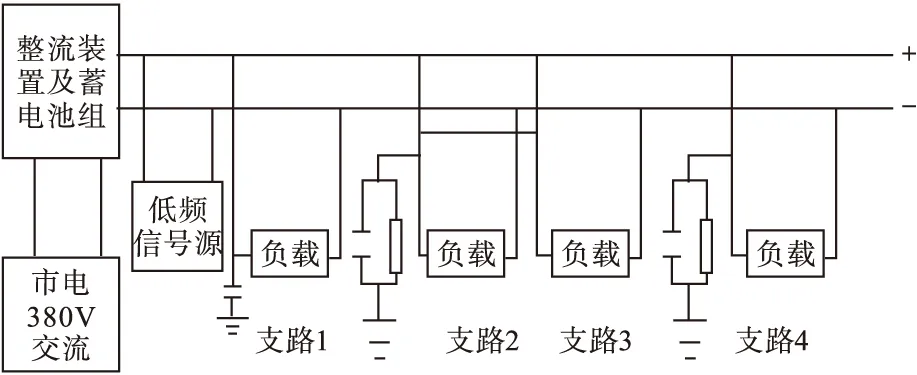
图1 直流供电系统

直流供电系统 发电厂及变电站的直流系统电源均采用110V或220V,正负母线对地浮空,所以系统一点接地故障时无短路电流流过,不致影响系统正常工作。但这种故障必须及早发现,以免另一点接地时可能引起信号回路、控制回路、继电保护回路和自动装置回路的不正确动作。规程中也明确规定了一点接地的允许时间(一般为60min)。

2.2 低频注入法以及其缺陷

直流系统发生一点接地故障后,向直流电网母线注入一个低频率的电压信号,用TA检测第一支路中产生的低频电流信号,在理想情况下只有发生接地故障的支路中才可检测到低频电流信号,其他支路上的TA输出为零。但低频信号法的检测结果常受到对地分布电容、环网谐波环流等的影响,另外,由于干扰信号的存在,正常支路的TA通常也会存在输出信号。一般的检测装置难以分辨干扰信号和电阻信号,进而导致误选。

3 混沌理论

3.1 混沌理论简介

混沌理论是一种用于描述确定非线性系统内在随机性的一种数学方法。作为确定论和概率论的桥梁,混沌理论具有对初始条件敏感、短期可预测等特点,近年来在各工程领域得到应用[5]。基于混沌理论的故障检测是一个新的方向。随着对混沌理论研究的逐渐深入,近年来混沌方法在工程技术的许多领域开始得到应用,并取得了丰硕的成果其中包括：心率测试分析、保密通信、电力电网动态分析和保护、流体混合、决策预测、机械振动故障诊断、计算机图形处理、控制系统优化等。相对于其他方面,混沌方法在动态系统故障检测中的研究起步较晚。1997年,俄国学者发表了第一篇将混沌理论用于故障检测的文章。最近几年的研究显示出混沌理论在动态系统故障检测领域的广阔应用前景。其主要研究方向可概括为:基于混沌时间序列预测的故障检测、基于混沌抑制的故障检测、基于混沌动力学分析的故障检测和基于关联维分析的故障检测等四个方面。对混沌系统进行定量分析的指标主要有分形维数、Lyapunov指数、Kolmoglov熵和Hurst指数等。

3.2 分形维数

分形与动力系统的混沌理论交叉结合，相辅相成。它承认世界的局部可能在一定条件下或过程中，在某一方面(形态，结构，信息，功能，时间，能量等)表现出与整体的相似性，它承认空间维数的变化既可以是离散的也可以是连续的，进而拓展了视野。

分形几何的概念是美籍法国数学家曼德布罗特(B.B.Mandelbrot)1975年首先提出的，但最早的工作可追溯到1875年，德国数学家维尔斯特拉斯(K.Weierestrass)构造了处处连续但处处不可微的函数，集合论创始人康托(G.Cantor，德国数学家)构造了有许多奇异性质的三分康托集。1890年，意大利数学家皮亚诺(G.Peano)构造了填充空间的曲线。1904年，瑞典数学家科赫(H.von Koch)设计出类似雪花和岛屿边缘的一类曲线。1915年，波兰数学家谢尔宾斯基(W.Sierpinski)设计了象地毯和海绵一样的几何图形。这些都是为解决分析与拓朴学中的问题而提出的反例，但它们正是分形几何思想的源泉。1910年，德国数学家豪斯道夫(F.Hausdorff)开始了奇异集合性质与量的研究，提出分数维概念。1928年布利干(G.Bouligand)将闵可夫斯基容度应用于非整数维，由此能将螺线作很好的分类。1932年庞特里亚金(L.S.Pontryagin)等引入盒维数。1934年，贝塞考维(A.S.Besicovitch)更深刻地提示了豪斯道夫测度的性质和奇异集的分数维，他在豪斯道夫测度及其几何的研究领域中作出了主要贡献，从而产生了豪斯道夫-贝塞考维奇维数概念。

分形几何学是一门以非规则几何形态为研究对象的几何学。由于不规则现象在自然界是普遍存在的,因此分形几何又称为描述大自然的几何学。但目前分形还没有一个确切的定义,分形是对没有特征长度但有某种意义下的自相似性的形体和结构的总称。分形维数是描述分形的重要参数，能够反映分形的基本特征，但由于侧重面不同，有多种定义和计算方法。主要有：相似维数，容量维数，信息维数，记盒维数，关联维数。其中关联维数已经比较多的用于了非线性动态系统的故障检测中[6]。

3.3 Duffing振子

Duffing振子是目前研究较为充分的、典型的混沌系统模型之一。Duffing振子信号检测技术利用混沌系统的分岔特性来检测外界信号,将待测信号作为Duffing方程周期策动力的摄动,噪声即使强烈,对系统的状态也不会造成影响,而一旦有特定的信号出现,即使幅值较小,也会使系统发生相变。利用Duffing振子系统的这种初值敏感性可以获得很高的测量灵敏度和良好的抗噪性能。

4 混沌理论在故障检测中的应用

本文提出一种将混沌理论用于直流供电系统接地故障检测的方法,其主要思想为：

(1)采集支路电流信号，通过相空间重构求取其关联维数。

(2)建立一个Duffing 振子的子检测系统，支路电流信号作为摄动力给予观察系统相轨迹图的变化。

通过两者相结合进行判断。

4.1 Simulink仿真

本文采用频率10Hz,幅值为2V的交流信号作为低频信号源，在Simulink中搭建直流系统含环网接线的10个支路的直流仿真模型。

图2 直流供电系统 Simulink仿真模型

4.2 关联维数的求取

(1)关联维数的定义

关联积分：

(1)

它是相空间中针对每个向量在半径为r的超球内的相邻量数，r为重构相空间的超球半径，H(r)为单位阶跃函数。

(2)

(2)具体算法

从一维数据序列计算关联维数方法是采用由P.G和I.G在嵌入定理和重构相空间理论基础上提出的g-p算法。在一维数据序列：x1，x2，……，截取前m个数据，构成m维相空间的一个向量x1，然后一次向后移t个数据，构成m维空间的另一个向量，t为构成相空间的采样间隔，采用右移动发得到一维时间序列的一个展拓m维相空间的点集。

任选m维相空间点集中一个参考点计算除它外所有的其他点的距离，以小标量r为半径的体积元中的点的个数，从而得到关联积分。

(3)

其中H(r)为单位阶跃函数；

(4)

(3)算法中关键值的选取

领域半径r：以r～[min||Xi-Xj||，max||Xi-Xj]范围进行区间选取；步长：采用均匀递增，保证平缓变化；延时时间：采用自相关函数法，即对于一个时间序列x(t),先写出其自相关函数，当下降到初始值1-1/e时，所得时间t就是重构空间的延时时间；嵌入维数m：采用的是试凑法，即m逐步增加，当关联维数随m增加不改变时，m即为所得；无标度区间：Inc(m，r)～Inr关系曲线上的线性部分；一般需要主观判定，主观的选取区间，然后判定该区间线段的斜率是否达到饱和。本文通过基于BDS统计限定范围的快速自动判定法，根据BDS统计结论，可以选定[In(σ/2)，In(2σ)](时间序列的均方差)为无标度区间界限；

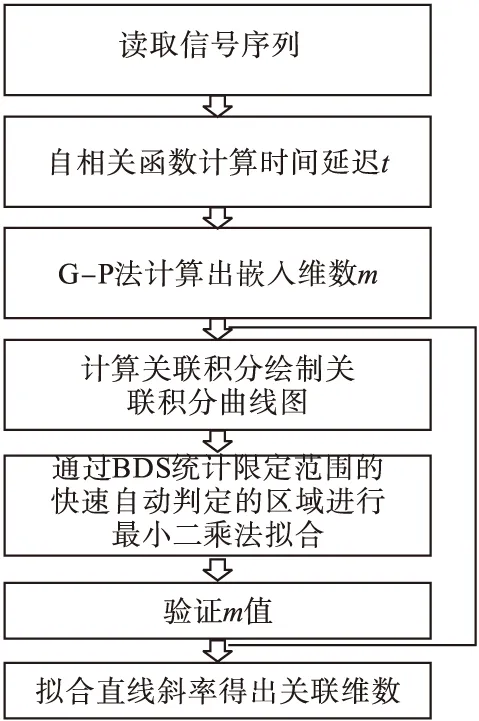
图3 关联维数算法流程图

4.3 duffing振子的子检测系统

Duffing振子混沌系统拥有很好的抗噪性，对于特定微弱信号有很大的敏感性。

完整的duffing振子方程：

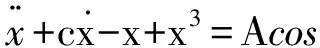
(5)

C为阻尼比，-x+x3为恢复力项,Acos(t)为内置周期策动力。以上方程是w=1，为了实现不同的频率信号的检测，设t=wτ则原方程改写为：

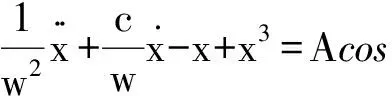
(6)

图4 duffing振子模型

由于接地故障导致系统发生结构改变，信号随之发生改变，把待测信号通过电流互感器采集，在作为摄动力给予duffing振子子检测系统观察相轨迹变化，从而判断是否接地。

5 仿真结果

5.1 关联维数

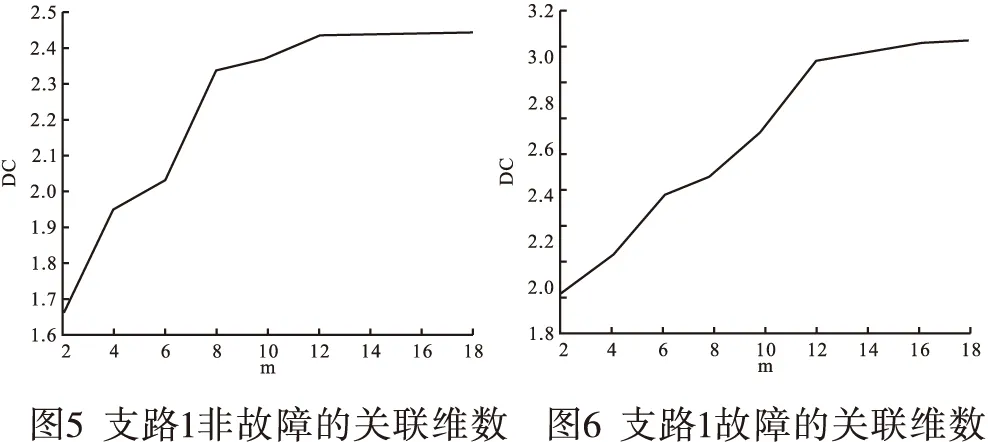
通过对比，显然，在接地与非接地两种情况下，支路采集信号的关联维数明显不同。接地情况下关联维数明显高于非接地情况。无接地故障饱和关联维数为2.41，接地故障饱和关联维数为3.13。

5.2 相轨迹图

非故障下支路电流信号作为摄动力给予duffing振子子检测系统得到的相轨迹图。

故障下支路电流信号作为摄动力给予duffing振子子检测系统得到的相轨迹图。

图7

图8

6 结论

本文用混沌理论分析直流供电系统的接地故障检测，其优点有：

(1)无需要改变系统结构，直接采集电流互感器的信号进行分析；

(2)该方法的思想有利于使用微机保护装置进行分析；

(3)关联维数在接地与非接地的情况下有明显的不同，接地下的关联维数明显偏大，可以通过计算正常情况下的关联维数作为基准值来作为判别依据；同时，通过相轨迹图的比较，接地与非接地情况下的相轨迹图差异很大，通过关联维数和相轨迹图相结合来判别系统。

本文作为一项创新性的研究，无论是算法还是思想都有利于直流供电系统接地故障在线检测的研究，通过仿真验证了其可行性。

[1] 程跃森.直流系统接地检测装置的研究[D].河北：华北电力大学,2007.

[2] 田伟达.直流系统接地故障检测方法的研究[J].东北电力大学学报,2011(1).

[3] 朱秀香.基于直流注入原理的配电网单相故障选线定位研究[D].济南大学,2011.

[4] 齐超.基于信号注入的小电流接地系统离线故障定位研究[D].北京：华北电力大学,2009.

[5] 李娜,方彦军.利用关联维数分析机械系统故障信号[J].振动与冲击,2007(4).

[6] 汪慰军,陈进,吴昭同.关联维数在大型旋转机械故障诊断中的应用[J].振动工程学报,2000(2).

Research on Earth Fault Detection of DC Power Supply System Based on Chaotic Theory

ZHANGXiao

(College of Electrical and New Energy Source,Sanxia University,Yichang 443002,China)

The DC power supply system of the existing grounding fault detection has some shortcomings,two kinds of methods for fault detection through the chaotic dynamics analysis of a comprehensive study of the grounding fault in DC power supply system,namely chaotic characteristics of the system inherent and join the chaotic oscillator sub detection system,the results show that compared with the existing detection systems have a certain to improve.

chaoticaos theory；grounding fault detection of DC power supply system；the correlation dimension；duffing oscillator

1004-289X(2015)04-0050-05

TM71

B

2014-12-29