霍尔推力器工作性能数值模拟研究

龙建飞，张天平，孙明明，高 俊，贾连军

(兰州物理研究所 真空低温技术与物理重点试验室，兰州 730000)



霍尔推力器工作性能数值模拟研究

龙建飞，张天平，孙明明，高 俊，贾连军

(兰州物理研究所 真空低温技术与物理重点试验室，兰州 730000)

为了模拟霍尔推力器推力、比冲等工作性能，采用粒子网格单元与蒙特卡洛相结合(PIC/MCC)方法，建立了霍尔推力器二维轴对称模型。模型中电子和离子均采用粒子描述，中性原子为背景气体，自洽电势通过求解泊松方程获得。跟踪推力器出口处离开的离子数量、轴向速度等信息，通过统计计算得到推力器的推力、比冲。以LHT100推力器为研究对象，针对不同的工作参数(阳极流量在4.6～5.4 mg/s，阳极电压在280～320 V之间)共进行了9种工况数值模拟，并进行试验对比验证，模拟结果与试验测试结果均较好吻合，最大误差小于10%。

霍尔推力器；工作性能；蒙特卡洛；粒子单元法；数值仿真

0 引言

霍尔推力器具有高可靠、高功推比等特点，作为空间动力装置而广泛应用于卫星的位置保持和姿态控制等空间任务中[1-2]。推力和比冲作为霍尔推力器的主要性能而备受关注，是衡量该推力器能否空间应用的重要指标。对霍尔推力器的推力和比冲等性能进行仿真研究，可明晰该推力器工作物理过程，以及为性能优化提供理论支撑，具有重要意义。

霍尔推力器的推力及比冲等工作性能的理论计算主要是通过经验模型[3-4]获得，建立的经验模型一般是推力器工作参数和结构参数的函数。在经验模型建立过程中，涉及电势分布、等离子体密度、工质利用率等相关敏感参数，而这些敏感参数很难通过试验精确测出。因此，均是通过经验估值给定，这便使得经验模型存在一定偏差。同时，推力器在不同工况下，敏感参数的不一致性，甚至会随工作参数存在较大变化，这便加大了经验模型误差，进而使得模型不能满足广泛工作条件。关于霍尔推力器放电室数值模拟研究已经开展了大量研究，Szabo[5]建立了放电室的全粒子模型，Fife[6]和Hofer等[7]建立了混合模型等，均对霍尔推力器放电室工作过程进行了数值模拟研究，得到了放电室内电势分布、等离子体密度和能量分布等重要信息。国内刘辉等[8]采用PIC/MCC方法，对霍尔推力器放电室内电子运动行为进行了数值模拟研究。而关于霍尔推力器工作性能的数值仿真，特别是广泛工作条件下的仿真计算，目前还鲜有文章报道。

本文将采用全粒子PIC/MCC方法，建立霍尔推力器放电室二维轴对称模型，对放电室等离子体进行仿真，跟踪推力器出口处离开的离子信息(主要是离子数量和轴向速度)，通过建立的性能模型计算，进而模拟出霍尔推力器的推力和比冲性能，针对广泛的工作参数(阳极流量在4.6～5.4 mg/s，阳极电压在280～320 V之间)共进行了多工况数值模拟，并开展试验验证研究。

1 数值模型建立

1.1 模拟区域及网格划分

霍尔推力器具有轴对称的几何结构，且推力器的参数在周向的变化相对较小。因此，可采用2维柱坐标进行模拟，具体包括轴向(z)和径向(r)的二维空间和3维速度(Vz，Vr，Vθ)，θ表示轴向方向。图1为所选取的计算区域，计算区域主要为推力器放电室加速通道，左侧边界为推力器阳极。根据LHT100推力器尺寸，加速通道长度取26 mm，内壁面位于r=35 mm位置处，外壁面位于r=50 mm位置处。采用正交等距划分网格，长度为0.5 mm。因此，通道网格划分为52×30的等距网格。

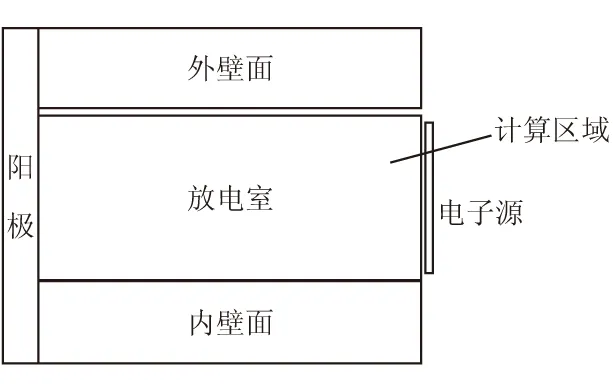
图1 计算区域选取示意图Fig.1 Schematic of calculation area

1.2 电磁场及粒子运动

在采用PIC粒子模拟方法建模时，均采用静电模型。因此，电场采用泊松方程求解[9]。

(1)

式中Φ为电势；ε0为真空介电常数；ni为离子密度；ne为电子密度。

泊松方程求解采用有限差分法，所使用的格式为中心差分五点格式。为了提高电场计算收敛的速度，文中采用逐次超松弛(SOR)方法。

采用三维磁场测试仪，对LHT100推力器的真实工况磁场进行测试，并将结果进行导入。磁场在整个计算过程一直保持不变。由于在霍尔推力器中，带电粒子自身产生的磁场较小，对计算结果影响不大。因此，为了简化计算，忽略带电粒子自身产生的磁场，即只考虑线圈产生的磁场。

霍尔推力器的阴极位于推力器外部，模拟真实的阴极需要较大计算量，并增加了程序设计的难度。因此，本文没有模拟真实的阴极，而是在推力器出口采用虚拟的阴极向通道内喷射电子。每个时间步长喷射进入通道的电子数量为

(2)

式中Id为放电电流；Δt为时间步长；w为仿真粒子的权重；q为电子电荷；Δnc为上一个时间步长从推力器出口处离开的粒子数。

入射电子满足半麦克斯韦分布，其能量为15 eV(与阴极触持极电压保持一致)。

由于原子的速度远小于离子和电子，因此在模型中，认为原子的分布是背景场。原子数密度分布近似地可表示为

(3)

式中na为原子密度；m为阳极流量；s为推力器出口端面积；v0为原子速度，原子速度在放电室内处处相等。

在模型中，模拟粒子的加速采用牛顿-洛伦兹力求解[10]

(4)

模型中认为粒子之间只有电子一原子碰撞才能生成离子，进一步认为只产生单电荷离子。电子和原子的碰撞概率表示为[11]

p=1-exp(-naveσtΔt)

(5)

式中ve为电子速度；σt为电子与原子间的碰撞截面，其值与电子能量有关。

由于在每个时间步长里都要计算所有电子的动能及碰撞概率，计算量很大。因此，本文采取Birdsall和Vahedi提出的空碰撞的方法[12]。

1.3 模拟计算简化

在目前的计算机硬件条件下，使用普通计算机直接模拟离子与电子的运动是非常困难的，因为离子比电子重，其质量比电子质量高3个数量级，这将导致离子的收敛很慢，计算时间过长。为了能够同时模拟电子和离子的运动，引入人工质量比[8]，将离子的质量人为的减小2 500倍数，以达到加速收敛的作用。此外，采用增大介电常数[8]1 600倍减少网格数量，进一步减小计算收敛时间。

1.4 工作性能模型

霍尔推力器是通过电能转化将工质气体(氙气)电离，并通过自洽电场将离子加速喷出，进而产生推力。这一过程可采用动量守恒方程进行描述，推力产生示意图见图2。图2中，Δv、m分别为推力器在Δt时间后推力器所获得的速度增量和喷出的粒子质量；u为喷出粒子所获得的平均轴向速度(相对于推力器)。

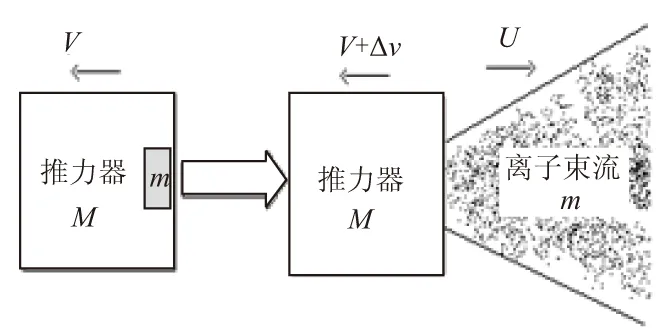
图2 霍尔推力器推力产生示意图Fig.2 Schematic diagram of thrust form in Hall thruster

假设推力器受到的外力的合力为∑F，根据动量定理，该过程满足方程：

(M-m)(v+Δv)+m(v-u)-Mv=(∑F)Δt

(6)

对式(6)做进一步分析：(1)忽略上式中mΔv高阶项；(2)推力器在空间工作过程中，只受到喷出束流反作用力的作用，即外力为零；(3)推力器出口喷出的粒子主要考虑离子。由于电子质量远小于离子，同时原子不受电场加速(速度过小)。因此，推力主要由喷出的离子产生。根据作用力与反作用力，则可得到推力器受到的推力，以及推力器获得的比冲。

(7)

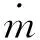
从式(7)中可得出，推力器获得的推力等于单位时间内喷出束流离子的总动量。而比冲为喷出离子的平均轴向速度。为了获得推力和比冲性能，通过稳态工况下的数值仿真，统计出口处离开离子的数量和轴向速度，由于单个离子质量已知(Xe+)，则可求出单位时间喷出的离子总动量，对应为霍尔推力器的推力。根据比冲定义公式，可进一步求出比冲。

2 放电室等离子体仿真

对额定工况(阳极流量：5.0 mg/s，阳极电压为300 V)下LHT100推力器工作过程进行了仿真，分别得到了放电室内的电势分布、等离子体密度分布和离子轴向速度分布等重要信息。

图3为推力器放电室内电势分布。仿真结果显示，电势沿径向具有较好的一致性，沿轴向电势降主要集中在放电室末端，离阳极约20 mm以后开始大幅下降，仿真结果与Fife等[6]研究结果基本一致。放电室内电势分布主要由电子的电导率分布决定的。为了保证有足够的电子到达阳极以维持放电的稳定性，近阳极区域的电导率相对需要较大。而在电离区，为了保证电子具有足够的能量向阳极迁移以维持放电，使得电离区电导率要根据电子温度的变化向阳极方向逐渐增大。在推力器出口末端很窄一段区域内，为了让离子获得较高的加速电压，同时要使电子从阴极穿越加速区到达电离区的过程中得以“升温”，确保电场提供给电子的能量足以弥补电子迁移过程中因碰撞而造成的损失，即该区域的电导率较小。因此，电导率的特征分布就决定了电势分布。

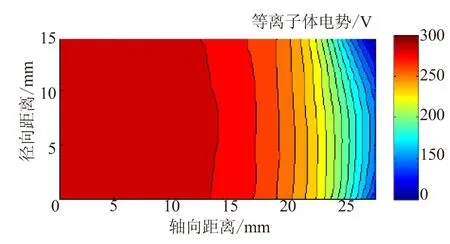
图3 等离子体电势分布Fig.3 Plasma potential distribution in discharge room

图4为放电室离子密度分布。仿真结果显示，通道内部最大离子数密度量级为1018mm-3，与Fife等[6]研究结果基本一致。离子密度分布与放电室内部的磁场分布是密切相关的。放电室径向磁场沿轴向呈“正梯度”磁场分布，即出口处的磁感应强最强，而阳极附近最小。磁场强度决定了放电室内对电子约束能力，也间接地决定了原子的电离区域。仿真结果显示，等离子体主要分布在中下游，对应于放电室的电离区，与放电室的特征区域[8]是相匹配的。

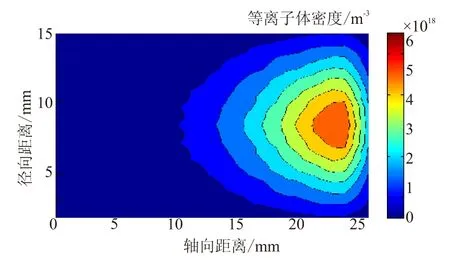
图4 放电室离子密度分布Fig.4 Pion density distribution in discharge room

图5为放电室内离子速度分布。从图5可看出，离子轴向速度沿轴向逐渐增大，在出口处有最大轴向速度，约16 000 m/s，与文献[6]基本一致。离子的轴向速度分布与放电室内加速电场强度分布有密切关系，而电场分布决定于放电室的电势分布。通过前面电势分布可看出，在近阳极区电势分布变化不大，因而电场强度很小。在电离区特别是加速区，电势降沿轴向明显增大，即加速电场增大，使得离子获得速度增量增大，即在出口处获得最大速度。

图5 放电室离子轴向速度分布Fig.5 Ion axial velocity distribution in discharge room

3 性能仿真及试验验证

3.1 仿真工况及测试方法

霍尔推力器的推力和比冲等性能主要受阳极流量和阳极电压等工作参数的影响。在空间应用中，面临复杂的工作环境，工作参数一般具有额定工作点±5%的振荡偏差。因此，为了系统验证该模型的准确性，验证条件尽量涵盖了空间应用中各种变化条件。同时考虑计算量，本文共选取9中工况进行推力、比冲进行仿真和试验验证研究，具体工况见表1。表1中，*表示额定工况。

霍尔推力器地面试验中，推力采用微小推力测试方法获得，比冲根据试验测试推力除以试验时流量得到。微小推力测试装置示意图及推力器测试工作情况见图6。

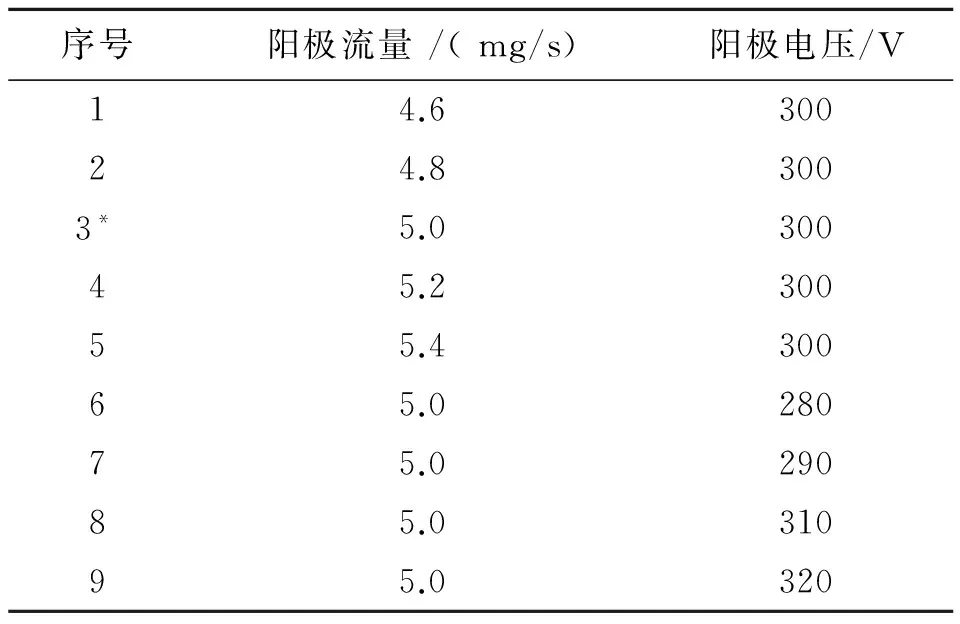
表1 工作参数选择Table1 The list of working parameter

3.2 推力验证

图7为推力性能的仿真与试验验证，其中共仿真了9种工况。从推力性能对比结果来看，仿真结果相比试验结果偏低，在第9种工况下有最大误差约9%(仿真结果为79.6 mN，测试值87.2 mN)。分析认为，主要存在3点原因：(1)仿真推力计算中，只是统计了离子，忽略了电子和原子的微推力效应，特别是原子经过放电室加热后具有一定的速度，从推力器出口流出也会产生一定的推力；(2)研究表明，出口到阴极之间仍存在电势差[13]，这部分电势差仍将对离子加速，对应仿真推力比实际测试值偏小；(3)推力测试试验中本身存在误差，特别是本地压强的存在(约1×10-3Pa)，会导致推力测试偏大，而仿真中并未考虑本底压强因素。

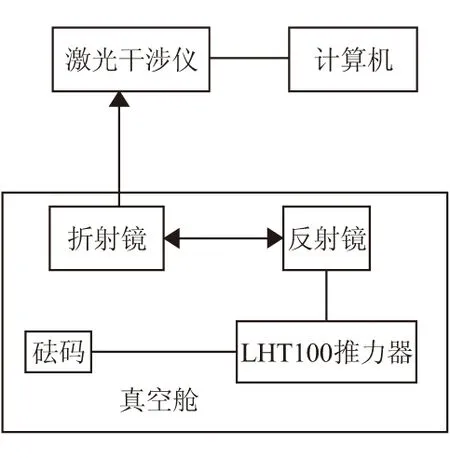
(a)推力测试装置

(b)推力测试过程

3.3 比冲验证

图8为比冲性能的仿真与试验验证，其中共仿真了9种工况。从比冲性能对比结果来看，在阳极流量变化情况下(前5种工况)，仿真结果比较平稳，而测试结果随阳极流量增大而较快增长，以致两者差异增大。而在阳极电压变化情况下，仿真结果与测试结果之间的差异较为稳定。其中工况5情况下，两者有最大误差约7.5%(仿真结果为1 587 s，测试结果为1 715 s)。分析认为，本模型中忽视了二价离子的存在，而这部分离子可获得较高速度，使得仿真出来的比冲比测试值偏低。同时，从出口到阴极之间仍占有一定的电势差，这其中有一部分电势降仍对出口后离子加速。所以，根据出口离子速度统计得到的比冲要比实际比冲偏小。

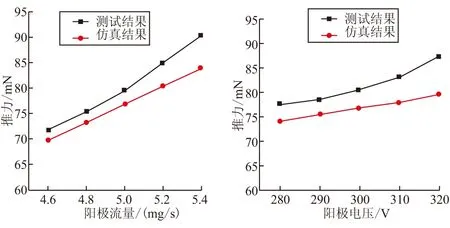
(a)推力随阳极流量变化关系 (b)推力随阳极电压变化关系

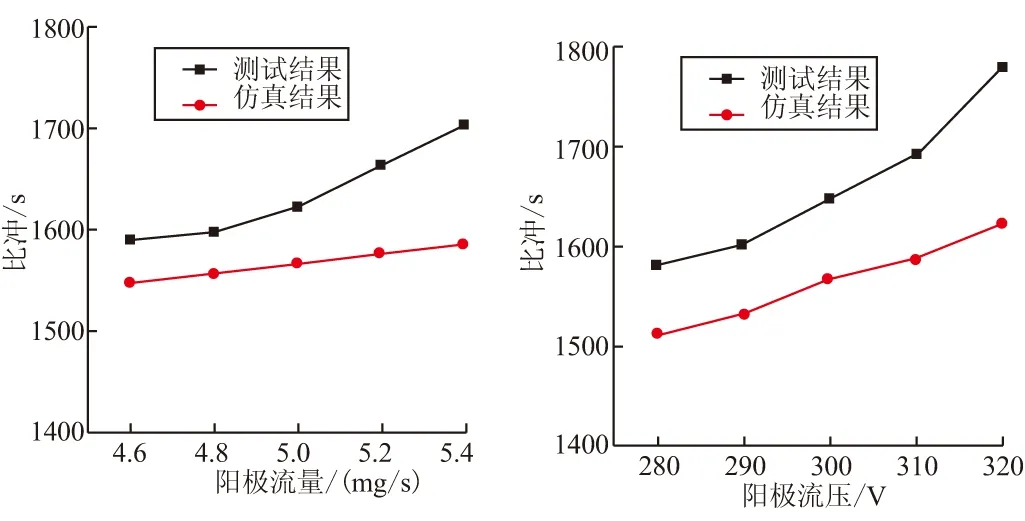
(a)比冲随阳极流量变化关系 (b)比冲随阳极电压变化关系

4 结论

(1)建立了霍尔推力器新的性能模型。模型中，推力、比冲是等离子体微观参数的相关函数。

(2)采用(PIC/MCC)数值模拟方法跟踪放电室内离子的运动轨迹，通过统计得到了离开离子的速度和数量等微观信息，进而得到了推力和比冲等性能。

(3)对放电室等离子体进行了数值仿真研究，得到了放电室电势分布、等离子体密度分布及离子轴向速度分布等信息，仿真结果与国外文献能较好吻合。

(4)在阳极流量4.6～5.4 mg/s、阳极电压280～320 V范围内，共仿真计算了9种工况下推力器推力、比冲性能。将仿真结果与试验测试值进行对比验证，推力最大误差9%，比冲最大误差7.5%。

[2] 张天平. 国外离子和霍尔电推进技术最新进展[J]. 真空与低温，2006, 12(4)：187-190.

[2] 赵杰，唐德礼，耿少飞. 圆柱形霍尔推力器内等离子体数值模拟[J]. 固体火箭技术，2010, 33(1)：54-58.

[3] Kim V. Main physical features and processes determining the performance of stationary plasma thrusters[J]. Journal of Propulsion and Power, 1998, 32(14)：5736-5743.

[4] Brophy J, Barnett J. Performance of the stationary plasma thruster: SPT-100[R]. AIAA 92-3155.

[5] Szabo J. Fully kinetic numerical modeling of a plasma thruster[D]. Massachusetts: Massachusetts Institute of Technology, 2001.

[6] Fife J. Hybrid-PIC modeling and electrostatic probe survey of hall thrusters[D]. Massachusetts: Massachusetts Institute of Technology, 1998.

[7] Hofer R R, Mikellides I G, Katz I．Wall sheath and electron mobility modeling in Hybrid-PIC Hall thrusters simulations[R]. AIAA 2007-5267.

[8] 刘辉. 霍尔推力器电子运动行为的数值模拟[D].哈尔滨: 哈尔滨工业大学，2009.

[9] 贺碧蛟，张建华，蔡国彪. 稳态等离子体推进器羽流场数值模拟[J]. 北京航空航天大学学报，2005, 31(9): 145-148.

[10] 孙安邦，毛根旺，陈茂林, 等. 霍尔效应推力器羽流的PIC/MCC模拟[J]. 固体火箭技术，2009, 32(6): 638-640.

[11] Garrigues L, Bareilles J, Boeuf J. Modeling of the plasma jet a stationary thruster[J]. Journal of Applied Physics, 2002, 91(12): 9521-9524.

[12] Birdsall C K，Langdon A B．Plasma physics via computer simulation[M]．New York：McGraw Hill Higher Education，1984.

[13] Yu D , Li Y, Song S. Ion sputtering erosion of channel wall corners in hall thrusters[J]. Journal of Physics D: Applied Physics, 2006, 39(4): 2205-2211.

(编辑：崔贤彬)

Numerical simulation of performance in Hall thruster

LONG Jian-fei, ZHANG Tian-ping, SUN Ming-ming, GAO Jun, JIA Lian-jun

(Science and Technology on Vacuum Cryogenics Technology and Physics Laboratory, Lanzhou Institute of Physics, Lanzhou 730000, China)

To simulate the thrust and specific impulse of a Hall thruster, a two-dimensional axisymmetric model is developed for the discharge channel of the thruster, the model is based on a particle description of electrons and ionic components, the neutral atoms are set as background, and the self-consistent electric potential is calculated from Poisson equation. In the process of tracking, the number and energy of ions ejecting from exit plane were recorded, then the thrust and specific impulse were obtained by statistical calculation. Treat LHT100 thruster as research object, according to different working parameters (anode flow rate is 4.6～5.4 mg/s, anode voltage is 280～320 V), numerical simulation were conducted in 9 kinds of conditions, respectively. By experiment validation, the simulation results and experiment results are consistent, the maximum error is no more than 10%.

Hall thruster；performance；Monte Carlo；particle-in-cell；numerical simulation

2014-08-25；

：2014-12-15。

真空低温技术与物理重点实验室基金(9140c550206130c5503)。

龙建飞(1984—)，男，博士，研究领域为空间电推进技术。E-mail:ljf510@163.com

V493

A

1006-2793(2015)04-0514-05

10.7673/j.issn.1006-2793.2015.04.012