基于灰色马尔科夫链模型的交通事故预测
艾克热木·艾合买提,阿肯江·托呼提,王立晓
(新疆大学 建筑工程学院,新疆 乌鲁木齐830047)
道路交通系统是一个基于人、车、路的动态系统,影响交通安全的因素很多,作用机理复杂,因此道路交通事故的发生具有很大的随机性和偶然性。交通事故根据传统的回归预测法、时间序列法、BP神经网络法进行预测时,由于各模型均存在一定的局限性,因此预测结果往往出现较大偏差。回归预测法具有回归系数较难确定,所需样本量较大等缺陷;时间序列法由于考虑的因素较少,不能反映随机的外部环境影响,预测结果的准确性、实用性较差;BP神经网络预测法则需要输入较为全面的数据,而且收敛速度慢,程序复杂。
1 灰色马尔科夫链GM(1,1)模型
1.1 灰色GM(1,1)模型
灰色GM(1,1)模型首先通过对原始数据进行累加,建立均值生成序列和矩阵B与Y,然后通过最小二乘回归和微分等数学方法建立模型,最后通过模型得到的值经过还原数据,得到预测结果。它的建模过程为
1)根据模型在各个时刻的值,建立如式(1)所示的原始数据序列
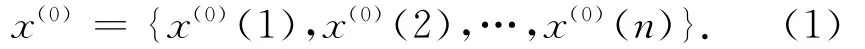
2)对原始数据序列进行累加(作1-AGO),得
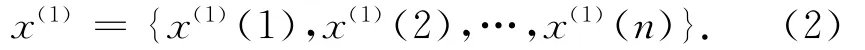
3)对1-AGO序列作均值,生成序列

4)利用式(1)与式(3),建立矩阵Y与B,得

5)对参数进行最小二乘估计,得出a与b的值
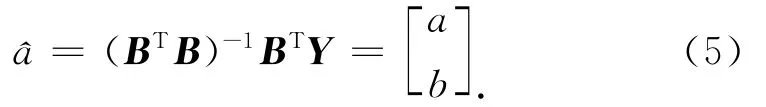
6)确定模型形式,并还原得到的灰色预测值,如式(6)、式(7)所示

1.2 马尔科夫链模型
马尔科夫链是根据所观察的离散状态,以经验为主的估计转移概率参数化的随机过程。它是对原始数据进行状态划分,求出转移概率矩阵,得出未来的预测值。以灰色马尔科夫链模型为例,其一般步骤如下:
1.2.1 状态划分
根据灰色模型预测值与实际值间的相对误差,把相对误差分成r类状态。状态划分数量并无严格规定,是综合考量样本数量、拟合的误差范围等相关因素而确定,一般分成3~5类比较合适。
1.2.2 建立状态转移概率矩阵
假设P(m)ij是状态i到j的m步转移概率,M(m)ij是状态i到状态j的m步转移次数,Mi属于i个状态的数量,状态转移概率矩阵如式(8)所示

1.2.3 计算预测值
假设时间序列在(k)时刻处于状态j,根据状态j的残差区间[ωj-,ωj+]的中值,与灰色预测值(0)(k),可以得出灰色马尔科夫链模型的预测值为(k+1),如式(9)所示
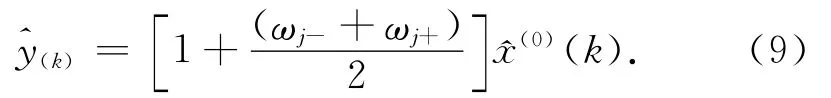
1.3 对模型精度的检验
灰色预测模型建立以后,对模型的实用性以及模型的精度进行验证。GM(1,1)模型通过计算残差、平均相对误差、均方差比值、小误差概率等指标后,查找灰色预测模型精度检验等级表(见表1),从而可以判断模型的精度等级。计算过程和算式如下:
1)分别计算出原始数据序列的残差ε(k),相对误差Δ(k)与平均相对误差

2)分别算出原始数据与残差的标准差S1,S2。根据S1,S2分别算出均方差比值C和小误差概率P


表1 灰色模型的精度检验表
2 案例分析
利用马尔科夫链对灰色GM(1,1)模型的预测误差进行修正,以乌鲁木齐市2007~2013年的伤亡人数为基础,对乌鲁木齐市2014~2016年的交通事故伤亡人数进行预测。
2.1 建立GM(1,1)预测模型
灰色GM(1,1)模型的建立过程如下:
1)原始数据序列为:x(0)={1 047,1 068,872,902,876,846,895};
2)对数据进行累加得:x(0)={1 047,2 115,2 987,3 889,4 765,5 611,6 506};
3)建立均值生成序列z(1)(k),z(1)(k)={1 581,2 551,3 438,4 327,5 188,6 058.5},矩阵Y与B为
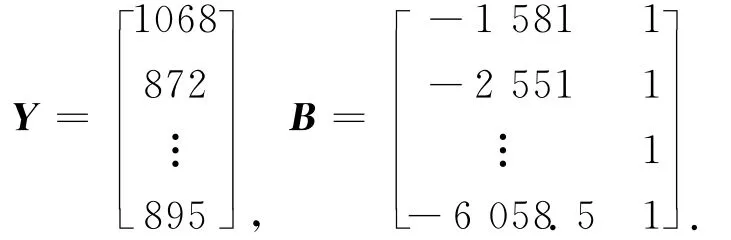
4)对参数进行最小二乘估计,得出a与b的值
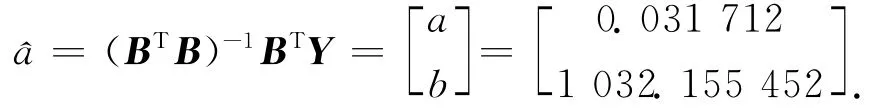
5)将a和b的值带入式(6),得出模型如式(17)所示

根据式(17),并根据式(6)还原数据,得出乌鲁木齐市2007~2013年的伤亡人数灰色预测值,结果如表2所示。预测结果显示,模型的预测值是单调递减的,2008年和2009年的模型相对误差较大,分别为7.96%和-9.29%。最后可得到2014~2016年伤亡人数灰色预测值分别为813人、788人、763人。

表2 乌鲁木齐市交通事故实际伤亡人数与灰色模型预测值的对比
6)对GM(1,1)模型进行精度检验。利用式(10)~式(16)可以算出,平均相对误差为4.32%,后验差比值为61.34%,小误差概率为0.714 3。查找表1,可知该模型的精度为3级,说明可以用于交通事故预测,但精度较低,需要进一步优化来提高模型的精度。
2.2 建立马尔科夫链模型
2.2.1 状态划分
因为本研究样本数量较少,按照均值划分,误差可分为三个状态,分别用E1、E2、E3表示,如表3所示。

表3 死亡人数状态划分表
根据表3中的状态划分情况,可以把2007~2013年交通事故伤亡人数进行状态划分,结果如表4所示。
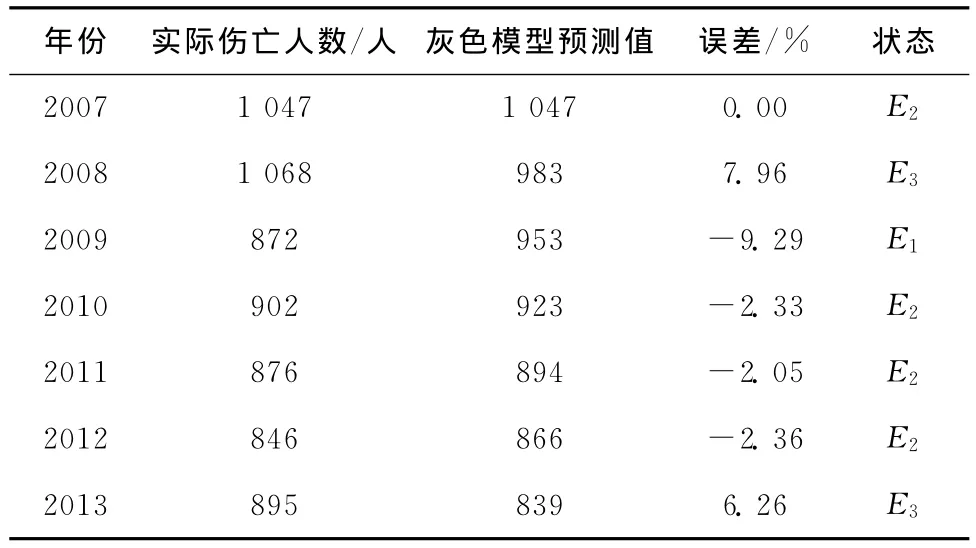
表4 乌鲁木齐市2007~2013年交通事故实际伤亡人数状态划分情况
2.2.2 构建转移概率矩阵
由式(8)计算出一步,两步,三步转移概率矩阵

2.2.3 计算预测值
利用式(9)对2007~2013年乌鲁木齐市伤亡人数进行拟合。例如2008年的灰色预测值为983,处于状态E3,=983× [1+0.5× (2.21% +7.96%)],可以得出2008年的灰色马尔科夫链预测值为1 033人。同理,可以得出其余年份的预测值,两种模型的残差和误差情况如表5所示。可知,2008年和2009年的灰色GM(1,1)预测值相对误差为7.96%和-9.29%,而灰色马尔科夫链GM(1,1)预测值和相对误差降到3.28%和-2.29%。从图1可知,灰色GM(1,1)模型的预测值呈一条平滑递减曲线,而灰色马尔科夫链GM(1,1)模型的预测值具有一定的波动性,接近伤亡人数的实际值,预测结果更加可靠。
根据表4可知,2013年伤亡人数预测值处于状态E3,初始行向量为V0=(0,0,1)。因此,R(1)·V0=(1,0,0),说明2014年处于状态E1,再利用式(9)预测出2014的伤亡人数为761人。同理,可以预测2015年、2016年伤亡人数年所处的状态及预测值,结果如表6所示。

表5 灰色GM(1,1)模型与灰色马尔科夫链GM(1,1)模型预测结果

图1 两种模型的预测结果对比

表6 GM(1,1)模型与灰色马尔科夫链预测模型对2014~2016年伤亡人数预测值
2.2.4 对灰色马尔科夫链 GM(1,1)模型进行精度检验
利用马尔科夫链对灰色模型进行误差修正后,平均相对误差(越小越好)从4.32%降到1.67%,降低了2.65%;后验差比(越小越好)从61.34%降到22.04%,降低了39.3%;小误差概率(越大越好)从0.714 3提高到1,提高了0.285 7。查找表1,可知该模型的精度变为一级(好),说明灰色马尔科夫链GM(1,1)模型的预测精度比单一的灰色 GM(1,1)模型高,因此,交通事故预测值更加可靠。
3 结 论
1)首先建立了灰色GM(1,1)模型,以乌鲁木齐市2007~2013年交通事故伤亡人数为基础,对2014~2016年乌鲁木齐市交通事故伤亡人数进行了预测。模型的预测精度较低,平均相对误差较高(4.32%),精度等级仅为三级,模型预测精度仍可提高。
2)利用马尔科夫链,建立灰色马尔科夫链模型,通过均值状态划分、建立状态转移概率矩阵,对灰色GM(1,1)模型的预测误差进行了修正,模型的预测精度有了明显提高,平均相对误差降到1.67%,降低了2.65%,模型的精度等级提高到了一级。说明灰色马尔科夫链模型比单一的灰色模型更加可靠,预测结果更接近实际。
3)通过对乌鲁木齐市未来交通事故伤亡人数的预测,可为今后乌鲁木齐市交通事故的预防提供有力的理论依据。
[1] 王炜.道路交通工程系统分析方法[M].北京:人民交通出版社,2008.
[2] 董四辉、史卓屾.道路交通事故BP神经网络预测研究[J].中国安全科学,2010(9):15-20.
[3] 邓聚龙.灰色系统基本方法[M].武汉:华中理工大学出版社,1996.
[4] 刘思峰.灰色系统理论及其应用[M].7版.北京:科学出版社,2014.
[5] 刘建齐.道路交通事故预测中的灰色预测GM(1,1)模型[J].广西交通科技,2003(4):106-109.
[6] 李相勇.道路交通事故灰色马尔科夫预测模型[J].中国安全科学学报,2008,18(3):33-36.
[7] 杨晓松,张双成.新陈代谢GM(1,1)模型在建筑物沉降监测中的应用[J].交通科技与经济,2014,16(5):100-102.

