具有承载能力约束的装箱问题的蚁群算法
张晓蕊,刘向东
(大连民族学院计算机科学与工程学院,辽宁大连116605)
三维集装箱问题[1]是将一系列规则的长方体以最佳方式装入到集装箱的过程,是货物运输过程中重要的环节。过去的几十年中,在处理集装箱装入方面已经取得了很大的进步,人们已经研究出了能够解决集装箱装入问题的一些方法,比如模拟退火算法[2,3]、遗传算法[4,5]、禁忌搜索算法[6,7]、树搜索算法[8,9]等等。基于这些算法在装入货物的时候,人们通常是将集装箱的整体空间划分成一些规则的空间,然后再将其余的货物进行装入,使得装入货物后的剩余空间继续划分成更小的规则空间。但是在实际的运输过程中,装箱问题还会受到许多实际条件的约束[10]和影响,比如货物摆放的方向要受到限制、货物所承受的最大压力要受到限制、货物的底面要有足够的支撑、相同类型的货物或同一批次的货物要放在一起等等,这些约束都影响着运输的质量和货物的装箱率。
本文以装箱系统为研究背景,目的是在装箱过程中减少货物的破损率和提高货物的装箱率,设计出寻优能力很强的蚁群算法,将运输过程中较重要的稳定性约束和承载力约束加入到其中。该算法与实际装箱问题相结合,能够满足货物装入过程中所需要的约束条件,具有很强的实用性。
1 问题定义
本文采用的是单箱问题,集装箱是右侧开口的规则长方型,将其定义在一个三维坐标系下,其中,坐标系的原点为集装箱的左-前-下顶点,集装箱的长、宽、高分别沿着坐标系的X轴、Y轴、Z轴的正方向。
问题可以简单描述为:在一个长、宽、高分别为L、W、H的长方体集装箱内,装入长、宽、高分别为li、wi、hi(i=1,2…m)的 m 种货物。其中,每类货物都是由尺寸相同的多个长方体组成。目的是使装入货物的总体积最大,集装箱的空间利用率最高,但是该问题还需要满足三种基本约束[10]:
(1)待装货物必须都能装入集装箱内部;
(2)货物之间互不重叠;
(3)已装入的货物边缘要与集装箱的边缘平行。
2 空间处理
2.1 空间划分
由于不同的空间划分将会影响到集装箱的空间利用率。因此,在解决集装箱装入问题中,空间划分是一个重要因素。为了满足装入过程中的各个约束条件,不规则的装入空间需要划分成规则的装入空间。当货物被装入到剩余空间后,该空间被拆分成三个子空间,即前面的空间、上面的空间、右面的空间。两种基于稳定性的空间划分方法如图 1[11]。
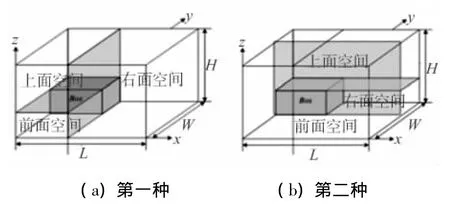
图1 稳定性空间划分
2.2 空间合并
随着货物的装入,零碎空间变得越来越多,使得大尺寸的货物无法装入。空间的划分采用虚拟切割原理,实际上剩余空间还是相通的。因此,有必要对剩余空间进行合并。采用队列结构来存储已装不下任何货物的废弃空间。考虑分别对剩余空间和废弃空间这两类空间进行合并处理。
根据两种稳定性空间划分方法能够保证货物的稳定性要求,对于空间合并,我们只需要考虑相同高度即可。合并原则是使合并后的空间底面积要比合并前的任一空间的底面积都要大[3]。
3 承载力约束
本文主要实现关联约束、稳定性约束和承载能力约束,目前大多的研究方法都未将货物的承载能力约束考虑进去,只有少数的将承载力约束考虑在内[11]。本文采用第一种和第二种空间划分方法就可以保证货物的稳定性。对于关联约束,将相同类型的货物以组合块的形式进行装入,这样就保证了货物的关联性。而对于较难实现的承载力约束,本文提出了一个将承载能力约束与空间划分相结合的新方法。随着货物的不断装入,每个划分的空间都带有了一个承载力值,通过空间的承载力值来判断剩余的货物是否能够放入。空间承载力的产生和变化都是随着货物的不断装入而产生和变化的。可见,货物承载力的表示是解决空间承载力的基础。本文采用货物单位面积所能承受的最大重量来表示货物的承载力,表示为:

式中,li、wi是第i种货物的长和宽,Gi是货物的重量。
当有一个货物需要装入时,需要判断当前货物的重量是否小于或等于下面货物的承载能力,根据当前空间承载力来判别货物是否能装入该空间,其装入条件判别可以表示为:

式中,Bspace表示当前空间的承载力。
当多个货物装入到空间后,空间的承载力会发生变化,而上面空间的承载能力等于该空间的承载力值减去货物本身的承载力值,即:

由于货物装入时会出现分层的现象,为了避免货物被压坏,空间承载力的大小则要选取空间承载力和货物本身的承载力中的最小值,即:
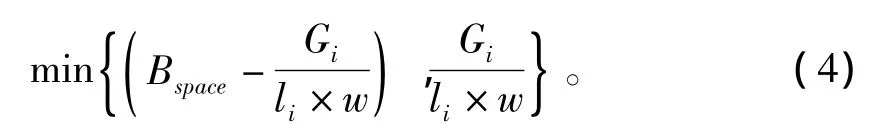
当进行空间合并时,承载力也会发生变化,此时合并后的空间承载力要选取合并前空间承载力的最小值,即:
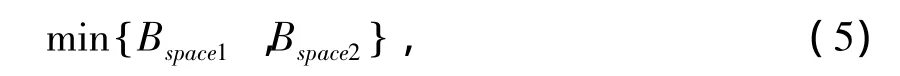
式中,Bspace1、Bspace2是两个空间的承载力。
本文货物是以组合的方式进行装入的,这样就要求货物要以相同的摆放方式进行组块,以便于计算出装入空间中的货物个数。当货物被装入前,需要判断组合块的承载力是否小于等于空间的承载力,组合块的承载力可以表示为:

式中,m是组合块的层数。
4 蚁群算法
4.1 初始解
为了提高体积利用率,优先装入大尺寸货物。在蚁群算法中,一个好的初始解能够加快寻优速度。按货物最长边排序;按货物的底面积排序。本文将货物按体积从大到小进行排序。
货物编码是蚁群算法应用成功与否的关键。货物种类按1到n进行编号,同类货物编号相同,不同种类的货物编号不相同。此时n种货物对应放在n个节点上,这样把待装货物编成了一个解的序列,即:
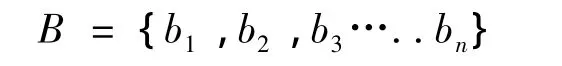
式中,n为待装货物的种类数;bi是每种货物的编号,该值为整数。通过信息素对其进行操作实际上就是改变待装货物的排放顺序,从而产生不同的解序列。
4.2 参数设置
(1)信息量
依据每个货物上所留下的信息素的量来确定将会被选择的货物。通过更新信息素来更新蚂蚁的路径。当蚂蚁完成从货物i到货物j的搜索或者遍历完所有种类的货物后,每种货物上的信息素将会挥发。
蚁群觅食时,信息量越多距目标越近。在货物j上留下的信息素的量代表着货物j被选择的可行性概率,它决定了蚂蚁的移动方向。
当蚂蚁完成从货物i到货物j的一次搜索后,就会在货物i和货物j上释放信息素。信息量影响着蚂蚁的搜索路径。在初始时刻,将ant_m只蚂蚁随机的放到n类货物上,
此刻每种货物上的信息量是相同的,即τi(0)=C(C为常数)。当蚂蚁完成对每类货物的遍历后,每种货物上的信息量按式(7)进行更新。
(2)概率转移函数
第k只蚂蚁根据每种货物上的信息量来确定其移动的方向(k=1,2,…,ant_m)。用来表示第k只蚂蚁移动到货物i时,选择货物j的概率。概率转移函数按式(10)进行表示:

式中,τj是在货物j上的信息量,τs是刻遍历一次所有蚂蚁在该货物上留下的信息素的总量。
(3)评价函数
蚁群算法的可行性接是通过一个评价函数获得的。一般情况下,对于启发式算法的评价函数能够处理多目标,多约束问题。在本课题中,蚁群算法的评价函数将集装箱的空间利用率作为唯一目标,同时,货物的稳定性将考虑在这个装入过程中。评价函数表示为:
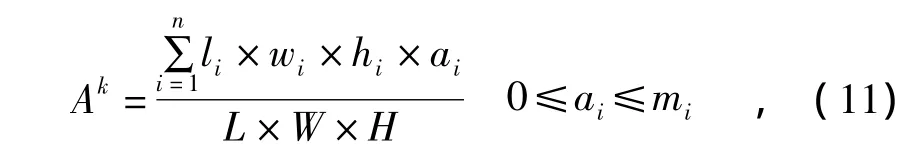
式中,L×W×H是集装箱的容量,n为货物的种类数,ai为每种类型的货物装入数,mi为每种类型的货物数。
4.3 货物装入
编码表示一种装入顺序,每种装入顺序产生一种布局。在装入过程中,对剩余空间进行排序,采用栈结构来存储剩余空间,栈的初始状态是空的集装箱,弹出的栈顶元素为每次货物要装入的空间。初次装入的剩余空间是整个空的集装箱空间,当货物装入时,将其放在当前剩余空间的左-下-后角,此时该剩余空间被分成三个子空间,按照前面空间,上面空间,右面空间这个顺序压入剩余空间的栈中,此次装入结束;下次装入货物时,栈顶元素弹出,作为新的装入空间,重复上述过程,直至集装箱没有可利用的剩余空间或是货物已全部装入。在此过程中,每次要装入一个货物时,都要判断该货物是否满足当前空间的最大承载力。如果满足,则装入该货物;如果不满足,就装入下一货物。每次剩余空间都要与废弃空间进行合并。
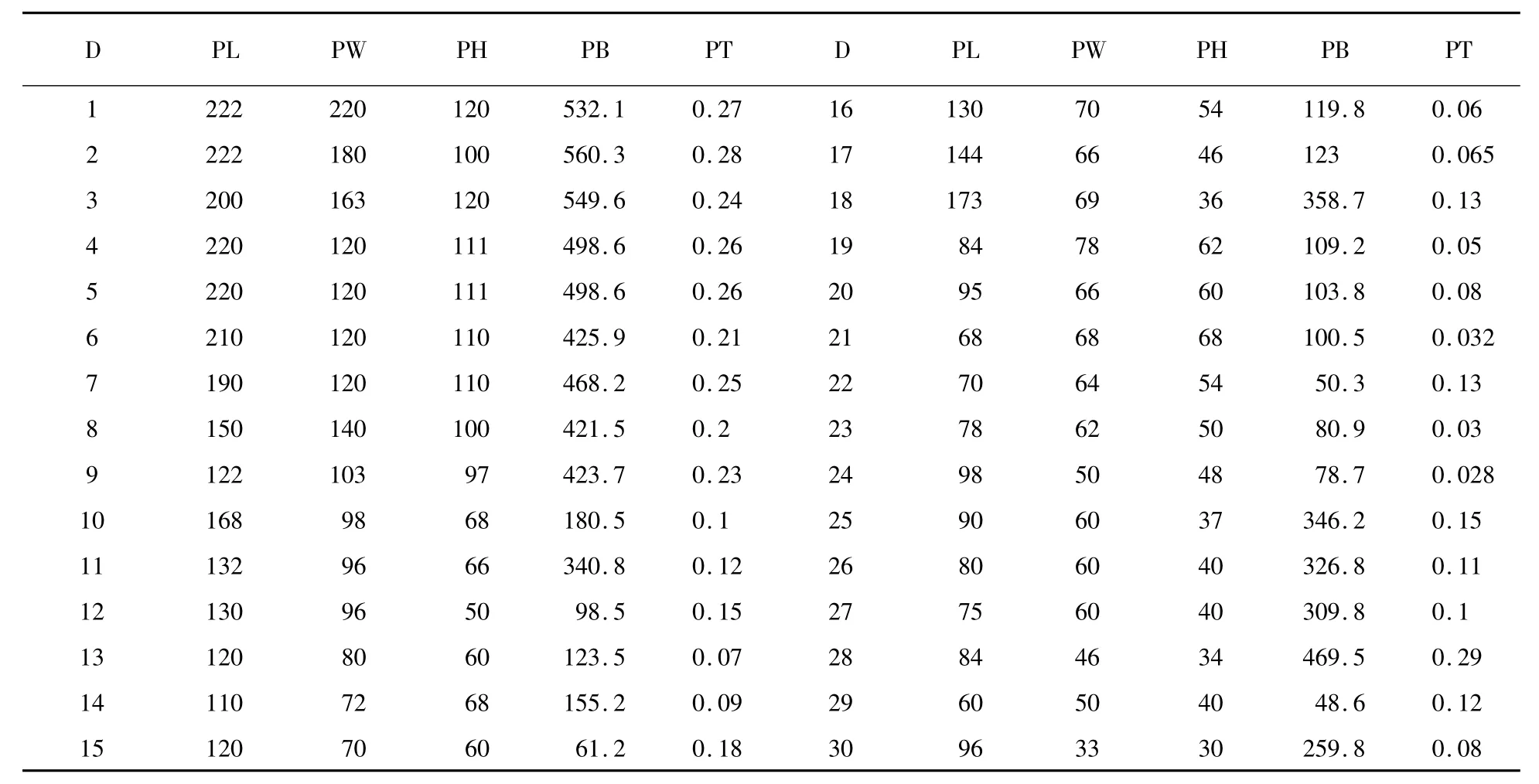
表1 待装货物尺寸
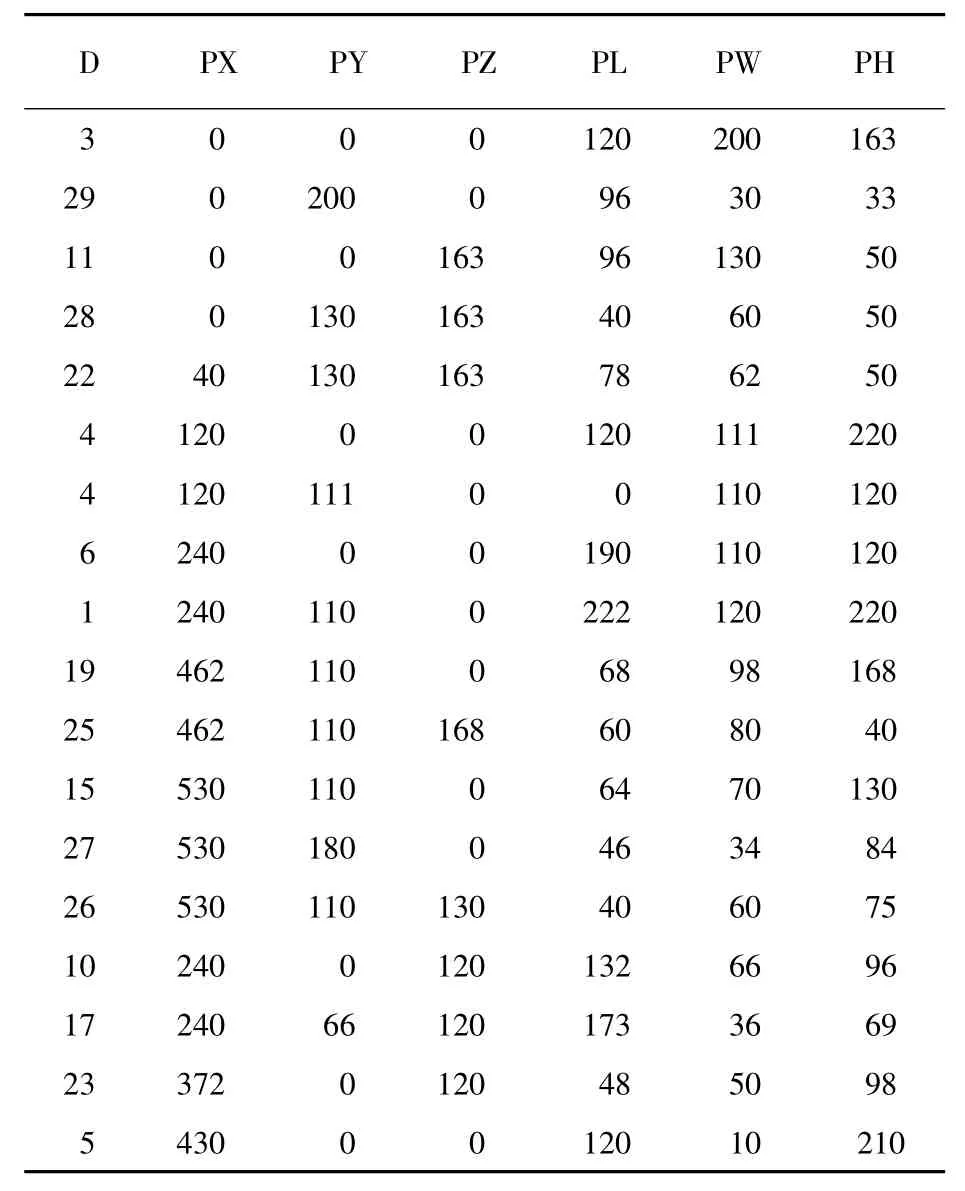
表2 货物装入位置数据
5 测试结果比较
本文算法采用文献[12]中提出的一组测试数据见表1。布局空间为国际标准集装箱,尺寸为L=589.9 cm,W=238.8 cm,H=235.2 cm。在考虑承载能力约束和稳定性约束的情况下,与文献[13]采用的禁忌搜索算法相比较,禁忌搜索算法得到了82.87%的利用率,而本算法却得到了85.31%的利用率见表2,装入效果图如图2。由此可见,本算法的性能优于禁忌搜索算法。
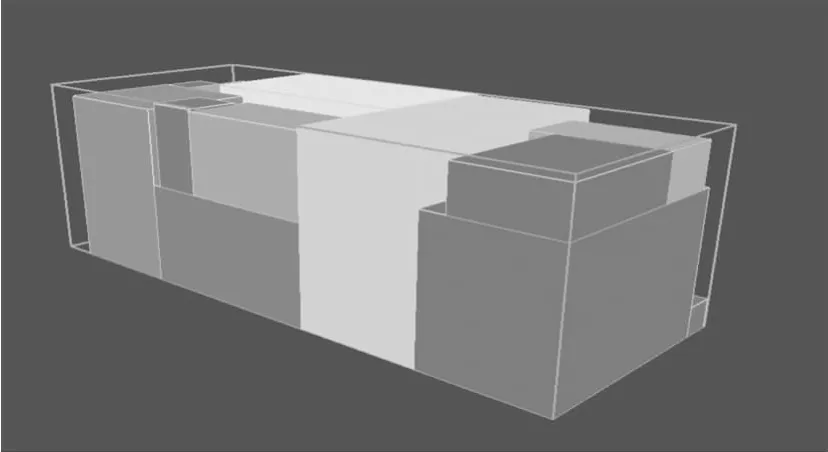
图2 装入效果图
6 结束语
对具有承载能力约束的集装箱装入问题进行了研究,提出了针对三维装箱问题的蚁群算法,并给出了承载能力约束的表现形式和定义。在货物装入的过程中,判断货物的承载能力是否满足要求来进行货物装入,成功的将承载能力约束和蚁群算法相结合。实验结果表明,该算法能够保证货物在装入过程中的稳定性,同时还防止了货物被压坏的情况,便于实际应用。另外,还为基于蚁群算法求解三维装箱问题提供了基础和经验。
[1]周昕,纪颖.三维装箱问题的遗传算法研究[J].电脑学习,2010,6(3):117-118.
[2]DERELI T,G S DAS,A hybrid simulated annealing algorithm for multi-objective container loading problems[J].Applied Artifical Intelligence,2010,24:463-486.
[3]张德富,彭煜,朱文兴.求解三维装箱问题的混合模拟退火算法[J].计算机学报,2009,32(11):2147-2156.
[4]邢斌,杨信廷,钱建平,等.基于遗传算法的规则包装农产品三维装箱模型[J].农业工程学报,2011,27(8):237-241.
[5]HASNI H,SABRI H.On a hybrid genetic algorithm for solving the container loading problem with no orientation constraints[J].J Math Modeling Algorithms,2012(11):1032-1041.
[6]刘嘉敏,董宗然,黄有群集装箱装箱问题的同质块禁忌搜索算法[J].高科技通讯,2011,21(8):817-823.
[7]LIU J M,YUE Y,DONG Z R,et al.A novel hybrid tabu search approach to container loading[J].Comput Oper Res,2011,38:797-807.
[8]陆佳炜,肖刚,高飞.基于装箱树算法求解集装箱装载问题的研究[J].浙信息与控制,2007,36(5):644-648.
[9]BORTFELDT A,JUNGMANN S.A tree search algorithm for solving the multi-dimensional strip packing problem with guillotine cutting constraint[J].Ann Opera Res,2012,196:53-71.
[10]刘晓楠.基于重量约束的集装箱装入问题的研究[D].沈阳:沈阳工业大学,2009.
[11] QUEIRA L J,MORABITO R,YAMASHITA D S.Three dimensional container loading models with cargo stability and load bearing constraints[J].Computer and Operations Research,2012,39:74~85.
[12]姜义东,查建中,何大勇.集装箱装载矩形货物的布局研究[J].铁道学报,2002,22(6):13-18.
[13]刘嘉敏,刘晓楠,黄有群.具有承载能力约束的集装箱装入问题的求解方法[J].计算机工程与设计,2009,30(22):5204-5207.

