湿陷性黄土的微结构参数

王秀伟，高凌霞，武志东

(大连民族学院土木建筑工程学院辽宁大连116605)

湿陷性是黄土最为重要的工程性质，大量的研究表明，黄土的微观结构是表征黄土湿陷性的一个重要质量指标［1-6］。在黄土微结构研究中，近年也取得了不少成果。尹亚雄［7］等采用扫描电镜、数字图像方法和表面积孔隙分析仪研究了天然黄土和不同固化龄期加气硅化黄土的微结构和孔隙特征，Hu［8］等研究了黄土在动荷载压密条件下的力学性能和微结构变化。倪万魁［9］通过对洛川黄土在反复冻融作用下的电镜扫描观测、单轴压缩试验和三轴剪切试验，研究了冻融循环作用对黄土微结构和强度的影响。王慧妮等［10］基于计算机X射线断层术与扫描电镜图像对黄土微结构进行了定量分析。周阳等［11］利用改进的边缘检测算法，对黄土微结构SEM图像进行检测，该方法可以有效地去除虚假边缘，区分黄土颗粒形态，从而更清晰地揭示其内部物质的结构。

综上所述，基于扫描电镜(SEM)的土体微观结构研究是当前岩土工程中最有效、最直接的方法。本文针对原状黄土进行了湿陷性试验，SEM试验，从中提取微结构参数，并对各参数间的相关关系进行统计分析。

1 黄土的湿陷性及电镜扫描试验

1.1 湿陷性试验

试验用土取自西安黄土塬区，取样深度为2.0 m，原状试样。天然密度为 1.56 g.cm-3，土粒相对密度为 2.71，天然含水率为17.4%。采用单线法实验确定黄土的湿陷性，实验结果见表1。

表1 天然含水量土样湿陷试验

1.2 SEM 试验

采用扫描电镜(scanning electron microscopy)获取湿陷前后黄土的微结构照片。扫描电镜被广泛用来观察土的微观结构形态。本次试验采用的扫描电镜，不需干燥土样，可以在自然状态下观察土样的结构，这样可减小对土样的扰动。不同压力作用下黄土湿陷前后的微结构照片如图1。共获得10幅湿陷前SEM照片和11幅湿陷后的照片。共21幅SEM照片组成的黄土样本进行了域微结构分析。

图1 湿陷前后的微结构SEM照片对比(左侧为湿陷前的照片)

2 黄土微结构参数的相关分析

2.1 SEM图像微结构参数的提取

对由10幅湿陷前SEM照片和11幅湿陷后的照片，共21幅SEM照片组成的黄土样本进行了域微结构分析。采用Leica QWin系统可以提取到两类微结构参数，域(Field)微结构参数和特征(feature)微结构参数［11］。本文针对9个域微结构原始参数进行研究。为了使得到的数据具有可比性和一般性，对所有照片的信息提取针对同一分析域进行，分析域的位置和大小(1200 μm×800 μm的矩形区域)如图2。

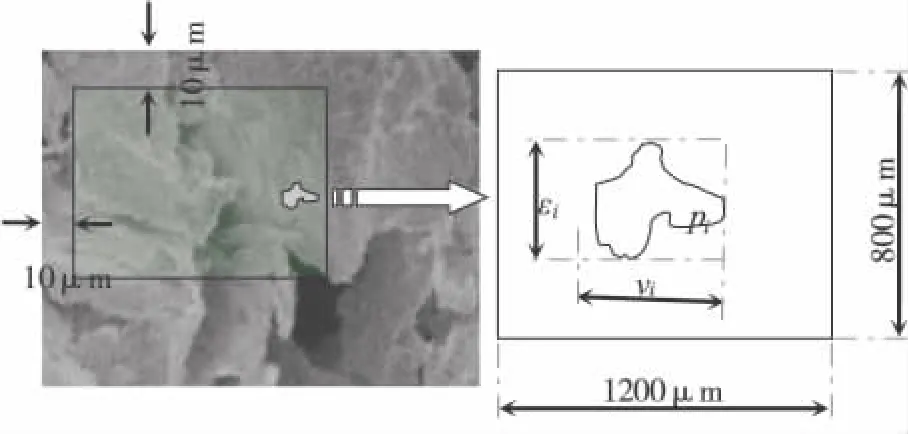
图2 SEM照片的研究域及参数定义

其中pi表示第i个孔隙，其水平截距为εi，垂直截距为νi，单位是像素，对于本分析过程，1μm=20像素。微结构参数提取后，每一个孔隙体对应一个9维向量。其中x1为水平截距，表示所有孔隙水平投影的长度之和，即x1=Σεi;x2为垂直截距，表示所有孔隙垂直投影的长度之和，即x2=Σνi;x3为所有孔隙的周长之和;x4为孔隙总数;x5为总孔隙面积百分比;x6为各向异性系数;x7为填充比;x8为平均弦;x9为图像处理系统自动计算得到的256灰度自适应阈值。这些参数，从整体上反映了域内的孔隙体大小、形状、级配、各向异性等微结构参数，基本刻画了孔隙体微结构的所有信息。

2.2 微结构参数间的相关性研究

(1)简单统计量

9维微结构参数可以表示为向量形式，即

得到的微结构参数的简单统计量见表2。

表2 各参数的简单统计量

(2)Pearson相关系数矩阵

由于9维微结构参数之间可能存在某种相关关系(包括正相关和负相关)，为了研究这种相关性是否显著，有必要考察参数间的相关系数矩阵。9维微结构参数之间的协方差矩阵可以表示为

将21组9维微结构参数代入式(4)和式(5)，经过计算最终得到的协方差矩阵可以表示为

任意两参数xj、xk之间的相关系数可以表示为

式(8)称为Pearson相关系数矩阵，计算结果为

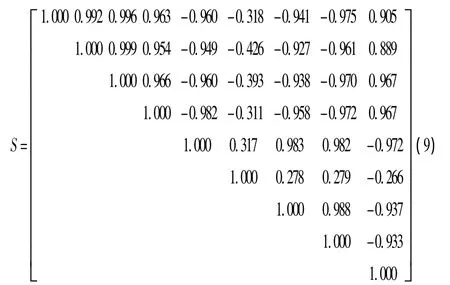
为判断各参数之间是否相关，还要进行假设检验

给定显著性水平α=0.0001，假设x为来自9维正态总体的一个样本，根据统计学原理，如果H0为真，则

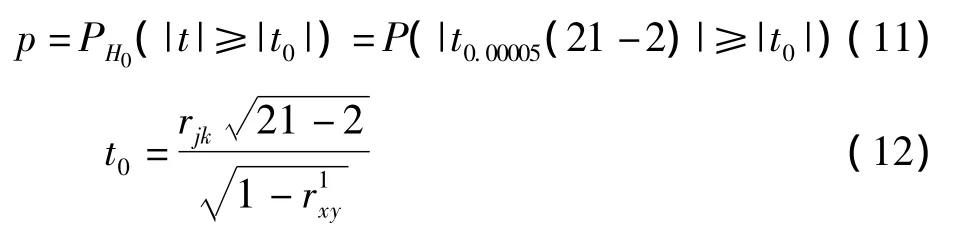
当p＜α时，拒绝H0，否则接受H0。检验结果表明p16=0.1595，p26=0.0541，p36=0.0778，p46=0.1697，p56=0.1621 和p67=0.2218，p68=0.2205，p69=0.2432，均满足p＞ α，说明二者之间的相关性不显著。而对于其它各参数之间的相关系数，均满足p＜α，说明它们之间的相关性高度显著。

(3)Spearman相关系数矩阵

微结构参数xi(i=1、2、…、9)是容量为21的一维样本，即xi1、xi2、…、xin、…、xi21。其顺序统计量为xi(1)、xi(2)、…、xi(m)、…、xi(21)，若xin=xi(m)，则称m是xin在样本观测值中的秩，记作Rin，并称Rin是第n个秩统计量。如果有多个大小相等的观测值，其秩则为应排序位置的平均值。

根据上述方法，可以得到xi(i=1、2、…、9)的21个秩统计量。根据这些秩统计量，9维微结构参数可以改写为以秩统计量表述的9×21矩阵。Spearman相关系数为秩统计量之间的相关系数，可以根据式(4)、式(5)和式(7)计算得到，但需要以Rin代替原始微结构数据。类似于Pearson相关系数矩阵，可以定义Spearman相关系数矩阵。即

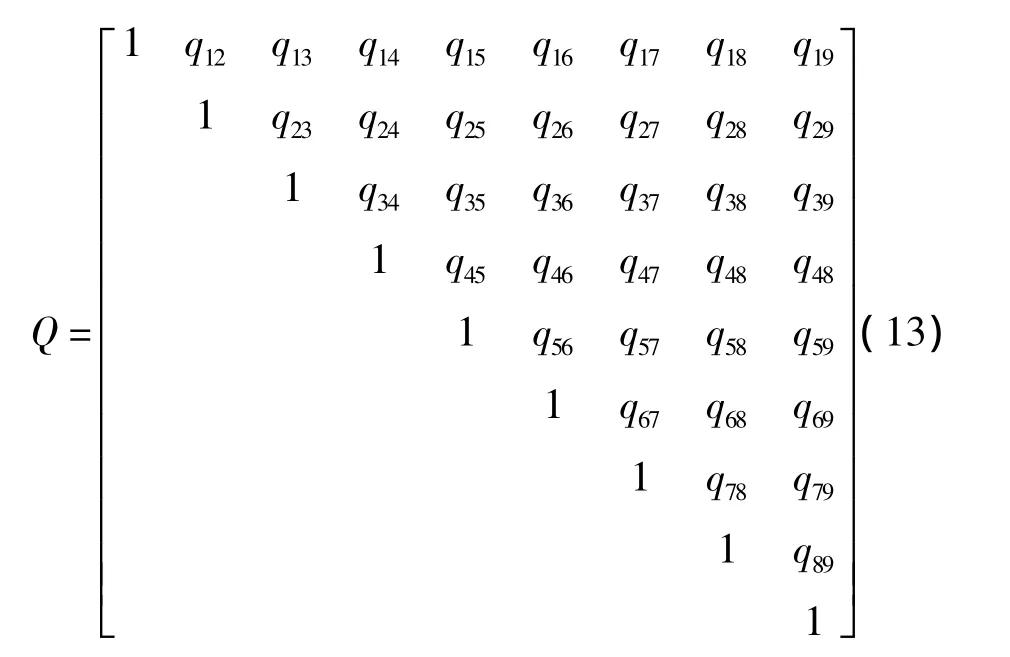
与Pearson相关系数矩阵相比，Spearman相关系数矩阵似乎损失了某些信息，但它适用于研究具有一般分布的多维总体，且对有异常值的观测数据，具有耐抗性。也就是说，个别数据的异常不会影响整体判断结果。将原始参数代入以上各式，计算得到原始微结构参数的Spearman相关系数矩阵由式(14)表示。

同样，给定显著性水平α=0.0001，则当p＜α时，拒绝H0，否则接受H0。检验结果表明p16=0.1228，p26=0.0238，p36=0.0432，p46=0.1244，p56=0.0896 和p67=0.0951，p68=0.1258，p69=0.1655，均满足p＞α，说明二者之间的相关性不显著。而对于其它各参数之间的相关系数，均满足p＜α，说明它们之间的相关性高度显著。这与前文Pearson相关系数的计算和检验结果是完全一致的。

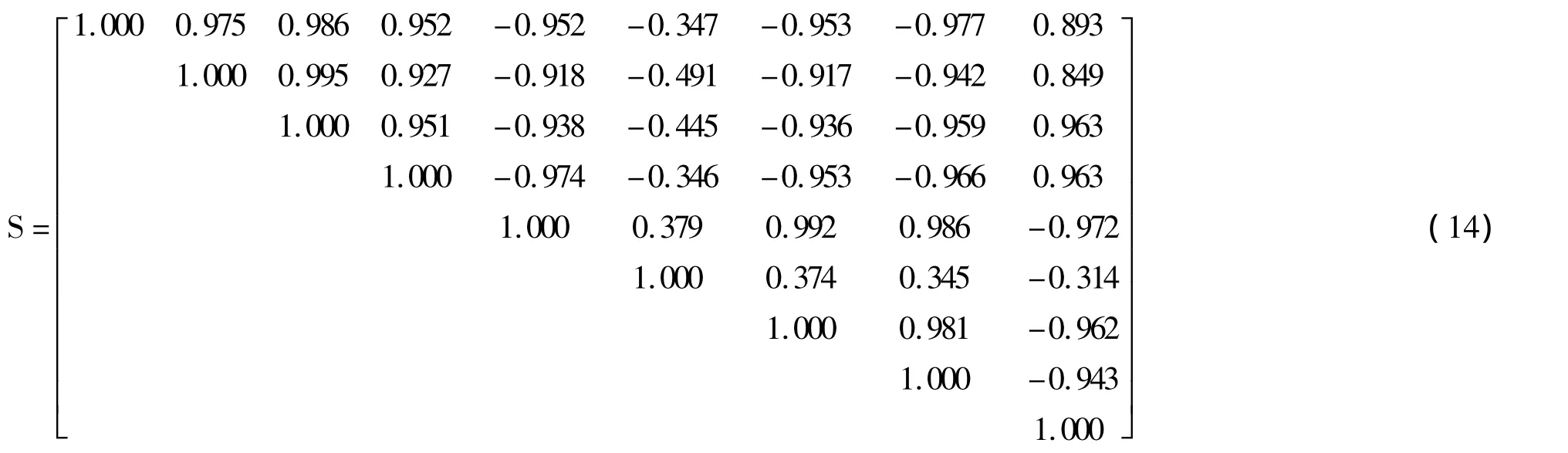
由统计学得知，样本数据的均值向量、协方差矩阵S及Pearson相关系数矩阵R，分别是总体的均值向量¯x、协方差矩阵和相关系数矩阵的相合估计。而Spearman相关系数矩阵Q，则是总体相关系数矩阵的一个稳健估计。

3 结论

两种相关分析的结果均表明，在所有孔隙体微结构参数之间，只有孔隙总面积和灰度自适应阈值之间的相关性不显著，而其他参数之间的相关性均比较显著。因此得出结论，在反映黄土微结构特性方面，提取到的参数有较多“重复”的信息。因此，在将土微结构参数引入土的本构模型中时，可以采用主成分分析，以消除这些“重复”，以降低参数的维数。

［1］谢定义.黄土力学特性与应用研究的过去、现在与未来［J］.地下空间，1999，(4):273-284.

［2］胡瑞林，李向全，官国琳，等.土体微结构力学-观念·观点·核心［J］.地球学报-中国地质科学院院报，1999，20(2):150-156.

［3］刘祖典，张伯平.关于黄土和黄土状土湿陷性评价问题［J］.西北农学院学报，1979，(03):37-48.

［4］高国瑞.黄土显微结构分类与湿陷性［J］.中国科学，1980，(12):1204-1208.

［5］高国瑞.中国黄土的微结构［J］.科学通报，1980，(20):945-948.

［6］邵生俊，周飞飞，龙吉勇.原状黄土结构性及其定量化参数研究［J］.岩土工程学报，2004，26(4):531-536.

［7］尹亚雄，王生新，韩文峰等.加气硅化黄土的微结构研究［J］.岩土力学，2008，29(6):1629-1633.

［8］HU R L，YEUNG M R，LEE C F，et al.Mechanical behavior and microstructural variation of loess under dynamic compaction ［J］.Engineering Geology，2001，59(3-4):203-217.

［9］倪万魁，师兴强.冻融循环作用对黄土微结构和强度的影响［J］.冰川冻土，2014，36(4):922-927.

［10］王慧妮，倪万魁.基于计算机X射线断层术与扫描电镜图像的黄土微结构定量分析［J］.岩土力学，2012，33(1):243-254.

［11］周阳，王凤，马逢清，等.基于改进边缘检测算法的图像处理技术应用［J］.工业控制计算机，2013，26(3):73-77.