轮式驱动电动汽车驱动系统仿真
宋 鹏,薄纯娟,徐国凯,张 涛
(大连民族学院机电信息工程学院,辽宁大连116605)
日益严重的环境问题和能源危机使百年交通工具——汽车面临着越来越严峻的考验。电动汽车以电力为主要动力,它可以实现零排放或极低排放,在行驶过程中没有污染,热辐射低,噪音小,因而受到广泛的欢迎。目前,大部分电动汽车的研发主要是对传统燃油汽车进行动力改造,基于一个动力电动机,通过减速器和差速器驱动两个(或四个)驱动轮[1-2]。相比传统电动汽车而言,轮式驱动电动汽车具有车身结构简单、车身重量轻、传动效率高的优点,而且可以分别控制每个驱动轮的运行参数,如转速、转矩等,轮式驱动电动汽车由于其运动控制、结构布置等方面的优势,成为电动汽车研究热点。
1 轮式驱动电动汽车驱动系统
轮式驱动电动汽车驱动系统是一个全新的驱动系统,由电动机直接驱动车轮,省掉了离合器、变速器及传动轴等传动环节,消除了传动中的机械磨损与损耗,提高了传动效率,相比之下具有较小的体积和较轻的重量,同时故障率降低,且在提高效率的同时,车轮空间也能得到有效利用[3]。轮式驱动电动汽车驱动系统结构图如图1。系统取消了差速器和半轴,将行星减速器与电动机制造为一体,称为电动轮,轮胎直接安装在电动轮上。电机控制器接收速度给定(踏板)、制动(踏板)、PDRN(停车、倒车、空档、前进)信号控制电机旋转,驱动车轮运动。
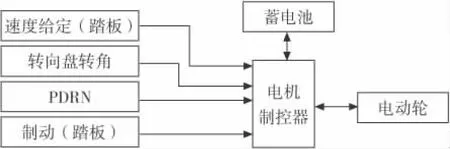
图1 驱动系统结构图
2 数学模型的建立
2.1 电机数学模型的建立
本文选用直流电机作为电动汽车驱动电机,对于直流电机的建模可以由电机的简易电路图建立数学方程,假设电机的主电路电流连续,并且磁通量恒定,则可得到如下方程:
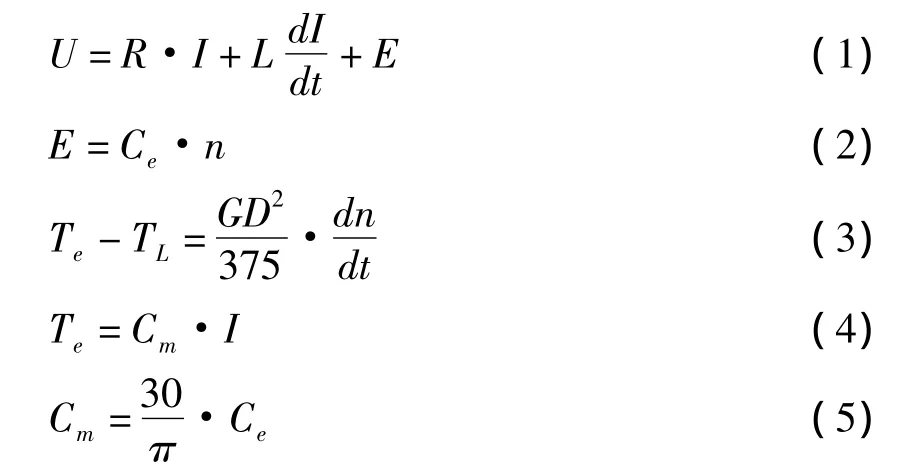
式中,R表示电枢回路的电阻,L表示电感,U表示电机两端电压,I表示电机回路电流,E表示感应电动势,n表示转速,TL表示负载转矩,Cm表示转矩电流,GD2表示飞轮力矩。
2.2 轮胎数学模型的建立
轮胎受力如图2,轮胎力学模型目前仍处于不很精确的状态,本文采用统一半经验指数轮胎模型,其方程式如下[4-5]:
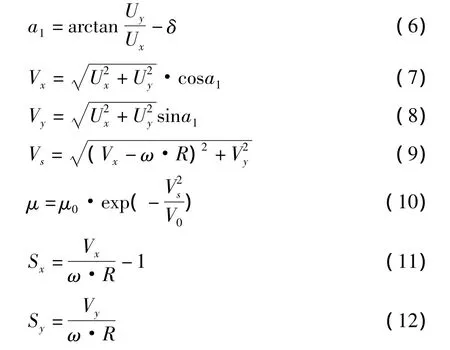
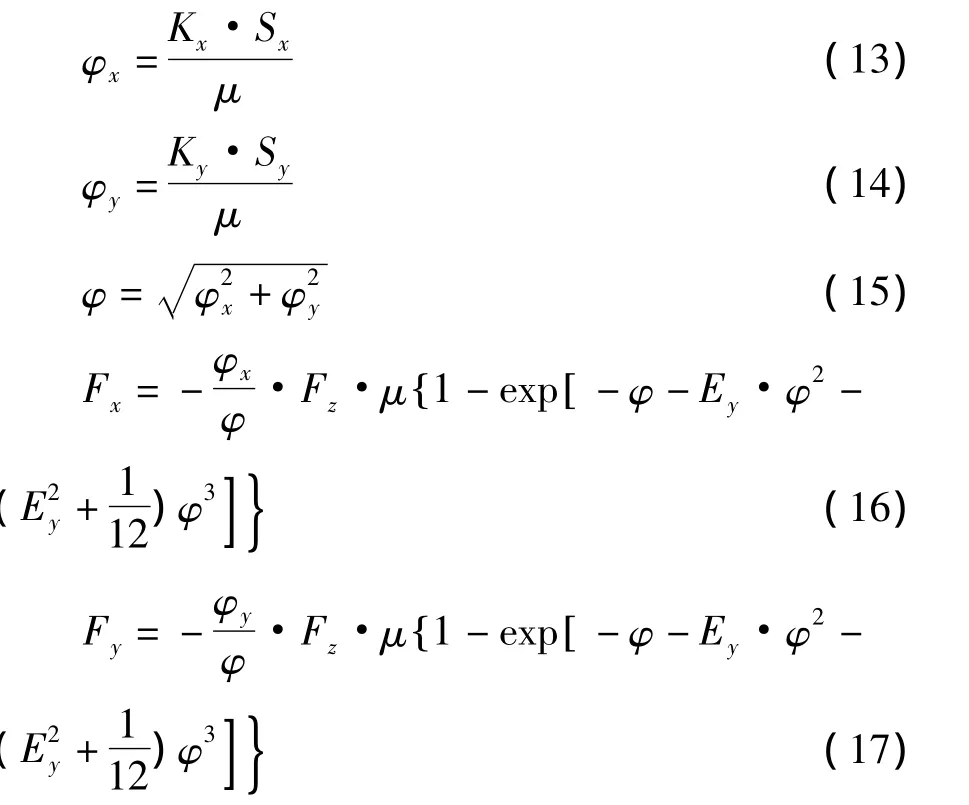
式中,a2表示轮胎侧偏角;δ表示转向角,值为零时表示非转向轮;Ux表示车轮中心的纵向速度;Uy表示车轮中心的侧向速度;Vx表示车轮中心的前进速度;Vy表示车轮中心的侧向滑移速度;Vs表示相对滑移速度;μ0表示静摩擦系数取0.8;V0表示速度常数;Sx表示滑转率;Sy表示相对滑转率;Kx表示初始相对纵滑刚度;Ky表示相对侧滑刚度;Ey表示轮胎力特性参数。
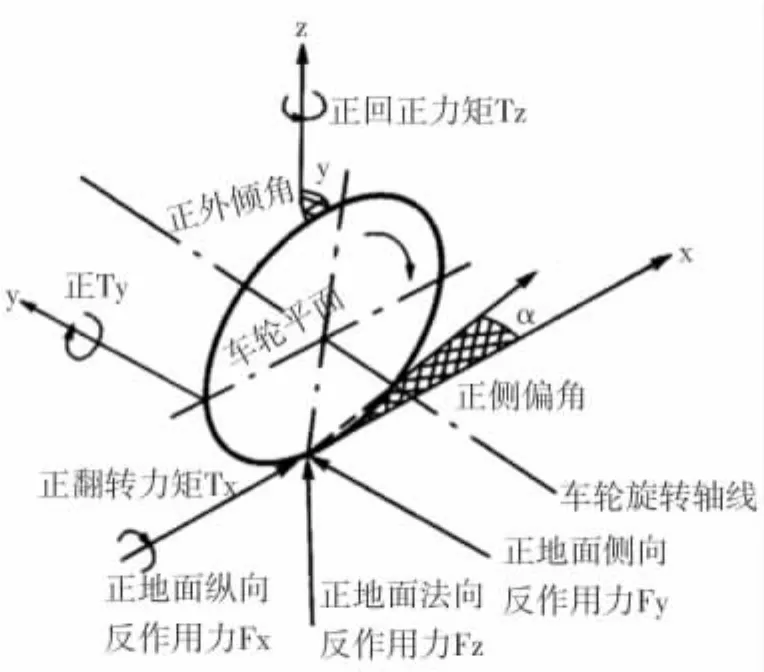
图2 轮胎受力坐标系
3 建模与仿真
根据上述建模分析,基于MATLAB软件建立电机仿真模型如图3,建立轮胎仿真模型如图4,电机各参数取值见表1。
在轮胎模型中给转向角加入阶跃信号,得到纵向力曲线和侧向力曲线如图5、6所示,由图中可以看出纵向力曲线逐步增大,最后趋于稳定,侧向力曲线由于轮胎的侧偏特性出现小幅度振荡,随后也趋于稳定。符合车辆从启动到稳定行驶后轮胎受力值趋于稳定的实际情况。
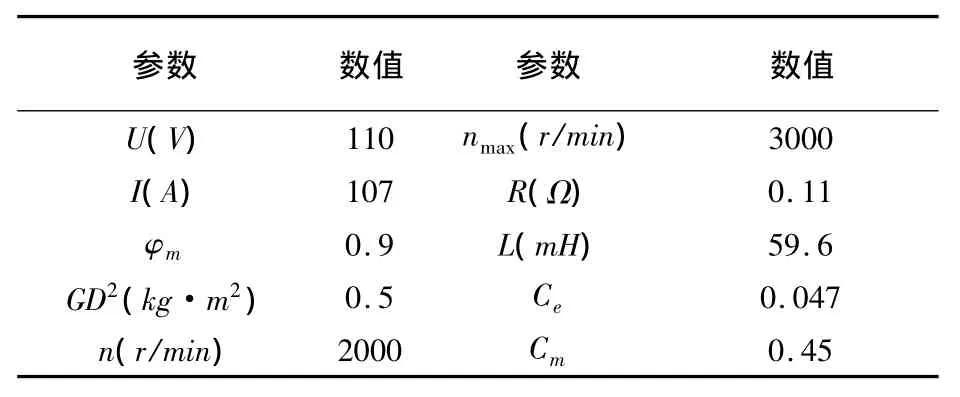
表1 电机参数取值
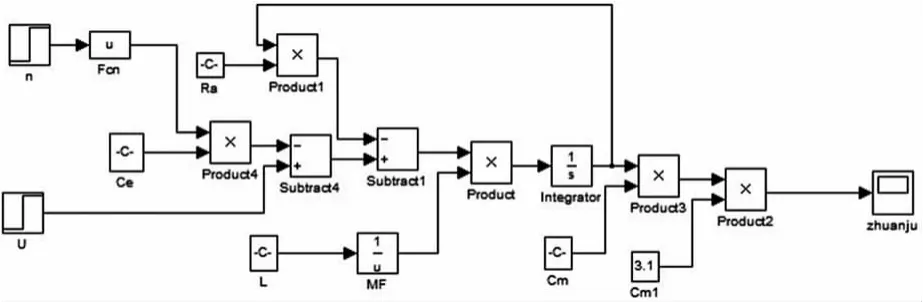
图3 电机模型
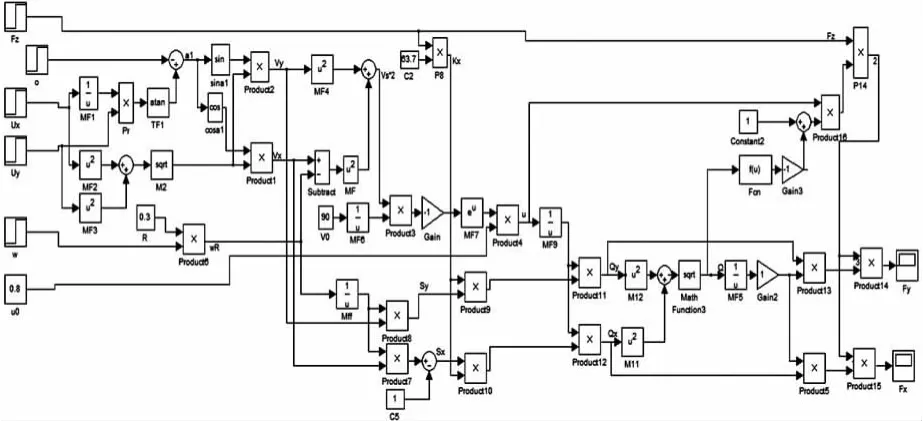
图4 轮胎模型
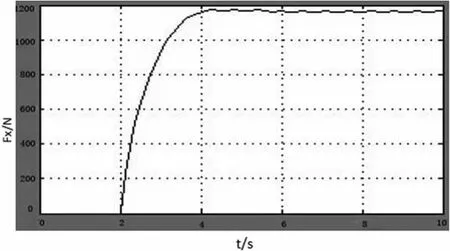
图5 纵向力曲线
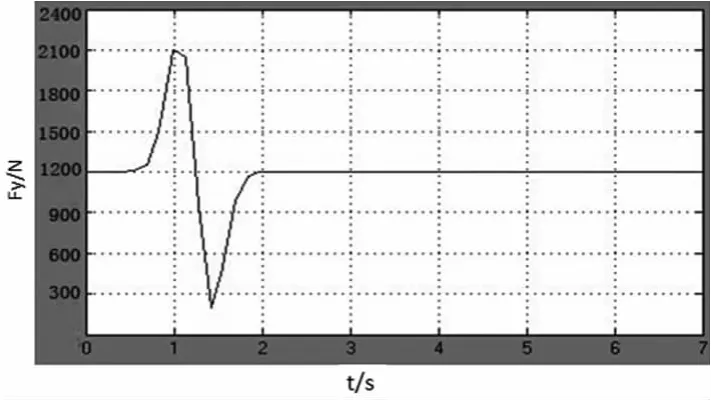
图6 侧向力曲线
在电机模型中给定一个阶跃输入得到转矩曲线如图7,从图中可以看出转矩能够迅速稳定,符合电动汽车转矩的理想输出,驱动系统具有较好的动态响应。
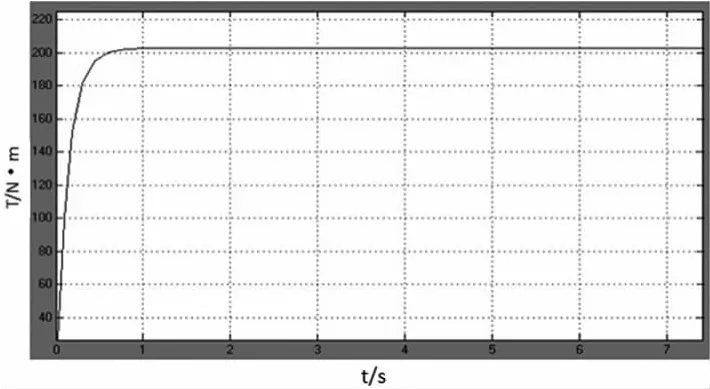
图7 电机转矩曲线
4 结 语
本文以轮式驱动电动汽车为研究对象,重点研究轮式驱动电动汽车的驱动系统,分析了电机和轮胎的数学模型,使用MATLAB软件进行动态仿真,根据仿真曲线,可以看出直流电机转矩输出符合汽车驱动系统的理想输出,轮胎模型的输出满足电动汽车运行要求。
[1]RICCARDO M,STEFANO S.Asymptotic sideslip angle and yaw rate decoupling control in four-wheel steering Vehicles[J].Vehicle System Dynamics,2008(9):999-1009.
[2]OSSAMA M,MASATO A.How the Four Wheels Should Share Forces in an Optimum Cooperative Chass is Control[J].Control Engineering Practice,2006(14):295-304.
[3]章昊秋.轮式驱动电动汽车驱动系统的研究[D].杭州:浙江大学,2007.
[4]来飞,黄超群.汽车操纵稳定性仿真用轮胎模型的研究[J].机械,2014,41(2):13-15.
[5]田顺,何海浪,赵建宁,等.车辆轮胎动力学仿真模型分析[J].汽车实用技术,2014(6):47-50.

