基于强度折减与正交试验的边坡支护优化设计

陈开良

(福州市城市地铁有限责任公司 福建福州 350001)

基于强度折减与正交试验的边坡支护优化设计

陈开良

(福州市城市地铁有限责任公司 福建福州 350001)

以漳州招银高速公路港尾互通(MK10+980 - MK11+253)的典型岩质边坡支护工程为背景，利用基于强度折减和正交试验的数值模拟方法，计算了25种不同锚索-框架梁支护方案下，该边坡的安全系数。进一步地，对上述各支护方案的工程量和造价进行了估算，同时利用专家问卷调查法构建了决策者对安全系数目标和工程造价目标的效用函数。最后利用效用并合理论，对锚索-框架梁支护方案进行了比选，认为17#方案为该岩质边坡的最优支护设计。

边坡稳定性；强度折减；正交试验；效用并合；优化设计

E-mail:40030688@qq.com

引 言

随着国民经济的迅速发展和基础设施建设的不断扩大，在矿山开采、交通运输、水利水电的建设中，越来越多地遇到高边坡的支护问题，其稳定性往往对整个工程的成败起着决定性作用[1]。另一方面锚索-框架梁的柔性支护技术已在工程实践中得到了广泛应用，并取得了巨大成功。使用锚索-框架梁技术可以充分发挥岩土体自身的抗剪强度，提高其自稳能力，有效控制岩土体及工程结构的变形[2,3]。然而实际工程中，锚索-框架梁的支护设计仍然停留在以围岩分级为基础的经验类比阶段，这有时会给边坡工程带来了一定隐患，而有时又会造成工程材料的极大浪费。因此，如何根据实际地质情况，确定最优锚固参数，对提高科学设计水平，节约工程成本具有重要意义[4]。

本文以漳州招银高速港尾互通(MK10+980 - MK11+253)的典型岩质边坡支护工程为背景，利用基于强度折减和正交试验的数值模拟方法，并考虑支护效果与工程造价之间的平衡，对锚索-框架梁支护体系进行优化设计。

1 工程背景

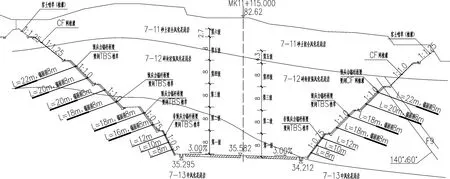
图1 路堑式边坡MK11+115断面设计图(单位：m)

漳州招银高速公路(MK10+980 ～ MK11+253)自西向东斜穿过一段东北-西南走向的山脊，在线路两侧形成了路堑式边坡。根据地勘资料和设计资料[5,6]，该段路堑式边坡采用预应力锚索(杆)框梁进行支护，其典型设计断面如(图1)所示。以右侧边坡为例，其走向为96°(与线路平行)，倾向为6°，倾角为45°。该侧边坡内各地层描述如下：7-11砂土状全风化花岗岩，灰黄色，岩芯风化成砂土状，矿物完全风化，厚度约10m～14m；7-12碎块状强风化花岗岩，灰黄色，岩芯以碎块状为主，矿物部分风化，厚度约27m～33m；7-13中风化花岗岩，斑杂色，岩芯破碎，节理裂隙发育，块状构造。同时该侧边坡内赋存一条F9断裂带，其走向为50°，倾向为140°，倾角为60°，长约1200m，厚约3～5m。

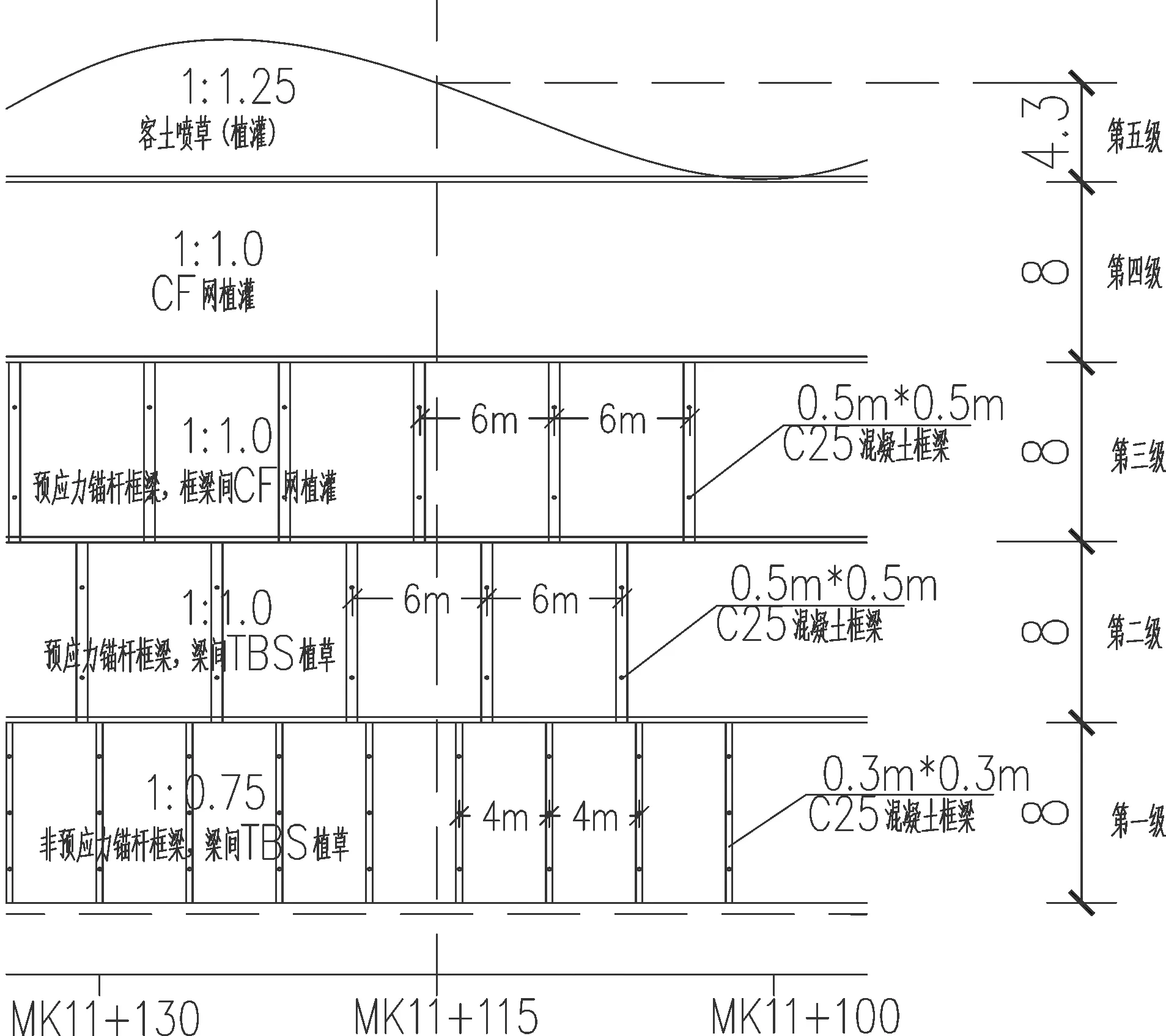
图2 右侧边坡立面设计图(单位：m)

右侧边坡设计为五级放坡，各级放坡之间的平台宽度均为2m，第五级坡高为4.3m，其余各级坡高均为8m。在第二级、第三级放坡中各打入两排预应力锚索，打入角度为20°，打设长度分别为22m、20m、18m和18m，锚固段均为8m，纵向间距均为6m，锚索抗拉强度均为1000kN，施加预加力为350kN，并在坡面上施做截面为0.5m*0.5m的C25混凝土框梁，连结两排锚索。在第一级放坡中打入三排非预应力锚杆，打入角度均为20°，打设长度分别为12m，10m和8m，并在坡面上施做截面为0.3m*0.3m的C25混凝土框梁，连结三排锚杆。该边坡的立面设计如(图2)所示。

2 基于有限元强度折减的稳定安全系数

根据以上断面设计和立面设计，在FLAC3D平台上建立三维数值模型，如(图3)所示。该模型包括5840个实体单元，7344个实体节点，271个结构单元，302个结构节点。模型x轴为水平横向，总长度为100m；y轴为线路纵向，厚度为20m；z轴为边坡高度方向，总高度为50m。参考地勘资料[5]和设计资料[6]，数值模型中所用到的各岩层物理力学参数取值详见(表1)，各支护结构的物理力学参数取值详见(表2)。

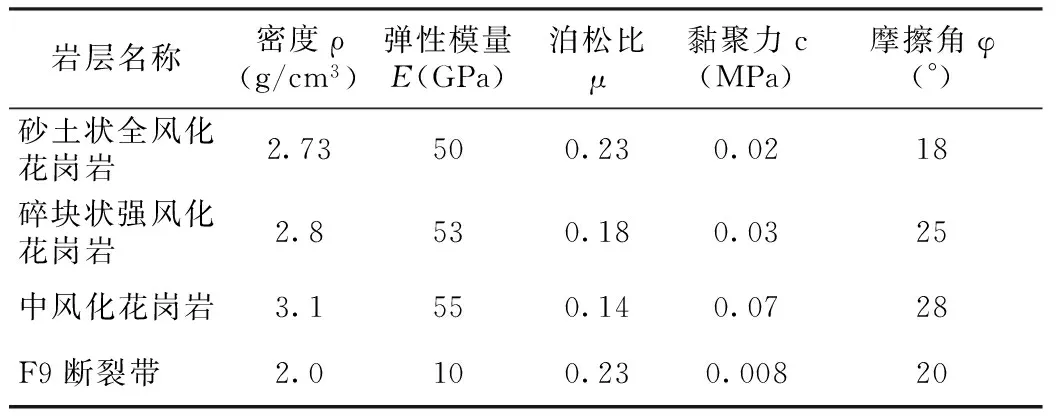
表1 各岩土层的物理力学参数

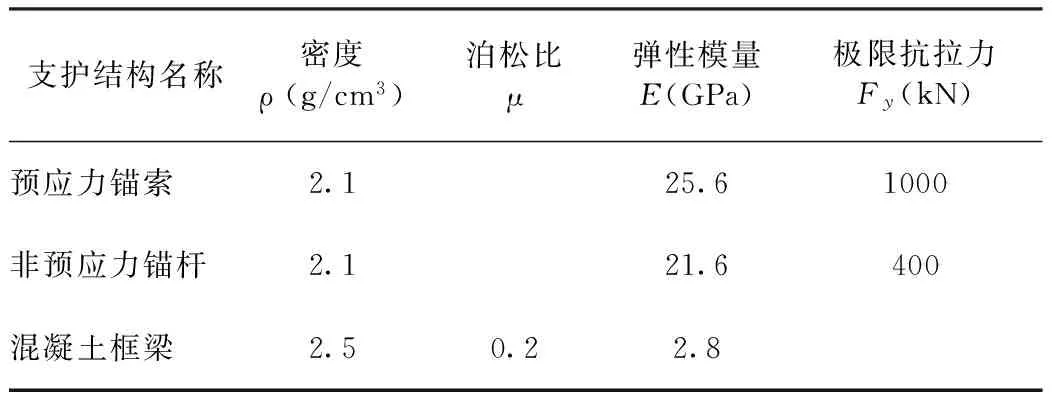
表2 各支护结构的物理力学参数

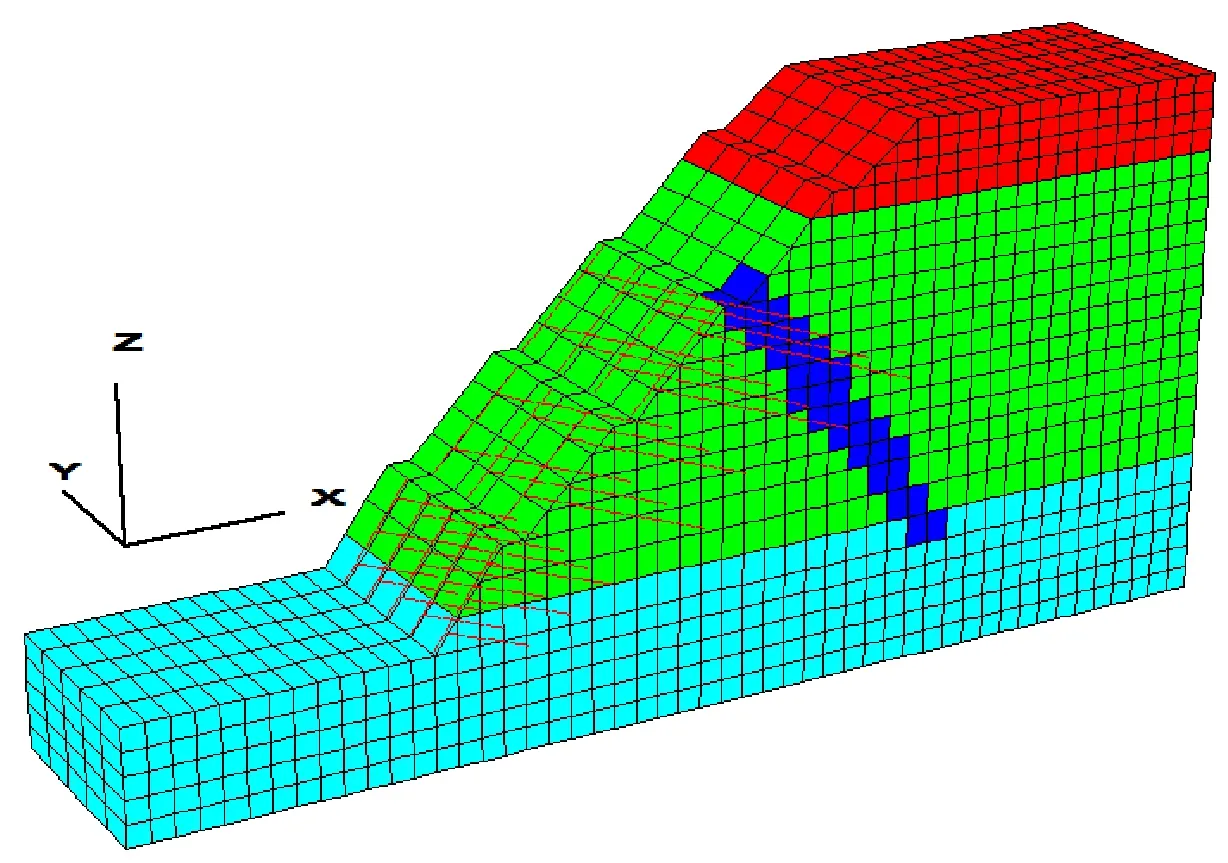
图3 右侧边坡的三维数值模型

在FLAC3D数值平台上，基于强度折减法来求解边坡稳定的安全系数，其定义为：通过对岩土体抗剪强度进行折减，使边坡达到临界破坏状态，此时岩土体的实际抗剪强度与折减后剪切强度比值即为边坡稳定安全系数Fs，如式(1)所示[7,8]。该安全系数具有强度储备的物理意义，在工程界得到广泛认可。

在FLAC3D数值平台中，对上述锚框支护边坡的三维数值模型进行反复试算，得到其稳定安全系数为1.514。另外为了说明锚框支护的效果，对无支护边坡也进行了基于强度折减的有限元数值模拟，得到其稳定安全系数为1.275。按相关规范要求[9]，对一级边坡其安全系数应大于1.35，故该边坡需采用必要的支护加固，以下对该边坡的锚框支护优化设计展开详细论述。

3 基于正交试验的支护效果对比

3.1 正交试验因素与水平设定

如上节所述，锚框支护的效果直接体现为边坡稳定安全系数的增加，但影响支护效果的因素很多，既有几何参数又有物理力学参数，要进行全面因素分析是很困难的。根据前人研究[10]，结合本工程实际情况，从支护优化设计的角度，选取锚索打入倾角，锚索长度，锚索纵向间距和锚索预应力等四个主要因素进行研究(非预应力锚杆不作为研究对象)。

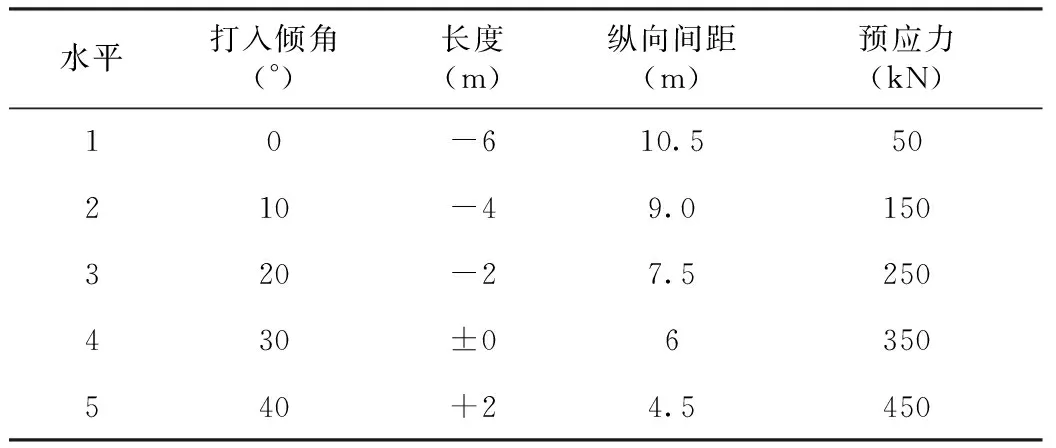
表3 四因素及五水平的设定

对以上四因素各选取五个水平，详见(表3)。其中水平4为原设计；水平3、水平2和水平1分别为在原设计基础上，倾角减小10°、20°和30°，锚索自由段长度减小2m、4m和6m，预应力减小100kN、200kN和300kN；水平5为在原设计基础上，倾角增加10°，锚索自由段长度增加2m，预应力增加100kN。

3.2 正交试验方案与试验结果

假设各因素间无交互作用，按照表3设定的四因素五水平，选用L25(56)的标准正交试验方案，详见(表4)。对此25种不同边坡锚框支护方案，进行了基于强度折减的有限元数值模拟，得到其安全系数如(表4)所示。

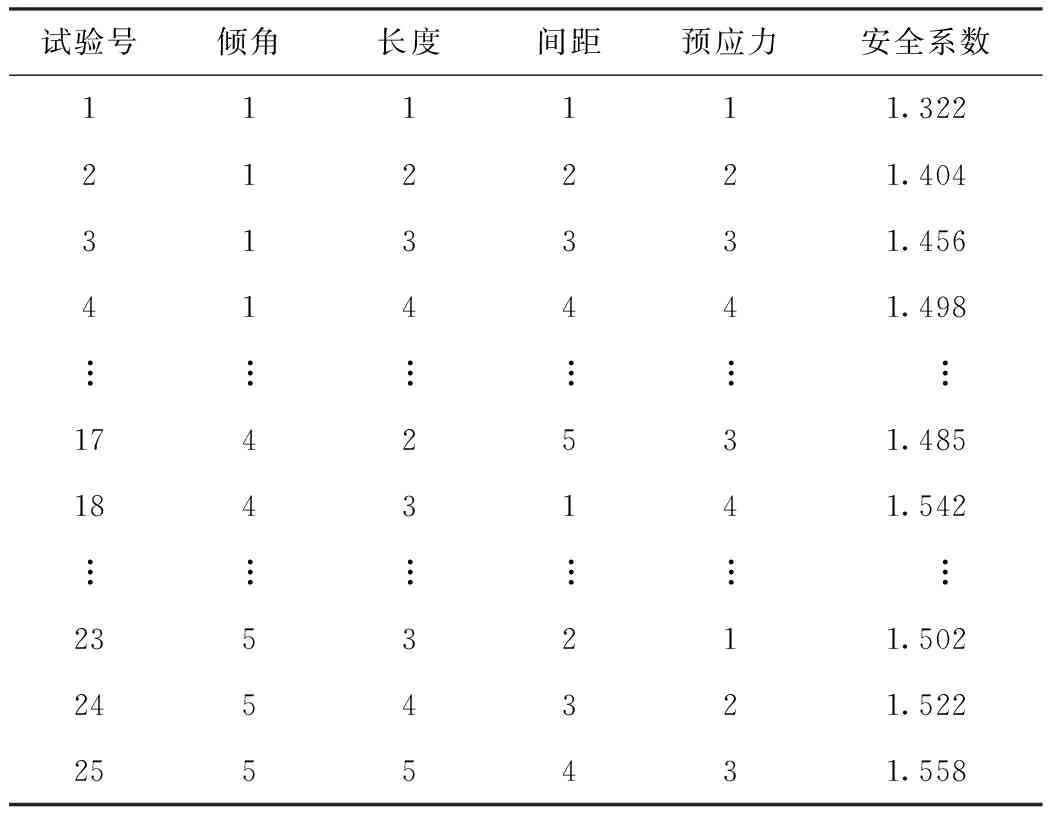
表4 正交试验方案及试验结果

3.3 极差分析与方差分析

对以上正交试验结果进行极差分析和方差分析，详见(表5)。从各因素的极差和F值中可知，各设计因素对边坡稳定性的影响，由大到小分别为：锚索长度、锚索预应力、锚索纵向间距和锚索打入角度。若设定置信水平α=0.1，则F临界值为2.33，因此各设计因素对边坡稳定性的影响均无法称之为显著。

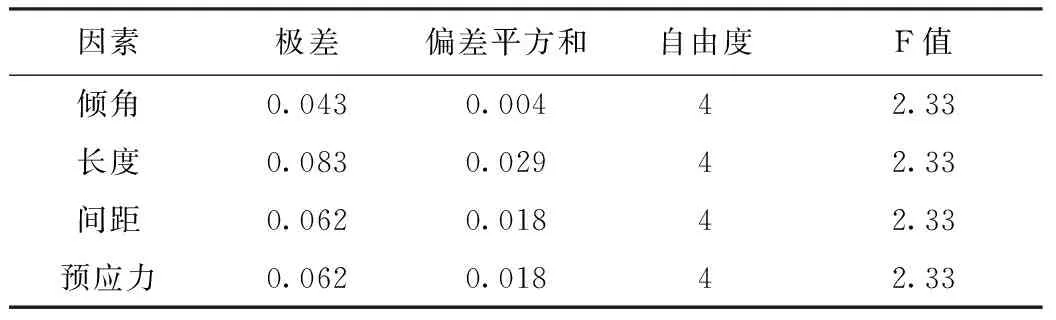
表5 正交试验结果的极差分析与方差分析

4 考虑支护效果与工程造价的优化设计

4.1 工程量与工程造价

根据公路工程预算定额[11]，各支护方案的工程量如(表6)所示。其中脚手架的工程量是按照边坡的表面积进行计算，地梁、锚座混凝土、预应力锚索的工程量是依据不同支护方案分别计算。同时公路工程预算定额中也给出了各分项工程的基价，进而可以确定工程造价，详见(表6)所示。

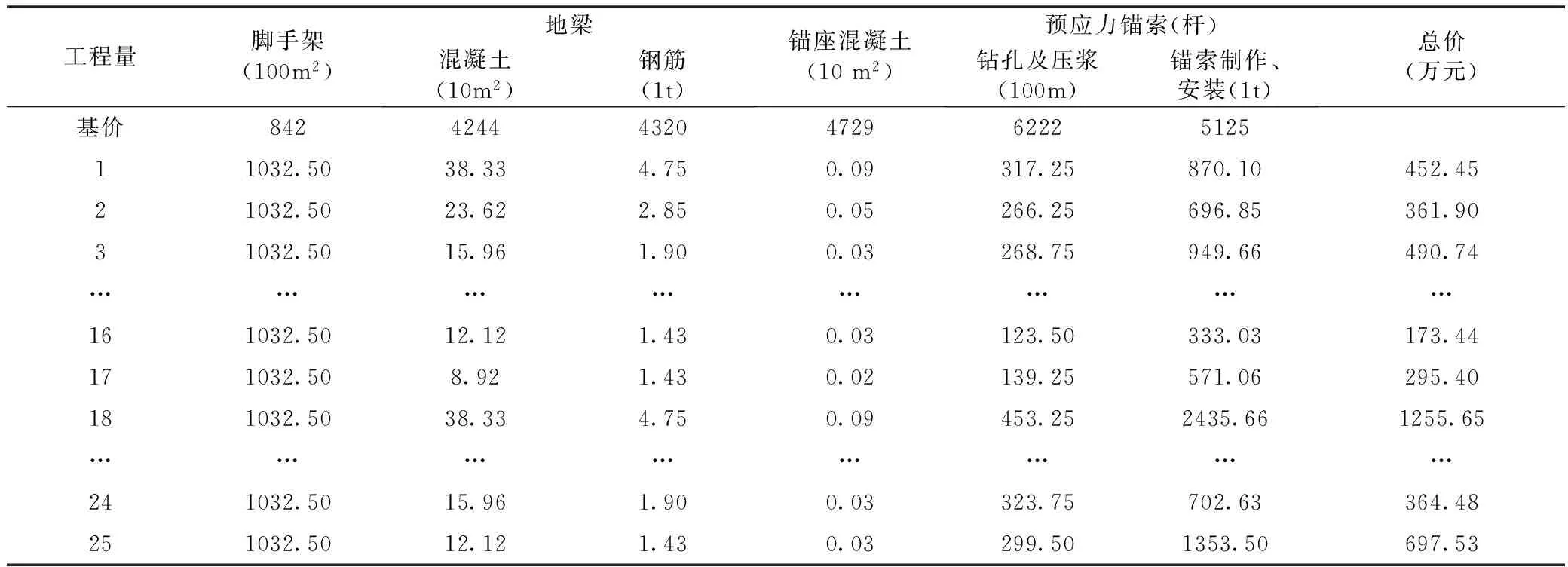
表6 各支护方案的工程量与工程总价

4.2 方案比选

从以上25种支护方案中比选出一种最优方案，是典型的多目标决策问题。它具有两个显著特点：一是目标间的不可公度性，二是目标间的矛盾性。因此需引入效用并合理论，才能对边坡支护优化做出合理决策。决策者对不同类型目标的期望损益都有不同的效用函数，该函数一般通过德尔菲咨询法(专家问卷调查法)来构建。最后将对不同决策目标的效用值通过某种规则并合起来(常用的并合规则有距离规则、代换规则、加法规则、乘法规则)，最终以并合效用值作为决策依据[12]。

首先应构建决策者对不同类型目标的效用函数。例如对于稳定安全系数，假定对最大安全系数(1.558)的效用值为1，对最小安全系数(1.322)的效用值为0，通过对8位决策者(包括建设方的3位专家、设计方的2位专家和施工方的3位专家)的多轮问卷调查，得到决策者关于安全系数的效用值散点图，并拟合成光滑的效用函数曲线如(图4)所示。同理对于工程造价，也通过上述方法拟合出效用函数曲线，如(图5)所示。

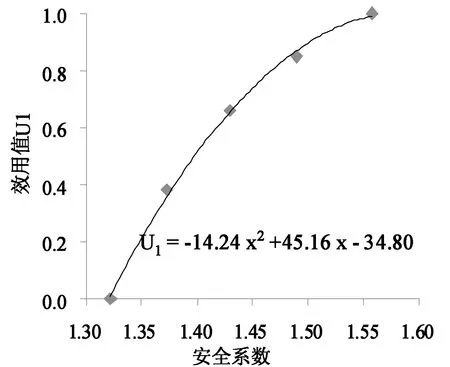
图4 关于稳定安全系数的效用函数

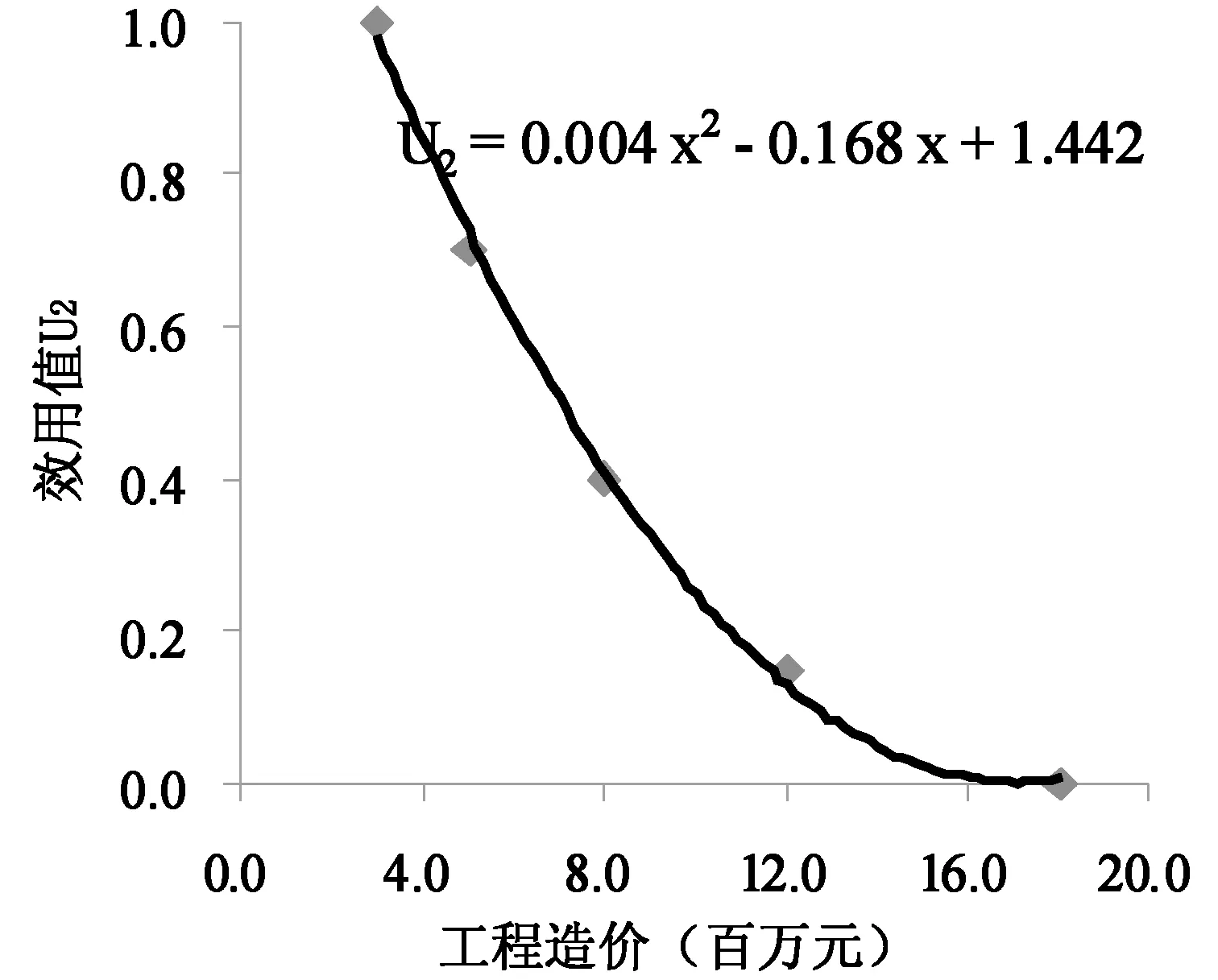
图5 关于工程造价的效用函数

将以上25种支护方案的安全系数和工程造价，分别代入其效用函数，求得其效用U1和U2，列于(表6)。然后利用距离并合规则(如式2所示)，计算各方案的并合效用值，也列于(表6)。

(2)

由该表可知，支护方案17#的并合效用值最大，所以建议以此作为该边坡锚索-框架梁支护的最优设计方案。

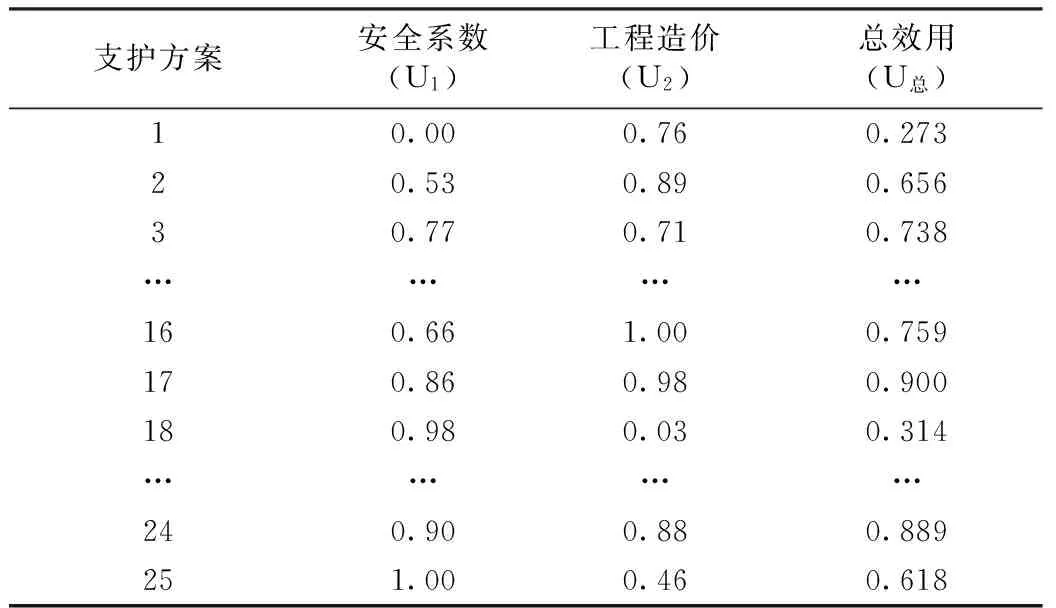
表6 各支护方案的效用比选

5 结论

以漳州招银高速公路港尾互通(MK10+980 - MK11+253)的典型岩质边坡支护工程为背景，利用基于强度折减和正交试验的数值模拟方法，计算了25种不同锚索-框架梁支护方案下，该边坡的安全系数。由极差分析和方差分析可知，锚索-框架梁支护中各设计因素对边坡稳定性的影响，由大到小分别为：锚索长度、锚索预应力、锚索纵向间距和锚索打入角度。

进一步地，根据公路工程预算定额，对上述各支护方案的工程量和造价进行了估算，同时利用专家问卷调查法，构建了决策者对安全系数目标和工程造价目标的效用函数。最后利用效用并合理论，对锚索-框架梁支护方案进行了比选，确认17#方案为该岩质边坡的最优支护设计。

[1]陈祖煜. 土质边坡稳定分析[M]. 北京: 中国水利水电出版社, 2003.

[2]吕庆, 孙红月, 尚岳全, 朱晗迓. 破碎岩质边坡预应力锚固机制数值模拟研究[J]. 岩石力学与工程学报. 2006, 25(9): 1848-1856.

[3]刘涌江, 杨静. 预应力锚索加固花岗岩类土质高边坡的现场测试研究[J]. 岩石力学与工程学报. 2011, (s1): 2924-2930.

[4]陈尤, 韦秉旭, 唐辉湘. 基于FLAC3D的岩质边坡锚杆优化设计. 中外公路. 2011:85-9.

[5]福建省交通规划设计院. 漳州招银高速公路(含海平支线)A3合同段地质评价.

[6]福建省交通规划设计院. 漳州招银高速公路(含海平支线)A3合同段设计资料.

[7]郑宏, 田斌, 刘德富等. 关于有限元边坡稳定性分析中安全系数的定义问题[J]. 岩石力学与工程学报. 2005(13): 2225-2230.

[8]胡松山, 童申家, 刘斌清等. 基于非均质边坡强度折减法的三维桥基边坡稳定性分析[J]. 岩土力学. 2014(S2): 653-661

[9]GB 50330-2013建筑边坡工程技术规范[S]. 北京:中国建筑工业出版社. 2013.

[10]张良发. 锚杆参数优化在开挖边坡加固中的应用研究. 资源环境与工程. 2011:248-51.

[11]中国人民共和国交通部. JTG/T B06-02-2007 公路工程预算定额. 2007.

[12]陶长琪. 决策理论与方法: 中国人民大学出版社; 2010.

Optimal Design of Slope Support Based on Strength Reduction Method and Orthogonal Test Method

CHENKailiang

(Fuzhou Urban Metro Co. Ltd., Fuzhou 350001)

Considering the rock slope support project in Gangwei Interchange of Zhaoyin Expressway (MK10+980 - MK11+253), using the numerical simulations based on strength reduction method and orthogonal test method, the safety factors of rock slope under 25 support schemes are calculated. Furthermore, the engineering quantity and the project cost for each support scheme are estimated. Meanwhile, the utility functions for both safety factor and project cost are constructed through expert questionnaire method. Then using the utility combination, the 17# support scheme is considered as the optimal design for the rock slope support project.

Slope stability; Strength reduction method; Orthogonal test method; Utility combination; Optimal design

陈开良(1982.10- )，男，工程师。

2015-03-05

TU4

A

1004-6135(2015)04-0066-05