精密直驱龙门系统的交叉耦合互补滑模控制

赵希梅 赵久威

(沈阳工业大学电气工程学院 沈阳 110870)



精密直驱龙门系统的交叉耦合互补滑模控制

赵希梅 赵久威

(沈阳工业大学电气工程学院 沈阳 110870)

针对龙门定位平台上双直线电动机伺服系统的位置精确同步控制问题，提出一种基于交叉耦合控制(Cross-Coupled Control，CCC)与互补滑模控制(Complementary Sliding Mode Control，CSMC)相结合的控制方案。考虑到永磁直线同步电动机(Permanent Magnet Linear Synchronous Motor，PMLSM)易受系统存在的端部效应、参数变化、外部扰动及非线性摩擦等不确定性因素的影响，建立含有不确定性因素的直线伺服系统的动态模型。为了使系统实现高精度强鲁棒性的位置跟踪性能，设计基于CCC和CSMC的双直线电动机伺服系统。利用CSMC对系统不确定性因素不敏感和抖振小的优点，来保证双直线电动机伺服系统中单轴的位置跟踪精度；并将CCC引入到双直线电动机伺服系统中，消除了双电动机之间存在的耦合，进而减小了系统的位置同步误差。系统实验结果表明，该控制方法具有快速的跟踪性和较强的鲁棒性，能够满足高精度强鲁棒性的实际加工生产需求。

双直线电动机伺服系统 交叉耦合控制 互补滑模控制 同步控制

0 引言

目前，高精度龙门定位平台已广泛用于工业机械加工中，如微电子学、精密计量学、电路装配、印刷电路板制造、平台薄板制造和检查等自动化生产过程[1]。在龙门定位平台中，采用两台PMLSM驱动龙门定位平台运动。尽管龙门定位平台两立柱具有相同的驱动及执行机构，但在两立柱运动中，由于不平衡力的存在和各种外界扰动以及机械装置的参数变化，都会不可避免地在两台PMLSM之间产生同步误差。同步误差将影响工件的加工质量，甚至会触发过电流保护，导致整个加工过程终止。因此，在高精度制造加工应用中，对龙门定位平台的定位精度提出了更高要求。

过去CCC大量应用在数控机床加工和多轴运动控制领域中，以得到较高的轮廓加工精度[2-5]。文献[2]采用了基于差分进化算法的变参数CCC方法，弥补了单轴伺服跟踪误差补偿轮廓误差效果不理想的缺点，进而提高了曲轴非圆磨削的加工精度。文献[3]提出了一种NURBS插补器CCC，解决了数控机床各联动轴动态性能不一致所导致的轮廓误差较大的问题。

众所周知，滑模控制的优点在于一旦系统到达且保持在滑模面上运动时，整个控制系统对参数变化和外部扰动变得不敏感[6-8]。滑模控制通常利用较大的切换增益来保证系统的鲁棒性，但这种切换控制往往会引起较大的抖振，抖振会使系统出现高频振荡，导致电路中高热量损失和机械运动高磨损[9，10]。为了削弱抖振，CSMC的切换控制率选用饱和函数来代替传统的切换函数，且CSMC采用两个滑模面相结合的设计，不仅可提高位置跟踪精度，还能提高系统的动态响应能力[11，12]。

为了解决精密直驱龙门定位平台的双直线电动机伺服系统的同步控制问题，本文提出了基于CCC和CSMC相结合的控制方案。CSMC很好地解决了直线伺服系统存在不确定性的问题，抖振现象也得到明显削弱，提高了单轴系统的位置跟踪精度。引入CCC消除了两台直线电动机之间的耦合关系，从而减小了系统的位置同步误差。最后通过实验结果验证了所提出的控制方法是有效可行的。

1 双直线电动机伺服系统数学模型

本文的龙门定位平台所采用的双直线电动机伺服系统由两台参数完全相同的PMLSM组成。采用磁场定向控制，那么定子电流矢量和永磁体磁场在空间上正交[13]，电磁推力Fei可简化为

Fei=Kfiiqi

(1)

Kfi=3πnpiλPMi/(2τi)

(2)

式中，Kfi为电磁推力常数；iqi为推力电流；λPMi为永磁体磁通(磁链)；npi为初级磁极对数；τi为极距；下标i=1或2，表示双直线电动机伺服系统的两个平行轴。

根据式(1)的电磁推力，PMLSM机械运动方程可表示为

(3)

式中，vi为动子速度；Mi为动子总质量；Bi为黏滞摩擦系数；Fi为扰动，包括电动机端部效应、参数变化、系统外界扰动及非线性摩擦力等。

假设不存在扰动Fi，根据式(1)和式(3)可得理想状态下的动态方程

(4)

式中，di(t)为动子位置；Ani=-Bi/Mi，Bni=Kfi/Mi；ui为控制器输出，ui=iq，即推力电流。考虑各种不确定性因素存在时，那么式(4)的动态方程变为

(5)

式中，Cni=-1/Mi；ΔAi、ΔBi和ΔCi为系统参数Mi和Bi所引起的不确定量；Hi为系统不确定性总和，表示为

(6)

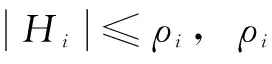
2 交叉耦合互补滑模控制系统设计

为了便于理解，给出在双直线伺服系统中，基于CCC和CSMC的单轴PMLSM伺服控制系统框图，如图1所示。

图1 基于CCC和CSMC的单轴PMLSM伺服控制系统框图Fig.1 Configuration of single axial PMLSM servo control system based on CCC and CSMC

在双直线电动机伺服系统中，同时考虑单轴位置跟踪误差和两轴间的位置同步误差。首先定义位置跟踪误差为

ei=dm-di

(7)

式中，dm为位置输入给定。同步误差定义为

ε1=e1-e2，ε2=e2-e1

(8)

式中，ε1和ε2分别表示两台PMLSM的同步误差。如果式(8)中同步误差为零，那么双直线电动机即为同步运行。将式(8)改写为矩阵形式，即

(9)

为了确保跟踪误差和同步误差同时收敛到零，将两误差相结合，定义为混合误差，表示为

(10)

式中，Eh=[eh1eh2]T，eh1和eh2分别表示双直线电动机的混合误差；β为两直线电动机耦合系数。将式(9)代入式(10)可得

Eh=(I+βT)E

(11)

双直线电动机伺服系统交叉耦合互补滑模控制框图如图2所示。为了满足控制需要，广义滑模面Si设计为

(12)

图2 双直线电动机伺服系统交叉耦合互补滑模控制框图Fig.2 Configuration of cross-coupled CSMC for dual linear motors servo system

式中λi是一个正常数。对式(12)求导，并结合式(5)可得

(13)

设计第2个滑模面，即互补滑模面SCi为

(14)

由于一台PMLSM控制系统中的广义滑模面和互补滑模面选择了相同的λi，那么Si和SCi的关系可表示为

(15)

根据式(12)～式(14)，得到交叉耦合互补滑模控制率ui为

ui=ueqi+uhiti

(16)

(17)

(18)

式中，ueqi为等效控制率；uhiti为切换控制率；sat(·)为饱和函数；Φi为边界层厚度。饱和函数具体表示为

(19)

为了从理论上分析验证基于CCC和CSMC相结合的控制方案对跟踪误差和同步误差的收敛性，选择李雅普诺夫函数为

(20)

对式(20)求导，并结合式(13)、式(15)～式(18)，可得

(21)

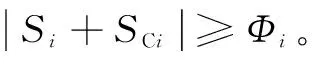
3 系统实验

实验中选择型号为TMS320 LF2812A的DSP作为控制算法核心，对交叉耦合互补滑模控制双直线电动机伺服系统进行实验研究，其中主要包括两台参数相同的PMLSM、PC+DSP运算控制单元、IPM主回路功率变换单元、动子电流检测单元和直线光栅尺位置检测单元等，其硬件结构如图3所示。

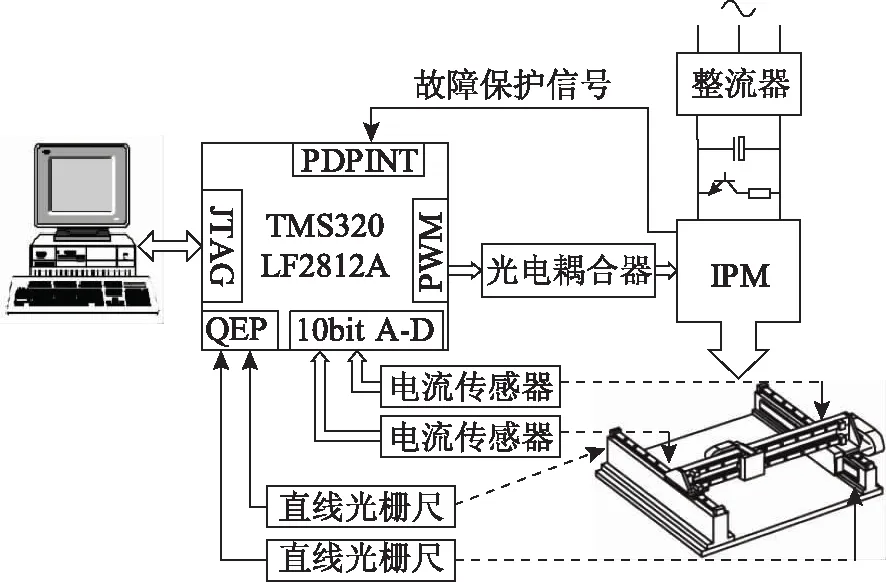
图3 DSP控制系统硬件结构图Fig.3 Block diagram of the DSP-based control system

双直线电动机中的PMLSM参数选择如下：Kfi=50.7 N/A，Mi=16.4 kg，Bi=8.0 N·s/m，Ri=2.1 Ω，Ψfi=0.09 Wb，τi=32 mm，β=0.3。为了使系统达到最优的控制效果，针对不同输入指令，经过反复调试参数，互补滑模控制器的参数最终选择：λi=87，ρi=8，Φi=0.000 4。

图4为输入幅值1 mm的阶跃输入，且在2 s和6 s时分别对两轴施加50 N扰动时，双直线电动机伺服系统的跟踪误差和同步误差曲线图。从图中可看出，输入指令后，系统跟踪指令迅速，在突加扰动时，最大跟踪误差为13 μm，最大同步误差为20 μm，且均能快速恢复到稳定状态，系统鲁棒性较强。

图4 阶跃输入实验结果Fig.4 Experimental results of step input

图5为输入幅值4 mm、频率0.2 Hz的正弦曲线时，双直线电动机伺服系统的跟踪误差和同步误差曲线图。图6为输入幅值6 mm、频率0.6 Hz的正弦曲线时，双直线电动机伺服系统的跟踪误差和同步误差曲线图。从图5、图6中可看出，4 mm/0.2 Hz正弦输入的跟踪误差基本稳定在4 μm左右，系统响应初期同步误差约±10 μm，在±5 μm间趋于稳定；6 mm/0.6 Hz正弦输入的跟踪误差基本稳定在7 μm左右，系统响应初期同步误差在-10～15 μm范围内，在±6.5 μm间趋于稳定。实验结果证明，当存在端部效应等不确定性时，龙门定位系统对不同输入均具有较高的定位精度。

图5 4 mm/0.2 Hz正弦参考轨迹实验结果Fig.5 Experimental results of 4 mm/0.2 Hz sinusoidal reference trajectory

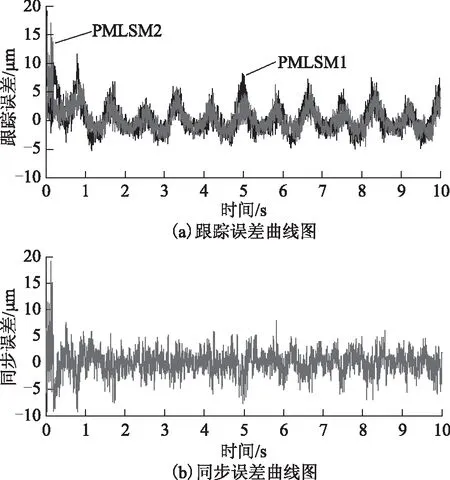
图6 6 mm/0.6 Hz正弦参考轨迹实验结果Fig.6 Experimental results of 6 mm/0.6 Hz sinusoidal reference trajectory

4 结论

本文针对龙门定位平台中双直线电动机位置同步控制问题，考虑到直线电动机不确定性因素和双直线电动机存在的耦合关系，提出了一种交叉耦合互补滑模控制策略。首先推导了直线电动机含有不确定性的动态方程，并利用CCC将单轴跟踪误差和同步误差结合为混合误差，这样保证了单轴跟踪误差和同步误差可同时收敛到零。然后将计算后的混合误差作为各轴的控制输入，各轴控制器选用互补滑模控制器。从理论上分析证明了基于CCC和CSMC的双直线伺服系统的稳定性和误差收敛性。实验结果表明，通过采用CCC和CSMC结合的控制方法，当存在扰动的阶跃输入时，最大跟踪误差为13 μm，最大同步误差为20 μm；不同正弦输入下，系统单轴跟踪误差和同步误差分别保证在15 μm和7 μm以内。验证了不同情况下龙门定位平台的双直线电动机伺服系统具有较高的动态性能和强鲁棒性，足以应对实际加工需求。

[1] Tan K K，Lee T H，Huang S.Precision Motion Control[M].2nd ed.Berlin，Germany：Springer-Verlag，2008.

[2] 李静，何永义，方明伦，等.曲轴非圆磨削中基于差分进化算法的变参数交叉耦合轮廓控制[J].机械工程学报，2011，47(9)：139-145. Li Jing，He Yongyi，Fang Minglun，et al.Cross-coupled contour control with variable parameters based on differential evolution algorithm in crankshaft non-circular grinding[J].Journal of Mechanical Engineering，2011，47(9)：139-145.

[3] 赵国勇，赵福令，徐志祥.一种基于NURBS插补器的高精度交叉耦合控制方法[J].大连理工大学学报，2008，48(2)：210-214. Zhao Guoyong，Zhao Fuling，Xu Zhixiang.High-precision cross-coupled control approach based on NURBS curve interpolator[J].Journal of Dalian University of Technology，2008，48(2)：210-214.

[4] Rodriguez A，Nijmeijer H.Mutual synchronization of robots via estimated state feedback：a cooperative approach[J].IEEE Transactions on Control System Technology，2004，12(4)：542-554.

[5] Yan M T，Lee M H，Yen P L.Theory and application of a combined self-tuning adaptive control and cross coupling control in a retrofit milling machine[J].Mechatronics，2005，15(2)：193-211.

[6] 茅靖峰，吴爱华，吴国庆，等.基于扩张状态观测的永磁直驱风力发电系统MPPT自适应滑模控制[J].电力系统保护与控制，2014，42(18)：58-65. Mao Jingfeng，Wu Aihua，Wu Guoqing，et al.Adaptive sliding mode MPPT control for PMSG-based wind energy conversion systems based on extended state observer[J].Power System Protection and Control，2014，42(18)：58-65.

[7] 史婷娜，刘立志，王慧敏，等.矩阵变换器-永磁同步电机驱动系统滑模变结构控制[J].电工技术学报，2010，25(12)：54-60. Shi Tingna，Liu Lizhi，Wang Huimin，et al.Sliding mode variable structure control for matrix converter fed permanent magnet synchronous motor drive system[J].Transactions of China Electrotechnical Society，2010，25(12)：54-60.

[8] Hacioglu Y，Arslan Y Z，Yagiz N.MIMO fuzzy sliding mode controlled dual arm robot in load transportation[J].Journal of the Franklin Institute，2011，348(8)：1886-1902.

[9] Matas J，de Vicuna L G，Miret J.Feedback linearization of a single-phase active power filter via sliding mode control[J].IEEE Transaction on Power Electronics，2008，23(1)：116-125.

[10]Cao J B，Cao B G.Fuzzy-logic-based sliding-mode controller design for position sensorless electric vehicle[J].IEEE Transaction on Power Electronics，2009，24(10)：2368-2378.

[11]Orlowska-Kowalska T，Dybkowski M，Szabat K.Adaptive sliding mode neuro-fuzzy control of the two-mass induction motor drive without mechanical sensors[J].IEEE Transactions on Industrial Electronics，2010，57(2)：553-564.

[12]Garcia-Gabin W，Zambrano D，Camacho E F.Sliding mode predictive control of a solar air conditioning plant[J].Control Engineering Practice，2009，17(6)：652-663.

[13]陆华才，江明，郭兴众，等.永磁直线同步电机推力波动约束[J].电工技术学报，2012，27(3)：128-132. Lu Huacai，Jiang Ming，Guo Xingzhong，et al.Thrust ripple suppression for permanent magnet linear synchronous motor[J].Transactions of China Electrotechnical Society，2012，27(3)：128-132.

Cross-Coupled Complementary Sliding Mode Control for Precision Direct-Drive Gantry System

ZhaoXimeiZhaoJiuwei

(School of Electrical Engineering Shenyang University of Technology Shenyang 110870 China)

A control method combining cross-coupled control (CCC) and complementary sliding mode control (CSMC) is proposed for precision position synchronization control problems of dual linear motors servo system in a gantry position stage.Considering that the permanent magnet linear synchronous motor (PMLSM) is vulnerable to the influence of the uncertainties，such as inherent end effect，parameter variations，external disturbances and nonlinear friction and so on，the dynamic model of the linear servo system with uncertainties is established.Then，dual linear motors servo system based on CCC and CSMC is designed in order to make the system achieve accurate position tracking performance with high precision and strong robustness.The advantage of CSMC which is not sensitive to uncertainty factors and with small chattering is used for guaranteeing position tracking precision of the single axis in dual linear motors servo system.CCC is introduced into dual linear motors servo system to eliminate the coupling between the dual linear motors，thus the position synchronization error is reduced.Finally，some system experimental results are illustrated to show that the proposed control method has fast tracking performance and strong robustness.It can satisfy actual production requirements with high precision and strong robustness.

Dual linear motors servo system，cross-coupled control，complementary sliding mode control，synchronous control

国家自然科学基金(51175349)，辽宁省教育厅科学技术研究项目(L2013060)和沈阳市科技计划项目(F12-277-1-70)资助。

2014-12-07 改稿日期2015-04-03

TP273

赵希梅 女，1979年生，博士，副教授，研究方向为直线伺服、数控、鲁棒控制等。(通信作者)

赵久威 男，1991年生，硕士研究生，研究方向为直线伺服、智能控制等。