电网不平衡情况下并网逆变器多目标协调控制策略研究

阳同光 桂卫华

(1.湖南城市学院信息科学与工程学院 益阳 413000 2.中南大学信息科学与工程学院 长沙 410083)



电网不平衡情况下并网逆变器多目标协调控制策略研究

阳同光1，2桂卫华2

(1.湖南城市学院信息科学与工程学院 益阳 413000 2.中南大学信息科学与工程学院 长沙 410083)

在电网电压不平衡情况下，并网逆变器输出有功功率和电流将存在二次脉动和畸变。为了提高电网不平衡时并网逆变器并网电流质量，有效降低并网逆变器对电网的冲击，提出了一种基于神经网络的电网不平衡情况下并网逆变器多目标协调控制策略。该策略根据瞬时功率计算参考电流矢量，建立多控制目标的统一解析表达式，并利用ADALINE神经网络对参考电流矢量表达式系数进行优化。为了提高系统的抗干扰性能，采用增量式PI控制器进行电流控制，并利用RBF神经网络在线调整PI控制器参数。仿真和实验结果验证了所提方法的有效性和适用性。

电网不平衡 并网逆变器 多目标协调控制 神经网络

0 引言

近年来，随着光伏、风力发电等新能源技术的不断发展，有关绿色能源并网的相关技术成为研究热点。并网逆变器作为可再生能源发电、大规模储能系统的并网接口，其控制是实现电能高效安全应用的基础。电网不平衡是电力系统中最常见的故障之一，大功率单相负载的接入、单相负载在三相系统中的不均衡分配和单相负载用电的随机性等因素，都会造成电网三相电压不平衡[1]。当电网电压不平衡时，电网电压中将含有负序分量，由于基于平衡电网情况下的并网逆变器控制策略缺乏负序电压控制，导致并网逆变器并网电流失去单纯正弦特性[2]，谐波含量急剧增加[3]，并将在直流母线电压、有功和无功功率中产生不可控的二次脉动，严重时会引起系统性能急剧恶化[4]。此时，如果不调整基于电网电压平衡情况设计的控制策略，并网逆变器的输出性能将严重下降，电网不平衡进一步恶化并对并网负载产生很大影响。

近年来，不平衡电网状态下并网逆变器控制引起广大学者的重视，成为研究热点。文献[5]为解决电网电压跌落情况下并网逆变器输出功率波动的问题，在同步旋转坐标系下分别对正负序电流分量进行控制，即双矢量电流控制(Dual Vector Current Control，DVCC)。但当逆变器容量较高、不平衡电流较大时将导致直流侧电容电压产生脉动[6]，降低并网功率质量。此外，在静止坐标系下由于无需坐标变换便可实现电网不平衡下并网逆变器控制，得到越来越多的重视，但在静止坐标系下并网逆变器输出电流为正弦量，此时，采用传统PI控制器会存在稳态误差的问题[7]。为改进这种不足，文献[8，9]采用谐振控制器PR代替PI控制器，取得较好的控制效果。上述方法虽然是直接电流控制，但从本质上讲，这些控制算法都属于恒定输入功率调节，因此，如何根据给定功率计算电流参考矢量成为实现控制目标的关键。文献[10，11]采用虚拟导纳方法根据不同并网导则对并网逆变器提出5种有功功率和无功功率控制策略。文献[6-8]则根据电网不平衡情况下瞬时功率分别实现保持输出有功功率恒定、消除无功功率波动和消除负序电流3种控制目标。但这些控制方法都属于极端控制[12]，即只能满足其中一种控制目标，无法取得多个控制目标之间优化。基于此，文献[12-14]提出协调控制的方法，对5种控制策略采用统一的参考电流表达式，通过设置参数取得不同控制目标之间的平衡，使控制性能达到最优。

本文提出一种基于ADALINE神经网络的电网不平衡情况下并网逆变器的多控制目标的协调控制策略。该方法采用瞬时功率直接计算电流参考矢量，建立基于不同控制目标的统一电流参考矢量解析表达式，并利用ADALINE神经网络对表达式系数进行优化。电流控制采用增量式PI控制，并利用RBF神经网络PI控制器参数进行在线调整。

1 电网不平衡时并网逆变器数学模型

三相电压型并网逆变器主电路拓扑结构如图1所示。

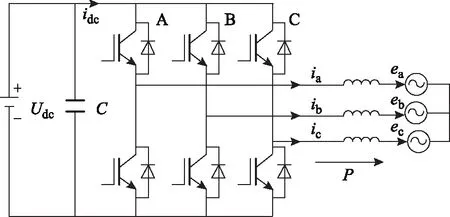
图1 并网逆变器主电路拓扑结构图Fig.1 Topology of the grid-connected inverter

图1中，ea、eb、ec分别为电网电压；ia、ib、ic分别为逆变器输出电流；Udc为直流侧电压；C为直流侧电容。

三相电网不平衡时，若只考虑基波，则电网电动势为[14]

(1)

(2)

根据图1，可得并网逆变系统的电压为

(3)

将式(2)代入式(3)可得到两个解耦的表达式

(4)

(5)

当三相电网不平衡时，并网逆变器网侧的复功率为

(6)

将式(2)代入式(6)，则瞬时有功功率和无功功率为

P(t)=P0+Pc2cos(2ωt)+Ps2sin(2ωt)

(7)

Q(t)=Q0+Qc2cos(2ωt)+Qs2sin(2ωt)

(8)

式中，P0、Q0为有功、无功功率平均值；Pc2、Ps2、Qc2、Qs2分别为二次有功、无功的正弦余弦峰值。

(9)

(10)

(11)

(12)

(13)

(14)

通过式(9)～式(14)，可以发现上述功率方程组有6个表达式，采用4个参考电流给定值无法同时控制6个功率值，因此，采用一个控制策略无法同时实现所有控制目标。

2 电网不平衡时并网逆变器控制策略

2.1 参考电流计算

根据式(9)～式(14)选取不同控制目标，可计算不同控制目标的参考电流矢量。3个不同控制目标下参考电流矢量表达式分别描述如下[9]。

1)控制目标1：负序电流为零，实现并网逆变器正弦电流并网，消除谐波电流。联立式(9)～式(12)可得

(15)

根据式(15)可求得正序电流参考矢量为

(16)

2)控制目标2：抑制直流电压脉动，保持并网有功功率恒定，消除有功功率二次脉动，即Pc2=Ps2=0。联立式(9)～式(12)可得到参考电流矢量为

(17)

3)控制目标3：在为电网提供无功支撑的情况下，保持无功功率恒定，即Qc2=Qs2=0。联立式(9)、式(12)～式(14)可求得参考电流矢量为

(18)

(19)

式中，0≤k≤1；0≤γ≤1。

通过分析式(19)发现，选取不同系数，将实现3个不同控制目标。当k=1、γ=1时，实现控制目标1；当k=0、γ=0时，实现控制目标2；当k=1、γ=0时，则实现控制目标3。参数γ主要和负序电流有关，当γ=1时，参考电流矢量不包含负序分量，但并网有功和无功功率存在较大波动；而γ=0时，能结合k值有效消除并网有功和无功功率的波动，实现恒功率并网，但并网电流谐波较大。

2.2 基于神经网络多目标协调控制设计

上述控制目标通常用有功功率脉动、无功功率脉动和总谐波(Total Harmonic Distortion，THD)3个控制指标衡量[12]。但3个控制目标互相冲突，一个控制目标性能改善往往导致另一个控制目标性能下降[12]。因此，有必要设计一种控制策略能够根据实际情况在多控制目标之间进行协调，通过对表达式系数k、γ进行优化，兼顾多个控制指标。

自适应线性神经元(AdaptiveLinearNeuron，ADALINE)是由美国Standford大学B.Widrow等[15]提出。ADALINE是一种多输入、单输出的具有自适应学习特性的单层线性神经元。由于其具有结构简单、易于实现的特点，被广泛用于谐波电流检测[16]和电机参数辨识[17]等。ADALINE自适应线性神经网络结构如图2所示。图2中，X1、X2、X3分别为神经网络输入，W1、W2、W3分别为神经网络权值，O为输出函数。

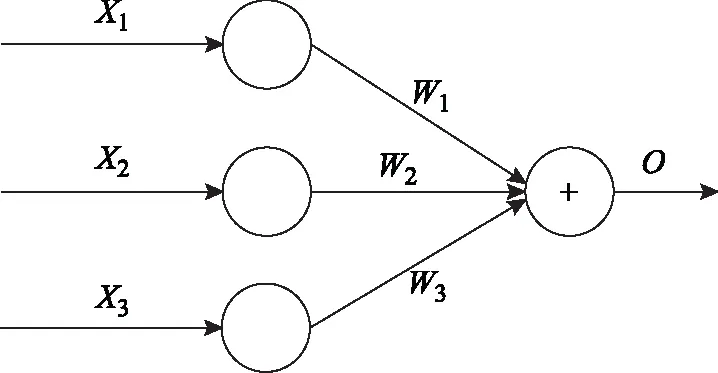
图2 神经网络单元结构Fig.2 Block diagram of neural network

为便于分析，式(19)可写为

(20)

式中

将式(20)转换为矩阵形式可得

(21)

Ii=Wi1X1+Wi2X2，i=1, 2, 3, 4

(22)

(23)

(24)

基于ADALINE神经网络的参考电流正负序分量和最优系数辨识单元结构如图3所示。辨识器由4个神经网络单元组成，分别辨识参考电流的4个分量和2个系数。

图3 基于神经网络参数辨识结构图Fig.3 Block diagram of parameter identification based on neural network

神经网络权值调整算法采用Wirdow-Hoff学习规则[15]。在采样点n时刻，令误差为

(25)

定义能量函数为

(26)

学习过程中神经网络权值变化可表示为

(27)

式中，i=1、2。则神经网络权值训练表达式为

(28)

式中，η为学习率；α为动量因子。

2.3 基于神经网络的PI控制器整定

并网逆变器控制器电流内环控制一般采用PI控制器[1-6]、PR控制器[8，9]。为进一步提高电网不平衡情况下并网逆变器控制性能，一些非线性控制方法也被用于并网逆变器内环电流控制，如无差拍控制[12]、滑模控制[18]、预测控制[19]和无源控制[20]等。本文选用增量式PI控制器，为提高其鲁棒性，利用RBF神经网络在线自适应调整控制器参数。

RBF神经网络结构如图4所示，其中中间层由径向基函数构成，输出为中间节点的线性函数，表示为被控对象的辨识信息。中间节点的基函数选取高斯函数

(29)

式中，X为n维输入矢量；cj=[cj1,cj2,…，cjn]T为基函数中间矢量；σj为j个基函数的基宽。

图4 RBF神经网络结构图Fig.4 Block diagram of RBF neural network

并网逆变器电流控制误差定义为式(26)，PI控制器的输入为

xe(1)=e(n)-e(n-1)

(30)

xe(2)=e(n)

(31)

增量式PI控制器的输出为

u(n)=u(n-1)+KPxe(1)+λKIxe(2)

(32)

式中，λ为积分度，0≤λ≤1；KP、KI分别为比例积分系数。

神经网络整定PI控制器的目标函数为

(33)

采用梯度下降法调整系数KP、KI为

(34)

(35)

设RBF神经网络的辨识误差和能量函数分别为

(36)

(37)

则采用梯度下降法可求得RBF神经网络权值调整为

(38)

(39)

σj(n)=σj(n-1)+ηΔσj+α[σj(n-1)-σj(n-2)]

(40)

(41)

cji(n)=cji(n-1)+ηΔcji+α[cji(n-1)-cji(n-2)]

(42)

(43)

式中，α为动量因子。

基于RBF神经网络自适应PI控制器结构如图5所示。

图5 神经网络动态整定PI控制器结构图Fig.5 Block diagram of turning PI by neural network

电网不平衡情况下并网逆变器控制系统结构如图6所示。采用二阶广义积分器(Second-OrderGenerali-zedIntegrator，SOGI)进行电压和电流的正负序分量提取，具体设计参见文献[21，22]，电网电压同步信号由锁相环PLL求取。电压正负序分量输入ADALINE神经网络，用于辨识参考电流矢量和参数优化，电流正负序分量与ADALINE神经网络辨识的参考电流矢量一起用于电流控制。电流控制采用增量式PI控制器，并通过RBF神经网络在线自适应调整PI控制器参数。

图6 并网逆变器控制器结构图Fig.6 Block diagram of the grid-connected inverter controller

3 仿真及结果分析

为验证电网不平衡情况下基于ADALINE神经网络控制策略的有效性，基于Matlab/Simulink建立并网逆变器系统模型进行仿真。系统主要技术参数如表1所示。

表1 仿真参数Tab.1 Simulation parameters

图7为电网电压A相在跌落20%的稳态情况下，k=1、γ=1时仿真结果图，电网电压在0.5 s时发生单相跌落，跌落后电流波形保持较好，但直流电容电压脉动较大，并网逆变器输送电网的有功功率和无功功率存在较大的波动，实现抑制负序电流的控制目标。图8为k=1、γ=0时仿真结果图，抑制并网逆变器输出无功功率波动，但存在较大的负序电流和有功功率波动，此时控制策略实现控制目标3。图9为k=0、γ=0时仿真结果图，由图9可知，发生电网跌落后，有功功率的脉动得到明显抑制，但无功功率脉动较为严重，而且并网电流存在较大的负序电流。综合图7～图9可以发现，3种控制策略都是极端控制，即只能满足某一个控制目标，无法在3个控制目标之间取得平衡，与前面理论分析比较吻合。

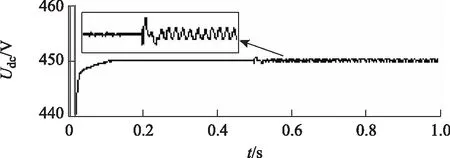
图7 参数k=1、γ=1时仿真结果图Fig.7 Simulation results with k=1 and γ=1

图8 参数k=1、γ=0时仿真结果图Fig.8 Simulation results with k=1 and γ=0

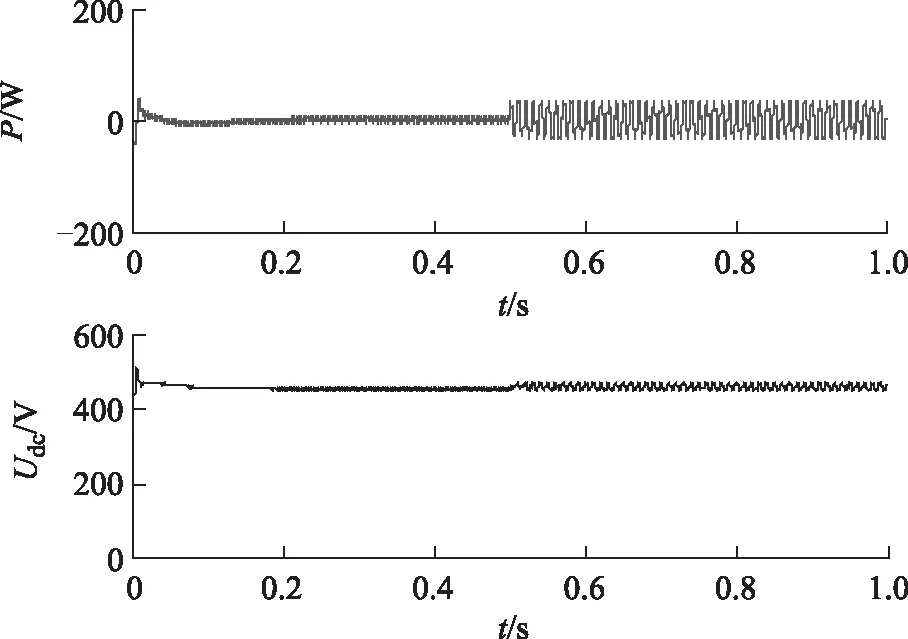
图9 参数k=0，γ=0时仿真结果图Fig.9 Simulation results with k=0 and γ=0

图10为电流表达式中参数k和γ分别从0变化到1时的仿真结果。由图10可见，随着参数k从0到1发生变化，有功功率脉动不断增加。而当k=1时，使γ从0到1变化，并网逆变器无功功率脉动发生明显变化。图10较好地验证了前面的理论分析，参考电流表达式中两个参数对并网质量有很大影响，因此，可通过优化两个系数，实现3个控制目标之间协调优化，从而使并网逆变器发电系整体性能达到最优。

图10 参数k、γ分别从0变化到1时仿真结果图Fig.10 Simulation results with k and γ from 0 to 1

图11为A相电压跌落20%时，自适应整定PI控制器参数KP、KI的变化仿真结果，由图11可见，电网电压发生跌落后，ADALINE神经网络PI能够自适应调整PI参数。

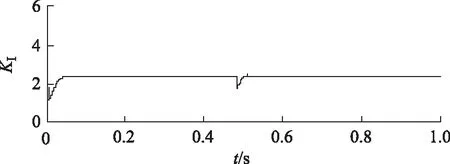
图11 自适应调整KP、KI参数时仿真结果图Fig.11 Simulation results of adaptive PI

4 实验及结果分析

为验证本文提出控制策略的有效性，搭建基于DSP控制板实验系统，系统采用TI公司的TMS320F28335 作为核心控制器，采用两组自耦变压器产生不平衡电压。实验系统参数如表2所示。

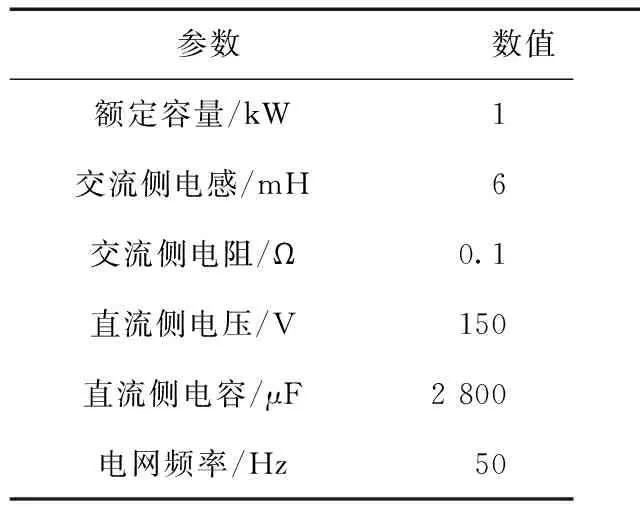
表2 实验参数Tab.2 Experiment parameters

图12～图14分别为电网电压A相跌落20%情况下，系统稳态时控制策略的三相交流侧电流、有功及无功功率实验波形。为分析问题方便，选取有功功率波动、无功功率波动[11]及总电流谐波畸变率[12]为验证控制策略性能的指标，详细分析和求取方法参见文献[11，12]。图12为k=1、γ=1时实验结果图，由图12可知，此时控制策略只实现控制目标1，三相电流平衡且保持良好正弦度，但有功功率和无功功率存在二倍频波动，与前面理论分析和仿真结果一致。

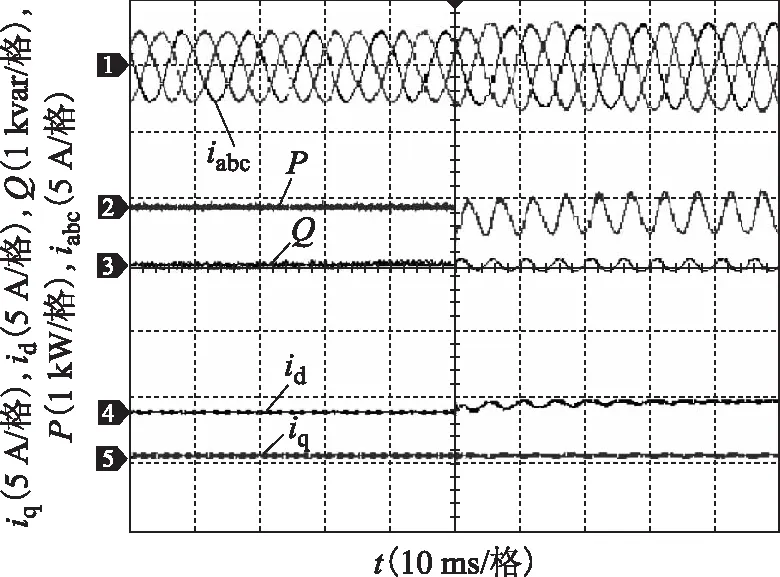
图12 参数k=1，γ=1时实验结果图Fig.12 Experiment results with k=1 and γ=1

图13 参数k=0，γ=0时实验结果图Fig.13 Experiment results with k=0 and γ=0

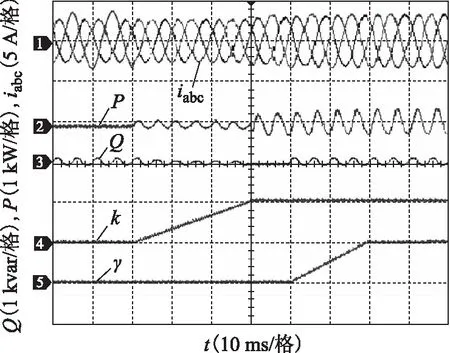
图14 参数k和γ分别从0到1发生变化时实验结果图Fig.14 Experiment results with parameter k and γ adjusted from 0 to 1

图13为k=0、γ=0时实验结果图，从图13中可看出，有功功率保持恒定，三相并网电流虽然保持正弦但失去平衡，无功功率仍存在波动，此时实现控制目标2。图14为两个参数k、γ分别从0变化到1时实验结果图。从图14中可看出，随着两个参数的不断变化，控制的效果也明显不同，当k值不断增大，系统的谐波不断增加，而当γ的不断增加，使得有功功率的波动不断加强。因此，有必要根据实际工作要求，求解两个参数的最优解。

图15为电网电压发生单相跌落20%时RBF神经网络自适应整定PI控制器参数KP、KI变化波形和并网电流波形，从图中可以看出，当电网电压发生变化时，并网逆变器的并网电流较之传统PI控制器性能得到改善。控制器参数KP、KI随电网电压变化在线自适应整定，电网电压跌落后，参数KP变化不大，但KI发生较明显的变化，由正常情况下KI=0.007 94变化到0.009 14。

表3为k、γ不同数值下逆变器有功功率变化、无功功率变化以及总谐波畸变率的计算值。当k=0.874、γ=0.227时，ΔP为15.6%、ΔQ为21.3%，而THD(i)为4.5%，在所有参数组合中间整体性能最优。结果表明在最优参数情况下，能较好兼顾各控制指标，使得整体性能达到最优。

图15 电网电压跌落20%时自适应整定PI实验结果图Fig.15 Experiment results of adaptive PI under grid voltage dip with 20%

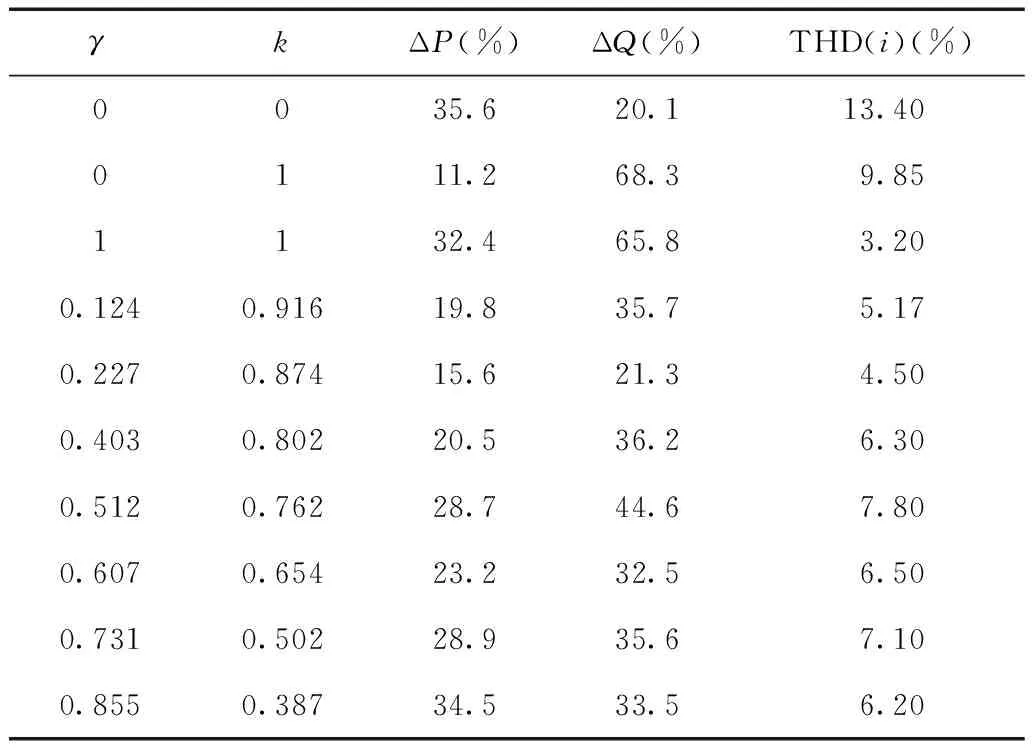
γkΔP(%)ΔQ(%)THD(i)(%)0035.620.113.400111.268.39.851132.465.83.200.1240.91619.835.75.170.2270.87415.621.34.500.4030.80220.536.26.300.5120.76228.744.67.800.6070.65423.232.56.500.7310.50228.935.67.100.8550.38734.533.56.20

实验过程中，暂未考虑电网电压负序分量对锁相环性能影响。事实上，网侧电压有负序时，锁相环算法产生的相位信号也会出现波动，如何消除电网不平衡情况下锁相环性能对坐标变换和相序分离的影响，有待进一步研究。

5 结论

针对不平衡电网情况下并网逆变器控制无法同时实现有功功率恒定、消除负序电流和消除无功功率脉动3个控制目标的问题，提出一种基于ADA-LINE神经网络和RBF神经网络的多目标协调控制策略。建立基于多控制目标统一参考电流矢量表达式，利用ADALINE神经网络在线辨识表达式最优系数，从而实现多控制目标协调控制。为提高内环电流控制的自适应性，采用RBF神经网络在线整定PI控制器参数。仿真和实验结果表明该方法能较好兼顾多个控制目标，使整体控制性能达到最优，并具有较强的鲁棒性。

[1] 王萌，夏长亮，宋战锋，等.不平衡电网电压条件下PWM 整流器功率谐振补偿控制策略[J].中国电机工程学报，2012，32(21)：46-53. Wang Meng，Xia Changliang，Song Zhanfeng，et al.A power resonance compensation control strategy for PWM rectifiers under unbalanced grid voltage conditions[J].Proceedings of the CSEE，2012，32(21)：46-53.

[2] Castilla M，Miret J，Camacho A，et al.Modeling and design of voltage support control schemes for three-phase inverters operating under unbalanced grid conditions[J].IEEE Transactions on Power Electronics，2014，29(11)：6139-6150.

[3] 刘伟增，周洪伟，张磊，等.电网不平衡条件下光伏并网控制策略研究[J].太阳能学报，2013，34(4)：647-653. Liu Weizeng，Zhou Hongwei，Zhang Lei，et al.Study on control strategy of grid connected PV inverter under unbalance grid conditions[J].Acta Energiae Solaris Sinica，2013，34(4)：647-653.

[4] 耿强，夏长亮，阎彦，等.电网电压不平衡情况下PWM 整流器恒频直接功率控制[J].中国电机工程学报，2010，30(36)：79-85. Geng Qiang，Xia Changliang，Yan Yan，et al.Direct power control in constant switching frequency for pwm rectifier under unbalanced grid voltage conditions[J].Proceedings of the CSEE，2010，30(36)：79-85.

[5] Song H S，Nam K.Dual current control scheme for PWM converter under unbalanced input voltage conditions[J].IEEE Transactions on Industrial Electronics，1999，46(5)：953-959.

[6] 年珩，程鹏.电网电压不平衡时PWM 整流器的谐振直接功率控制策略[J].电工技术学报，2013，28(11)：86-95. Nian Heng，Cheng Peng.Resonant based direct power control strategy for PWM rectifier under unbalanced grid voltage condition[J].Transactions of China Electrotechnical Society，2013，28(11)：86-95.

[7] Castilla M，Miret J，Sosa J L，et al.Grid-fault control scheme for three-phase photovoltaic inverters with adjustable power quality characteristics[J].IEEE Transactions on Power Electronics，2010，25(12)：2930-2940.

[8] 郭小强，邬伟扬，漆汉宏.电网电压畸变不平衡情况下三相光伏并网逆变器控制策略[J].中国电机工程学报，2013，33(3)：22-29. Guo Xiaoqiang，Wu Weiyang，Qi Hanhong.Control strategies of three-phase PV grid-connected inverter under distorted and unbalanced voltage conditions[J].Proceedings of the CSEE，2013，33(3)：22-29.

[9] 赵新，金新民，周飞，等.基于比例积分-降阶谐振调节器的并网逆变器不平衡控制[J].中国电机工程学报，2013，33(19)：84-92. Zhao Xin，Jin Xinmin，Zhou Fei，et al.Unbalanced control of grid-connected inverters based on proportion integral and reduced order resonant controllers[J].Proceedings of the CSEE，2013，33(19)：84-92.

[10]Rodriguez P，Timbus A V.Flexible active power control of distributed power generation systems during grid faults[J].IEEE Transactions on Industrial Electronics，2007，54(5)：2583-2592.

[11]Wang F，Duarte J L，Hendrix M A M.Design and analysis of active power control strategies for distributed generation inverters under unbalanced grid faults[J].Generation Transmission & Distribution，IET，2010，4(8)：905-916.

[12]王强钢，周念成，颜伟，等.电网电压不平衡下光伏发电系统的改进功率控制[J].中国电机工程学报，2013，33(z1)：30-37. Wang Qianggang，Zhou Niancheng，Yan Wei，et al.Improved power control of photovoltaic generation system under unbalanced grid voltage conditions[J].Proceedings of the CSEE，2013，33(z1)：30-37.

[13]Mohamed Y A R I，El-Saadany E F.A robust natural-frame-based interfacing scheme for grid-connected distributed generation inverters[J].IEEE Transactions on Energy Conversion，2011，26(3)：728-736.

[14]郭小强，张学，卢志刚，等.不平衡电网电压下光伏并网逆变器功率/电流质量协调控制策略[J].中国电机工程学报，2014，34(3)：346-353. Guo Xiaoqiang，Zhang Xue，Lu Zhigang，et al.Coordinate control of power and current quality for grid-connected PV inverters under unbalanced grid voltage[J].Proceedings of the CSEE，2014，34(3)：346-353.

[15]Widrow B，Lehr M A.30 years of adaptive neural networks：percentron，madaline，and back propagation[J].Proceedings of the IEEE，1990，78(9)：1415-1442.

[16]Abdeslam D O，Wira P，Merckle J，et al.A unified artificial neural network architecture for active power filters[J].IEEE Transactions on Industrial Electron，2007，54(1)：61-76.

[17]刘侃，章兢.基于自适应线性元件神经网络的表面式永磁同步电机参数在线辨识[J].中国电机工程学报，2010，30(30)：68-73. Liu Kan，Zhang Jing.Adaline neural network based online parameter estimation for surface-mounted permanent magnet synchronous machines[J].Proceedings of the CSEE，2010，30(30)：68-73.

[18]郭旭刚，金新民，马添翼，等.电网不平衡下基于滑模变结构的三相电压型PWM整流器恒频控制[J].电力系统保护与控制，2013，41(10)：126-133. Guo Xugang，Jin Xinmin，Ma Tianyi，et al.Constant frequency control for three-phase voltage PWM rectifier under unbalanced grid voltage conditions based on sliding mode control[J].Power System Protection and Control，2013，41(10)：126-133.

[19]年珩，於妮飒，曾嵘.不平衡电压下并网逆变器的预测电流控制技术[J].电网技术，2013，37(5)：1223-1229. Nian Heng，Yu Nisa，Zeng Rong.Predictive current control for grid-connected inverters under unbalanced grid voltage[J].Power System Technology，2013，37(5)：1223-1229.

[20]王久和，杨秀嫒.电网不平衡时电压型PWM整流器控制策略[J].中国电机工程学报，2011，31(18)：14-20. Wang Jiuhe，Yang Xiuyuan.Control strategy of voltage source PWM rectifiers under unbalanced voltage conditions[J].Proceedings of the CSEE，2011，31(18)：14-20.

[21]Rodriguez P，Luna A，Santiago Munoz-Aguilar R S，et al.A stationary reference frame grid synchronization system for three-phase grid-connected power converters under adverse grid conditions[J].IEEE Transactions on Power Electronics，2012，27(1)：99-112.

[22]周林，张林强，李怀花，等.光伏并网逆变器负序分量补偿法控制策略[J].高电压技术，2013，39(5)：1197-1203. Zhou Lin，Zhang Linqiang，Li Huaihua，et al.Negative component compensation control scheme for photovoltaic grid-connected inverter[J].High Voltage Engineering，2013，39(5)：1197-1203.

Research on Multi-objective Coordinated Control Strategies of Grid-connected Inverter Under Unbalanced Voltage Conditions

YangTongguang1，2GuiWeihua2

(1.College of Information Science and Engineering Hunan City University Yiyang 413000 China 2.College of Information Science and Engineering Central South University Changsha 410083 China)

Under unbalanced power grid voltage conditions，the fluctuating active power and current have quadratic ripples and distortions in the grid-connected inverters.In order to improve the quality of the grid-connected current，and reduce the impacts to the grid caused by the grid-connected inverter effectively，a grid-connected inverter control strategy based on the neural network is proposed.The unified analytic formula of the control target is established based on the instantaneous power and the accordingly derived output reference current.An ADALINE neural network is use to optimize the coefficient of the reference current vector formula.In order to improve the system anti-interference capability，a RBF neural network is used to adjust the parameters of the PI controller on-line.The effectiveness and applicability of the proposed strategy are finally verified by simulation and experimental results.

Grid voltage unbalance，grid-connected inverter，multi-objective coordinated control，neural network

国家自然科学基金重点项目(61321003)，国家自然科学基金(51377050)和湖南省教育厅重点项目(13A011)资助。

2014-11-21 改稿日期2015-02-17

TM315