泵站优化运行研究及展望

宋为威，周济人，周文书

泵站优化运行研究及展望

宋为威，周济人，周文书

（扬州大学 水利与能源动力工程学院，江苏 扬州 225009）

随着泵站工程的不断发展，其优化运行也逐渐进入深层次的研究。对单级泵站及梯级泵站优化运行研究，用动态规划法、大系统动态规划法及大系统分解协调技术建立模型，较为全面的约束条件使得数学模型更为严谨。

单级泵站；梯级泵站：优化运行；动态规划法；大系统动态规划法

0 引言

中国有着广袤的平原、河网、圩区，分布着50多万座泵站抗御洪水干旱等自然灾害。随着泵站工程的规模扩大和复杂程度的提高，泵站运行管理也越来越重要。长期以来，泵站的现场运行多依据经验来调节，因而泵站机组难以在效率最高的工况下运行，从而造成了大量的电能损失。或者是，由于泵站运行调度不合理，造成弃水量过多。泵站科学管理的优化技术是指，在一定的时间内，按照一定的最优准则，在满足各个约束条件下，泵站运行目标函数达到最大或最小。由于梯级泵站是一个复杂系统，在优化运行过程中，还应充分考虑到环境、资源、社会、经济等多方面因素［1］。笔者对单级泵站和梯级泵站优化运行研究状况进行概述，对泵站优化运行的进一步研究具有重要意义。

1 单级泵站优化运行研究

单级泵站的优化运行是指，在总的供水量一定的情况下，确定各个阶段最佳分配的供水流量，各个阶段开机的最佳组合及单泵最佳流量、运行工况。泵站优化运行的原则有［2］：耗能最少、机组效率最高、提水效益最大、提水量最大、泵站运行成本最小。其目标函数的求解方法有动态规划法和大系统规划法。

1.1 单级泵站动态规划法

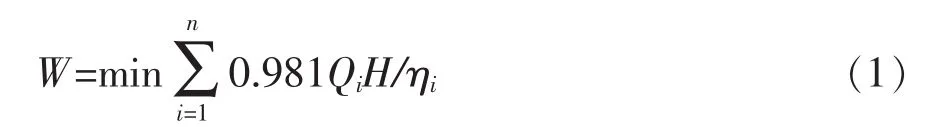
1）汪安南［3］提出以大型全调节轴流泵站运行费用最小为优化目标，其目标函数如公式（1）所示。式中：Qi为第i台水泵的运行流量（Qi＝0表示第i台机组不投入运行，i＝1，2，3…，n），m3/s；H为泵站净扬程，m；ηi为第i台水泵的运行效率。

该方程采用动态规划求解，即，确定机组号i为决策阶段，决策变量为机组的运行流量 Qi（第i台机组所分配流量），状态变量为机组编号顺序累计提水流量 ，指标函数为机组能耗，目标函数为泵站各机组能耗总和。根据最优化原理，递推方程为公式（2），状态转移方程为公式（3）。

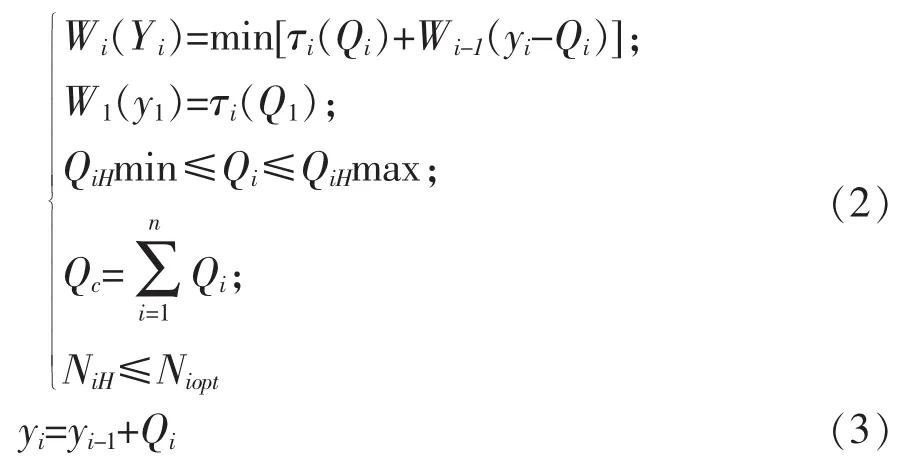
在动态规划的正向过程中，可得出机组最优运行的曲线（Z＝1，2，3，…，n台）及在各种工况下机组的最佳组合。在逆序分析中，可确定工作机组各运行流量。根据水泵流量和扬程，可得到泵叶片运行角度。

2）程吉林等人［4］考虑峰谷电价和泵站下游水位变幅，以单机运行费用最少为优化目标，建立的目标函数如公式（4）所示。决策变量为各时段水泵转速。约束条件为抽水总量的单机组变速优化运行的动态规划，如公式（5）。

式中：f、fi分别表示1d、第i时段的运行电费；Qi（ni）表示第i时段水泵流量；Hi为第i时段时均扬程；SN表示1d分割的运行时段；ΔTi表示第i时段划分时间长；Pi表示第i时段分时电价；We表示下达日提水量； ηzi，ηmot，ηint，ηf分别表示装置效率、电机效率、传动效率、变频效率。

1.2 单级泵站大系统动态规划法

马文正、丘传忻等［5］采用双层动态规划的解法，即大系统动态规划法确定调度的优化决策。即，在未来一段时间内，为达到运行费用最小，确定各类水泵不同时间最优叶片开启度及各泵站开机的台数。

1.2.1 上层动态规划

上层动态规划的目标函数为公式（6），其状态转移方程为公式（7）。

式中：F为泵站系统总运行成本；fm为m泵站（m阶段）成本。

式中：Sm为m泵站未分配抽水任务待分配水量；Sm+1为m泵站分担抽水任务，需由m-1，m-2，…，M泵站分配的抽水量，Dm也是m阶段以后待分配的水量；Dm为m泵站分配的抽水量。

同时，优化过程中，需要满足以下两种约束：（1）状态约束。先确定状态可行域，为避免对无效状态可行性检验。（2）决策约束。QSm≤Dm≤Qm或Dm＝0。其中，QSm指m站一台泵最小叶片角开度研究期内抽水量；Qm为m站所有水泵最大叶片开度工作研究期内的总抽水量。

1.2.2 下层动态规划

下层动态规划的目标函数为公式（8），其状态转移方程为公式（9）。

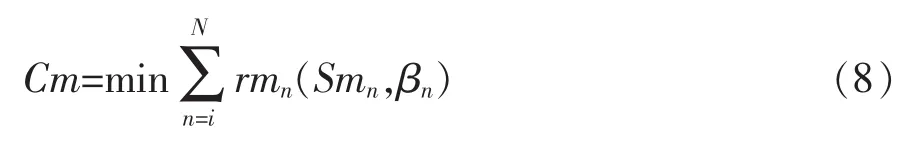
式中：rmn为n时段m站一台泵运行成本；βn为该时段水泵叶片开启角度。

式中：Smn+1、Smn为m泵站在n时段末和时段初待分配水量；Dmn为m泵站 n时段的抽水量；n＝1，2，3，…，N（N是研究时间被划分的时段数）。

优化过程中，应满足以下两个约束条件：（1）状态约束。研究的在运行期内不改变运行期之前所确定开机的台数，开启或停止些水泵运行只可以在下一个运行期，从而避免频繁启闭操作。（2）决策约束。βmin≤βn≤βmax。

2 梯级泵站优化运行研究

梯级泵站的特点是：输水线路长，沿线分水工况复杂，各站间流量、扬程紧密联系，泵站的装机功率大、台数多。梯级泵站优化运行的研究主要有级间流量优化、水位优化两方面。

2.1 梯级泵站动态规划法

1）李继珊等［6］根据多级泵站运行特点，以各级泵站抽取单位水量消耗电能最少为目标，建立的目标函数如式（10）和式（11）所示。

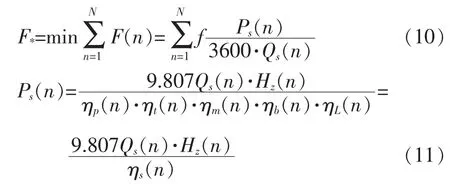
式中：ηp（n）、ηm（n）、ηt（n）、ηL（n）、ηb（n）分别为各级泵站泵效率、电动机效率、传动效率、进水池效率、管路效率；ηs（n）为泵站效率。

状态变量Hs（n）＝{H（1）s（n），H（2）s（n），H（3）s（n），…，H（L）s（n）}T，决策变量 q（n）＝{q（1）（n），q（2）（n），q（3）（n），…，q（L）s（n）}T。

系统方程为：Hs（n+1）＝Tn[Hs（n），q（n）]。其中，（n）为n级干渠放水流量。

优化过程中，应满足以下约束条件：

（1）Qs（n）＝F[Hk（n+1）]（渠首特性方程）；

（2）Qs（n）＝f[H0（n）]（泵站性能方程）；

（3）F[Hk（n+1）]＝f[Hs（n）]（泵站出水流量等于过水渠首流量）；

（4）Hz（n）＝Hk（n）-Hs（n）（泵站净扬程等于进出水池水位差）；

（5）Hsmin（n）≤Hs（n）≤Hsmax（n）（进水池水位约束）；

（6）Hkmin（n）≤Hk（n）≤Hkmax（n）（出水池水位约束）；

（7）|q（n）-q0（n）|＜ε（灌区流量平衡约束）。其中，q0（n）为各灌区各时段需水流量；Hsmax（n）、Hsmin（n）为n级泵站进水池最高和最低水位；Hkmax（n）、Hkmin（n）为n级泵站出水池最高和最低水位。

边界条件：Hs（1）＝Hs0（1）；q（N）＝q0（N）

式中：{Fnq（n），Hs（n）}是在状态Hs（n）做出决策q（n）时消耗的提水费用；F*n[Hs（n）]表示采用最优决策 q*（n）时{Fnq（n），Hs（n）}的最小值。

2）朱满林等［7］建立了级间无分水任务梯级泵站优化的动态规划模型，改善级间流量分配提高梯级泵站效率、降低供水耗能。

他们以梯级泵站年耗能最少为目标建立的目标函数为式（12）。

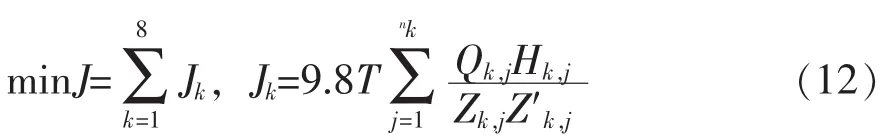
式中：Jk表示 K 级泵站年耗电；Zk，j、Qk，j、Hk，j表示K级泵站第J台泵效率、流量、扬程；Z′k，j表示K级泵站第J台泵电机效率；T表示总运行时间。

系统方程为

式中：QSk-1，k表示第K级和第K-1级泵站间的水量损失，主要包含渠道蒸发和渗漏；QWk-1表示第K-1级泵站产生的弃水量。

递推方程为

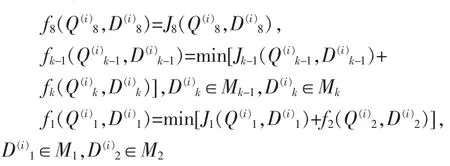
优化过程中，应满足以下约束条件：

（1）QQk≤ QQ（i）k≤ QNk（k＝8，7，…，1）

QRk表示第K级泵站应供给的流量；Xk表示第K级泵站开机方案。

（3）Qk-1≥Qk+QSk-1，k（K＝8，7，…2）（流量连续性约束）。Angl]。

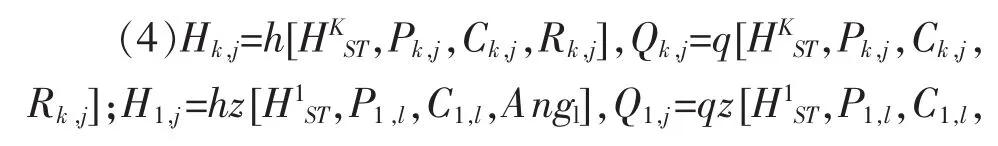
2.2 梯级泵站大系统动态规划法

刘德祥等［8］运用大系统优化理论对多级泵站优化运行进行分析，建立三层递阶结构的大系统分解协调、分解聚合模型。

2.2.1 第一层子系统（站内）机组优化模型

该系统的系统方程为

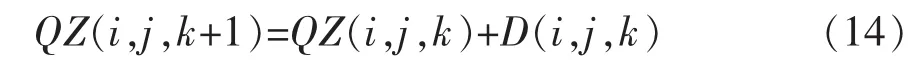
式中：QZ（i，j，k+1）、QZ（i，j，k）表示前k及k-1台机组提水流量的累积；D（i，j，k）表示第k台机组提水流量。

以单位提水量能耗最小为优化目标的目标函数为

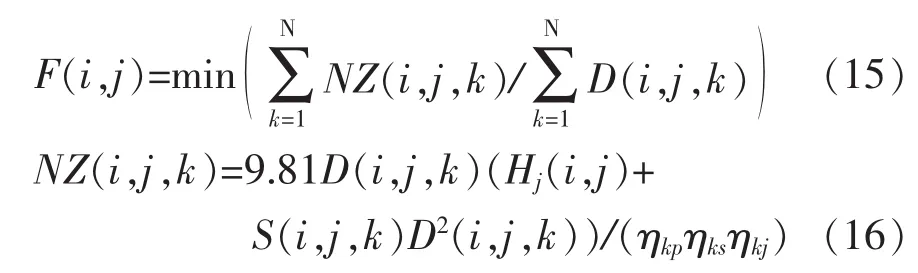
式中：S（i，j，k）表示机组管路阻力系数；Hj（i，j）表示泵站净扬程；NZ（i，j，k）表示输入功率；ηkp、ηks、ηkj表示k台机组水泵效率、传动效率、电机效率。

优化过程中，应满足以下约束条件：

（1）ZS（i，j）＝ZG（Q W（i，j））（出水池水位与流量约束）；

（泵站总流量约束）。

2.2.2 第二层分系统（多级泵站与概化泵站）优化模型

该系统的系统方程为

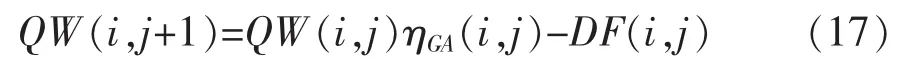
式中：ηGA（i，j）表示第i分系统第j级干渠水利用系数。

以经济效益最大化＝供水效益-供水成本为优化目标建立的目标函数为

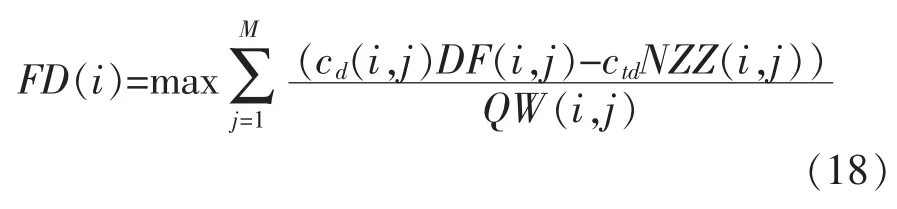
式中：cd（i，j）表示单位供水经济利益；ctd表示电费单价；NZZ（i，j）表示第j级泵站单位时间总耗能，

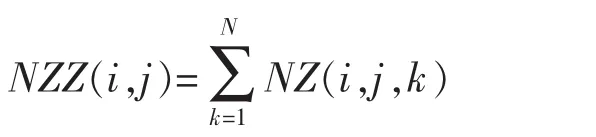
优化过程中，应满足以下约束条件：

（1）QS1（i，j）≤Q W（i，j）≤Q Sm（i，j），Q W（i，j）≤Q W（i，j-1）（状态约束）；

（2）DF（i，j）≥DG1（i，j）或DF（i，j）＝0，DF（i，j）≤DFm（i，j）（决策约束）；（3）Z1（i，j）≤ZZ（i，j）≤Zm（i，j）（干渠水位约束）；（4）QW（i，1）＝W（i），QW（i，M+1）＝0（边界约束）。

2.2.3 第三层（泵站群）优化大系统协调模型

以系统经济效益最大为优化目标建立的目标函数为

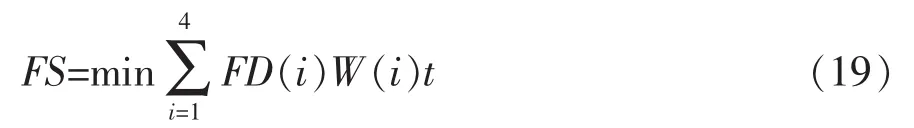
式中：t表示一次灌溉时间。

优化过程中，应满足以下约束条件：

（1）W（i）≤Q W（i）（最大提水能力约束）；

（2）W（i）≤Q D（i，SW（i））（引水渠过水能力约束）；

（3）SW（3）＝ZZ4（SW（4），W（4）），SW（2）＝ZZ3（SW（3），W（3）），SW（1）＝ZZ2（SW（2），W（2）），（取水口耦合约束）；

（4）W（i）≥0（决策变量非负约束）。

3 结语

随着最优化理论和方法的完善，遗传算法、神经网络等计算方法将运用于泵站的优化运行中。泵站作为水资源系统的重要环节，对泵站优化运行研究更应该从水资源大系统全面考虑。梯级泵站优化运行研究将随着我国跨流域和跨区域调水的运行而具有更重要的意义。

［1］贾仁甫，金明宇，王红，等.国内泵站优化调度研究的发展现状［J］.河南科技大学学报：自然科学版，2005，26（6）：96-99.

［2］袁尧，刘超.蚁群算法在泵站单机组优化运行中的应用［J］.水力发电学报，2013，32（1）：263.

［3］汪安南，伍杰.大型轴流泵站最优运行方式探讨［J］.农田水利与小水电，1993（11）：36-38.

［4］程吉林，张礼华，张仁田，等.泵站单机组变速运行优化方法研究［J］.农业机械学报，2010，41（3）：72-73.

［5］马文正，丘传忻，贺贵明.泵站运行的优化调度［J］.水利学报，1993（11）：35-37.

［6］李继珊，刘光临，潘为平.多级泵站的优化调度及经济运行研究［J］.水利学报，1992（12）：18-23.

［7］朱满林，杨晓东，张言禾.梯级泵站优化调度研究［J］.西安理工大学学报，1999，15（1）：67-70.

［8］刘德祥，何忠人，郑玉春，等.大岗坡一石台寺多级泵站群优化调度模型研究［J］.水电能源科学，1995，13（4）：236-239.

[责任编辑 杨明庆]

Research and Outlook on Pumping Station Optimal Operation

SONG Wei-wei,ZHOU Ji-ren,ZHOU Wen-shu
(Yangzhou University,Yangzhou 225009,Jiangsu,China)

With the development of pumping station engineering,the optimal operation research has reached a new level.The optimal operation of single-stage and multi-step pumping station are studied.The model is built by using dynamic programming method,large-scale system dynamic programming method and large-scale system decompose-coordinate technology.The more comprehensive constraint condition makes the mathematic model more preciseness.

Single-stage pumping station;multi-step pumping station;optimal operation;dynamic programming method;large-scale system dynamic programming method

TV675

A

1008-486X（2015）03-0010-04

2015-05-29

宋为威（1991-），男，江苏盐城人，硕士研究生，主要从事泵站工程及跨流域调水专业的学习与研究工作。