基于灰色加权马尔可夫链的大连铁路客运量预测

贾金平，吉莉

(大连科技学院 基础部，辽宁 大连 116052)



基于灰色加权马尔可夫链的大连铁路客运量预测

贾金平，吉莉

(大连科技学院 基础部，辽宁 大连 116052)

以2003～2013年大连铁路客运量数据为基础，采用灰色GM(1,1)模型预测方法和马尔可夫链相结合的方法对大连铁路客运量数据进行预测，给出了灰色加权马尔科夫链预测模型.不仅构造了状态转移概率矩阵，而且也获得了有效的滞时阶数.结果表明，在预测值与真实值的平均绝对误差方面，与灰色GM(1,1)模型相比，灰色加权马尔可夫链模型减小了一半，其预测效果十分理想.在此基础上，对2014～2020年大连铁路客运量数据进行了预测.

GM(1,1)模型；加权马尔科夫链；铁路客运量

0 引言

灰色系统理论是邓聚龙教授在上个世纪八十年代首创，对于信息不完全系统的分析与预测具有十分独特的功效.灰色预测模型是当时间序列数据样本十分稀少时对未来趋势进行预测的方法[1].以“灰色预测”为主题检索中国知网，最近几年发表在期刊上的论文数量平均每年都有400多篇，并呈现逐年递增趋势.荣文竽[2]根据2003～2008年大连火车站客运量数据，使用灰色系统方法预测2012和2013年客运量分别为1 637.3万人和1 777.6万人.但是，这两年客运量真实值为1 245.3万人和1 423.3万人，误差为-31.5%和-24.9%.误差如此之大的原因是，灰色系统预测对短期数据的预测效果比较理想，而对长期数据的预测效果会越来越差.

在旅客客运量预测方面，一些学者使用神经网络[3]、遗传算法[4]、马尔科夫链[5]、线性回归马尔科夫链[6]等数学方法进行了有益的尝试.作为进一步研究，笔者拟对灰色系统预测模型的结果进行加权马尔可夫链，从而提高对大连铁路客运量预测的准确性，为大连铁路客运量的精确预测提供更加可靠的方法依据.

1 基于GM(1,1)模型的铁路客运量预测

1.1 GM(1,1)模型

根据上述原理，使用2003～2013年共11年大连铁路客运量实测数据，在灰色系统专业预测软件GSTAV7.0平台上得到2003～2020年的客运量的预测数据.对2003～2013年大连铁路客运量的实测值与GM(1,1)模型预测值进行比较，如表1所示.

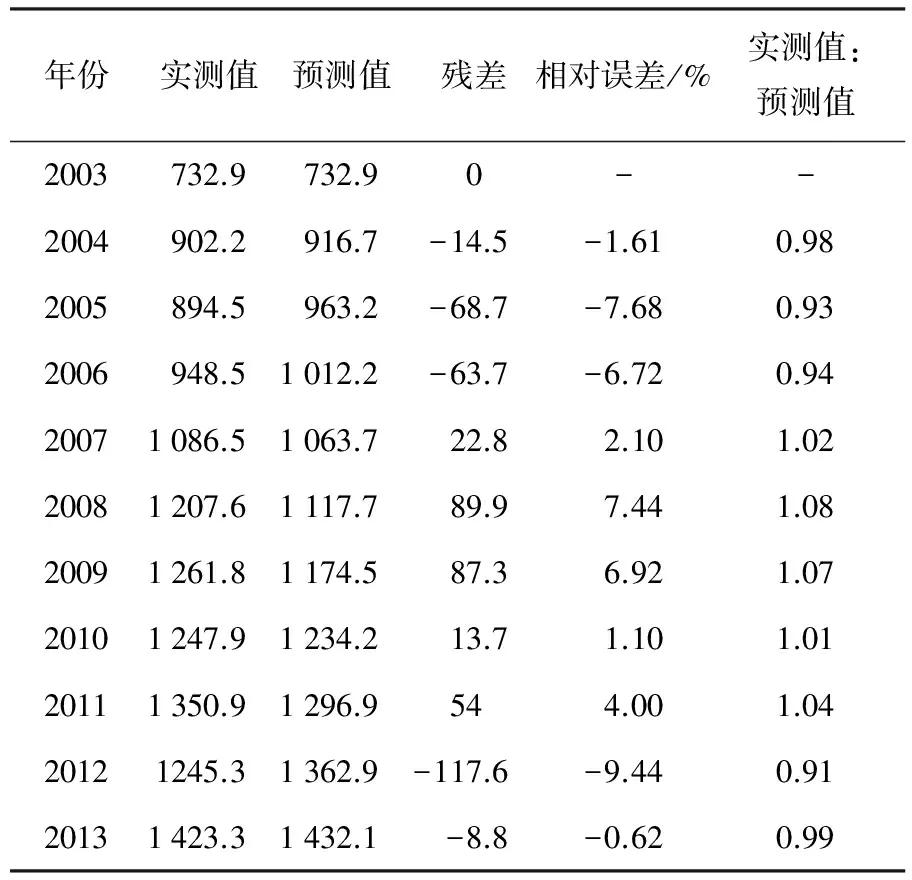
表1 大连铁路客运量的GM(1,1)模型预测值 万人

1.2 结果检验

其中，S1为原始序列的方差，S2为残差的方差.

小误差概率

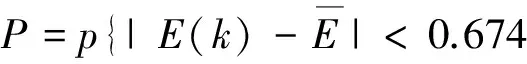
5S1}=1

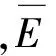
根据表2，C和P值显示预测精度都达到了1级水平，但是有些预测数据的误差较大，因此有必要进一步改进GM(1,1)模型的预测结果.

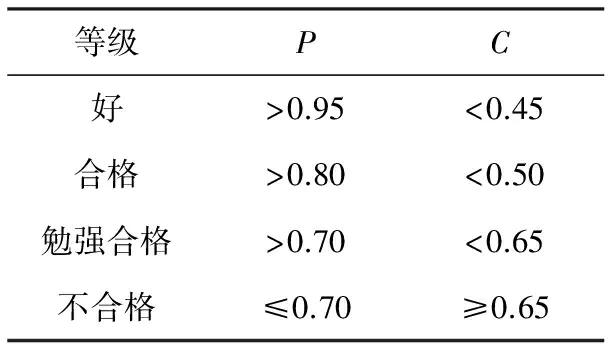
表2 预测精度等级表

2 模型在铁路客运量预测中的应用

2.1 状态的划分

根据表1中大连铁路客运实测值与GM(1,1)模型预测值的比值情况，将2003～2013年的数据划分为4种状态：E1(0.91～0.95)，E2(0.96～1.00)，E3(1.01～1.05)，E4(1.06～1.10).各状态的中值分别为：Z1=0.93,Z2=0.98,Z3=1.03,Z4=1.08.

因此每年的状态如表3所示.

表3 每年的状态

2.2 各阶自相关系数的计算

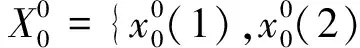
根据上述公式，计算大连铁路客运量原始时间序列数据的各阶自相关系数，前6阶自相关性系数为：r1=0.847 1,r2=0.931 0,r3=0.950 3,r4=0.820 1,r5=0.688 7,r6=0.596 7.前三阶自相关性逐渐加强，随后逐渐快速减弱，由此可见，我们只需要考虑前3阶自相关系数即可.将前三阶自相关系数归一化后作为各自滞时的马尔可夫链的权重，分别为：ω1=0.310 5,ω2=0.341 2,ω3=0.348 3.

2.3 构造状态转移概率矩阵

构造如下状态转移概率矩阵[7]

其中,Pij(a)=Mij(a)/Mi,i=1,2,…,N;Mij(a)表示状态i经过a步转移到状态j的原始数据的个数;Mi是处于状态i的原始数据个数.

根据表3状态划分和滞时阶数，获得步长分别为a=1,2,3的马尔可夫链状态转移概率矩阵：

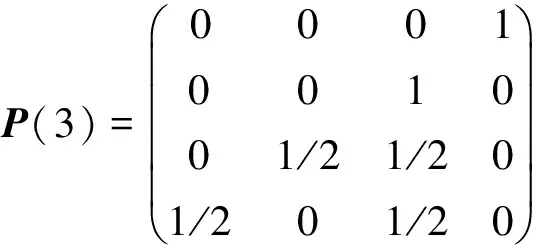
2.4 预测原始序列

根据大连铁路客运量的实测值及相应的状态转移概率矩阵对2014年数据进行预测，其结果如表4所示.通过GM(1,1)模型得到2014年预测值是1 504.9.根据加权马尔科夫链模型预测出来的权是0.998 772 5，从而2014年预测值是1 503.1.

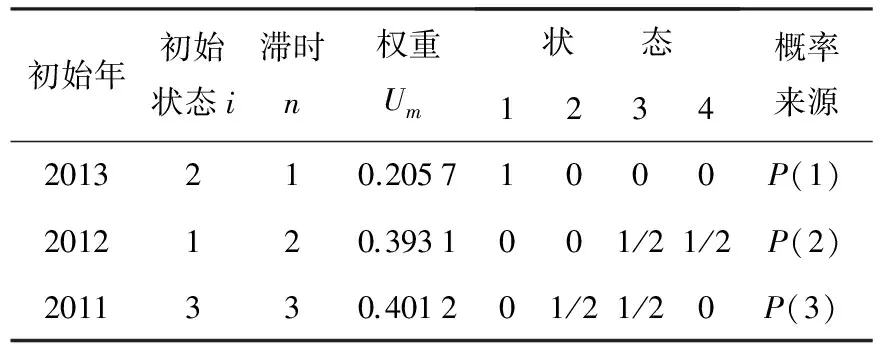
表4 2014年大连铁路客运量预测

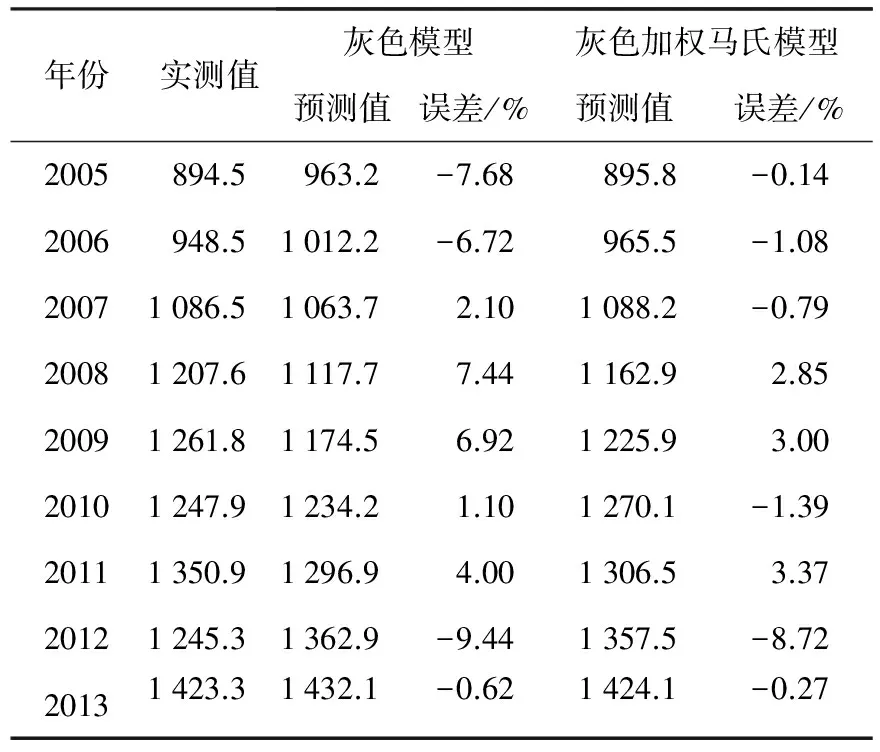
表5 大连铁路客运量预测值比较 万人

表5给出了灰色加权马尔可夫链模型与灰色GM(1,1)模型预测值与精度的比较.在预测值与实测值的平均相对误差方面，误差灰色GM(1,1)模型为-0.32%，灰色加权马尔可夫链模型为-0.35%.在预测值与实测值的平均绝对误差方面，误差灰色GM(1,1)模型为5.11%，灰色加权马尔可夫链模型为2.53%.由此可见，与灰色GM(1,1)模型相比，灰色加权马尔可夫链模型的预测效果明显更加理想.于是，灰色加权马尔科夫链模型对2014～2020年大连铁路客运量进行了预测，预测结果分别为1 503.0、1 594.2、1 684.2、1 754.5、1 796.2、1 843.7、1 955.0万人.

3 结论

针对灰色GM(1,1)模型受原始数据影响较大，其预测精确度不高这一缺点，对大连铁路客运量预测采用了灰色加权马尔科夫链改进预测方法的研究思路.选取2003～2013年大连铁路客运量数据进行模拟，建立了灰色GM(1,1)模型，并对该模型进行数据模拟检验，此模型可以用于大连铁路客运量的预测.对灰色模型进行加权马尔可夫链修正，并对未来7年大连铁路客运量进行了预测.不仅构造了状态转移概率矩阵，而且也获得了滞时阶数，预测结果的准确性和效度得到了较大的改进.

[1]刘思峰,杨英杰,吴利丰.灰色系统理论及其应用[M].北京:科学出版社,2014．

[2]荣文竽,梁立,王洪亮.哈大客运专线长大段趋势客运量预测[J].大连交通大学学报,2011,32(1):22-25.

[3]吴昕慧.基于神经网络的铁路客运量优化预测[J].计算机仿真,2010,27(10):168-174.

[4]甘秋明.基于遗传算法优化支持向量机的公路客运量预测[J].公路工程，2012,37(6):192-195.

[5]娄彦江,马艳丽,韩丽飞.基于马尔科夫链的区域综合交通客运结构预测[J].交通运输系统工程与信息，2012,12(3):1-5.

[6]李晓东.基于线性回归马尔可夫模型的铁路客运量预测[J].铁路运输与经济,2012(4):38-41.

[7]王增民,王开珏.基于灰色加权马尔可夫链的移动通信市场预测[J].数学的实践与认识,2012,42(24):8-15.

Forecasting of Railway Passenger Based on Gray-Weighted Markov Model

JIA Jinping,JI Li

(Dalian Institute of Science and Technology,Dalian 116052,China)

Based on the number of railway passengers from 2003 to 2013,the GM (1,1) and Markov chain models are used to predict the number of Dalian railway passengers,and Gray-Weighted Markov chain Model is proposed to construct the state transition probability matrix and achieve effective lag order number.The results show that compared with GM (1,1),the mean absolute error of the real value and forecasted data are reduced by half through the gray-weighted Markov chain mJPodel,and the prediction effect is very ideal.On this basis,the number of Dalian railway passenger from 2014 to 2020 is forecasted.

GM(1,1)；weighted Markov chain；number of railway passenger

1673-9590(2015)03-0006-04

2014-11-08

贾金平(1981-),男,讲师,硕士,主要从事大学生数学创新教育的研究E-mail:260115540@qq.com.

A