多腔室穿孔管消声器声学特性分析

郑 晗 周其斗 毛艳蕾

(海军工程大学舰船工程系1) 武汉 430033) (91206部队2) 青岛 266108)

多腔室穿孔管消声器声学特性分析

郑 晗1)周其斗1)毛艳蕾2)

(海军工程大学舰船工程系1)武汉 430033) (91206部队2)青岛 266108)

采用一维解析法和三维有限元法分别预测了穿孔管消声器的声学性能，并与实验值对比，结果表明，三维有限元法能在全频段很好地预报消声器的传递损失.采用有限元法研究了多腔室穿孔管消声器的腔室顺序、腔室数目、腔室划分和腔室间距等因素对其声学性能的影响，结果表明：多腔室穿孔管消声器的传递损失值是组成它的多个单腔室穿孔管消声器传递损失的线性叠加，腔室顺序对传递损失结果没有影响；采用插入障板的方式将单腔室穿孔管消声器划分为多腔室穿孔管消声器，可以有效改善消声器的低中频消声性能；插入障板的位置对阻性和抗性消声器的影响规律不同，障板均等划分对阻性消声器的传递损失增大有利，对抗性消声器则并不一定；腔室间距对传递损失的影响主要体现在峰值数目上，峰值大小基本不变，总体而言，腔室间距为0时，消声器在全频段具有最好的消声性能.

穿孔管消声器；多腔室；传递损失；有限元法

0 引 言

在汽车和船舶噪声控制中，常采用消声器降低通风系统和进排气系统的噪声.穿孔管消声器因为具有良好的空气动力性能和消声性能，在过去十几年里被广泛研究和应用.国外最早出现穿孔管消声器的研究始于Sullivan等[1]，采用一维控制体积法，推导了含有均匀流的同轴穿孔管的传递损失计算公式，并根据实验测得的穿孔声阻抗进行了数值预测，结果与实验值对比良好.Wang[2]，Selamet等[3-4]也分别采用一维解析法、二维解析法和边界元法对穿孔管阻性和抗性消声器性能进行了预报，并研究了吸声材料流阻率、厚度和穿孔率等参数变化对传递损失的影响.国内研究穿孔管消声器的主要有季振林等[5-7]，发展了子结构边界元法和有限元法用于穿孔管消声器的传递损失预测，全面系统地讨论了吸声材料、马赫数、腔室尺寸和穿孔几何等对其消声性能的影响.还有很多学者针对汽车消声器的实际应用，研究了流场[8]、温度场[9]等对消声器性能的影响，所得结果对于消声器的设计具有十分重要的意义.

尽管这些研究已经十分深入并且细化，但其针对的多是单腔室消声器，对于多腔室消声器的声学性能研究以往并不多见.本文将多腔室穿孔管消声器作为研究对象，分别采用一维解析法和三维有限元法验证实验结果，详述了方法实现中的关键问题，比较了它们的优劣，并研究了腔室顺序、数目、划分和间距对消声器声学性能的影响，研究结果对多腔室穿孔管消声器的设计具有积极意义.

1 计算方法与验证

本文分别基于MATLAB和Virtual Lab实现了一维解析法和三维有限元法，2种方法的公式推导分别见文献[2]和[10]，下面重点说明方法实现中的关键问题.

1.1 一维解析法

采用一维解析法计算穿孔管消声器的传递损失(transmission loss，TL)时，一个非常重要的参数就是穿孔管的声阻抗

(1)

式中：tw,dh，φ分别为穿孔管的壁厚、孔径和穿孔率；R为无因次声阻；α为声学厚度修正系数.通常，R和α由经验公式求得.

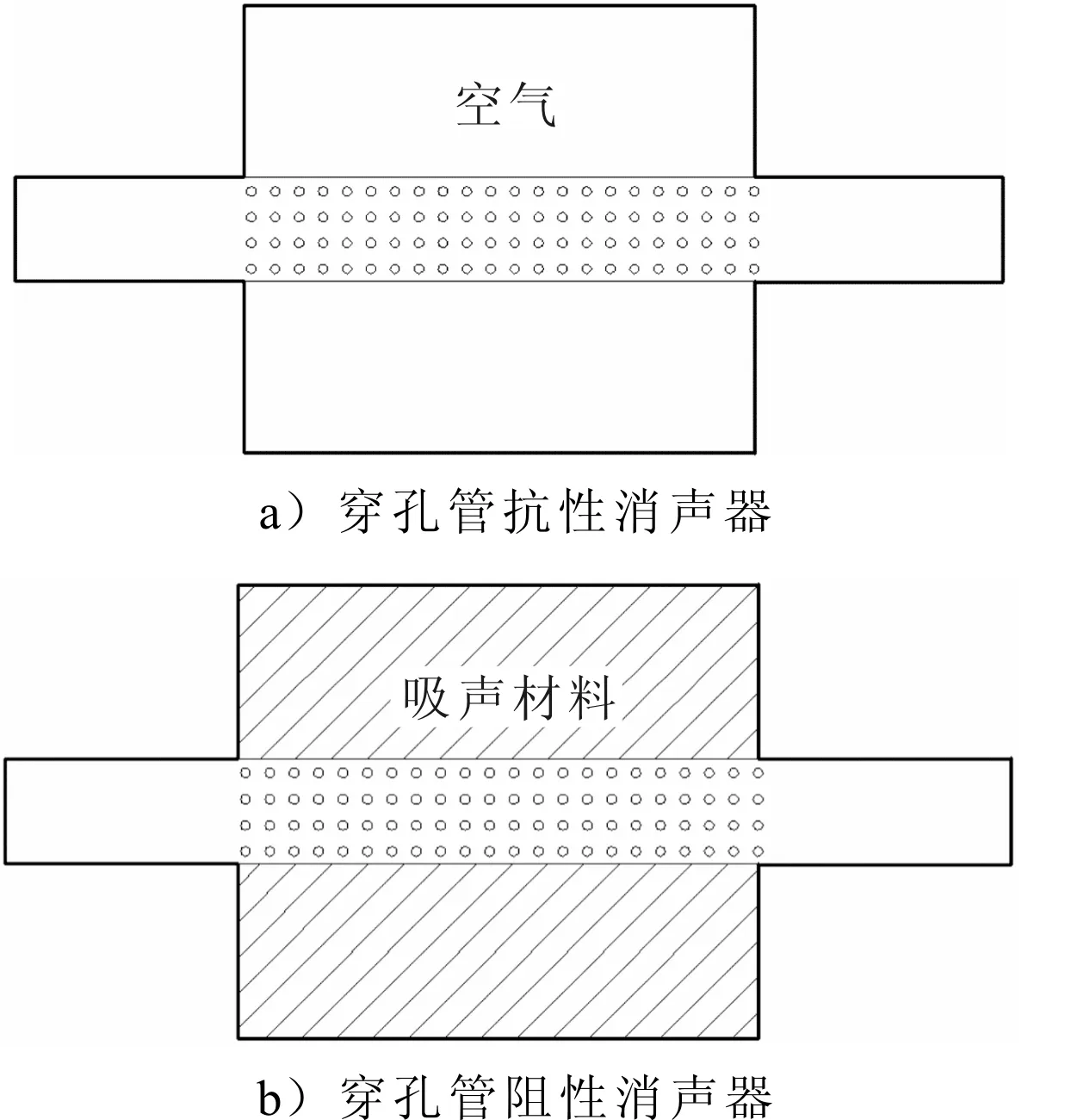
图1 两种穿孔管消声器

图1给出了常见的2种穿孔管消声器.对于穿孔管抗性消声器，过去常用的经验公式由文献[1]给出，针对穿孔率为4.2%的管，测得R=0.006，α=0.75.Melling[11]通过引入Fok函数ψ′(ξ)考虑了孔之间的相互作用，将声学厚度修正系数表示为

(2)

ψ′(ξ)=1-0.409 25ξ+0.338 18ξ3+

0.067 93ξ5-0.022 87ξ6+0.030 15ξ7-

0.016 41ξ8+0.017 29ξ9-0.012 48ξ10+

0.012 05ξ11-0.009 85ξ12

(3)

(4)

式中：S为每个孔占据的平均管壁面积.笔者通过对多个实验算例的验证，最终发现：采用Sullivan公式预测的传递损失结果对于穿孔率在4.2%左右的穿孔管是准确的，对于高穿孔率的管结果偏差很大；采用Melling公式预测的传递损失结果则能适应各个穿孔率的管，因此本文的抗性消声器计算中均采用Melling提出的声阻抗公式.

对于穿孔管阻性消声器，采用Selamet给出的公式

(5)

1.2 三维有限元法

1.2.1 穿孔管声阻抗公式的选取

采用VL计算传递损失时，通常采用的声阻抗表达式为

Zp=Rp+jXp

(6)

当管壁厚度极小时，Rp和Xp的表达式为

(7)

(8)

式中：ε为穿孔率；η为空气的动态粘性系数；ρ0为空气密度；t为管壁厚度；Rh为孔的半径；CF为修正因子，它取决于孔的排列类型、间距d和直径Rh等.当孔的中心为正四边形排列时，有

(9)

求得声阻抗之后，可以进一步得到穿孔管的传递导纳矩阵，即

(10)

式中：α1～α5即为用户输入的传递导纳参数，它是随频率变化的量.

1.2.2 吸声材料的模拟

采用VL模拟吸声材料时，通常把它看作具有复声速和复密度的流体介质，其复声速和复密度由下式决定

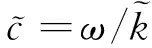
(11)

(12)

本文采用了由Ji[12]推出的复阻抗和复波数公式

(13)

(14)

式中：ρ0，k0，Z0分别为空气的密度、波数和特性阻抗；f为频率；σ为吸声材料的流阻率.

1.3 验证与比较

分别采用一维解析法和三维有限元法对穿孔管消声器的传递损失进行验证.所有实验数据均来自文献[13]，穿孔管消声器的尺寸参数为腔室长L=257.2 mm，内径D2=164.4 mm，穿孔管内径D1=49.0 mm，厚度t=0.9 mm，管内无气流.采用VL计算消声器性能的有限元模型见图2，中间细管内是空气单元，外部腔室内是吸声材料单元.

图2 穿孔管阻性消声器的有限元模型

图3给出了腔室内填充空气时，2种穿孔率φ和孔径dh下的穿孔管抗性消声器传递损失比较结果，可以看出：(1) 一维解析法在低频段与实验值对比很好，高频段因为不能考虑高阶声波模态相差较大，并且，相比而言，一维解析法对于低穿孔率和小孔径的穿孔管消声器预测结果比高穿孔率和大孔径的好；(2) 采用三维有限元法预测的传递损失值与实验值对比很好，在高频段仍能很好地预报出峰值频率和大小.

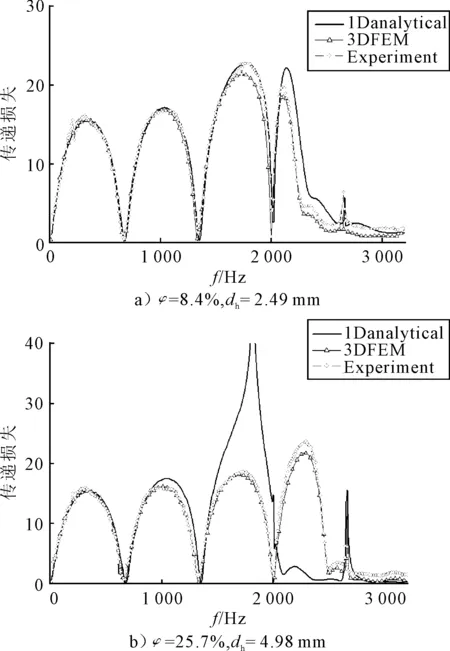
图3 穿孔管抗性消声器的传递损失比较

图4给出了腔室内填充吸声材料时的传递损失比较结果.实验中填充的吸声材料为长丝玻璃纤维，填充密度100 kg/m3，流阻率4 896 Rayl/m.观察图中曲线可以看到，采用一维解析法只在低频段获得与实验值较好的一致性，高频段完全偏离真实结果，而三维有限元法的计算结果则在整个频段与实验结果吻合良好.

图4 穿孔管阻性消声器的传递损失比较

尽管三维有限元法相比一维解析法在高频计算精度上具有无可比拟的优势，一维解析法仍可以作为大量参数计算时的一种辅助方法，因为它无需建模和网格导入等步骤，只需在程序中改动参数就可以获得大量计算结果，从而初步摸清该参数的影响规律.

2 影响因素分析

为便于表达和书写，定义一种命名多腔室消声器的方法，首先命名2个基准消声器：采用“1reac”表示基准穿孔管抗性消声器，它的几何参数为腔室长度L=257.2 mm，内径D2=164.4 mm，穿孔管内径D1=49.0 mm，厚度t=0.9 mm，穿孔率φ=8.4%，孔径dh=2.49 mm；采用“1diss”表示基准穿孔管阻性消声器，其几何参数完全同抗性消声器，区别是填充有密度为ρf=100 kg/m3的长丝玻璃纤维.根据该命名方法，0.5reac表示腔室长度为128.6 mm的抗性消声器，1reac1diss表示长度为257.2 mm的抗性消声器和长度为257.2 mm的阻性消声器组合而成的阻抗复合式消声器，依此类推，见图5.

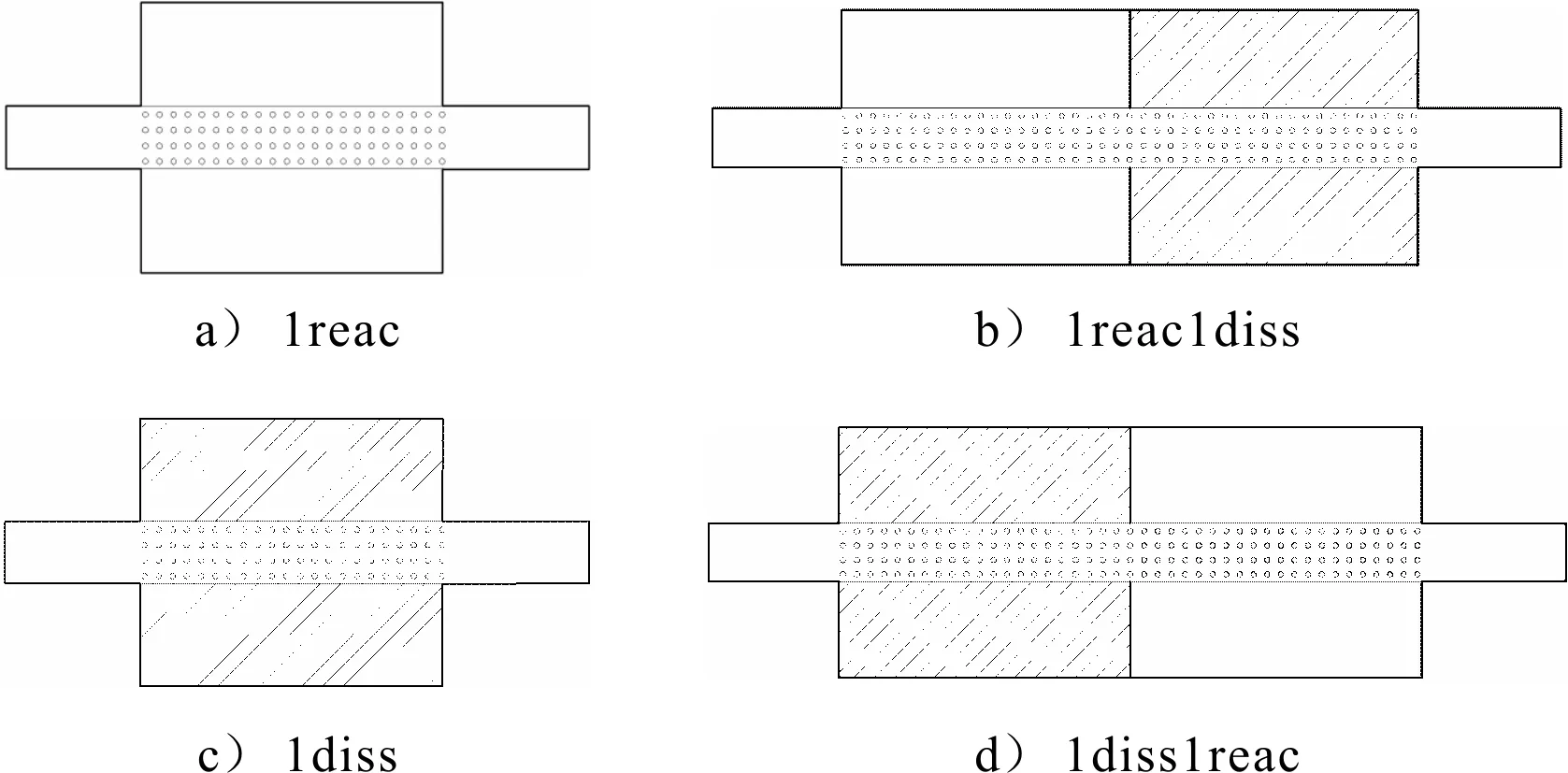
图5 穿孔管消声器的命名举例

2.1 腔室顺序

为研究腔室顺序对一个多腔室阻抗复合式消声器性能的影响，计算了图5中的4种穿孔管消声器(入口均在左端)的传递损失，见图6，从图中可以看出：(1) 除0～300 Hz低频段以外，1reac1diss消声器的传递损失曲线恰好是1reac与1diss的传递损失曲线之和，即串联多腔室消声器的传递损失是组成它的多个单腔室消声器的传递损失的线性叠加；(2) 1reac1diss与1diss1reac的传递损失曲线完全相同，说明对于多腔室消声器，腔室的顺序对传递损失结果没有影响.

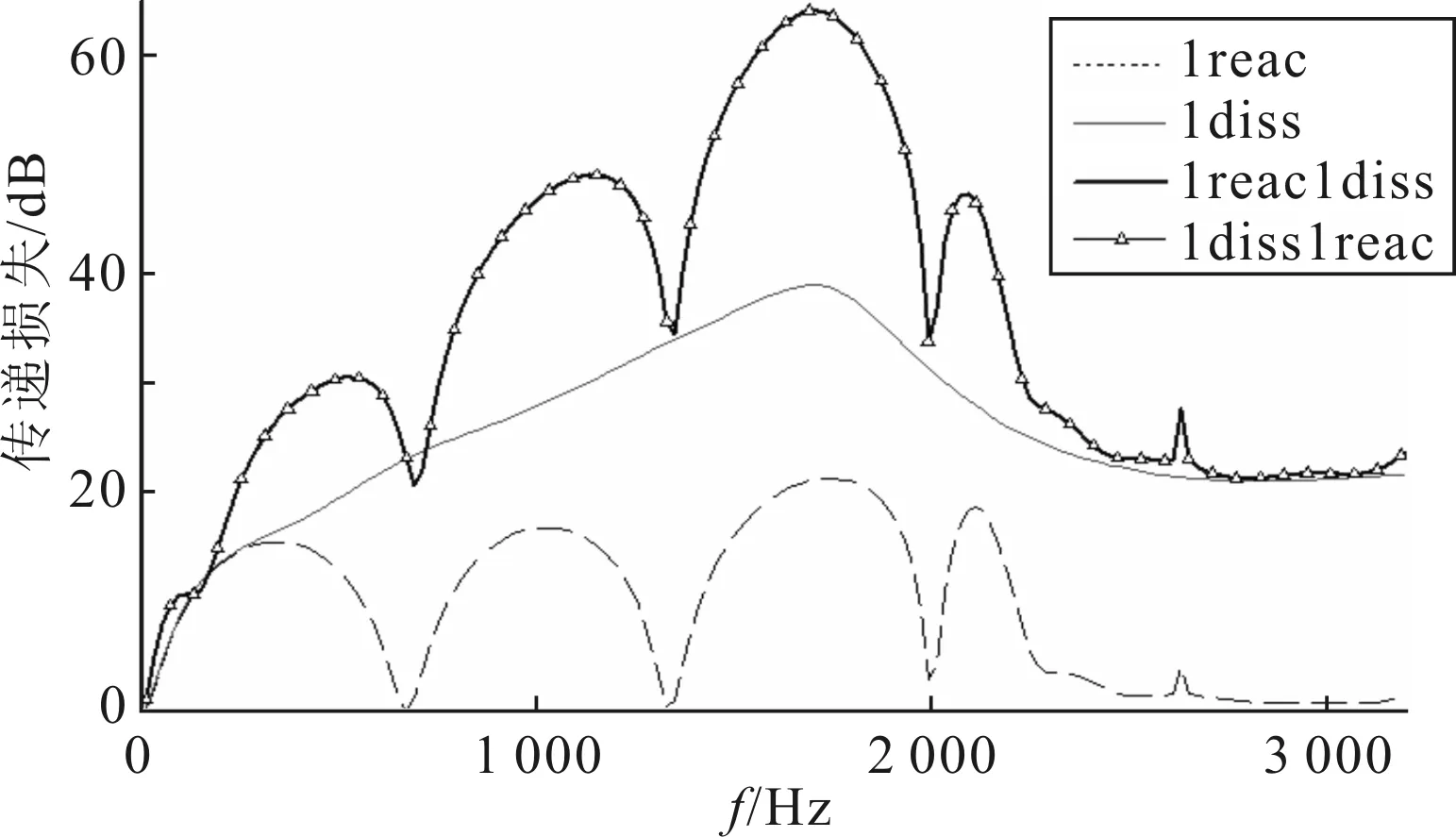
图6 4种穿孔管消声器的传递损失曲线

2.2 腔室数目

首先研究穿孔管抗性消声器的腔室数目对传递损失的影响，固定腔室的总长度，在腔室内通过加入刚性障板的方式将单腔室均分为多个腔室.图7给出了单腔室1reac、两腔室0.5reac0.5reac和三腔室0.33reac0.33reac0.33reac三种抗性消声器的传递损失曲线，同时给出的Expansion Chamber为相同几何尺寸的简单扩张式消声器的传递损失曲线.从图中可以看到：(1) 比较Expansion Chamber和1reac，简单扩张式消声器与穿孔管抗性消声器的传递损失曲线在低中频段几乎重合，只在高频出现一定的差别，这说明穿孔声阻抗影响的主要是高频段的消声性能，低中频段穿孔管抗性消声器的性能预报可以由简单扩张式消声器得到；(2) 比较1reac,0.5reac0.5reac和0.33reac 0.33reac0.33reac，随着腔室数目的增多，抗性消声器传递损失曲线的拱顶数目变少，带宽增大，传递损失的峰值也明显增大.为了解释这一现象，给出简单扩张式消声器的传递损失计算公式

图7 不同数目腔室的穿孔管抗性消声器传递损失曲线

图8给出了1diss，0.5diss0.5diss和0.33diss 0.33diss0.33diss 3种阻性消声器的传递损失曲线，从图中可以看到，随着腔室数目的增多，阻性消声器传递损失曲线的峰值频率降低，峰值增大.消声器第一个消声峰值以前的消声性能有了很大的改善，而峰值以后的消声量变化不大.

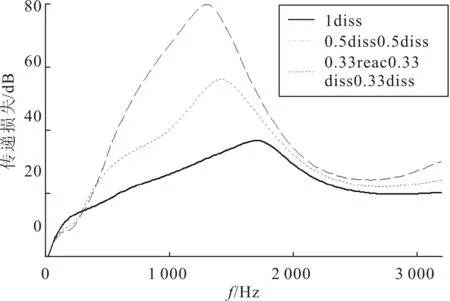
图8 不同数目腔室的穿孔管阻性消声器传递损失曲线

以上结果均表明，采用插入障板的方式将单腔室穿孔管消声器划分为多腔室穿孔管消声器可以有效改善消声器的低中频消声性能.

2.3 腔室划分

采用一块刚性障板，将单腔室消声器划分为不等长的两腔室消声器.图9给出了不同腔室划分状态下的穿孔管消声器传递损失曲线.其中图9a)表示将抗性消声器1reac划分为0.5reac0.5reac，0.25reac0.75reac和0.125reac0.875reac，图9b)与a)类似，表示阻性消声器的划分.

图9 不同腔室划分状态下的穿孔管消声器传递损失曲线

由图9可知，腔室划分对抗性消声器传递损失的影响规律较为复杂，在一些频段(如300～1 000 Hz)，均等划分的传递损失比不均等划分大，而在另一些频段(如1 000～1 500 Hz)则恰好相反.对于阻性消声器，不均等划分的消声器传递损失比均等划分消声器的小，并且两腔室长度差别越大，传递损失越小.也就是说，插入障板的位置对阻性和抗性消声器传递损失的影响规律并不相同，需具体分析.

2.4 腔室间距

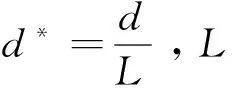
图10 多腔室穿孔管消声器的几何尺寸

图11给出了不同腔室间距下两腔室穿孔管消声器的传递损失曲线.由图11可见，对于三类消声器，腔室间距的影响规律相同，随着距离d的增大，低中频段传递损失曲线的波峰和波谷数目增多，峰值大小基本不变.总体而言，腔室间距为0时，消声器在全频段具有最好的消声性能.

图11 不同腔室间距下消声器的传递损失曲线

3 结 论

1) 串联多腔室穿孔管消声器的传递损失值是组成它的多个单腔室穿孔管消声器传递损失的线性叠加，腔室顺序对传递损失结果没有影响.

2) 采用插入障板的方式将单腔室穿孔管消声器划分为多腔室穿孔管消声器，可以有效改善消声器的低中频消声性能，但插入障板的位置对阻性和抗性消声器的影响规律不同，障板均等划分对阻性消声器的传递损失增大有利，对抗性消声器则并不一定.

3) 多腔室消声器腔室间距对传递损失的影响主要体现在峰值数目上，峰值大小基本不变，总体而言，腔室间距为0时，消声器在全频段具有最好的消声性能.

[1]SULLIVAN J W, CROCKER M J. Analysis of concentric tube resonators having unpartitioned cavities[J]. Journal of the Acoustical Society of America, 1978,64(1):207-215.

[2]WANG C N. Numerical decoupling analysis of a resonator with absorbent material[J]. Applied Acoustics, 1999,58:109-122.

[3]SELAMET A, XU M B, LEE I J, et al. Analytical approach for sound attenuation in perforated dissipative silencers[J]. Journal of the Acoustical Society of America,2004,115(5)：2091-2099.

[4]SELAMET A, LEE I J， HUFF N T.Acoustic attenuation of hybrid silencers[J]. Journal of Sound and Vibration, 2003,262:509-527.

[5]JI Z L, SELAMET A. Boundary element analysis of three-pass perforated duct mufflers[J]. Noise Control Engineering Journal, 2000,48:151-156.

[6]季振林.穿孔管阻性消声器消声性能计算及分析[J].振动工程学报,2005,18(4):453-457.

[7]徐贝贝，季振林.穿孔管消声器声学性能的有限元分析[J].振动与冲击,2009,28(9):112-115.

[8]黄其柏.考虑非均匀流场的管道声学理论及消声器研究[J].华中理工大学学报,1999,27(8):46-48.

[9]袁守利，武明飞，刘志恩.考虑温度场影响的排气消声器性能仿真优化[J].武汉理工大学学报：信息与管理工程版,2014,36(5):627-635.

[10]李增刚，詹福良.Virtual. Lab Acoustics声学仿真计算高级应用实例[M].北京:国防工业出版社,2010.

[11]MELLING T H. The acoustic impedance of perforates at medium and high sound pressure levels[J]. Journal of Sound and Vibration, 1973,29:1-65.

[12]JI Z. Acoustic attenuation performance of a multi-chamber muffler with selective sound-absorbing material placement[C]. SAE International, 2007：202-213.

[13]LEE I. Acoustic characteristics of perforated dissipative and hybrid silencers[D].Ohio：The Ohio State University, 2005.

Analysis of Acoustic Attenuation Performance of Multi-chamber Perforated Mufflers

ZHENG Han1)ZHOU Qidou1)MAO Yanlei2)

(DepartmentofNavalArchitectureEngineering,NavalUniversityofEngineering,Wuhan430033，China)1)(Department91206Army,Qingdao266108，China)2)

One-dimensional analytical method and three-dimensional finite element method were adopted to predict the acoustic attenuation performance of perforated mufflers. Comparisons with experimental results demonstrated that three-dimensional finite element method can predict the transmission loss accurately in the whole frequency band. The finite element method was then used to investigate the effects of chamber sequence, chamber number, chamber division and chamber distance on the acoustic performance of multi-chamber perforated mufflers. The results show that the transmission loss of a multi-chamber perforated muffler is the sum of all component single-chamber mufflers’ transmission loss. The chamber sequence has no impact on the transmission loss. It can greatly improve the acoustic attenuation performance to turn a one-chamber muffler into a multi-chamber muffler by inserting rigid baffles in the chamber. The location of baffles has definitely different effects on dissipative and reactive mufflers. Making one chamber into two equal chambers is good for dissipative mufflers on increasing the transmission loss, which is not true for reactive mufflers. The distance between two chambers has influence on the number of peaks of transmission loss curves, and no influence on the peak values. In general, when the distance is zero, the muffler has the best acoustic performance.

perforated muffler； multiple chambers； transmission loss； finite element method

2015-05-30

TB535.2

10.3963/j.issn.2095-3844.2015.04.023

郑 晗(1988- )：男，博士生，主要研究领域为噪声与振动控制