植物冠层结构参数测量中存在的问题及对策

闫 贺 ，张天安，刘应安

（南京林业大学 信 息科学技术学院，江苏 南 京210037）

1 引言

植物冠层是植物与外界发生相互作用的主要场所，植物的许多生化物理过程都发生在冠层。冠层结构参数是用来反映植物生长状况的重要指标。在诸多冠层结构参数中，叶面积指数反映了单位地表上植物叶片面积的多少。而平均叶倾角表达了冠层中叶片的空间取向。这些冠层结构参数决定了植物管理光能和水分的能力。传统的冠层结构参数测量方法是手动测量。手动测量法原理简单，但需耗费大量时间和人力，测量时还会破坏植物，所以并不适用。半球摄影法是一种测量冠层结构参数的快速可靠的新方法，它用有鱼眼镜头的数码照相机摄取冠层影像，从而研究植被的冠层结构。半球摄影法没有破坏性、可重复采样、获取庞大的数据、操作简单快捷且结果准确，目前在生态学、森林培育学等学科上获得了一定的应用，但在获取植物冠层结构参数方面的应用还并不多见。

2 植物冠层结构参数测量研究现状

叶面积指数是分析植物群体和群落生长的一个重要参数，自1947年被提出以来，叶面积指数已成为一个非常重要的植物学参数和评价指标，并得到了广泛应用。近年来，学者们［1～3］越来越重视通过遥感反演计算叶面积指数，但在很大程度上，遥感反演计算叶面积指数的精度会受地面叶面积指数测量精度的影响。叶面积指数的测量方法主要有两大类：直接接触法和间接非接触法。直接法耗时耗力且会对植被造成破坏；间接法方便无破坏性，但测量结果有偏差。

现有的测量方法复杂且不精确，国内外学者为了获得更有效可靠的实验数据，进行了大量的研究［4，5］。文献［6］研究了基于Beer－Lambert定律对叶面积指数的测量，指出其中存在严重的低估问题，该方法对于测量叶面积指数有较大局限性，间接测量叶面积指数需要进一步地深入研究。文献［7］针对叶面积指数的测量值比真实值稍小的问题，研究了有效叶面积指数和真实叶面积指数并建立出二者之间的线性模型。新型的三维点云技术能准确获取冠层结构，文献［8］基于三维点云对树木测定因子进行测定并计算叶面积指数。

3 植物冠层结构参数测量中存在的问题及对策

3.1 基于半球摄影法的孔隙度提取

装备鱼眼镜头的数码照相机拍摄得到的彩色图像为原始数据。这些数据经过处理，转化为只含有“树叶”和“背景”两种元素的二值图像，用来提取孔隙度数据并计算冠层参数。冠层孔隙度是太阳光穿过冠层不被截获的概率，孔隙度是关于入射光角度的函数，在同一冠层中，不同的入射角有对应的孔隙度。可以认为在同一冠层，孔隙度只与入射光天顶角有关。

半球冠层图像分析中，要将图像分为n个同心环，得到n个对应相应视角的孔隙度。n取值越小，视角的分辨率越小，要处理的数据也相应较少，但会使孔隙度数据有较大的变化，曲线抖动厉害。n取值越大，分辨率越大，提取的孔隙度数据变多，曲线更光滑，但是要处理的数据会更多，处理速度会降低。虽然n取值越大能得到更详细的孔隙度，但要耗费更多的时间，所以需要在计算效率和计算精度之间获得平衡。

3.2 冠层参数研究的相关理论

3.2.1 Beer－Lambert定律

Beer－Lambert定律，也称光的吸收定律，开始用来测量可见光通过植被冠层时被吸收的情况，Monsi and Seaki（1953）用该定律来模拟光线被植被冠层吸收，得到半球摄影法冠层结构参数的常用等式：

3.2.2 叶倾角分布函数

冠层孔隙度与叶面积指数和叶倾角分布有关。常见植物的叶倾角分布一般可分为五种：水平分布、垂直分布、锥面分布、球面分布和椭球面分布。其中，椭球面叶倾角分布可以视作一般形式，其他四种可以认为是特殊形式。

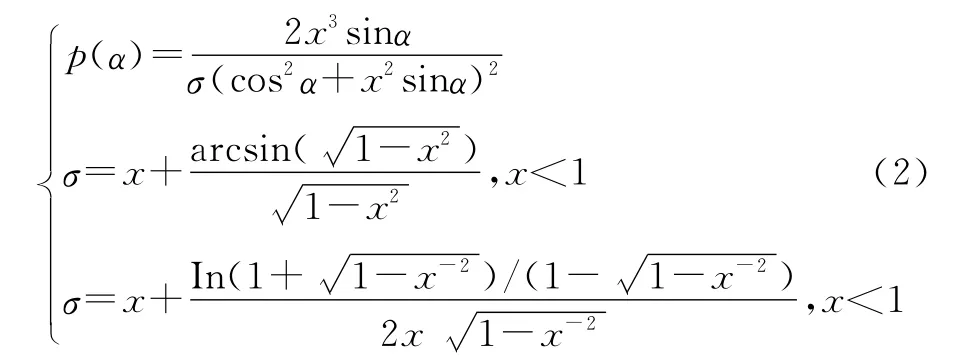
椭球函数模型表述为：

上式中，p（α）为叶倾角密度函数，表示叶倾角α为的叶片总面积占整个冠层面积的比值，x是椭球水平与垂直半轴的比值，x越大表示冠层叶倾角越接近水平分布，x越小表示叶倾角越接近垂直分布。

A：上海是近代中国印刷业的发祥地，可追溯至1843年，英国传教士建立墨海书馆。上世纪50年代后期，国家出台政策，计划推动印刷业的合理布局与发展，在此大背景下，印刷业相对发达的上海开始向全国输出资源。当时上海有30多家以出版物印刷为主营业务的印刷企业，他们向全国22个省市输出技术人才，援建内地印刷业。据不完全统计，输出的这部分技术人员有2000多名。1978年，上海印刷业的销售收入大概是5亿元，到2017年底，销售收入已经达971亿元。数字的比对简单、直观，单从规模上讲，这也是上海印刷业飞跃发展的一个表现。

对叶倾角密度函数有：

另外，x与平均叶倾角关系为：

3.3 叶面积指数（LAI）和平均叶倾角的研究

在半球冠层图像分析中，分成的同心环越多，视角范围越小，得到的孔隙度数据会具有较高的偶然性。但是通过多次试验取平均值，可以有效减小偶然因素对实验带来的影响。

3.3.1 Miller公式法

基于 Miller积分公式（Miller，1967），Chen和Blaek（1991）假定冠层孔隙度只与入射角（视角）有关，并推导了使用冠层孔隙度数据积分求LAI的公式：

3.3.2 迭代反演法

同时含有LAI和平均叶倾角的方程如下式：

上式中，L＾AI是最优叶面积指数是最优平均叶倾角，T（θ）为实测冠层孔隙度，Tsim（θ）为模拟的孔隙度，按式（6）展开。

本研究对6张彩色数字图片进行分析，分别采用Miller公式法和迭代反演法获取的冠层参数见表1。

研究发现，Miller公式法的缺点在于以下方面。

（1）Miller公式法认为冠层孔隙度只与视角有关，但忽略了叶倾角对孔隙度的影响。对叶倾角为球状分布（平均叶倾角为57°左右）的冠层，结果比较准确；但是对冠层叶倾角非球状分布（如水稻等）的冠层，结果的准确度则相对较低。

表1 叶面积指数和平均叶倾角结果数据

（2）半球摄影法从图像上很难获得全角度的孔隙度。当视角很大时，入射光线与地面几乎水平，穿越冠层的路径长度近似于无穷大，受地形和光线等因素影响严重而不易获得准确的孔隙度。

与Miller公式法一样，迭代反演法也使用了全视角的孔隙度数据。迭代反演法相对Miller公式法更加优越，因为它在计算叶面积指数的同时也考虑了叶倾角分布的影响，所以可以同时得到叶面积指数与平均叶倾角这两个参数。但是，迭代反演法容易被极端值所影响。从半球图像上获取的孔隙度数据经常出现极端值，尤其在视角比较接近90°的情况下（图像边缘区域），孔隙度往往很小，甚至会是0；相反，在视角接近0°的情况（图像的中心），孔隙度常常是1。这些极端值往往会干扰迭代反演法的准确度。此外，迭代反演法需要很大的计算机资源，运算效率比其他方法低，尤其是视角分辨率相对较高时（图像划分的同心环较多），运算时间偏长，不利于实时数据的获取。

3.4 基于激光点云数据的实验

对本研究获取的激光点云数据枝干分离后投影到半径固定的球上，如图1（a）；投影到平面上，划分为9个同心环，如图1（b）。得到6组孔隙度和视角函数图，如图2。

图1 激光点云实验

对叶片数据计算可得平均叶倾角，得到平均叶倾角后，根据式（2）、（4）可以得到叶倾角密度函数，如图3所示。根据式（1）、（4）可以算得叶面积指数LAI和视角的关系函数图像，如图4所示。

4 结语

随着科学技术的迅猛发展，运用半球摄影法和三维点云技术获取林分冠层的相关数据，对鱼目图像和三维点云数据进行分割，计算林分冠层结构参数，其准确度和精度也较高。今后可以尝试其他方法，做进一步的研究。

图2 点云数据不同n取值下孔隙度和视角函数

图3 叶倾角密度函数曲线

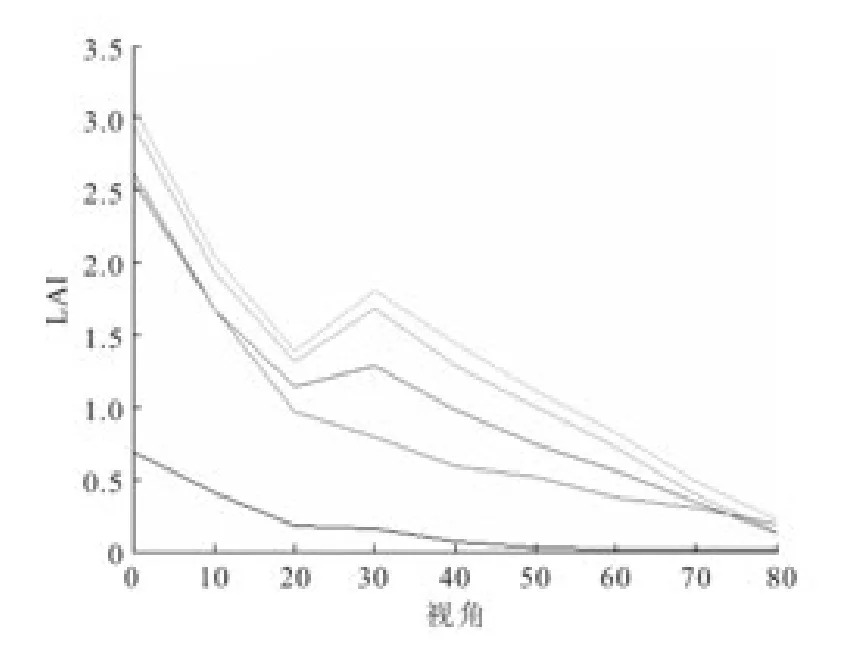
图4 六组数据LAI和视角函数

［1］徐希孺，范闻捷，陶 欣.遥感反演连续植被叶面积指数的空间尺度效应［J］.中国科学（D辑：地球科学），2009，39（1）：79～87.

［2］刘 洋，刘荣高，刘斯亮，等.基于物理模型训练神经网络的作物叶面积指数遥感反演研究［J］.地球信息科学学报，2010，12（3）：426～435.

［3］江 东，付晶莹，黄耀欢，等.地表环境参数时间序列重构的方法与应用分析［J］.地球信息科学学报，2011，13（4）：439～446.

［4］吴伟斌，洪添胜，王锡平，等.叶面积指数地面测量方法的研究进展［J］.华中农业大学学报：自然科学版，2007，26（2）：270～275.

［5］de JesusW C Jr，do Vake F C R，do Resende C R，et al.Comparison of two methods for estimating leaf area index on common bean［J］.Agronomy Journal，2001（93）：989～991.

［6］杜春雨，范文义.有效叶面积指数与真实叶面积指数的模型转换［J］.东北林业大学学报，2010，38（7）：126～128.

［7］胡容海，阎广建.对Beer－Lambert定律间接测量森林LAI的误差低估分析［J］.地球信息科学学报，2012，14（3）：366～375.

［8］高绍伟，冯仲科，吴露露.基于点云数据的测树因子提取与分析研究［J］.林业资源管理，2012（6）：101～104.