非正交轴系激光经纬仪测量技术研究
吴 斌,杨 松
(天津大学精密测试技术及仪器国家重点实验室,天津300072)
引 言
随着航空(大型客机及运输机等)、航天(火箭、卫星、飞船及空间站等)、电力(大型火电、水电及核电机组等)、轨道交通(高铁、地铁及城市轨道车辆等)、汽车、船舶(航空母舰、大型客轮、油轮等)、工程机械(隧道挖掘和盾构机、浮式起重机等)、重型机械(800MN大型模锻压机等)以及大型通讯设备(探月工程50m,66m口径地面天线等)等国家重大技术装备制造业水平的提高,在大尺寸范围内对单点坐标、几何尺寸及曲面特征等的现场、快速、精密测量已成为工业测量的研究热点和难点。目前,激光跟踪仪、全站仪、经纬仪和摄影测量相关设备是实现大空间、大尺寸对象精密制造、装调的主要测量手段。激光跟踪仪和全站仪测量时需要合作目标(靶镜),摄影测量设备往往需要人工粘贴标记,都无法实现测量自动化,而新型激光电子经纬仪(Leica TM5100A/TM6100A)由于具备伺服驱动和激光瞄准等功能,为实现自动化测量提供了新的途径[1]。
为满足船舶分段的自动化测量需要,作者[2]曾研究了以两台Leica TM5100A激光电子伺服经纬仪为基础测量平台,结合与视准轴同轴投射的准直激光技术和视觉跟踪引导技术,构建了一套面向大空间、大尺寸对象现场自动测量的系统样机。该系统在传统经纬仪测量方法的基础上引入了视觉测量的原理机制,利用多分辨率视觉成像方法对被测区域进行扫描监测,对被测目标进行自动识别、匹配和跟踪瞄准,通过计算被测点成像位置信息控制伺服马达驱动的高精度电子经纬仪进行被测点的空间方位角度测量,再由多台经纬仪交会实现大空间范围内点坐标的测量。但在后续研究和应用的过程中发现,高精度电子经纬仪对制造工艺要求严格、造价昂贵,制约了其应用推广。
系统成本主要来自于经纬仪。对于传统经纬仪而言,三轴正交(即垂直轴与水平轴正交,水平轴与视准轴正交,且三轴交于一点)是实现精确角度测量对仪器本身的结构要求,若不能满足,则会产生水平轴倾斜误差、垂直轴倾斜误差及视准轴误差,从而影响角度测量的准确性[3]。虽然上述误差可以进行补偿,但补偿范围有限。因此,为满足三轴正交的结构要求,在仪器的设计、加工、装配、检校和维护等方面有严格的要求,从而决定了该仪器制造和维护的高成本。
作者拟借鉴经纬仪的三轴结构模式,但突破传统经纬仪三轴正交的结构要求,提出并研究一种新的非正交轴系激光经纬仪架构及其测量原理与方法[4-5]。为大空间、大尺寸对象精密、自动测量提供新的理论支持和更为合理、有效的技术手段与装置。
1 非正交轴系激光经纬仪的架构
从组成部件来看,与传统经纬仪相比,非正交轴系激光经纬仪有类似的水平度盘和竖直度盘,不同之处是采用准直激光器代替了传统的望远镜。相应地,也存在3个轴:水平度盘旋转中心轴线、竖直度盘旋转中心轴线及准直激光束。借鉴传统经纬仪的三轴概念,将其三轴也分别称为:竖直轴、横轴和视准轴,但竖直轴与横轴、横轴与视准轴均无正交要求,且三轴也无需交于一点,因此称之为非正交轴系。由于竖直轴仅表示水平度盘的旋转中心轴线,不要求与大地的垂直关系,因此非正交轴系激光经纬仪在使用时无需整平。视准轴由一准直激光束标识,将传统不可见的望远镜光轴进行了可视化,多台仪器测量时,在被测特征处激光光斑的重合则标志着视准轴的空间交会。同样,参照传统经纬仪中的相关概念,将非正交轴系激光经纬仪围绕竖直轴旋转时,水平度盘提供的角度称为水平角,围绕横轴旋转时,竖直度盘提供的角度称为竖直角。但此水平角和竖直角,与传统正交轴系经纬仪的水平角和竖直角意义完全不同。传统经纬仪与非正交轴系激光经纬仪架构如图1所示。图中,1为竖直轴,2为安放平台,3为水平度盘,4为横轴,5为竖直度盘,6为视准轴。
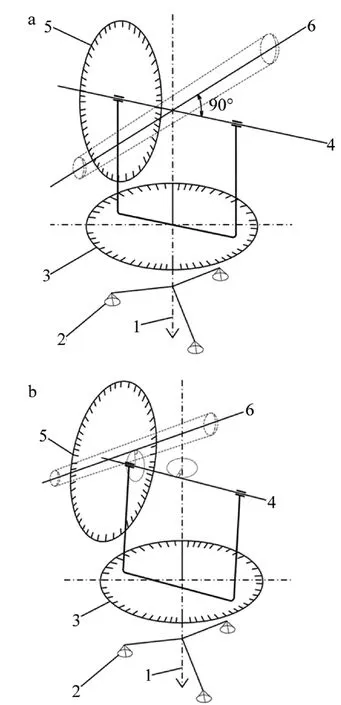
Fig.1 a—architecture of traditional theodolites b—architecture of non-orthogonal shafting laser theodolites
上述非正交轴系架构中,竖直轴、横轴和视准轴三轴无正交结构要求,也无需交于空间一点,因此,大大降低了对轴系设计、加工、装配和维护等方面的要求,降低了仪器制造成本。甚至由1维转台即可组装精密的经纬仪,极大地拓展经纬仪的应用领域,同时也发展了一种新的测量方法与技术。
2 测量原理和数学模型
2.1 测量原理

Fig.2 Schematic diagram of measurement system of non-orthogonal shafting laser theodolites
非正交轴系激光经纬仪的水平角和竖直角虽然与传统正交轴系经纬仪的水平角和竖直角意义不同,但由水平角和竖直角同样确定了非正交轴系激光经纬仪的视准轴的空间方位,因此,基于两台或以上非正交轴系激光经纬仪的视准轴空间交会[6]也可实现空间坐标的测量。如图2所示,准直激光光束即为可视化的视准轴,两激光束在被测点处所形成光斑的重合即表示视准轴的空间交会。
2.2 非正交轴系激光经纬仪数学模型
根据图1所示的非正交轴系激光经纬仪架构及2维云台运动轨迹[7],以测站1为例,建立如图3所示的非正交轴系激光经纬仪坐标系o1-x1-y1-z1。首先选取竖直轴上任意一点为坐标原点o1,定义竖直轴向下方向为y1轴,过o1点做o1y1的垂线并定义为o1x1,则o1z1轴满足右手法则。由于竖直轴即为y轴,故不存在传统意义上的竖直轴倾斜误差。

Fig.3 Sketch of coordinate system(o1-x1-y1-z1)
如图3所示,若用o'x'表示横轴,其中o'为横轴与竖直轴两异面直线的公垂线与横轴的交点,公垂线与竖直轴的交点用B表示。选取过o'点与o'x'轴垂直的任意直线为o'y'轴,满足右手法则建立竖直度盘的坐标系o'-x'-y'-z'。假设o'x'与o1y1轴的夹角为α1,公垂线的距离,o'B与o1x1轴的夹角为β1。根据几何关系,可以得到:

测量时,横轴o'x'以B点为中心围绕竖直轴o1y1旋转。如果得到固定距离r1和R1,固定角度α1和动态角度β1,便可以通过(1)式得到横轴o'x'在坐标系o1-x1-y1-z1中的实时方程。得出横轴的直线方程后,则可以通过上述方法建立动态测量坐标系o'-x'-y'-z',如图4所示。其中o'-x'-y'-z'可由o1-x1-y1-z1旋转平移得到。

Fig.4 Sketch of dynamic coordinate system(o'-x'-y'-z')
如图4所示,用MN表示视准轴,C为视准轴与横轴两异面直线的公垂线与视准轴的交点,公垂线与横轴的交点用D表示。假设MN与o'x'轴的夹角为γ1,公垂线的距离,CD与o'y'轴的夹角为δ1。根据几何关系,可以得到:

测量时,视准轴MN以D点为中心围绕横轴o'x'旋转。如果得到固定距离r1'和R1',固定角度γ1和动态角度δ1,便可以通过(2)式得到视准轴MN在动态坐标系o'-x'-y'-z'中的实时方程。根据横轴的实时方程,可以得到由o1-x1-y1-z1到o'-x'-y'-z'的矩阵Mr。最终,可以得到视准轴MN在坐标系o1-x1-y1-z1中的实时方程。坐标系o1-x1-y1-z1与o'-x'-y'-z'的关系如下所示:

其中,

2.3 测量系统数学模型
由前述内容可知,采用两台或多台非正交轴系激光经纬仪,基于其视准轴的空间交会可以实现空间点的坐标测量。在得到了非正交轴系激光经纬仪的视准轴动态方程的基础上,若能够建立起非正交轴系激光经纬仪坐标系之间的关系,则可将其视准轴的动态方程统一到一个坐标系下,从而联立求解出交会空间点的坐标。如图5所示,在借鉴视觉测量技术中的双目测量模型的基础上[8],建立了非正交轴系激光经纬仪的测量系统模型。测站1中,o1'为视准轴o1'P与z1=0平面的交点,建立动态测量坐标系o1'-x1'-y1'-z1',图像坐标系为O1-X1-Y1,焦距为1mm;测站2中,or'为视准轴or'P与zr=0平面的交点,建立动态测量坐标系or'-xr'-yr'-zr',图像坐标系为Or-Xr-Yr,焦距为1mm。

Fig.5 Measurement system model of non-orthogonal shafting laser theodolites
由摄像机透视变换模型[9-10]可以得到:

式中,s1代表图像坐标系O1-X1-Y1与动态坐标系o1'-x1'-y1'-z1'的比例关系,sr代表图像坐标系Or-Xr-Yr与动态坐标系or'-xr'-yr'-zr'的比例关系。
测站1中动态测量坐标系o1'-x1'-y1'-z1'可由坐标系o1-x1-y1-z1平移得到,它们的关系如下式所示:

测站2中动态测量坐标系or'-xr'-yr'-zr'可由坐标系or-xr-yr-zr平移得到,它们的关系如下式所示:

在非正交轴系激光经纬仪测量系统模型中,坐标系o1-x1-y1-z1与坐标系or-xr-yr-zr的位置关系固定不变。它们的关系如下式所示:

式中,M1r为测站1与测站r之间的矩阵,M1r矩阵分为旋转矩阵和平移矩阵,R1r为其中的旋转矩阵。
联系(5)式~(12)式,可以得到测站1中图像坐标系O1-X1-Y1与测站2中图像坐标系Or-Xr-Yr的转换关系,如下式所示:

于是,在坐标系o1-x1-y1-z1中空间3维点坐标可以表示为:

根据非正交轴系激光经纬仪测量系统模型,已知空间点在测站1、2中的图像坐标[11-12],只要求出M1r中的旋转和平移因子,可以被测点在坐标系o1-x1-y1-z1中的空间坐标。由(15)式得到:
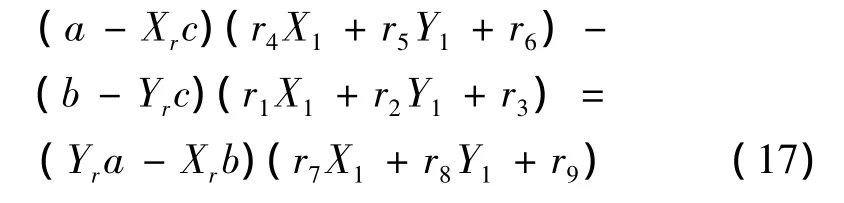
(17)式是一个含有12个参量的非线性方程,用函数f(x)=0 来表示,其中参量 x=(tx,ty,tz,r1,r2,r3,r4,r5,r6,r7,r8,r9)。由于旋转矩阵 R1r是正交的,具有6个正交约束条件。由此构成如下罚函数:

式中,M1~M6为罚因子,从而由被测点得到无约束最优化目标函数为:

对空间若干点进行测量,当测点数n≥6时,利用高斯-牛顿法[13]可以求解出矩阵M1r中的参量值,即可知测站1坐标系o1-x1-y1-z1与测站2坐标系or-xr-yr-zr之间的位置关系。此时将测站1坐标系作为整个测量系统坐标系,将两条视准轴方程统一到测站1坐标系o1-x1-y1-z1下,视准轴相交从而求得被测点坐标值。
3 模型仿真与实验验证
3.1 模型仿真
为了验证数学模型的正确性,采用基于SOLIDWORKS与MATLAB的相结合的方法进行仿真。首先,根据建立的数学模型在SOLIDWORKS中进行坐标系实体构造并根据各构件连接关系建立装配实体,如图6所示。然后,从装配实体中计算出需要的参量α,γ,r,R等。最后,根据水平度盘转角和竖直度盘转角,分别得出横轴、视准轴、被测点的仿真数据。
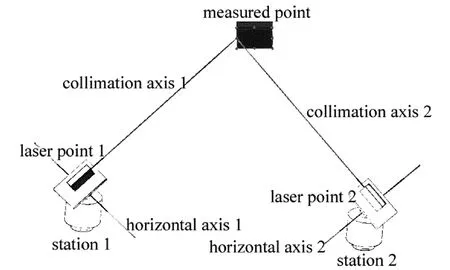
Fig.6 Simulation structure of measurement model
根据构建的测量模型,得到参量 α1=α2=92°,γ1=γ2=80°,r1=r1'=r2=r2'=6.911mm,R1=R1'=R2=R2'=-6.911mm,测站1与测站2间转换矩阵M1r如下:

改变模型中被测点的位置,求得相应的水平转角和竖直转角。通过数学模型,计算出被测点坐标(xs,ys,zs),与直接从装配实体得到的理论值(xt,yt,zt)进行比较。结果如表1所示。表1中的仿真结果验证了数学模型的正确性。
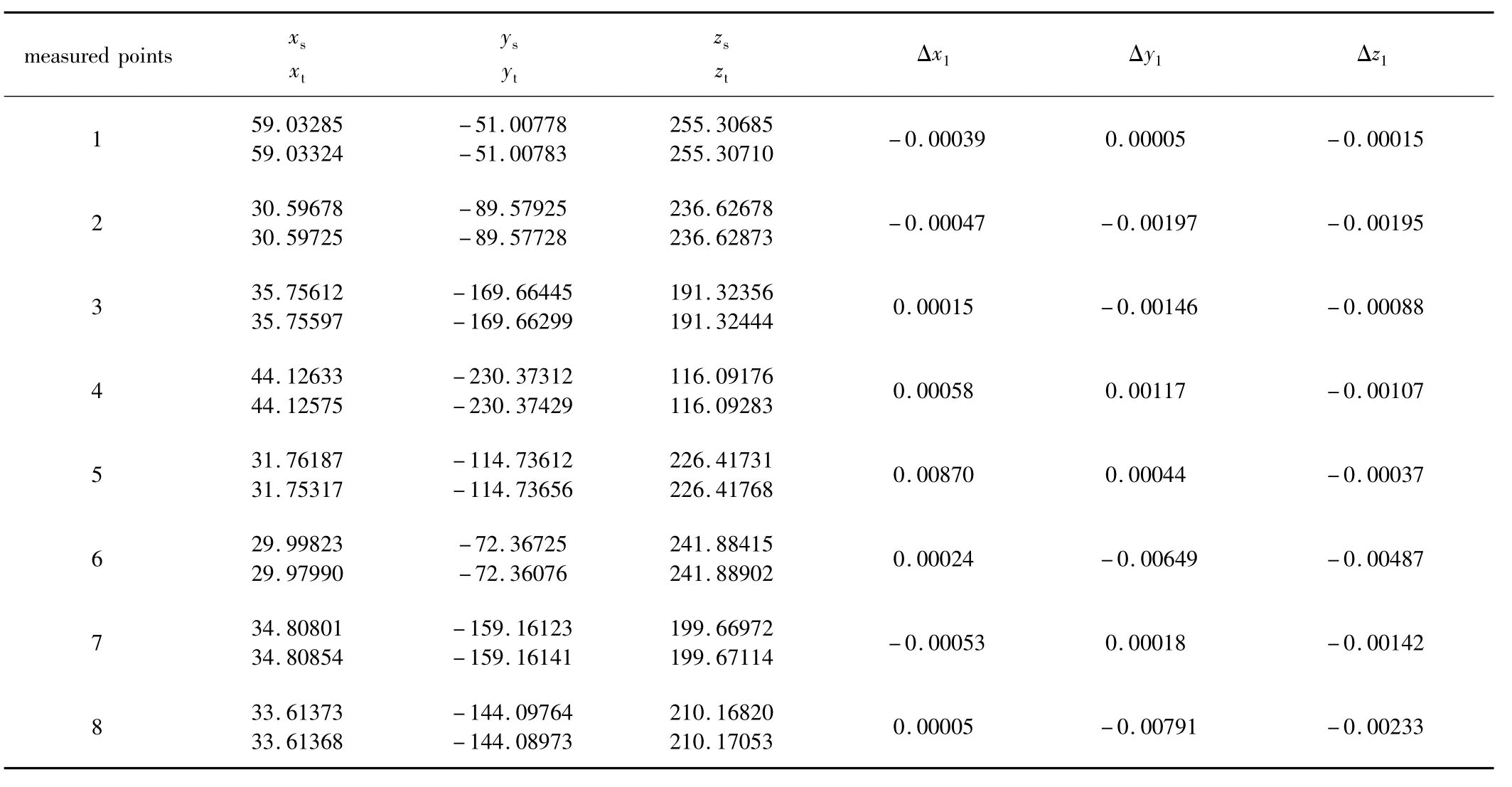
Table 1 Difference between the simulation values and the theoretical values/mm
3.2 实验验证
在上述的测量模型中,需要对2维云台的一些参量进行提前标定。标定后,便可以通过测站1和测站2的水平角∠H和竖直角∠V得出视准轴方程,实现对被测点的测量。
以测站1为例,首先是坐标系o1-x1-y1-z1的建立。2维数字云台由水平转台和竖直旋转平台组成。竖直旋转平台安放在水平转台上,而激光器安放在竖直旋转平台上。固定ZrO2陶瓷球(直径2mm,精密等级G10,GB308-2002/ISO3290-1998)到水平转台上,控制2维云台水平旋转,使用Leica公司的激光跟踪仪测量不同旋转角时陶瓷球坐标。保持云台在水平方向上固定,拟合出旋转圆的圆心o1以及旋转轴线的方向向量,旋转轴线即为竖直轴o1y1。圆心o1与陶瓷球初始位置的连线设为o1x1轴。通过右手法则,确定出o1z1轴,坐标系o1-x1-y1-z1建立完毕。
然后,利用相同方法,拟合出俯仰旋转轴的圆心o'和旋转轴线的方向向量,旋转轴线即为横轴o'x'。根据轴线o'x'与o1y1的解析式,计算出点o'和B的坐标,以及轴线Bo'的解析式。根据以上条件,可以得到横轴与竖直轴的固定夹角α1,Bo'与o1x1轴的夹角β1,横轴与竖直轴的固定距离r1,垂足B与轴心o1的固定距离R1。当云台旋转时,可以得出横轴o'x'在坐标系o1-x1-y1-z1的解析式。
最后,根据横轴o'x'在坐标系o1-x1-y1-z1的实时方程,解算出坐标系o1-x1-y1-z1到动态坐标系o'-x'-y'-z'的矩阵Mr,并建立坐标系o'-x'-y'-z'。在坐标系o'-x'-y'-z'中,视准轴MN用准直激光束表示,其方程可通过测量激光束上的多点得到。根据以上条件,可以得到视准轴与横轴轴的固定夹角γ1,DC与o'y'轴的夹角δ1,视准轴与横轴的固定距离r1',垂足D与轴心o'的固定距离R1'。
在参量标定完成之后,便可以通过建立的测量模型求解出被测点的坐标。
搭建的测量系统如图7所示,主要由点激光器、高精度数字转台及PC机等组成,转台采用步进电机驱动,分辨率为 0.0125°。

Fig.7 Measurement system of non-orthogonal shafting laser theodolites
通过计算,得到实验参量:α1=90.096546°,α2=88.904518°,γ1=92.490204°,γ2=89.370728°,r1=7.654343mm,r1'=108.755302mm,R1= -26.161574mm,R1'=11.211615mm,r2=6.399854mm,r2'=100.909601mm,R2= -30.206666mm,R2'=7.340672mm。测量空间中的多个点,利用高斯-牛顿法求解的测站1与测站2间转换矩阵M1r如下式所示。

Table 2 Difference between the measured values and the standard values/mm

对目标点进行测量,把解算出的结果(xe,ye,ze)与激光跟踪仪测得的标准值(xl,yl,zl)进行比对,其结果如表2所示。
由以上实验数据可以看出,本系统成功地实现了对空间点3维坐标的测量。但由于云台分辨率较低,引起了了较大的测量误差。如当测量半径R=5m时,云台导致的最大测量误差为δ=2πR×0.0125/360=1.09028mm,且此误差随着测量半径的变大而变大。在实验中,测量半径为3m,被测点在拉依达准则下的测量不确定度达到±1mm以内,系统能满足某些大尺寸测量场合的需要。
4 结论
针对大空间、大尺寸测量,在传统经纬仪测量系统的基础上,提出了一种新型的基于非正交轴系的激光经纬仪测量系统模型。该测量模型利用多台激光经纬仪视准轴空间交汇,实现了对空间点3维坐标的测量。在测量半径为3m时,被测点在拉依达准则下的测量不确定度达到±1mm以内,但测量不确定度会随测量半径的变大而变大。它克服传统经纬仪正交轴系的结构要求、降低了系统成本、减少了误差来源。但系统的精度还有待提高,需进一步优化测量模型;且测量过程完全手动,瞄准过程靠人眼,应提高自动化程度,以满足工业现场大尺寸高精度快速测量的需要。
[1] ZHANG Z L,ZHU J G,GENG N,et al.The design of double-theodolite 3-D coordinate measurement system[J].Chinese Journal of Sensors and Actuators,2010,23(5):660-664(in Chinese).
[2] WU B,WANG B.Automatic measurement in large-scale space with the laser theodolite and vision guiding technology[J].Advances in Mechanical Engineering,2013,2013:629385.
[3] TIAN L D,LIU C H,ZHAO J K,et al.Impact of three-axis error on angle measurement of photoelectric theodolite[J].Infrared and Laser Engineering,2013,42(1):193-195(in Chinese).
[4] LI G Y.Principle and development trend of non-orthogonal coordinate system[J].Journal of Geomatics,2003,28(1):4-10(in Chinese).
[5] HUANG G Y,LI G Y.Study of system orientation and coordinate calculation of IMS[J].Acta Geodaetica Et Cartocgraphica Sinica,2003,32(3):256-260(in Chinese).
[6] ZHOU H,ZHU J G,YE S H.The vision-based automatic collimation methodology of electronic laser theodolites for spatial coordinate[J].Chinese Journal of Sensors and Actuators,2011,24(8):1205-1207(in Chinese).
[7] GUO J Z.Research on high-precision 2-D turntable based on optical gratings[D].Beijing:North China University of Technology,2013:2-10(in Chinese).
[8] ZHANG X P,WANG J Q,ZHANG Y X,et al.Large-scale three-dimensional stereo vision geometric measurement system[J].Acta Optica Sinica,2012,32(3):0315002(in Chinese).
[9] ZHANG Z L,ZHU J G,YE S H,et al.The guidance methodology of a new automatic guided laser theodolite system[J].Proceedings of the SPIE,2008,7160:806991.
[10] ZHOU H,ZHU J G,YE S H,et al.Resolution improvement of the electronic eheodolite in automatic guided laser theodolite system by subdivided locating method of image[J].Proceedings of the SPIE,2008,7160:807057.
[11] XIAO Z T,ZHANG W Y,GENG L,et al.Accuracy analysis of binocular vision system[J].Opto-Electronic Engineering,2014,41(2):6-8(in Chinese).
[12] ZHANG G J.Vision measurement[M].Beijing:Science Press,2008:134-166(in Chinese).
[13] SHANG C,WANG G Q,CHEN G L.Test method of the absolute angle measuring system with inductosyn based on theodolite[J].Chinese Journal of Sensors and Actuators,2008,21(5):865-868(in Chinese).

