基于改进遗传算法的矩形件下料优化方法研究*

□ 刘淑伟 □ 郭顺生 □ 郭 钧 □ 杜百岗 □ 李西兴

武汉理工大学机电工程学院 武汉 430070

随着我国科学技术的发展，机械制造加工业也快速发展，钢结构产品应用广泛，作为原材料钢材的消耗量日益增加。对于以钢结构产品为主要生产对象的建材装备企业来说，钢材的费用在生产成本中占了很大的比重，因此，企业在生产下料时，合理优化矩形件排样、提高板材利用率、降低生产加工成本是提升企业竞争力的重要方式之一。

矩形件优化排样问题是指在给定的矩形板材上，将一系列矩形零件以板材利用率最大为目标，按最优方式进行排布。针对该问题，近几十年来众多国内外学者对其展开研究并提出了多种合理的、有效的求解算法和模型[1-3]。由于搜索空间随问题规模的增大而急速增大，所以很多学者利用遗传算法作为基础算法并结合其它优化算法，构建组合算法来解决该问题模型。如文献[4]中结合启发式递归算法与遗传算法，文献[5]提出基于遗传算法的混合元启发式算法，文献[6]基于对传统遗传算法的改进，主要引入分阶段调整遗传算子的策略，文献[7]提出基于小生境技术的自适应遗传模拟退火算法。以上算法对传统的方法进行改进，在很多情况下可以得到较好的板材利用率和计算效率，但在实例应用中仍存在效果不佳的现象。

基于此，笔者采用基于遗传算法和最低水平线法相结合来求解矩形件优化排样问题，并引入不同阶段不同遗传算子，以避免在遗传算子操作过程中出现优良基因的缺失。

1 矩形件下料优化问题数学模型

1.1 问题描述

矩形件下料优化问题主要指以板材利用率最高作为目标函数，即在给定长、宽的矩形板材上以最优方式切割出所需矩形零件[8]。某钢结构产品需要n种同材质同厚度的矩形零件 Ri（i=1，2，...，n），其中矩形零件的面积表示为li×wi，每种零件所需个数为ai。现设定矩形板材的宽度为W，长度为L，同时Ri、Rj互不重叠，i≠j，i、j=1、2、...、n；Ri、Rj必须放在板材内。

1.2 数学模型

将所有矩形零件进行编码处理，形成编码集Ri、i∈N，N=｛1，2，...，n｝；L、W 为所用原材料的长度和宽度；li、wi为矩形件 Ri的长度和宽度；（xi、yi） 为 Ri的左下角点坐标；（xi′、yi′） 为 Ri的右上角点坐标；3 个二进制逻辑变量，ri=0或1，当零件Ri横放时取1，反之取0；lij=0 或 1，当零件 Ri置于 Rj左侧时取 1，反之取 0；bij=0或 1，当零件 Ri置于 Rj下侧时取 1，反之取 0；H为所利用矩形板材的最大高度；F为原材料的利用率。目标函数：

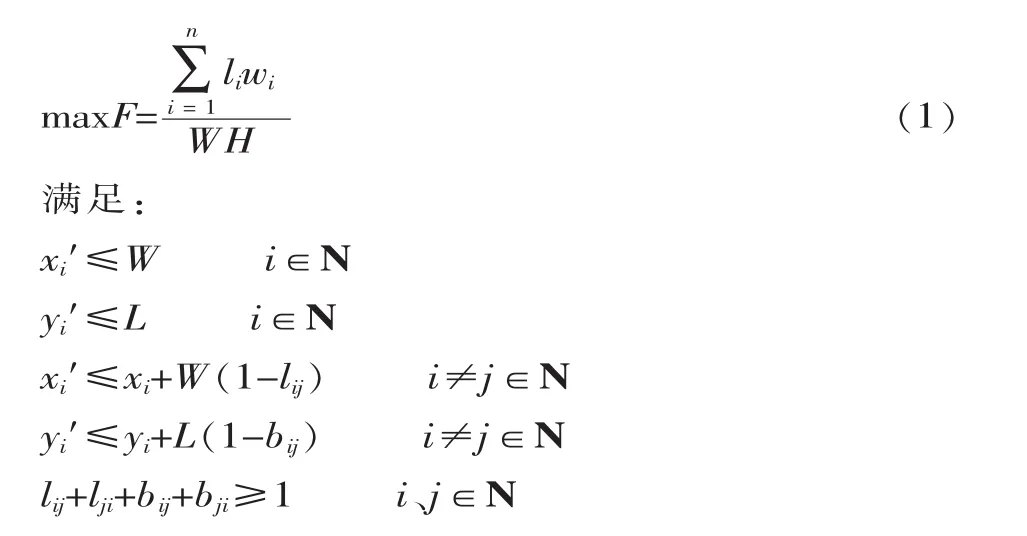
2 优化模型求解

2.1 遗传算法实现的基本要素

2.1.1 基因编码策略

采用十进制编码方法[9-10]，即将每一待排矩形零件进行整数编号，i=1、2、...、n，将 n 个 Ri的编号按照一定的顺序排列， 即构成一个个体 P=｛p1，p2，...，pn｝，1≤|pi|≤n，即问题的一个解。每个基因代表一个Ri，并有正负之分，正号表示Ri横放，即矩形零件的长度和板材的长度方向平行；负号则反之。如排列顺序为（5、-1、3、2、-4），则对应染色体为｛5，-1，3，2，-4｝，此序列表示首先排5号零件，零件横排；然后排1号零件，零件竖排；并以此类推，得到最终排样图。

2.1.2 初始化种群

在种群染色体初始化过程中，给定n个零件，随机产生 m 条染色体 p1、p2、...、pm构成初始种群，笔者采用MATLAB中的Randperm（）函数和Rand（）函数结合来产生随机序列，这样既可以产生负数序列，也可避免非法子串的产生。针对文中的条件，经过多次测验，在采用种群规模为40时，既能保证较高计算速率，也可以得到很好的板材利用率。

2.1.3 适应度函数

遗传算法中每个染色体质量的优劣是利用适应度函数进行评价的，染色体适应度值越大，则其质量越好。笔者主要考虑废料再利用来定义适应度函数F（P），即尽可能降低所需板材的最大高度，使其剩余原材料的高度仍在可利用范围之内，尽可能提高可再利用废料的利用率。

2.1.4 遗传算子

（1）选择算子。所采用的选择算子为随机联赛选择方法，即基于个体适应度值大小关系的选择方法，通过对个体间的交叉、变异等不断地产生新个体。虽然在这个过程中随着种群的进化会产生更多优良个体，但由于过程中选择、交叉、变异是随机的，会造成部分最优个体的破坏，使适应度值下降，对算法的运行效率和收敛性造成影响，所以笔者采用精英保留策略来设定选择算子。

（2）交叉算子。在遗传算法中，交叉算子主要产生新个体，并决定了遗传算法全局搜索的能力。采用顺序交叉操作产生新的个体，此方法可将父代的基因顺序重组，并且不会产生非法个体。以两个父代染色体为例进行交叉操作， 详细阐述顺序交叉操作，P1：｛4，-3，9，7，-2，6，-8，5，1｝，P2：｛-5，7，2，-6，4，9，1，-3，-8｝。 首先，在1-9之间随机产生两个交叉点，如交叉点为3和6， 将父代分为 3 个部分， 即 P1：｛4，-3，9|7，-2，6|-8，5，1｝和 P2：｛-5，7，2|-6，4，9|1，-3，-8｝，交叉点之间的中间段保持不变， 得到：P1：｛x，x，x|7，-2，6|x，x，x｝ 和 P2：｛x，x，x|-6，4，9|x，x，x｝。 然后，记取父个体 2 从第二个交叉点开始的矩形件序号排列顺序，当到达基因末尾时，返回染色体初始位置继续记录矩形件序号，直到第二个交叉点结束，这样便得到了父个体2从第二个交叉点开始的矩形件序号排列顺序为 （1、-3、-8、-5、7、2、-6、4、9）。 对于父个体 1 而言，已有零件 7、-2、6，将它们从父个体2的排列顺序中去掉，得到排列顺序（1、-3、-8、-5、4、9）， 再将这个排列顺序复制给父个体 1，复制的起点也是从第二个交叉点开始，从而得到子个体1对应的整数串，这样子个体1的排列顺序为C1=｛-5，4，9|7，-2，6|1，-3，-8｝，同样子个体 2 的排列顺序为：C2=｛-3，7，-2|-6，4，9|-8，5，1｝。

（3）变异算子。采用旋转变异，假设待排零件的总数为n，旋转变异操作是在[1，n]之间产生一个随机数b，将b位置上的零件序号转换为其相反数，即将横放矩形件转换为竖放。

2.1.5 终止准则

整个算法在解空间进行搜索的过程中呈现收敛的趋势，设定的终止准则为：设定期望的板材利用率，如果在求解过程中，达到了预先设定值，则算法终止；否则当遗传代数达到预先设定迭代次数值时，算法终止。整个运算过程中，适应度值最大的染色体所对应的排样方案即为矩形件下料优化的最优解。

2.2 基于最低水平线的搜索算法

在上述遗传算法运行的过程中，首先进行种群初始化，产生一系列整数串，然后对每个个体的适应度值进行评价，在评价时需要将最初产生的染色体，即一串基因编码，转化成板材上的矩形零件，从而形成排样图，得到矩形零件所占板材的总面积，再进行比较优化。为了实现这一转化，需要按照一定的启发式算法将矩形零件进行排列，如BL算法、下台阶算法、最低水平线算法。BL算法拥有一定的局限性且易出现板材左侧偏高的现象，而下台阶算法则容易导致板材右侧偏高，相比之下，最低水平线算法可以有效地解决以上两种算法存在的缺陷，在一定程度上实现板材利用率的提高[11]。但最低水平线法容易出现部分排样高度偏高情况，造成板材最低水平线以上板料的浪费[12]。因此，提出在算法处理时首先向后搜索，将后面未排零件中选取宽度小于或等于最低水平线宽度的零件，与当前零件互换并进行排放，将最低水平线搜索算法嵌套在遗传算法的适应度值函数中。设定最高轮廓线矩阵，记录每次排放矩形件时的最高轮廓线，在适应度函数中嵌套排样函数，当所有矩形零件按照排样函数排放完毕后，按照最高轮廓钱矩阵中记录的最大尺寸，即可求得板材的利用率。

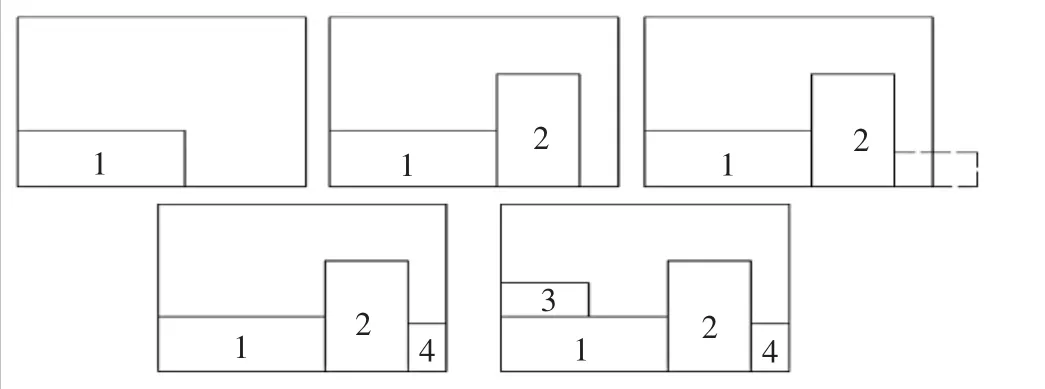
▲图1 基于最低水平线的搜索算法

对于给定排放序列（1，-2，3，-4｝的基于最低水平线搜索算法的排放过程如图1所示，排放结束后，序列更新为｛1，-2，-4，3｝。

2.3 算法流程图

结合上述遗传算法和基于最低水平线搜索算法的过程，其算法总流程图如图2所示，其中FP为设定的期望板材率用率，gen为迭代次数，Gen为设定的迭代次数。

3 计算实例

为了验证论文中所提出的矩形件下料优化算法的有效性，选取了某建材装备企业某生产部件所需的矩形零件进行排样计算。算法的参数设置为：种群规模Popsize=40，迭代次数Gen=200，交叉概率Pc=0.60，变异概率Pm=0.001。选取的排样板材的长度L=2 000 mm，板材的宽度W=1 500 mm，待排矩形零件的尺寸数据见表1。

在上述算法参数设置的前提下，将算法重复运行10次。在10次运算过程中，遗传算法所得到的排列顺序和排样图都不同，重复运行10次的板材利用率平均值为94.63%。在10次运算结果中，94.26%出现3次，94.02%出现2次，95.73%出现2次，95.48%出现2次，93.06%出现1次。由上述结果可知，板材利用率最高值为95.73%。虽然在运算过程中，板材利用率出现相同现象，但零件排放序列却是不同的。在实际应用算法运行时，可多次运行选取最优结果。

笔者选取了最优排样方案的收敛曲线和零件排放序列，板材利用率为95.73%，收敛曲线如图3所示。根据得到的最大板材利用率的排样顺序，对其进行自动排样，得到的排样图如图4所示。

4 结束语

表1 零件数据

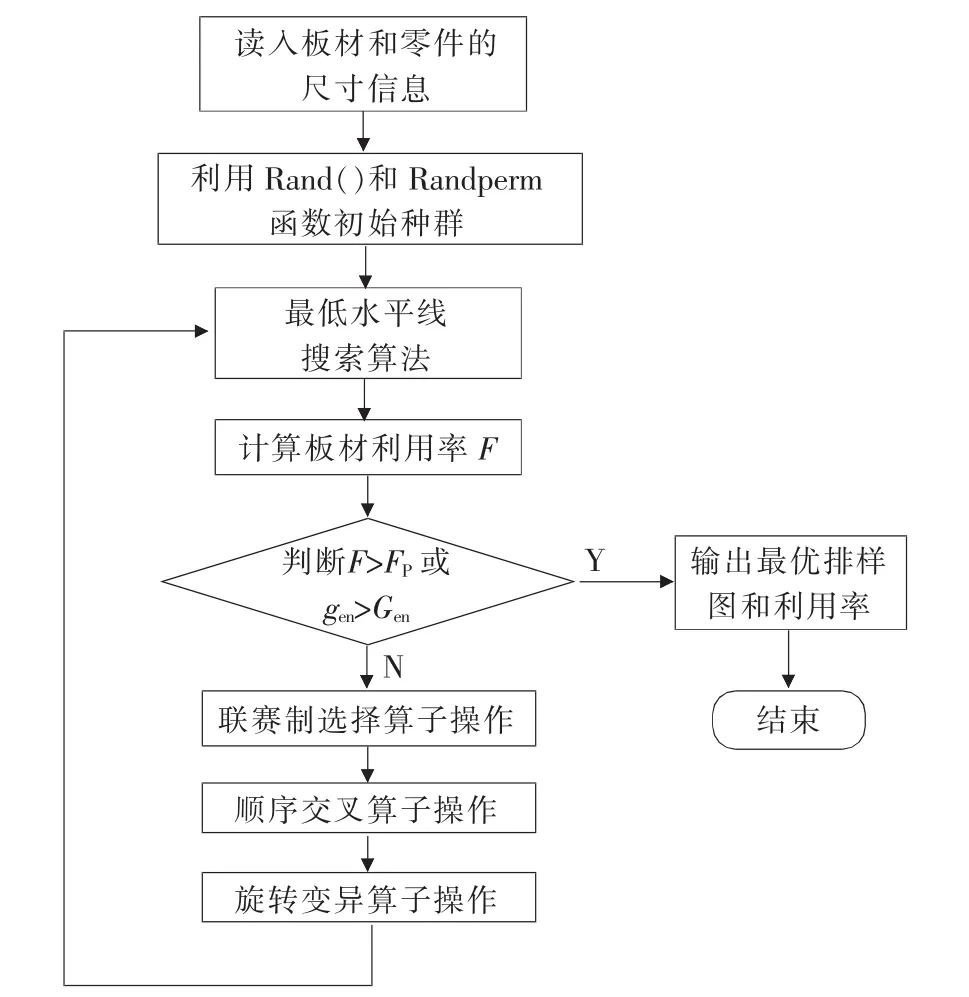
▲图2 算法流程图

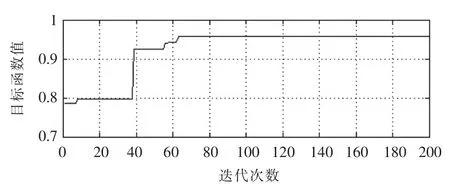
▲图3 板材利用率收敛曲线

笔者以企业钢结构件的下料过程为背景，建立矩形件下料优化数学模型，结合遗传算法和基于最低水平线的搜索算法，对矩形件下料优化数学模型进行求解，获得最优解，实现零件在原材料上的合理排样，降低板材的浪费，提高板材利用率。在遗传算法中，采用不同的合适的遗传算子操作相结合的方法，进行个体的选择、交叉和变异，在选择操作中采用精英保留策略以避免优秀个体的缺失，然后利用适应度函数对每代的每个个体进行适应度值计算，多次迭代，直到算法终止，得到个体最优排布和板材的利用率，并自动绘制板材的排样图。提出的算法可以有效地提高板材的利用率，降低板材的消耗和生产成本，显著提高企业的经济效益和竞争力，具有重要的利用价值。

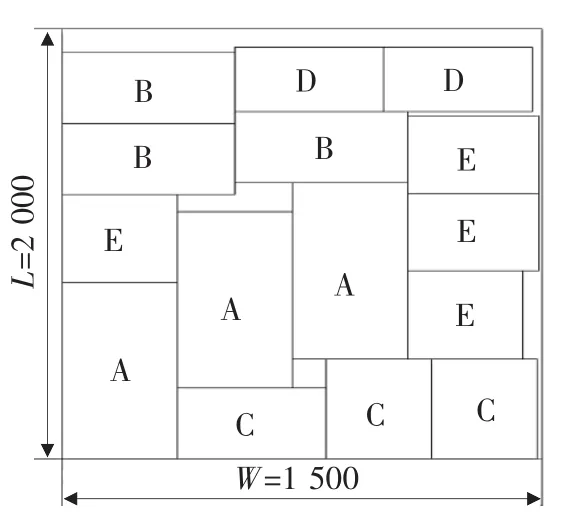
▲图4 优化下料

[1]童科，毛力.基于蚁群优化算法求解矩形件排样问题[J].计算机工程与科学，2011（7）：158-162.

[2]李波，王石，施松新，等.基于启发式动态分解算法的矩形件优化排样[J].计算机应用，2013（7）：1908-1911.

[3]Cui Yaodong，Lu Yiping.Heuristic Algorithm for a Cutting Stock Problem in the SteelBridge Construction [J].Computers and Operations Research，2009，36（2）：612-622.

[4]许继影.矩形件优化排样的混合启发式方法[J].计算机工程与应用，2012（13）：234-239.

[5]Carlos G，Carlos A，Luis G.A Hybrid Approach Based on Genetic Algorithms to Solve the Problem ofCutting Structural Beams in a Metalwork Company [J].Journal of Heuristics，2013，19（2）：253-273.

[6]吴忻生，吴超成，刘海明.基于改进遗传算法的矩形件排样优化算法[J].制造业自动化，2013（19）：55-58.

[7]董德威，颜云辉，张尧，等.矩形件优化排样的自适应遗传模拟退火算法[J].中国机械工程，2013（18）：2499-2504.

[8]王淑青，雷蕾，曾仕琦，等.基于改进遗传算法的二维图形优化排样方法[J].工业控制计算机，2012（12）：51-53.

[9]刘琼，张超勇，饶运清，等.改进遗传算法解决柔性作业车间调度问题[J].工业工程与管理，2009（2）：59-66.

[10]李明，黄平捷，周泽魁.基于小生境遗传算法的矩形件优化排样[J].湖南大学学报（自然科学版），2009（1）：46-49.

[11]隗平平，刘斌.基于并行遗传算法的矩形件排样优化[J].组合机床与自动化加工技术，2011（3）：78-82.

[12]王竹婷，刘林，程浩，等.改进的最低水平线搜索算法求解矩形排样问题[J].工程设计学报，2009（2）：98-102.