两种基于相空间重构的电力系统短期负荷预测方法分析

张 立，韩 晶，陈 凯

(1.黑龙江工程学院 电气与信息工程学院，黑龙江 哈尔滨 150050；2.哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

两种基于相空间重构的电力系统短期负荷预测方法分析

张 立1，韩 晶1，陈 凯2

(1.黑龙江工程学院 电气与信息工程学院，黑龙江 哈尔滨 150050；2.哈尔滨工程大学 信息与通信工程学院，黑龙江 哈尔滨 150001)

短期负荷预测是电力系统调度运营部门一项重要的基础工作，预测精度的高低直接影响到电网运行的安全性、经济性以及电能质量。采用符合短期负荷特性的混沌理论对短期负荷进行预测，在相空间重构和混沌识别的基础上，建立短期负荷加权一阶局域多步预测模型和最大Lyapunov指数的预测模型，通过对一组实际的短期负荷数据进行预测，仿真结果表明：两种方法都能较准确地预测短期负荷，对于一周内的预测结果，最大Lyapunov指数预测模型的预测精度略高于加权一阶局域多步预测模型的预测精度。

短期负荷预测；混沌；Lyapunov指数；局域预测；相空间重构

短期负荷预测是电网经济运行和安全控制的前提和依据，准确的短期负荷预测已成为实现电力系统管理现代化的重要内容之一[1]。由于对电力负荷特性分析中所呈现的复杂性和非线性，致使传统的预测方法效果不佳。因此，从电力负荷的非线性角度出发，很多研究者提出了各种基于相空间重构的混沌预测模型应用于电力负荷预测领域,这类预测模型的基础是Packard等人提出的相空间重构理论[2]。混沌预测模型主要分为全域预测模型和局域预测模型两大类，因为全域预测模型的计算复杂度较高，而且抗噪声干扰性较差，所以相比较而言，局域模型更适合于短期负荷的预测。文献[3-6]应用各种混沌预测模型来对电力短期负荷进行预测，并取得一定的预测效果。从现有的文献来看，混沌预测模型在短期负荷预测中的研究已经较多，但将加权一阶局域多步预测模型(Add-weighted One-rank Local-region Multi-steps Method，AOLMM)和最大Lyapunov指数预测模型的预测性能进行比较研究的文献却未见报导。在深入研究加权一阶局域多步预测模型与最大Lyapunov指数预测模型的基础上，本文应用这两种模型对短期负荷进行预测，比较这两种预测模型的性能，得到具有实际应用价值的结论。

1 加权一阶局域法多步预测模型(AOLMM)

针对加权一阶局域法[7]计算量较大，而且存在误差累积效应的不足，文献[8]提出加权一阶局域法多步预测模型。

设中心点XM的参考向量集为{XMi}，i=1,2,…,q，经过k步演化后的其相点集为{XMi+k}，一阶局域线性拟合为

(1)

由加权最小二乘法得

(2)

式(2)可看成是关于ak，bk的二元函数，由偏导得

(3)

经化简

(4)

将式(4)表达为矩阵式，得到

(5)

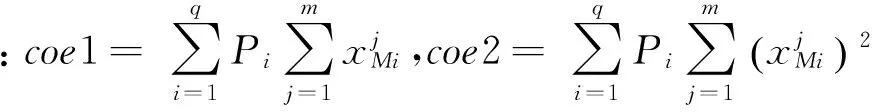
(6)

将求得的ak和bk代入XM+k=ake+bkXM中，即可得到k步演化后的预测值

(7)

2 基于最大Lyapunov指数的预测模型

文献[9]提出了最大Lyapunov指数混沌时间序列预测方法。

(8)

(9)

其中点XM+1只有最后一个元素未知，因此,可以预测式(9)即为最大Lyapunov指数预测模型。

最大Lyapunov指数预测模型的算法为：

1)由混沌系统所得的时间序列计算其嵌入维数m和时间延迟τ，然后重构相空间

(10)

2)计算其最大Lyapunov指数λ1。

3)寻找中心点XM的最邻近点Xk，并计算d=‖XM-Xk‖。

4)计算xM+1，并对根进行取舍。

3 预测实例分析

预测实例所采用的短期负荷数据采自东北某电网，2001年半年每天24h的电力系统小时负荷时间序列进行研究，数据长度N=4380。下面分别用加权一阶局域预测模型和最大Lyapunov指数预测模型对其进行短期预测分析。预测结果的误差标准取为相对误差

(11)

式中:fi表示预测值,xi表示实际值。

首先，根据小数据量法[10]计算得到最大Lyapunov指数为λ1=0.004 8，大于0, 从而验证了该短期负荷时间序列为混沌序列。采用文献[11]所提出的相空间重构联合算法，计算该短期负荷时间序列的重构参数——嵌入延迟和嵌入维数，得τ=4和m=12。由上述求得的嵌入参数进行相空间重构，选取2001-01-01～05-14 134d共3216h负荷时间序列为已知数据。用加权一阶局域多步预测模型和最大Lyapunov指数预测模型进行预测。表1给出了2001-05-15的小时负荷预测结果。由表1可知，加权一阶局域多步预测模型的误差基本小于2%，且误差小于2%的达91.7%，误差大于3%的仅为4.17%；最大Lyapunov指数预测模型误差也基本小于2%，且误差小于2%的为87.5%，大于3%的为8.33%。由表1的预测结果可以看出，针对短期负荷，两种混沌预测方法都能比较准确地预测，对于1d内短期负荷，加权一阶局域多步预测模型的预测精度与最大Lyapunov指数预测模型的预测精度基本相当。

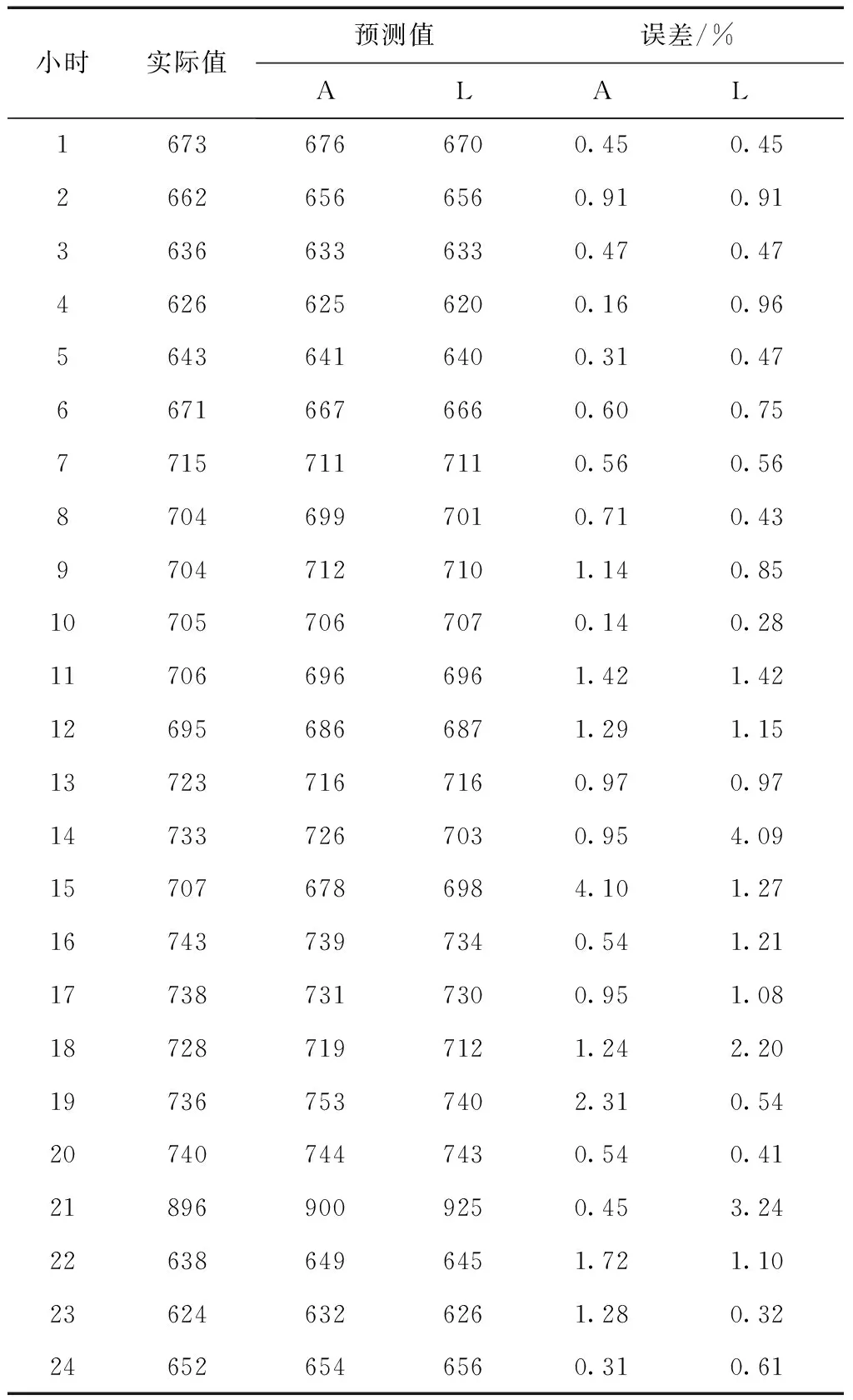
表1 AOLMM模型与最大Lyapunov指数模型的

注：表1中“A”表示AOLMM模型，“L”表示最大Lyapunov指数预测模型。

表2列出了2001-05-15～21一周加权一阶局域多步预测模型和最大Lyapunov指数模型的小时负荷预测误差，加权一阶局域多步预测模型的预测误差平均值小于1%的为66.1%，小于3%的为90.48%，大于3%的仅为9.52%；最大Lyapunov指数预测模型的预测误差平均值小于1%的为65.49%,小于3%的为92.86%,大于3%的仅为7.14%。

注：“A”表示AOLMM模型，“L”表示最大Lyapunov指数预测模型。

由表2的预测结果可以看出，对于一周内短期负荷，基于最大Lyapunov指数预测模型的预测精度略高于加权一阶局域多步预测模型的预测精度。其主要原因在于：基于最大Lyapunov指数预测模型是依据混沌时间序列本身所计算出来的客观规律来进行预测，避免人为主观因素所造成的影响。Lyapunov指数作为对混沌系统初始轨道指数发散的量化指标和用于估计系统混沌水平的一个特征量，是很好的系统预测参数。基于最大Lyapunov指数的短期负荷预测模型充分考虑了信号的内在特性，从而使得其预测结果的可靠性较高。

4 结束语

针对具有非线性特性的电力系统短期负荷时间序列，采用加权一阶局域法多步混沌预测模型和基于最大Lyapunov指数的混沌预测模型，对实际的短期负荷进行了预测。预测结果表明，两种混沌预测模型对短期负荷都具有较好的预测效果，误差符合电力负荷预测的要求。其中最大Lyapunov指数预测模型的预测精度略高于加权一阶局域法多步预测模型的预测精度，更具有实际实用价值。但是基于相空间重构的混沌预测模型，其预测效果依赖于大量的实际数据，致使无法或不便获得大量实测数据的实际系统应用混沌预测方法受到限制，因此，研究小数据量的情况下对实测序列的准确预测有相当的必要性。

[1] 赵宏伟，任震，黄雯莹.基于周期自回归模型的短期负荷预测[J].中国电机工程学报,1997,17(5)：347-351.

[2] Packard N H，Crutchfield J P，Farmer J D，et al.Geometry from a Time Series[J].Physical Review Letters，1980,45(9):712-716.

[3] 穆青青，伍永刚，杨纪明.“负荷趋势+混沌”预测法的改进[J].电力系统及其自动化学报，2013,25(6):160-166.[4] 孙景文，常鲜戎.基于改进混沌理论和ACPSO-LSSVR的短期负荷预测[J].电力科学与工程，2014,30(6):59-65.

[5] 何洋，邹波.基于混沌理论的电力系统短期负荷预测的局域模型[J].华北电力大学学报,2013，40(4):43-50.

[6] ZU Zhe，BI Gui-hong，LIU Li.The Model of Power System Short-Term Load.Conference on Electronic Information and Electrical Engineering[M].Changsha，China，2012:904-911.

[7] 吕金虎，陆君安，陈士华.混沌时间序列分析及其应用[M].武汉:武汉大学出版社，2002.

[8] CAI Minglun，CAI Feng，SHI Aiguo，et al.Chaotic time series prediction based on local-region multi-steps forecasting model[C].Advances in Neural Networks-ISNN 2004：International Symposium on Neural Networks，Part II，Dalian，China，2004.8:418-423.

[9] WOLF A，SWIFT J B，SWINNEY H L，et al.Determining Lyapunov exponents from a time series[C].Physical D:Nonlinear Phenomena,1985,16(3):285-317.

[10] ROSENSTEIN M T，COLLINS J J，DE Luca C J.A practical method for calculating largest Lyapunov exponents from small data sets[J].Physical D，1993，65:117-134.

[11] XIE Zhongyu，WANG Kejun.Selection of embedding parameters in phase space reconstruction.2nd International Conference on Intelligent Computing Technology and Automation[M].Hunan，China，2009.9:637-640.

[责任编辑：郝丽英]

Analysis on power system short-term load forecasting based on two phase space reconstruction methods

ZHANG Li1，HAN Jing1，CHE Kai2

(1.College of Electrical and Information Engineering，Heilongjiang Institute of Technology，Harbin 150050，China；2.School of Information and Communication Engineering，Harbin Engineering University，Harbin 150001，China)

Short-term load forecasting is an important and basic component in the operation of any electric utility of which the accuracy directly influences power system’s security，profit and quality.This paper tries to forecast the short-term load based on the chaotic theory just corresponds to that character.Two chaotic short-term load forecasting melhods based on a local-region multi-steps forecasting model and the largest Lyapunov model are built.Methods are used to predict the real load data.The results show that the two prediction methods can be used in the prediction of load with considerably high accuracy，and the largest Lyapunov model has higher forecasting precision for short-term load in one week.

short-term load forecasting；chaos；Lyapunov exponent；local-region prediction；phase space reconstruction

2014-11-20

黑龙江省教育厅科学技术研究项目(12531540)

张 立(1962-)，女，教授，研究方向：电气工程.

TM715

A

1671-4679(2015)02-0005-03