基于广义等效法的含大规模风电接入的发电系统可靠性评估
张择策,沈天时
(西安交通大学电气工程学院,陕西 西安 710049)
基于广义等效法的含大规模风电接入的发电系统可靠性评估
张择策,沈天时
(西安交通大学电气工程学院,陕西 西安 710049)
只含有传统机组的发电系统,由于可将机组简化为两种状态模型,采用蒙特卡洛模拟法模拟机组状态,其可靠性评估较易实现。由于风的随机性和间歇性,在含有大规模风电接入的发电系统中,不能简单将风电机组看成两种状态模型。因此,提出广义等效法,将风电机组群一步步等效成1个传统机组,并引入zzc系数定义了该等效机组的平均稳定工作时间MTTS。选取RTS79系统作为算例,考虑大规模风电的接入,使用广义等效法计算可靠性指标EENS和LOLE,并与传统蒙特卡洛模拟法的结果进行比较。所提方法为简化风电机组群模型提供了思路,对含大规模风电接入的发电系统可靠性评估有一定指导作用。
风电;可靠性评估;广义等效法;zzc系数;MTTS
0 前 言
发电系统可靠性在电力系统可靠性中至关重要,它直接影响电能的充裕度。风力发电是可再生能源发电形式中技术最成熟、最具开发规模和商业化前景。然而风在时间和空间上鲜明的间歇性和波动性会造成风机出力不稳,这对发电系统可靠性指标的传统计算方式产生了冲击[1-4]。
许多研究者认为,可以将风电机组看成1个多状态机组进行处理,这在一定程度上计入了风电本身的特征。然而,风电机组容量小、数量多,若用传统的模拟法模拟机组状态,在风机数量增多或者风机状态数增多时,将会造成极大的运算量[5-8]。
下面提出了广义等效法,基于概率分布的理论使用按权分配的方法将风电机组群一步步等效成一个传统机组,为实现计算的统一性,引入zzc系数定义了该等效机组的平均稳定工作时间MTTS。为简化风电机组群模型提供了思路,对含大规模风电接入的发电系统可靠性评估有一定指导作用。
1 广义等效法
传统模拟法难以处理大规模多状态风电机组群,其根本原因是将风电机组的地位看成是与传统机组平等的。大量研究者认为,在发电系统可靠性评估中,既然对每个传统机组要单独模拟其状态和状态持续时间,那么对于风电机组也应该做同样的处理[9-11]。这样的思路无疑是忽略了风电机组本身的一些特点。在实际风电机组群中,是大量完全相同的风电机组,它们容量很小,往往整个风电机组群的总容量才相当于1个传统机组。
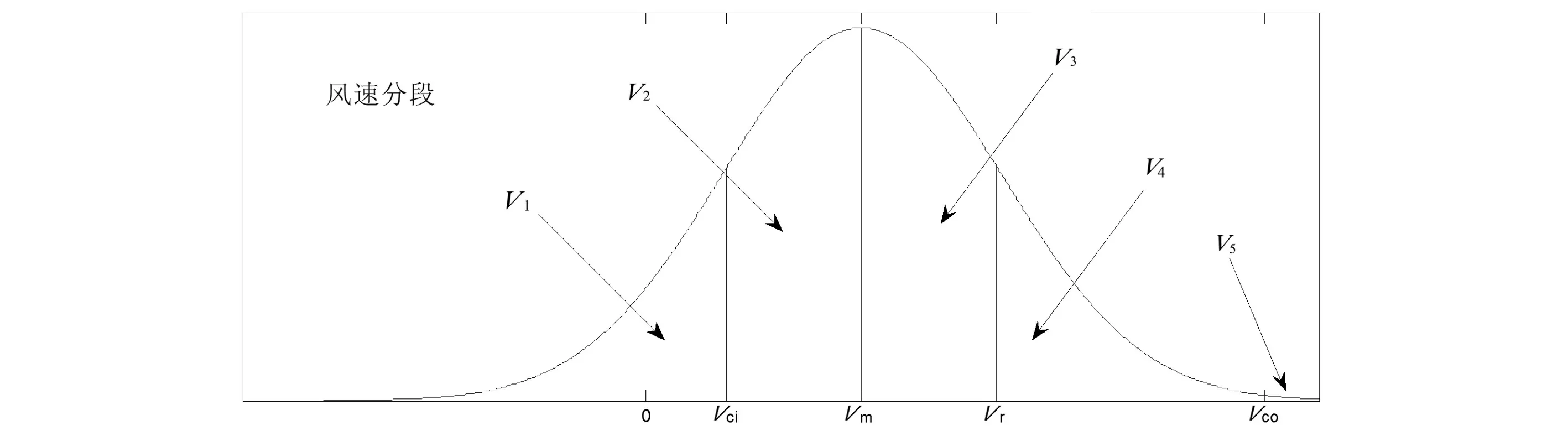
图1 风速分段
因此,提供的思路是将整个风电机组群对发电系统的影响看成是1个等效机组的影响,而在可靠性指标计算中将该等效机组看成传统机组进行处理。广义等效法的实质是在预处理阶段计入风电的间歇性和波动性,而等效后就看成传统机组参与状态模拟,以节省模拟的运算量。
1.1 风电机组群的容量等效
标准正态分布已在工程实践中得到广泛应用,假设当某地的风速统计数据足够长时,则在统计时间内的风速可近似的服从正态分布[8]。
将风速分布划分为如下5个区段[12]:小于切入风速Vci、切入风速Vci和平均风速Vm之间、平均风速Vm和额定风速Vr之间、额定风速Vr和切出风速Vco之间以及大于切出风速Vco,即将所有风速分为落入图中5个区段的5种风速V1、V2、V3、V4、V5,其中,取V2=0.5×(Vci+Vm),V3=0.5×(Vm+Vr)。另外,根据风功率P与风速V的关系,V1、V4、V5对应的P为已知值。
风速分段如图1所示。由于风速服从正态分布,5种风速所对应的概率也容易得到,见表1。
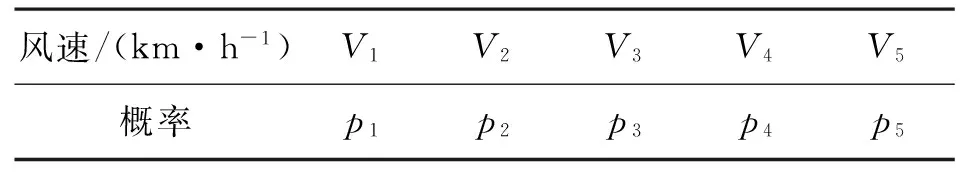
表1 5种风速及其概率
风功率P与风速V的关系如下。
易得各风功率值及其概率,见表2。
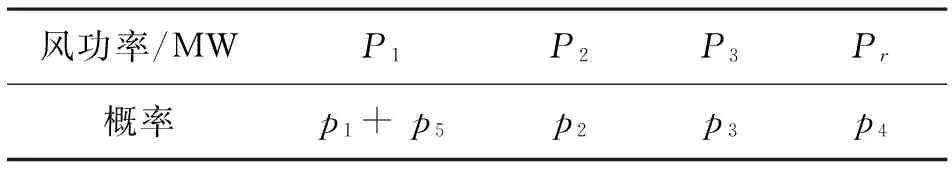
表2 各风功率及其概率
其中P1=0,假设风电机组群由n台额定容量为Pr的风机组成,忽略尾流效应,定义风电机组群的等效容量:
Pw=n(p2×P2+p3+p4×Pr)
至此,将整个风电机组群看成1台容量为Pw的传统机组。
1.2 风电机组群的参数等效
传统机组参与计算的参数有容量P、强迫停运率FOR、平均故障修复时间MTTR和平均无故障工作时间MTTF。上节已得到等效容量Pw,为实现等效,还需要得到风电机组群的广义停运率FORBS、平均故障修复时间MTTR′和1个在公式中用来代替MTTF,表征风电出力稳定性的时间参数——平均稳定工作时间MTTS。
FORBS定义为理论上风机出力为0的频率,即历史风速数据中风速小于Vci以及大于Vco的频率。MTTR′与常规机组一样定义为修复率μ的倒数。
MTTS的定义如下。
首先定义k率,用于表征出现各个不同相邻风速波动的频率。即比较每个相邻小时风速差值的绝对值,设历史数据共有m个小时,则
end
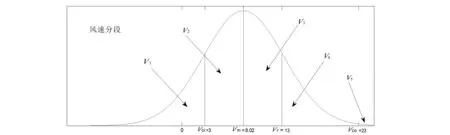
图2 实际风速分段
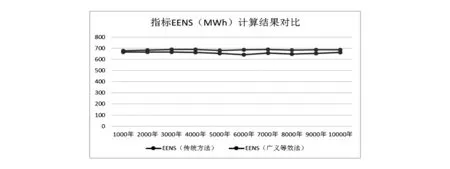
图3 EENS结果对比
不同k率对风机不稳定性的贡献是不同的,因此定义zzc系数与z率,假设相邻k率对z率的贡献相差10倍,公式如下:
z率表征风机综合不稳定性,其中zzc系数用于调整z率的数量级。类比传统机组MTTF的定义,取z率的倒数1/z为平均稳定工作时间MTTS。
2 算例与分析
2.1 算例计算
为验证广义等效法的有效性,下面选用RTS79系统作为算例,该系统含有32台火电机组,总容量3 405MW,年负荷选用RTS79系统负荷数据。已知各单台机组的额定容量、强迫停运率FOR、平均故障修复时间MTTR和平均无故障工作时间MTTF。考虑300台额定功率为1.5MW的风机(修复率已知)接入发电系统,此时的风电渗透率为11.67%。
历史风速数据使用5年(43 648h)的风速数据,其中:
Vm=8.02km/h,σ=5.19km/h,Vci=3km/h,Vco=23km/h,Vr=13km/h
风速分布曲线如图2所示。
按风速服从正态分布计算出5种风速所对应的概率p1~p5见表1。

表3 5种实际风速及其概率
再由风功率P与风速V的关系得到各风功率值及其概率,见表4。

表4 各实际风功率及其概率
计算出等效容量Pw=n×(p2×P2+p3×P3+p4×Pr)=245.314MW,选取风机修复率为0.006 7,计算出平均故障修复时间MTTR′为149.253 7h的风机,广义停运率FORBS为0.095 9,按照1.2的办法求得不同zzc系数下的z率,MTTS如表5所示。
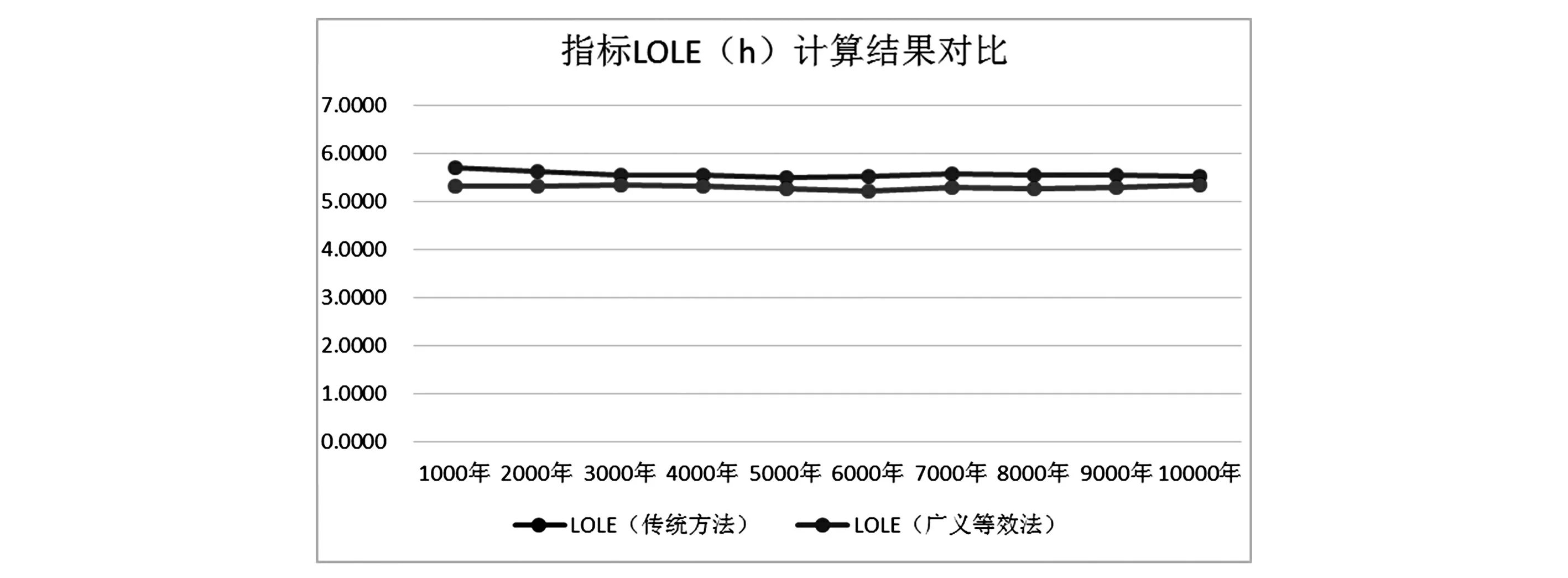
图4 LOLE结果对比
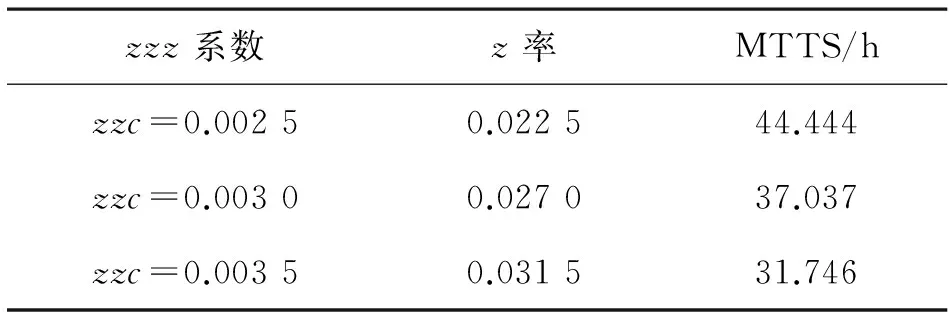
zzz系数z率MTTS/hzzc=0.00250.022544.444zzc=0.00300.027037.037zzc=0.00350.031531.746
至此,将300台组成1.5MW的风电机组群看做RTS系统的第33台传统机组,计算中代入参数Pw、FORBS、MTTR′和MTSS,广义等效完成。
2.2 结果分析
以zzc系数取0.003为例分析,用传统的序贯蒙特卡洛法和广义等效法分别模拟1000年、2000年……10000年的情况,比较指标EENS和LOLE,如图3和图4所示。
从图中可以看出使用广义等效法计算出的指标结果和传统方法的计算结果差别很小,下面再考察指标EENS和LOLE的精度,如图5所示。
当模拟10 000年时,各结果的比较如表6所示。
从表6中数据可以看出,当模拟10 000年时,使用广义等效法与使用传统方法得到的指标差值百分比在5%以下,而指标精度在0.02之上,由此可见广义等效法是有效的。
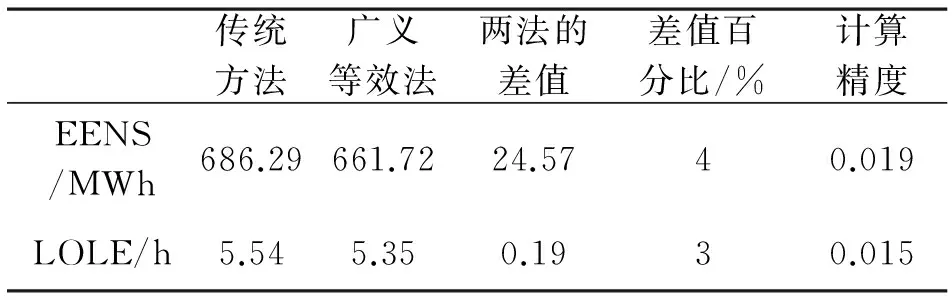
表6 计算结果
3 结 论
1)传统蒙特卡洛模拟法评估含大规模风电接入的发电系统可靠性,其难点在于风机数量增多或风机状态数增多时,运算量很大。小容量风机和传统机组在系统中的地位是不平等的。所提出了广义等效法,将风电机组群一步步等效成1个传统机组。
2)k率表征出现各个不同相邻风速波动的频率,z率表征风机综合不稳定性,不同k率对z率的贡献不同,假设相邻k率对z率的贡献相差10倍,引入zzc系数后定义等效机组的平均稳定工作时间MTTS。
3)选取RTS79系统作为算例,考虑大规模风电(渗透率达11.67%)的接入,使用广义等效法计算可靠性指标EENS和LOLE,当模拟10 000年时(精度均在0.02上),结 果 分 别 为661.72MW和
5.35h,与传统蒙特卡洛模拟法的结果相比误差均在5%以内,有效性显而易见。
4)广义等效不仅是一种方法,更是一种思维。所提方法为简化风电机组群模型提供了思路,对含大规模风电接入的发电系统可靠性评估有一定指导作用。
[1] 余民,杨晏宸,蒋传文,等.风电并网后电力系统可靠性评估和备用优化研究[J].电力系统保护与控制, 2012(12):100-104,135.
[2] 蒋泽甫.风电转换系统可靠性评估及其薄弱环节辨识[D].重庆:重庆大学,2012.
[3] 雷潇.风电机组短期可靠性预测模型与风电场有功功率控制策略研究[D].重庆:重庆大学,2014.
[4] 何禹清, 彭建春,孙芊.考虑风电能量随机性的配电网可靠性快速评估[J]. 中国电机工程学报, 2010(13):16-22.
[5]Dobakhshari,A.S.andM.Fotuhi-Firuzabad.AReliabilityModelofLargeWindFarmsforPowerSystemAdequacyStudies[J].EnergyConversion,IEEETransactionson, 2009,24(3):792-801.
[6]Haghi,H.V.,S.M.Hakimi,andS.M.M.Tafreshi.OptimalSizingofaHybridPowerSystemConsideringWindPowerUncertaintyUsingPSO-embeddedStochasticSimulation[C].inProbabilisticMethodsAppliedtoPowerSystems(PMAPS), 2010IEEE11thInternationalConferenceon. 2010.
[7] 鲍晓慧,侯慧.电力系统可靠性评估述评[J]. 武汉大学学报:上海工学版, 2008(4):96-101.
[8] 蒋小亮.风电并网对电力系统可靠性和备用影响研究[D].上海交通大学,2011.
[9] 曲翀,王晋丽,谢绍宇,等.不同风速模型和可靠性指标对风电可信容量评估的影响[J]. 电网技术, 2013(10):2896-2903.
[10] 石文辉, 别朝红,王锡凡.大型电力系统可靠性评估中的马尔可夫链蒙特卡洛方法[J]. 中国电机工程学报, 2008(4):9-15.
[11] 王学良.风电场可靠性评估研究[D].天津:天津大学,2009.
[12]Karki,R.,H.Po,andR.Billinton.ASimplifiedWindPowerGenerationModelforReliabilityEvaluation[J].EnergyConversion,IEEETransactionson, 2006,21(2):533-540.
[13]Sulaeman,S.,M.Benidris,andJ.Mitra.AMethodtoModeltheOutputPowerofWindFarmsinCompositeSystemReliabilityAssessment[C].inNorthAmericanPowerSymposium(NAPS),2014.
The reliability of power system which only consists of traditional generators is easy to be assessed using Monte Carlo simulation because the generators can be simplified to a two-state model. But the wind turbine generator system cannot be treated as a two-state model in power system considering large-scale wind power integration due to the randomness and intermittent of wind. Hence, generalized equivalent approach is put forward. In this method, wind turbine generator system can be equivalent to a traditional generator step by step and a coefficient namedzzcis introduced to define the equivalent generators′average time of steady operation——MTTS. The RTS79 system is chosen as an example. Considering the large-scale wind power integration, the reliability index like EENS and LOLE are calculated using generalized equivalent approach and its outcomes are compared to those using traditional Monte Carlo simulation. It provides an idea to simplify the model of wind turbine generator system, which has guiding meaning to the reliability assessment of power system considering large-scale wind power integration.
wind power; reliability assessment; generalized equivalent approach; coefficient ofzzc; MTTS
TK89
A
1003-6954(2015)03-0073-05
2015-02-12)

