电力系统低频振荡综合预警方法研究
刘福潮,邢 晶,王维洲,姜希伟,但扬清,刘文颖
(1.国网甘肃省电力公司电力科学研究院,甘肃 兰州 730050;2.国网冀北电力公司电力调度控制中心,北京 100053;3.华北电力大学电力与电子工程学院,北京 102206)
0 引言
随着我国电网互联程度的不断加大,大规模区域电网的形成以及全国联网局面的不断深化,电力系统的稳定运行越来越受到低频振荡的影响,并且互联电网的功率输送能力也受其制约。因此,对电力系统低频振荡的预警技术进行研究,提前掌握可能发生的振荡模式,及时采取手段进行预防控制,对满足电力系统运行经济性的要求,适应不断扩大的电网规模,提高电力系统运行极限意义重大。
传统的阻尼比预警方法仅能区分振荡类型,无法反映强相关机组的参与程度和振幅等信息;而基于小干扰特征值的实用化指标则能对振荡模式进行更加详尽的描述。但是阻尼比的指标和小干扰特征值的实用化指标都与具体的振荡模式对应,不能从整体上对系统发生低频振荡的可能性进行描述。在综合考虑系统运行方式和运行参数对低频振荡影响的基础上,本文根据阻尼比的指标和小干扰特征值的指标提出了一种低频振荡综合预警方法。
1 低频振荡的产生机理
低频振荡的产生机理主要集中在负阻尼机理、强迫振荡机理(共振机理)、非线性机理(分叉和混沌)和强共振机理等方面。其中,负阻尼机理、非线性机理和强共振机理都与电力系统的固有结构和运行参数有关;强迫振荡机理与电力系统的扰动信号有关。
在实际应用中,基于负阻尼机理的Prony分析在工程上被广为接受。由于各个振荡模式之间的相互作用,因此,考虑多种机理的相互配合及各项系统运行的影响因素,建立有效评价系统低频振荡的综合预警指标,对于大电网低频振荡预警的工程实践相当有意义。
2 低频振荡的实用化模型分析
本文采用发电机3阶实用模型,负荷只考虑电压静特性、网络线性,且多机系统只计及转子动态的系统,其线性化状态方程如式(1)所示。
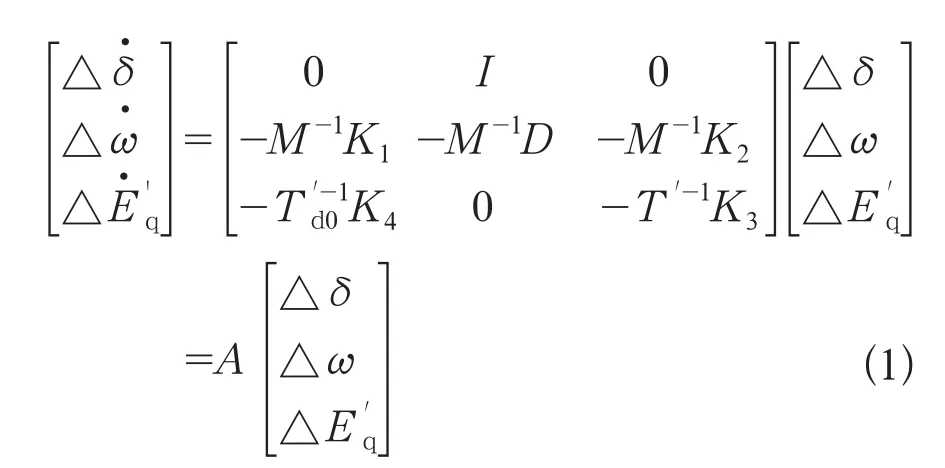
其中,A为系统状态矩阵,M,D分别为转子惯性时间常数及阻尼系数,I为单位矩阵。
由于风电机组定转子之间结构的特殊性,其一般不属于系统的某个振荡模式,即不参与系统振荡;但是随着风电在电网中渗透率的增加,则必须考虑大规模风电集中接入的影响。可在电力系统综合程序(PSASP 6.28)中的实用模型基础上,加入大规模接入的风电参考模型,构建系统小干扰分析的实用化模型,以此作为低频振荡预警系统开发的理论基础。
对于采用异步发电机的风力发电机组,可以采用式(2)所示的异步发电机实用3阶模型。
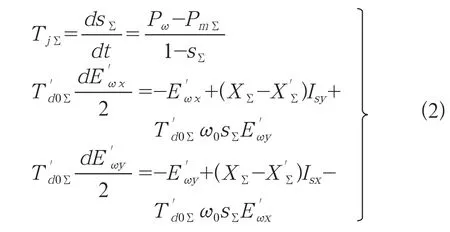
对于双馈型风力发电机组,其建模主要包括双馈型风力发电机组动态建模和换流器建模。在同步旋转的dq坐标系下,根据双馈型风力发电机的电压方程和磁链方程,以及其无功控制部分和有功控制部分方程,则可以得到双馈型风力发电机组小扰动分析的7阶状态矩阵如式(3)所示。
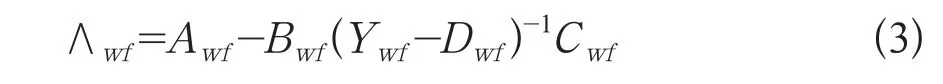
其中,∧wf为系统状态矩阵,其特征值反映系统的小扰动稳定性及低频振荡模式,特征向量反映相应的系统的振荡模式及特性,Awf,Bwf,Cwf和Dwf为包含双馈机组模型的雅可比矩阵,Ywf为风电场对应的节点的矩阵(按实际风电场情况计算)。
其中,
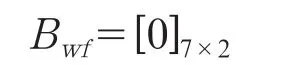
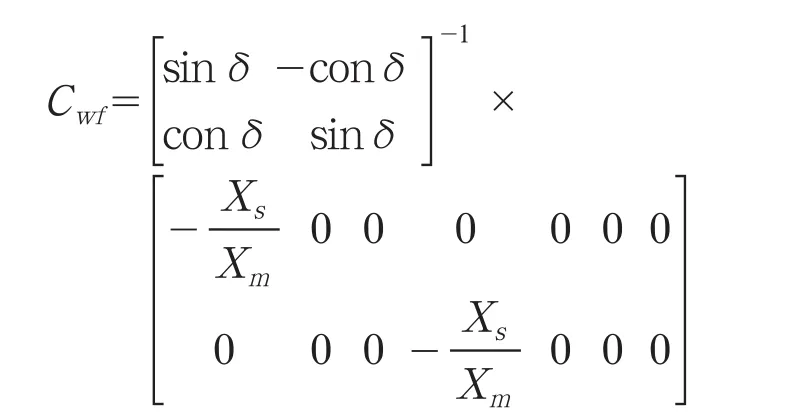

形成双馈型风力发电机组的状态矩阵后,对式(1)所示的全系统线性化状态矩阵进行扩展,即可得到修正后的全系统状态矩阵。
3 综合预警指标的计算及修正
3.1 阻尼比的指标计算
阻尼比的指标既是综合预警指标的组成部分,又为低频振荡预警提供了详细的振荡模式信息。
阻尼比的指标计算主要包括利用逆迭代转Ray leigh(瑞利)商迭代法对系统的状态矩阵进行特征分析,得到状态矩阵的特征值和特征向量,进而计算每一个特征值所对应振荡模式的机电回路相关比和机组相关因子等信息。通过阻尼比的指标对系统的主导振荡模式进行筛选,并根据相关因子确定该振荡模式的强相关机组和重点线路。
由于逆迭代转Ray leigh商迭代法能够求解指定频率范围的特征值,并且不受矩阵阶数的的限制,被广泛应用于工程实际。其流程如图1所示。
对于计算出的全系统n个特征值λi=αi+jΩi,i=1,2,……n。每个特征值所对应自然振荡频率的计算如式(4)所示。



图1 逆迭代转Rayleigh商迭代法流程
阻尼比的计算如式(5)所示。

第k台发电机对第i个振荡模式的相关因子如式(6)所示。

则该振荡模式的机电回路相关比如式(7)所示。
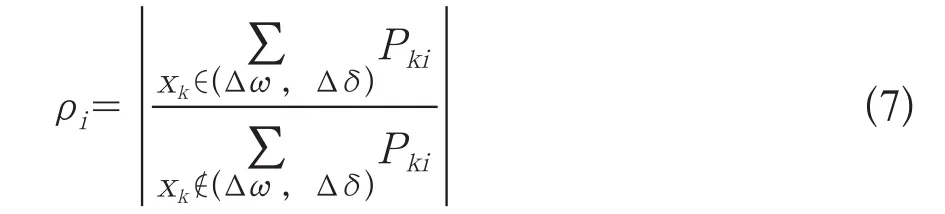
3.2 小干扰特征值的实用化指标计算
由于由振荡模式的特征值计算出的阻尼比只能区分振荡类型,而不能反映强相关机组的参与程度和振荡幅值等信息;下文根据所计算出的主导振荡模式特征值与特征向量,提出了小干扰特征值的实用化指标计算方法,以对振荡模式进行更详细、更具体的描述。
2种振荡模式的模态如图2所示。模态图是将模态的特征向量作为离散点绘制到平面直角坐标系上,其中每一个离散点代表一个发电机组。图2(a)中部分机组与原点附近的其他机组相距较远,是这些机组与主网之间的振荡模式,并且距离原点越远的机组振荡越剧烈。图2(b)中几乎所有机组都在原点附近,没有振荡现象发生。
因此,可以用特征向量中的散点与原点的距离对该振荡模式进行进一步的描述。某一振荡模式αi+jΩi小干扰特征值实用化指标的计算方法如下:
(1) 计算特征向量中每一个散点(xij,yij)与原点的距离lij;
(2) 找出lij≥0.1的点;
(3) 计算符合(2)中的条件的lij的平均值,即为小干扰特征值的指标Ri,若没有符合条件的点,则Ri=0。
3.3 电力系统低频振荡综合预警指标
对低频振荡产生影响的系统运行方式主要包括:电网长链结构和弱联络线,抽水蓄能电站以抽水方式运行,直流输电控制系统、控制模式及交、直流间相互作用。
对低频振荡产生影响的系统运行参数主要包括:短路电流、线路输送功率、主电站备用功率、区域功率以及负荷的波动。
考虑系统运行方式和运行参数对低频振荡的影响,用di,i=1,2,……8,表示电网中是否存在所述情形。若存在所述的某一种情况,则相应的di=-1;否则di=0。例如:若系统中包含长链结构或弱联络线,则d1=-1;否则d1=0。

图2 2种振荡模式的模态图
设综合预警指标为D,则:
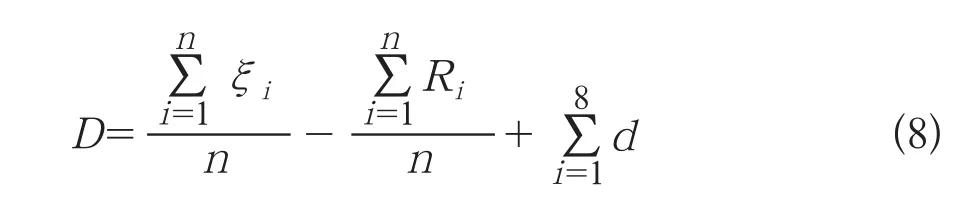
从上述指标可以看出,D越小,系统的网架结构越薄弱,主导振荡模式的阻尼越弱,振荡模式中机组偏离原点的距离越远,发生低频振荡的可能性也越高;D越大,系统的网架结构越坚强,主导振荡模式的阻尼也越大,机组离原点的距离也越近,发生低频振荡的可能性也越低。
3.4 仿真验证
以甘肃电网为研究背景,选取甘肃电网冬天负荷某一运行断面进行小干扰稳定分析计算,所求解的全部特征值对应的特征根分布如图3所示。图中所有特征根均位于虚轴左侧,系统是稳定的。

图3 全部特征根分布
经过筛选和比较,得到该运行方式下的12个主导振荡模式及其强相关机组,如表1所示。
对每个振荡模式的小干扰特征值指标进行计算,其结果如表2所示。

表1 主导振荡模式及其强相关机组

表2 小干扰特征值的指标计算结果
完成阻尼比指标和小干扰特征值指标的计算后,考虑系统的运行状态A:
(1) 山丹-张掖330 kV线路输送功率达到稳定极限;
(2) 主网负荷出现500 MW功率波动。
再对系统运行方式和系统运行参数对低频振荡的影响进行判断,如表3所示。

表3 系统运行方式和参数对低频振荡影响参数的确定
最后根据式(8)计算得到电力系统低频振荡综合预警指标为D=-1.68。利用PSASP暂态计算模块对A运行状态进行仿真计算,山丹-张掖一回330 kV线路1 s三相短路、1.1 s故障切除并且重合不成功时,得到功率振荡曲线。曲线表明A运行状态下,系统失稳,存在低频振荡问题。
适当改变某些发电机组的出力,降低山丹-张掖输送功率至静态稳定极限以下后,按照上述过程重新计算,综合预警指标D=0.07。此时再次应用PSASP软件仿真计算,结果表明山丹-张掖一回330 kV线路1 s三相短路、1.1 s故障切除并且重合不成功时,没有发生振荡现象。
综上所述,在A运行状态下,系统失稳,存在低频振荡问题,其D值为-1.68;在调整后的运行状态下,系统稳定,没有发生振荡现象,其D值为0.07。因此,可以看出综合预警指标D能够反映系统发生低频振荡可能性的大小,具有一定的参考价值。
4 结束语
本文在考虑大规模风电集中接入的基础上建立了电力系统低频振荡分析的全系统实用数学模型,利用逆迭代转Ray leigh商迭代法对系统状态方程进行特征分析,求解特征值和特征向量,并根据计算结果筛选主导振荡模式,进一步查找每个振荡模式的强相关机组和重点线路,并对低频振荡预警的阻尼比指标和特征值指标进行实用化计算,在考虑低频振荡多种影响因素的基础上提出了低频振荡综合预警指标。算例仿真结果表明,综合预警指标能够反映系统发生低频振荡可能性的大小,该综合预警方法可行且有效。
1 倪以信,陈寿孙,张宝霖.动态电力系统的理论和分析[M]. 北京:清华大学出版社,2002.
2 王彦敏.基于WAMS的电力系统低频振荡监测与控制方法研究[D].北京:华北电力大学,2008.
3 郝思鹏.电力系统低频振荡综述[J].南京工程学院学报,2003,13(1):1-8.
4 崔小磊.电力系统低频振荡在线预警系统研究[D].北京:华北电力大学,2005.
5 吴复霞.电力系统低频振荡的分析和控制[D].杭州:浙江大学,2007.
6 王铁强,贺仁睦,王卫国,等.电力系统低频振荡机理的研究[J].中国电机工程学报,2002,12(2):21-25.
7 王铁强.电力系统低频振荡共振机理的研究[D].北京:华北电力大学,2001.
8 王 青,闵 勇,张毅威.电力系统低频振荡的机理研究和主要分析方法[J].电气应用,2006,7(25):1-4.
9 Cansin Y.Evrenosoglu,A li Abur,Ergun Ak leman.Th ree dim ensional visualization and animation of travelling w aves in pow er sy stem s[J].Electric Pow er System s Research,2007,5(7):876-883.
10 李 晶.变速恒频双馈风电机组动态模型及并网控制策略的研究[D].保定:华北电力大学,2004.
11 周志强.双馈感应风电机组电磁暂态建模、控制及实证研究[D].吉林:东北电力大学,2008.
12 蒋尔雄.关于Ray leigh商迭代法的理论基础[J].高等学校计算数学学报,1990,13(1):78-96.
14 李 芳,郭 剑,吴中习,等.基于PC机群的电力系统小干扰稳定分布式并行算法[J].中国电机工程学报,2007,11(31):7-13.
15 X ing Jing,Liu W eny ing,Liu Qian,et al.GDI and openGL-based imp lementation of visualization fo r th e g rid m ain tenan ce p lann ing sup por t system[C].Shanghai:APPEEC,2012.

