强夯处治粉煤灰路基的显式动力非线性数值模拟
赵明华 乔流 张玲 罗宏 刘猛


摘要:基于显式动力非线性有限元分析方法,利用ANSYS/LSDYNA软件对强夯问题进行分析,得出了显式动力非线性数值模拟方法的一般步骤.结合某路基强夯实例建立三维立体模型,对碰撞过程进行数值模拟,得到了强夯加固范围及夯后土体的应力场、位移场.通过与现场实测数据的比对,验证了显式动力非线性有限元数值模拟方法在强夯问题中的适用性.在此基础上,研究和探讨了岳阳地区强夯处治粉煤灰路基中的夯锤参数选取问题,分析比较了夯后土体的沉降,结果表明同能级下重锤低落距有更好的加固效果.
关键词:强夯;数值模拟;大变形;粉煤灰路基;参数分析
中图分类号:TU470.3 文献标识码:A
随着工业化、城镇化的推进,土地资源愈发紧张,大量工程不得不建立在粉煤灰堆积地区.而粉煤灰地基的承载力较低,往往不能满足工程需要,因此必须进行处理,以使其满足承载力、稳定性和抗变形能力的要求.强夯法凭借其施工工艺简单、经济性好、加固效果明显等优点\[1\]在粉煤灰地基处治中应用\[2\]较多.
然而,与广泛的工程应用相比,强夯的理论研究稍显滞后.强夯过程的复杂性决定了其难以用精确的解析方法求解,其加固机理和设计理论方面尚不成熟,现场施工主要依靠经验公式和试验确定\[3\],大大限制了强夯法的发展和应用.针对这一状况,国内外学者采用数值方法,对强夯过程及夯后土体应力场、位移场等进行了较为系统的研究.
钱家欢等\[4\]运用加权余量法导出了弹性振动问题的边界积分方程,并将其应用于边界元分析强夯问题.Chow等\[5\]基于一维波动方程模拟夯锤和土体之间的相互作用,得出应力波的传播特性.孔令伟等\[6\]在考虑夯锤自重的基础上,结合夯锤刚体运动方程和成层弹性地基空间轴对称动力问题的传递矩阵法,导出了强夯的边界接触应力与沉降在变换域中的解析式.然而,上述方法均是基于小变形假定,在工程实际中,夯击区将产生较大破坏,上述方法得出的结果往往不尽如人意.
随着数值计算方法的发展,显式动力非线性有限元理论\[7\]日趋成熟,为强夯这类非线性大变形问题的求解提供了一种新的选择.Thilakasiri等\[8\]率先采用显式动力非线性有限元软件LSDYNA2D对强夯置换软土进行了数值模拟,得到了夯后土体的应力应变关系,但其采用的仍是二维平面模型.国内研究者于德水\[9\]、杨建华\[10\]、张建辉和杨培轩\[11\]分别利用ANSYS/LSDYNA分析了强夯加固湿陷性黄土、碎石土、风成砂的过程,对强夯法的加固机理及其加固范围进行了探索.
可见在常见土类的强夯研究中,显式动力非线性数值方法已经占有一席之地,取得了一定的成果.相较而言,其在粉煤灰地基中的应用目前尚属空白.
鉴于此,本文首先对显式动力非线性有限元数值模拟的一般方法进行探讨,并通过实例验证其在强夯中的适用性,得到夯后土体应力、应变场及夯沉量.在此基础上,结合岳阳某粉煤灰路基强夯工程,对工程中的夯锤参数方案选择问题进行研究.
1显式动力非线性有限元分析方法
1.1显式动力非线性有限元方法简介
在动力学中,显式算法与隐式算法是两个相对的概念.显式算法主要包括central difference method (即中心差分法),是ANSYS/LSDYNA中的主要求解方法,用于分析大变形、瞬态问题、非线性动力问题.
结构系统的通用运动学方程为:
M+C+KU=Rt.(1)
式中:U,Rt,M,C,K分别为结构位移、荷载、质量、阻尼、刚度矩阵.
假定0,t1,t2,…,tn 时刻的节点位移、速度及加速度已知,现求解t+Δt时刻的结构响应.中心差分法对速度、加速度采用中心差分代替,即为:
t=1Δt2(Ut-Δt-2Ut+Ut+Δt),(2)
t=12Δt(Ut+Δt-Ut-Δt).(3)
将式(2)和式(3)代入式(1)中,整理可得:
Ut+Δt=t.(4)
式中:
=1Δt2M+12ΔtC;(5)
t=Rt-(K-2Δt2M)Ut-(1Δt2M-
12ΔtC)Ut-Δt.(6)
式(5)和式(6)分别被称为有效质量矩阵、有效载荷矩阵.中心差分法在求解t+Δt瞬时的位移Ut+Δt时,只需t+Δt时刻以前的状态变量Ut和Ut-Δt,然后计算出有效质量矩阵、有效荷载矩阵,即可求出Ut+Δt,故称此法为显式算法\[12\].
显式算法的优点是它既没有收敛性问题,也无需求解联立方程组,其缺点是时间步长受到数值积分稳定性的限制,不能超过系统的临界时间步长.由于强夯是瞬态非线性过程,从解的精度考虑,时间步长也不能太大,这就在很大程度上弥补了显式算法的缺陷.
1.2强夯模型的建立
1.2.1数值模拟简化
强夯过程复杂,影响因素多.为简化计算,在建立强夯碰撞模型时作如下假设:
1) 路基填土土体均质、各向同性;
2) 与地基土相比,夯锤在冲击过程中被认为是刚体,变形忽略不计;
3) 不考虑夯击过程中产生的热能和声能能量损失;
4) 锤体冲击过程是瞬态大变形问题,孔隙水压力的影响很小,故不考虑孔隙水压力.
受篇幅限制,本文只模拟强夯过程中单点夯击的第一击.
1.2.2材料本构模型
夯锤采用刚体材料即LSDYNA3D中的020RIGID.土体的材料模型是本文的一个难点,目前还没有一个可以很好地反映高能量冲击下土体应力应变特征的本构关系.传统的MohrCoulomb模型应用于大变形问题时,计算结果往往不能收敛.彭建兵等\[13\]用DruckerPrager本构模型(简称DP模型)研究冲击荷载下黄土的动力响应问题,取得了较为理想的结果.本文也采用DP模型作为土体本构模型,并通过与实测数据的比对来验证其在强夯数值模拟中的适用性.
1.2.3建模及网格划分
模型包括锤体和土体两部分,本模型可按轴对称进行简化,夯锤和土体均取1/4建模,采用3D solid164八节点六面体实体单元.
由于强夯是瞬态问题,因此夯击影响到的土体深度和宽度是有限的.通过加入适当的边界条件即可模拟无限大土体的情况.对于土体模型深度和宽度的考虑可以根据经验公式和现场试验确定.
为了既能保证计算结果的准确性又尽量缩小模型规模,离夯击中心点较近处,网格较密,离中心点较远处,网格较疏.
强夯碰撞计算时间取0.2 s.时间步长设定为0.4 s,通过在LSDYNA中定义*TIMESTEP下的参数TSSFAC完成.
为消除沙漏模式的变形积累,在LSDYNA中添加沙漏控制卡*HOURGLASS,选择4号模式.
1.2.4接触面、边界条件的建立及荷载的施加
接触时将发生穿透,故采用侵蚀接触选项,通过在LSDYNA3D中定义关键字*CONTACT_ERODING_SURFACE_TO_SURFACE完成.设置夯锤接触面为Master segment,土体接触面为Slave segment.
土体约束分为两部分.在两个对称面(即xz面和yz面)分别约束y方向和x方向位移,底面约束z方向位移,土体模型外侧两个面设置为无反射边界条件*NON_REFLECTING.
本文不模拟夯锤的自由落体,只需对夯锤施加一个初速度即可.重力加速度通过在LSDYNA中定义*Load中的关键字*GRAVITY_PART完成.
1.3工程实例验证
为验证显式动力非线性有限元数值模拟方法的可行性,对某高速公路填土路堤强夯实例建模分析如下.夯锤为铁锤,土体物理力学指标通过试验获得,具体数据见表1.
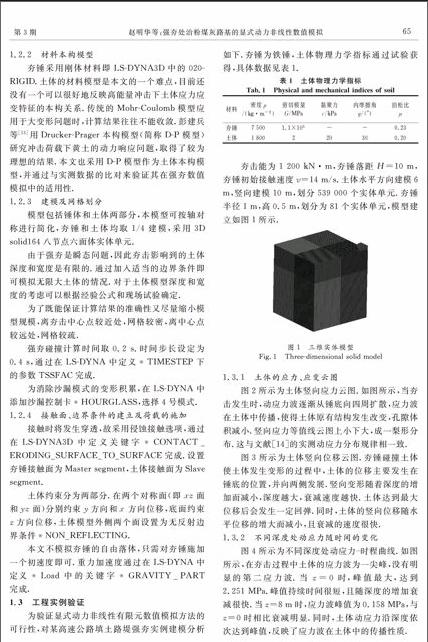
夯击能为1 200 kN·m,夯锤落距H=10 m,夯锤初始接触速度v=14 m/s.土体水平方向建模6 m,竖向建模10 m,划分539 000个实体单元.夯锤半径1 m,高0.5 m,划分为81个实体单元,模型建立如图1所示.
1.3.1土体的应力、应变云图
图2所示为土体竖向应力云图.如图所示,当夯击发生时,动应力波逐渐从锤底向四周扩散,应力波在土体中传播,使得土体原有结构发生改变,孔隙体积减小.竖向应力等值线云图上小下大,成一梨形分布.这与文献\[14\]的实测动应力分布规律相一致.
图3所示为土体竖向位移云图.夯锤碰撞土体使土体发生变形的过程中,土体的位移主要发生在锤底的位置,并向两侧发展.竖向变形随着深度的增加而减小,深度越大,衰减速度越快.土体达到最大位移后会发生一定回弹.同时,土体的竖向位移随水平位移的增大而减小,且衰减的速度很快.
1.3.2不同深度处动应力随时间的变化
图4所示为不同深度处动应力时程曲线.如图所示,在夯击过程中土体的应力波为一尖峰,没有明显的第二应力波.当z=0时,峰值最大,达到2.251 MPa.峰值持续时间很短,且随深度的增加衰减很快.当z=8 m时,应力波峰值为0.158 MPa,与z=0时相比衰减明显.同时,土体动应力沿深度依次达到峰值,反映了应力波在土体中的传播性质.
1.3.3土体竖向位移随深度的变化
图5和图6所示为中心点竖向位移随深度的变化情况.如图所示,随着深度的增加,土体竖向位移减小.当达到最大位移后,土体会发生一定的回弹,稳定后达到最终夯沉量.位于夯锤下方的土体位移最大,回弹也较大,最终夯沉量为0.150 m.当深度达到6 m时,竖向位移仅为3.7 mm.可见,随着深度的增加,土体的竖向位移迅速衰减.由图5可知,土体达到最大位移的时间随深度的增加而推后,这是由于在碰撞中产生了应力波,应力波从夯锤底部向下传播,使得夯锤下土体的位移依次达到最大值.
1.3.4土体竖向位移随水平距离的变化
图7所示为深度0 m, 3 m, 6 m处土体竖向位移随水平距离的变化情况.如图所示,同一深度处,离中心点的水平距离越远,竖向位移越小.同一水平距离处,深度越大,竖向位移越小.当水平距离超过3 m时,可以发现图中3条曲线纵坐标均趋近于0,说明该能级强夯水平影响范围在3 m左右.同时可以观察到,夯击后地表离中心点2 m左右处土体会发生一定的隆起,这与实际情况是一致的.
图8所示为地表夯沉曲线.如图所示,工程实测地表夯沉量为0.131 m\[15\],数值模拟结果为0.150 m,误差为1.9 cm,相对误差14.5%.从整体曲线趋势来看,均反映了随着水平距离的增加沉降衰减以及2 m左右土体发生隆起的现象.
图8所示为地表夯沉曲线.如图所示,工程实测地表夯沉量为0.131 m\[15\],数值模拟结果为0.150 m,误差为1.9 cm,相对误差14.5%.从整体曲线趋势来看,均反映了随着水平距离的增加沉降衰减以及2 m左右土体发生隆起的现象.
2.2强夯处治粉煤灰路基模型的建立
方案1采用轻锤高落距方案.夯锤半径1 m,高0.5 m,落距20 m.夯锤划分为81个实体单元,土体水平方向建模6 m,竖向建模10 m,划分539 000个实体单元.夯锤初始接触速度为v=19.796 m/s.夯击中心处网格加密,边界条件等设定同前,模型如图9所示.
方案2采用重锤低落距方案.夯锤半径1 m,高1 m,落距10 m.夯锤划分为162个实体单元,土体水平方向建模6 m,竖向建模10 m,划分539 000个实体单元.夯锤初始接触速度为v=14 m/s.夯击中心处网格加密,边界条件等设定同前,模型如图10所示.
2.3计算结果比对及分析
就同种土而言,比较强夯加固效果最直观的方法就是比较夯沉量.夯沉量越大,压实度越高,土体工程性质的改善就越为明显.本文将以此为切入点来比较两种方案的加固效果.
2.3.1土体竖向位移随深度的变化
图11和图12所示为中心点不同深度处竖向位移时程曲线.如图所示,z=0时,方案1土体最大竖向位移为0.423 m,到达时间为0.085 s;方案2土体最大竖向位移为0.581 m,到达时间为0.123 s.z=2时,方案1土体最大竖向位移为0.150 m,到达时间为0.091 s;方案2土体最大竖向位移为0.231 m,到达时间为0.138 s.其余深度情况类似,在此不一一赘述.在相同深度处,方案2的最大竖向位移均大于方案1.同时,方案2的曲线更加平缓,到达最大位移的时间较长,这意味着锤体进人土体后相对减速慢,土体所受到的振动持续时间更久,加固时间更长.
图13所示为竖向位移随深度变化情况.如图所示,在相同深度处,重锤低落距方案土体最终沉降要大于轻锤高落距方案土体最终沉降.同时,两条曲线均显示了土体竖向位移随深度增加而衰减的规律.当深度达到8 m时,两种方案的沉降量均已很小,曲线衰减已经很慢.
图13中心点竖向位移随深度的变化曲线
Fig.13The middle settlementdepth curves
2.3.2地表沉降随水平距离的变化
图14所示为地表夯沉曲线.如图所示,轻锤高落距方案地表夯沉量为0.382 m,而重锤低落距方案地表夯沉量为0.552 m,重锤夯沉量比轻锤夯沉量大40%以上.相同能级下,重锤夯击的冲量更大,在锤体进人土体后,相对减速慢,相应的单击夯沉量大,土体压密加固效果好于轻锤高落距,可以产生比轻锤夯击更大的夯坑.同时,轻锤夯击时,周围土体的隆起现象较重锤夯击明显,这在工程中是较为不利的.
3结论
本文对显式动力非线性有限元数值方法的一般步骤进行了探讨,通过实例验证了其在强夯问题中的适用性.在此基础上,探讨了强夯加固粉煤灰中的夯锤参数选取问题,并得出以下结论:
1)数值模拟结果表明,土体竖向变形随着深度和水平位移的增加而减小.锤径2 m且能级为1 200 kN·m时,强夯加固高填土路基的有效影响深度约为6 m,夯点间距不宜超过3 m.
2) 数值模拟结果与工程实测结果基本一致,说明了DP模型可以较好地描述土体在强夯冲击过程中的特性,同时也说明了显式动力非线性有限元方法在强夯问题中的适用性,可以为强夯设计和理论研究提供一定的依据.
3) 通过对强夯处治粉煤灰方案的建模研究发现,在夯击能均为2 400 kN·m且锤径相同的情况下,重锤夯击的单击夯沉量大,加固效果要好于轻锤夯击.同能级下,增大夯锤重量,同时相应减小落距,可以有效减少单点的总夯击次数,提高强夯机具的工作效率,实现缩短工期、降低工程成本的目的.
参考文献
[1]赵明华. 土力学与基础工程\[M\]. 2版. 武汉: 武汉理工大学出版社, 2003: 329-331.
ZHAO Minghua. Soil mechanics and foundation engineering\[M\]. 2nd ed. Wuhan: Wuhan University of Technology Press, 2003: 329-331.(In Chinese)
[2]王起刚. 强夯法在粉煤灰地基中的应用研究\[D\]. 青岛: 中国海洋大学, 2003: 17-26.
WANG Qigang. Study on dynamic consolidation method in coal subground practice\[D\]. Qingdao: Ocean University of China, 2003:17-26. (In Chinese)
[3]龚晓南. 地基处理手册 \[M\]. 2版. 北京: 中国建筑工业出版社, 2000: 277-296.
GONG Xiaonan. Manual of ground treatment\[M\]. 2nd ed. Beijing: China Architecture and Building Press, 2000: 277-296. (In Chinese)
[4]钱家欢, 帅方生. 边界元法在地基强夯加固中的应用\[J\]. 中国科学:A辑, 1987, 29(3): 329-336.
QIAN Jiahuan, SHUAI Fangsheng. Application of BEM to dynamic consolidation\[J\]. Scientia Sinica: Series A, 1987, 29(3): 329-336. (In Chinese)
[5]CHOW Y K, YONG D M, YONG Y, et al. Dynamic compaction analysis\[J\]. Journal of Geotechnical and Geoenvironmental Engineering, ASCE, 1992, 118(8): 1141-1157.
[6]孔令伟, 袁建新. 强夯的边界接触应力与沉降特性研究\[J\]. 岩土工程学报,1998, 20(2): 86-92.
KONG Lingwei, YUAN Jianxin. Study on surface contact stress and settlement properties during dynamic consolidation\[J\]. Chinese Journal of Geotechnical Engineering, 1998, 20(2): 86-92. (In Chinese)
[7]李裕春, 时党勇, 赵远. ANSYS10.0/LSDYNA理论基础与工程实践\[M\]. 北京: 中国水利水电出版社, 2006:11-23.
LI Yuchun, SHI Dangyong, ZHAO Yuan. Basic theory and engineering practice of ANSYS10.0/LSDYNA\[M\]. Beijing: Water Conservancy and Hydropower Press, 2006:11-23. (In Chinese)
[8]THILAKASIRI H S, GUNARATNE M, MULLINS G, et al. Implementation aid for dynamic replacement of organic soils with sand\[J\]. Journal of Geotechnical and Geoenvironmental Engineering, 2001, 127(1): 25-35.
[9]于德水. 强夯法处理湿陷性黄土路基的试验研究及数值模拟\[D\]. 北京: 北京科技大学, 2005: 48-76.
YU Deshui. The experimental study and numerical simulation of the collapse loss ground improved with dynamic consolidation method\[D\]. Beijing: University of Science and Technology Beijing, 2005: 48-76.(In Chinese)
[10]杨建华. 碎石土高路堤的强夯处理与沉降特性研究\[D\]. 武汉: 武汉理工大学, 2008: 75-97.
YANG Jianhua. Settlement property and dynamic compaction improvement parameters study for high crushed stone embankment\[D\]. Wuhan: Wuhan University of Technology, 2008: 75-97.(In Chinese)
[11]张建辉, 杨培轩. 强夯法处理风成砂地基的数值模拟分析\[J\]. 河北大学学报:自然科学版, 2013, 33(2): 127-133.
ZHANG Jianhui, YANG Peixuan. Numerical simulation analysis of treating aeolian sand foundation using dynamic consolidation method\[J\]. Journal of Hebei University: Natural Science, 2013, 33(2): 127-133.(In Chinese)
[12]何文, 钟志华. 显式有限元技术在车身薄壁梁结构件数值模拟中的应用\[J\]. 湖南大学学报:自然科学版, 2005, 32(1): 1-5.
HE Wen, ZHONG ZhiHua. Application of explicit finite element technology to numerical simulation of body thinwalled structure\[J\]. Journal of Hunan University: Natural Sciences, 2005, 32(1):1-5.(In Chinese)
[13]彭建兵, 陈立伟, 邓亚虹, 等. 车辆动荷载作用下黄土暗穴对路基稳定性影响的数值分析\[J\]. 中国公路学报, 2006, 19(4): 17-22.
PENG Jianbing, CHEN Liwei, DENG Yahong, et al. Numerical analysis of subgrade stability influenced by hidden holes in loess under dynamic load of vehicles\[J\]. China Journal of Highway and Transport, 2006, 19(4): 17-22.(In Chinese)
[14]何长明, 邹金锋, 李亮. 强夯动应力的量测及现场试验研究\[J\]. 岩土工程学报, 2007, 29(4): 628-632.
HE Changming, ZOU Jinfeng, LI Liang. Field tests on measurement of dynamic stress of dynamic compaction\[J\]. Chinese Journal of Geotechnical Engineering, 2007, 29(4): 628-632. (In Chinese)
[15]郭乃正, 邹金锋,李亮. 大颗粒红砂岩高填方路基强夯加固理论与试验研究\[J\]. 中南大学学报:自然科学版, 2008, 39(1): 186-189.
GUO Naizheng, ZOU Jinfeng, LI Liang. Dynamic compaction theory and experiments in high roadbed filled with red sandstone\[J\]. Journal of Central South University: Science and Technology, 2008, 39(1):186-189.(In Chinese)

