电子设备热电散热器的节能优化研究

张泠

摘要：{针对环境温度对热电散热器性能影响很大的特点，对采用热电制冷系统冷却的户外电子设备散热器进行了数值模拟研究，并得出了用于设计户外电子设备热电散热器的冷热端最优热导分配比.模拟结果表明：当室外月平均气温为0～40 ℃时，散热器最优热导分配比为0.42～0.54；系统散热器的总热导值从30 W·m/K增至50 W·m/K，单片热电制冷片所承担的冷负荷从20 W增至30 W的情况对散热器的最优热导分配比取值影响很小.

关键词：电子设备；热电制冷；热导分配比；优化

中图分类号：TB657.5 文献标识码：A

在电子设备的发展过程中，散热问题一直是研究重点.特别是光伏逆变器、电信机箱等一些在户外环境下工作的电子设备，它们常常受到太阳热辐射、自身发热等影响，于是户外电子设备散热器的设计成为一个亟待解决的问题.热电制冷已被认为是具有良好应用前景的制冷方式，由于其体积小、结构简单紧凑、无环境污染、容易实现对温度的高精度控制等优点＼[1＼]，得到了广泛的应用与研究，例如热电冰箱＼[2＼]、热电热水器＼[3＼]、热电辐射板＼[4＼]等.

基于热电制冷的诸多优点，国内外的研究人员将热电制冷系统用于电子设备散热，并在电子设备热电散热器的系统分析与控制方面进行了大量研究＼[5-11＼].另一方面，热电制冷系统的性能优化也是研究重点，其中Yilbas和Sahin等＼[12＼]对热电芯片内部的pn结电导壁的体积分配比进行了优化，以提高热电片的制冷性能；Wang和Hung等＼[13＼]针对热电散热器的几何尺寸进行了优化设计，大幅度提升了热电工作效率；Zhao和Tan ＼[14＼]强调了热电散热器冷热端面积分配比、热导分配比对提升热电片效率的重要性并引用了Zhou ＼[6＼]，Zhu ＼[9＼]和Wang＼[15＼]对电子设备热电散热器热导最优分配比的模拟结果.在特定环境下最优热导分配比是0.36～0.47＼[14＼]，Zhang＼[16＼] 和David＼[17＼]分别采用非迭代计算法和控制运行条件对热电制冷系统进行优化设计和管理.但是大部分的研究＼[5-17＼]采用的热电制冷简化模型均将热电内参数设为定值，并且，仅设定系统的热端介质温度恒定在夏季工况的室内热环境.而文献＼[14＼]中提到热电内参数随温度变化的模型在特定场合比简化模型精确10%＼[14＼]，同时，户外电子设备散热量大并且恒定，其散热性能受室外环境影响较大，热电散热器运行时应使热电制冷系统在不同外界气温条件下的制冷量恰好抵消设备散热量.

本文针对全年工作的户外电子设备，对热电系统散热器的热导分配比的节能优化设计进行模拟研究，具有以下特点：1）考虑热电芯片的内参数受冷热端温度的影响；2）高热流密度的户外电子设备热电制冷系统全年工作，热电系统散热器的热端空气介质温度全年变化；3）考虑不同散热器总热导、不同电子设备散热量对模拟优化结果的影响.

1热电制冷系统的模型建立

1.1电子设备热电制冷系统的模型介绍

如图1所示，热电芯片在直流电作用下具有制热制冷的特点.本文数值模拟中选择热电制冷片TEC12706，即芯片具有127对PN结，最大工作电流为6 A.

1.2数学模型

热电制冷片的制冷原理主要是依靠塞贝克效应、珀尔帖效应以及焦耳效应和傅里叶效应来计算单片制冷片的制冷量：

Qc=aITc-K（Th-Tc）-12RI2， （1）

Qh=aITh-K（Th-Tc）+12RI2. （2）

冷端、热端散热器的换热方程分别为：

Qc=KcAc（T′c-Tc），（3）

Qh=KhAh（Th-T′h）.（4）

式中：Qc，Qh分别为热电制冷片的制冷量与制热量；a， k， R， I分别为塞贝克系数、傅里叶系数、电阻、电流；Tc， Th， T′c， T′h分别为制冷片冷热端温度、电子设备表面温度与热端介质空气温度.

图1 热电制冷系统示意图

Fig.1Schematic diagram of TEC system

将系统冷热端散热器的总热导值KA作为一个参数，同时考虑冷热端散热器热导的分配比：

KA=KcAc+KhAh， （5）

x=KcAcKA. （6）

式中：x是冷热端散热器总热导的分配比.

热电制冷片的内参数会随着其冷热端温度变化，根据文献＼[18＼]提供的内参数计算公式，热电系数（塞贝克系数）a可以用温度的4次方的多项式计算：

ac=a1Tc+a2T2c/2+a3T3c/3+a4T4c/4，（7）

ah=a1Th+a2T2h/2+a3T3h/3+a4T4h/4，（8）

a=（ah-ac）/（Th-Tc）. （9）

式中：a1=1.334 5×10-2，a2= -5.375 74×10-5，a3=7.427 31×10-7，a4=1.271 41×10-9.

半导体制冷片的电阻R的表达式采用类似的多项式结构：

rc=r1Tc+r2T2c/2+r3T3c/3+r4T4c/4，（10）

rh=r1Th+r2T2h/2+r3T3h/3+r4T4h/4，（11）

R=（rh-rc）/（Th-Tc）. （12）

式中：r1=2.083 17，r2= -1.987 63×10-2，r3=8.538 32×10-5，r4= - 9.031 43×10-8.

半导体制冷片的热传导率K的表达式如下：

kc=k1Tc+k2T2c/2+k3T3c/3+k4T4c/4，（13）

kh=k1Th+k2T2h/2+k3T3h/3+k4T4h/4，（14）

K=（kh-kc）/（Th-Tc）. （15）

式中：k1=0.476 218，k2= -3.898 21×10-6，k3=8.648 64×10-6，k4= - 2.208 69×10-8.

由于上述各个公式是基于芯片7106型号的数值模拟，对于其他种类型号的制冷片，若其具有电堆数为Nnew，最大工作电流为Inew的制冷片时，则内参数采用如下的转换公式来计算：

anew=a×Nnew71， （16）

Rnew=R×6Inew×Nnew71，（17）

Knew=K×Inew6×Nnew71. （18）

1.3模型结构

本文采用高斯赛德尔迭代数值计算方法，迭代算法的模型结构如图2所示.

图2热电制冷系统模型结构流程图

Fig.2Flow chart of TEC simulation model

2数值模拟试验与结果分析

2.1环境气温对热电制冷系统散热器优化的影响

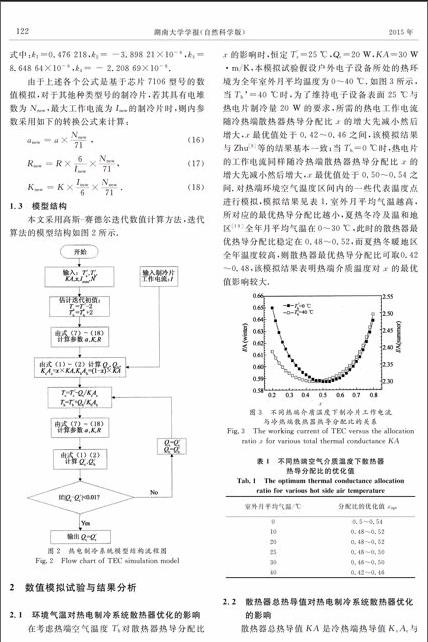
在考虑热端空气温度T′h对散热器热导分配比x的影响时，恒定T′c=25 ℃，Qc=20 W，KA=30 W·m/K，本模拟试验假设户外电子设备所处的热环境为全年室外月平均温度为0～40 ℃.如图3所示，当Th=40 ℃时，为了维持电子设备表面25 ℃与热电片制冷量20 W的要求，所需的热电工作电流随冷热端散热器热导分配比x的增大先减小然后增大，x最优值处于0.42～0.46之间，该模拟结果与Zhu＼[9＼]等的结果基本一致；当T′h=0 ℃时，热电片的工作电流同样随冷热端散热器热导分配比x的增大先减小然后增大，x最优值处于0.50～0.54之间.对热端环境空气温度区间内的一些代表温度点进行模拟，模拟结果见表1.室外月平均气温越高，所对应的最优热导分配比越小，夏热冬冷及温和地区＼[19＼]全年月平均气温在0～30 ℃，此时的散热器最优热导分配比稳定在0.48～0.52，而夏热冬暖地区全年温度较高，则散热器最优热导分配比可取0.42～0.48，该模拟结果表明热端介质温度对x的最优值影响较大.

2.2散热器总热导值对热电制冷系统散热器优化

的影响

散热器总热导值KA是冷热端热导值KcAc与KhAh之和，模拟中的热导值KA与散热器材料特性、接触面积以及散热器与热电片冷热端之间的接触热阻有关.由于目前散热器的发展、热电片与散热器之间连接的加工工艺均较为成熟，对于特定的散热器与热电片的组合，一般认为散热器热导值为定值.参考Zhu 和Tan ＼[9＼]研究热电散热器面积分配比时对散热器冷热端热导值集总化考虑，kc，kh分别取0.12～0.18 W·K-1·cm-2， 0.017 4～0.287 4 W·K-1·cm-2，散热面积取70～110 cm2，对于本文研究则KA取值范围是30～50 W·m/K，分别在夏季、冬季工况下针对不同KA值进行模拟分析.在模拟中设定：T′c=25 ℃，Qc=20 W，T′h=10 ℃和30 ℃分别代表冬季与夏季工况.

图4（a）（b）所示分别为夏季、冬季工况，考虑散热器取不同KA值的情况，制冷片工作电流与冷热端散热器热导分配比的关系曲线图.模拟结果显示：在夏季工况下3种KA值对应的x最优值均处于0.46～0.50，冬季工况下3种KA值对应的x最优值均处于0.48～0.54，说明在一定热端温度下，最优热导分配比不随散热器总热导取值差异而改变，但在同一种工况下，KA值更大的散热器所对应的耗电量更小.

x（a） 夏季工況

x（b）冬季工况

图4不同KA值情况下制冷片工作电流

与冷热端散热器热导分配比的关系

Fig.4Working current of TEC versus the

allocation ratio x for various KA

2.3电子设备散热量对热电制冷系统散热器优化的影响

在Zhou 和 Yu ＼[6＼]的研究中，夏季工况下热电片的制冷量随电流变化在10～46 W之间变化，由于热电片在特定热环境中制冷量的上限主要受到环境温度影响，故在考虑热电片全年工况时，选取单片热电片所承担的冷量在20～30 W之间.在2.1节模拟结果的基础上，针对电子设备散热量分别为Qc=25 W，与Qc=30 W的情况进行模拟，其余参数设定为：T′c=25 ℃，KA=30 W·m/K，T′h=10 ℃和30 ℃分别代表冬季与夏季工况.

图5（a）（b）所示分别为夏季、冬季工况，Qc=25 W与Qc=30 W的情况下，散热器热导分配比与工作电流的关系图.模拟结果显示：夏季工况下，2种情况对应的散热器热导最优分配比均为0.46～0.50；冬季工况下，散热器热导最优分配比均为0.50～0.54，该散热器最优热导分配比的模拟结果与图4（a）（b）中Qc=20 W的情况一致，说明在一定热端温度下，最优热导分配比不随电子设备散热量取值差异而改变.

x（a） 夏季工況

x（b）冬季工况

图5不同电子设备额定散热量Qc情况下

散热器热导分配比与电流的关系

Fig.5Working current of TEC versus the allocation

ratio x for various Qc

3结论

着重考虑全年运行的电子设备热电散热器热端处于动态的热环境中，系统受室外气温影响较大，因此热电片的内参数受冷热端温度的影响不可忽略.引入热电片内参数受冷热端温度影响的数学模型，并在不同热端介质温度、散热器总热导值KA、以及电子设备的额定散热量3个因素影响下，为获得使系统耗电量最小的散热器热导分配比进行了数值模拟试验，研究结果表明：