基于网络DEA 交叉效率的环境效率评价研究

向小东 范秀丽

(福州大学经济与管理学院，福建福州 350116)

一、引言

近年来，随着我国经济的持续快速增长，经济增长与环境保护之间的矛盾日益突出，尽管已经采取了不少相关措施，但环境问题仍日趋严重，不仅直接影响到广大人民群众的身心健康，也严重威胁到国家的可持续发展计划。因此，考虑环境因素的生产效率研究是非常必要的，环境效率逐渐成为衡量环境水平和可持续发展水平的重要指标之一。

已有的相关研究多从企业微观层面、产业层面、国家宏观层面评价环境效率。比如在企业层面，李静引入了一个非径向和非角度的SBM 模型处理非期望产出问题，并对43 家企业进行了环境效率实证分析。［1］在产业层面，钟娜用并联结构的网络DEA 模型对三大产业进行了效率评估。［2］在国家宏观层面，王俊能等利用数据包络分析(DEA)模型对中国大陆31 个省区的环境效率进行了总体分析与评价，并将全国划分为三类环境－经济功能区。［3］李海东等利用改进的环境效率评价模型ISBM－DEA 对中国30 个地区环境效率进行了实证研究。［4］虽然以上文献多数考虑到了环境污染对效率的影响，但是仅仅停留在了非期望产出存在下的效率评价问题，并没有对非期望产出的治理环节作出进一步的评价分析，与实际情况不符。而在相对较少的城市和省际层面的文献中，对环境污染的治理过程同样没有做出评价研究，如辜子寅等以江苏省为研究对象，收集“十一五”期间各地区相关变量数据，运用数据包络分析和Malmquist 指数方法从静态和动态两个角度对区域环境效率进行测度，然后构建面板数据模型，探究环境效率的影响因素，结果表明，政府规制对环境效率改进有正向影响，产业结构和经济外向度的作用具有双面性。［5］赵艳等运用DEA 方法中的SBM 模型对江苏省环境效率及其变化率进行了分析。［6］

由上述四个层面的研究现状可知，目前环境效率评价大多停留在单系统环境效率评价层次上。从整体上把握环境效率评价，具有一定的指导作用，但也存在一定的局限性，表现在忽略了最应考虑在内的非期望产出的治理过程，模糊了环境效率概念。尽管一些文献提及到环境效率评价系统的内部结构，但并没有做出实际的研究。［7］而且，在环境效率评价将系统内部复杂结构考虑在内时，不宜采用单系统DEA 模型而应采用网络DEA 模型。此外，这些已有的环境效率评价研究采用的DEA 方法多数是基于自评思想，最大化自身效率。而实际上，利用自评和互评相结合的交叉效率方法评价环境效率，评价结果会更加客观、可信。基于上述认识，本文从环境污染的产生和治理过程出发将环境效率评价过程划分为生产阶段和污染治理阶段，然后基于网络DEA 和交叉效率评价思想对该两阶段及其构成的系统整体构建环境效率评价模型，最后利用构建的模型对福建省9 个地级市进行应用研究。

二、环境效率评价模型

实际当中，环境问题的产生过程是先经过生产活动，产出经济效益和相应的污染物，然后部分污染物通过环境污染治理，得到污染物综合利用产值和治理后排放的污染物。因此，本文从环境污染的产生和治理过程出发，将环境效率评价分为两个阶段，即生产阶段(子系统1)和污染治理阶段(子系统2)，构建如图1所示的模型图:

图1 两阶段环境效率链形系统模型

考虑如图1所示的两阶段环境效率链形系统模型图，两个子系统分别为生产阶段(子系统1)与污染治理阶段(子系统2)。生产阶段的投入为。其中非期望产出为既是子系统1 的非期望产出向量，又是子系统2 的非期望投入向量。而对于污染治理阶段而言，它的投入是，产出包括非期望产出和期望产出)。这里X1、Y1、Z1、X2、Y2、Y3均是向量。上述向量对应的权重向量分别为v1，u1，u2，v2，u2，u3。对于决策单元j，上述输入、输出向量分别为

根据杨峰的理论，假设:1)每个系统均满足CRS(规模收益不变，对应CCR 模型的一个假设);2)每条链形均可拆分并重新组合，即可以假设虚拟的链形。构造虚拟链形时，原链形具有n 个，构造的虚拟链形也具有n 个，建立次完美链形生产可能集［8］，记作:

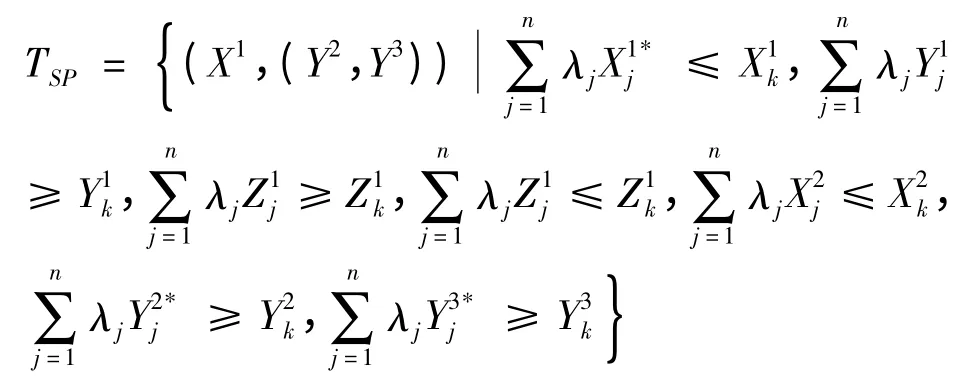
其中:表示生产阶段第j决策单元的前沿投入、表示污染治理阶段第j决策单元的前沿产出。

应用DEA 对环境效率进行评价时面临一个问题:产出中既有期望产出(如GDP 等)，亦存在非期望产出(如“废气”等)，而两者期望的方向并不一致，期望产出越大越好，非期望产出则正好相反，这意味着期望产出与非期望产出必须分别处理。为此，基于 Seiford L.M.，zhu J.的理论［9］对非期望产出的处理方式是对非期望产出乘以－1，然后寻找一个合适的转换向量使所有负的非期望产出变成正值(转换向量法)。如其中v是一个足够大的向量以保证所有转化的期望产出是正数。同样，对于非期望投入人们希望其越多越好，也应该对其做同样的变换处理。具体变换为:其中在以上信息的基础上，构建各子系统和整个网络系统的DEA 交叉效率评价模型。

(一)生产阶段(子系统1)的环境效率评价模型

对于生产阶段(子系统1)效率评估研究，可以分为四个步骤进行。第一步主要是利用CCR模型求得自评效率值;第二步是将第一步求得的带入到中立性交叉效率方法中，获得最优输入输出权重;第三步是利用第二步求得的输入输出权重来求得效率值，从而进一步求得交叉效率矩阵;第四步是利用熵值法和加权求和法得到最终的效率值。具体过程如下。

第一步:根据传统的输入角度的CCR 模型，求 DMUK(表示子系统1 的第k(k=1，2，…，n)个决策单元)自评效率，其线性规划模型如下:

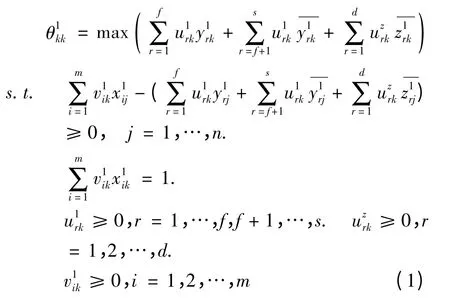
第二步:对每个决策单元，若是直接利用传统DEA 模型中的自评效率值进行排序则存在诸多缺陷，如传统效率值只能分辨出决策单元是DEA 有效还是非有效，不具备对决策单元(尤其是有效单元)进行分级、排序的能力;用于计算效率值的权系数只在对被评价单元最有利(使其效率值最大)的特定范围内取值，容易形成夸大长处、回避缺陷，以自评为主的氛围，产生表面上DEA 有效，但在互评中却处于不利地位的伪有效单元(false positive units)。［10］由于以上问题的存在，学者们开始对传统DEA 模型加以适当的改进和完善，如Sexton 等引入的交叉效率模型。［11］本文提出利用中立性交叉效率评价方法［12］进行环境效率评价以处理由于输入输出权重不唯一问题。相较于其他的DEA 模型，中立性DEA 模型的优势不仅表现在评价单元不会有主观选择斗争性和仁慈性时所面临的困难，而且能有效地减少零输出权重数目，评价指标被尽可能的利用。子系统1 的中立性交叉效率模型如下所示:

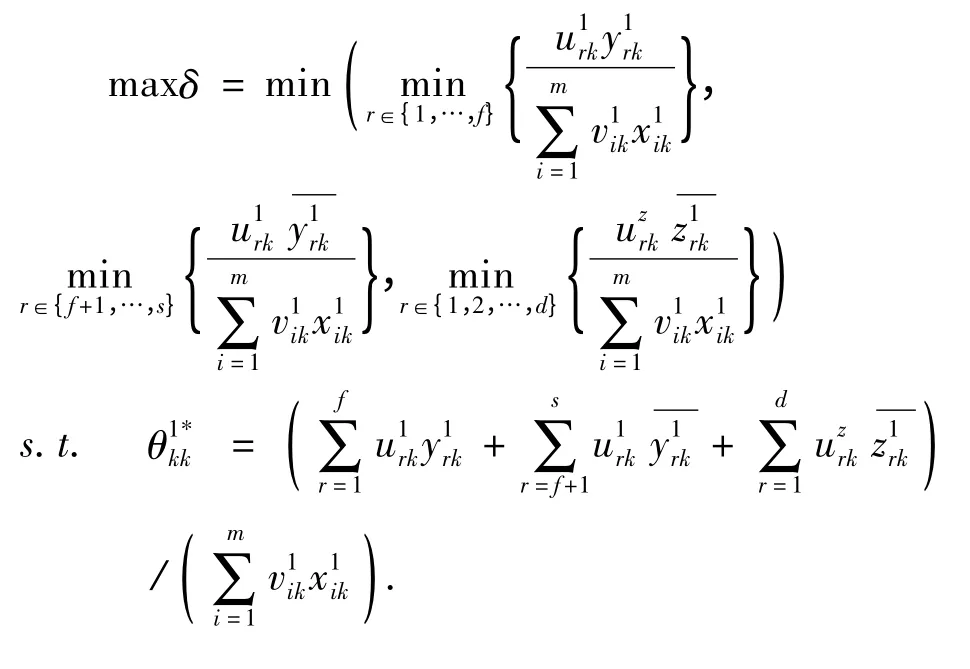
以上目标函数的分式表示是DMUk(k=1，2，…，n)的第r(r=1，2，…，s + d)个输出指标效率值。第一个约束条件表示权重应使得评价单元(子系统1)k满足最大效率为第一步求出来的最优自评效率值;第二个约束条件代表单元j的组合输出不大于组合输入。

模型(2)可转化为如下线性规划:

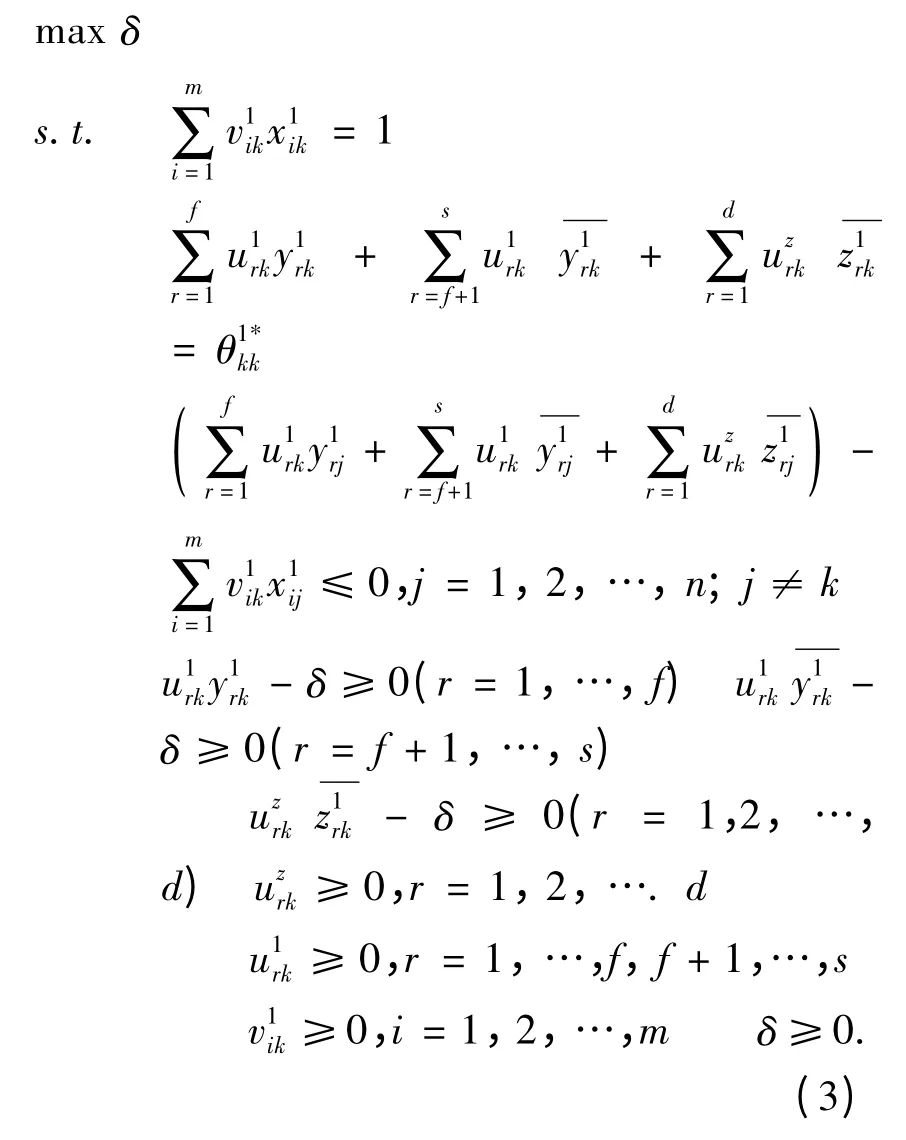
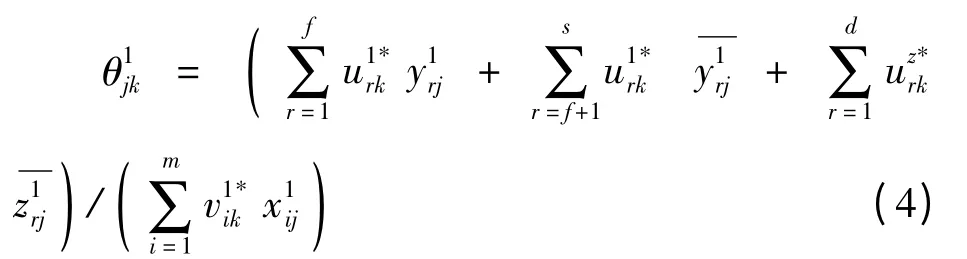
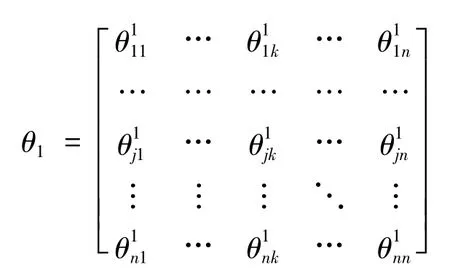
其中主对角线为自评效率值，非主对角线为他评效率值。

第四步:由交叉效率模型计算每个单元的最终效率时常用的处理方法是采用每个决策单元的平均效率，即各单元的权重为1/n。事实上，每个单元所提供的信息量有所不同，为了充分利用各个决策单元所提供的效率评价值的信息，根据Wu Jie 等提出的熵值法［14］来确定权系数wj(j=1，2，…，n)，如下所示:

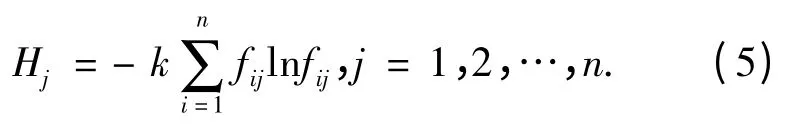
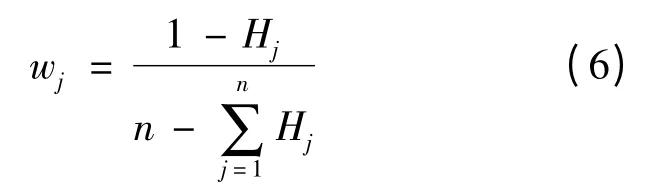
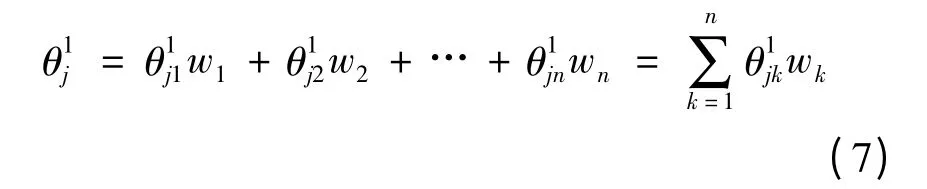
根据以上计算得出的最终效率值，可以对所有决策单元(子系统1)进行排序。

(二)污染治理阶段(子系统2)的环境效率评价

对子系统2，也可以分为四步进行评估研究，类似子系统1 的计算步骤(只是输入输出名称与个数不同，实质思想一样)。

(三)系统整体效率评估

整个网络系统的生产可能集T是由n个虚拟链形系统和n个实际的链形系统共同决定的。按杨峰的理论［15］，本文带两个子系统的系统整体效率评估的具体步骤可分为如下五步。

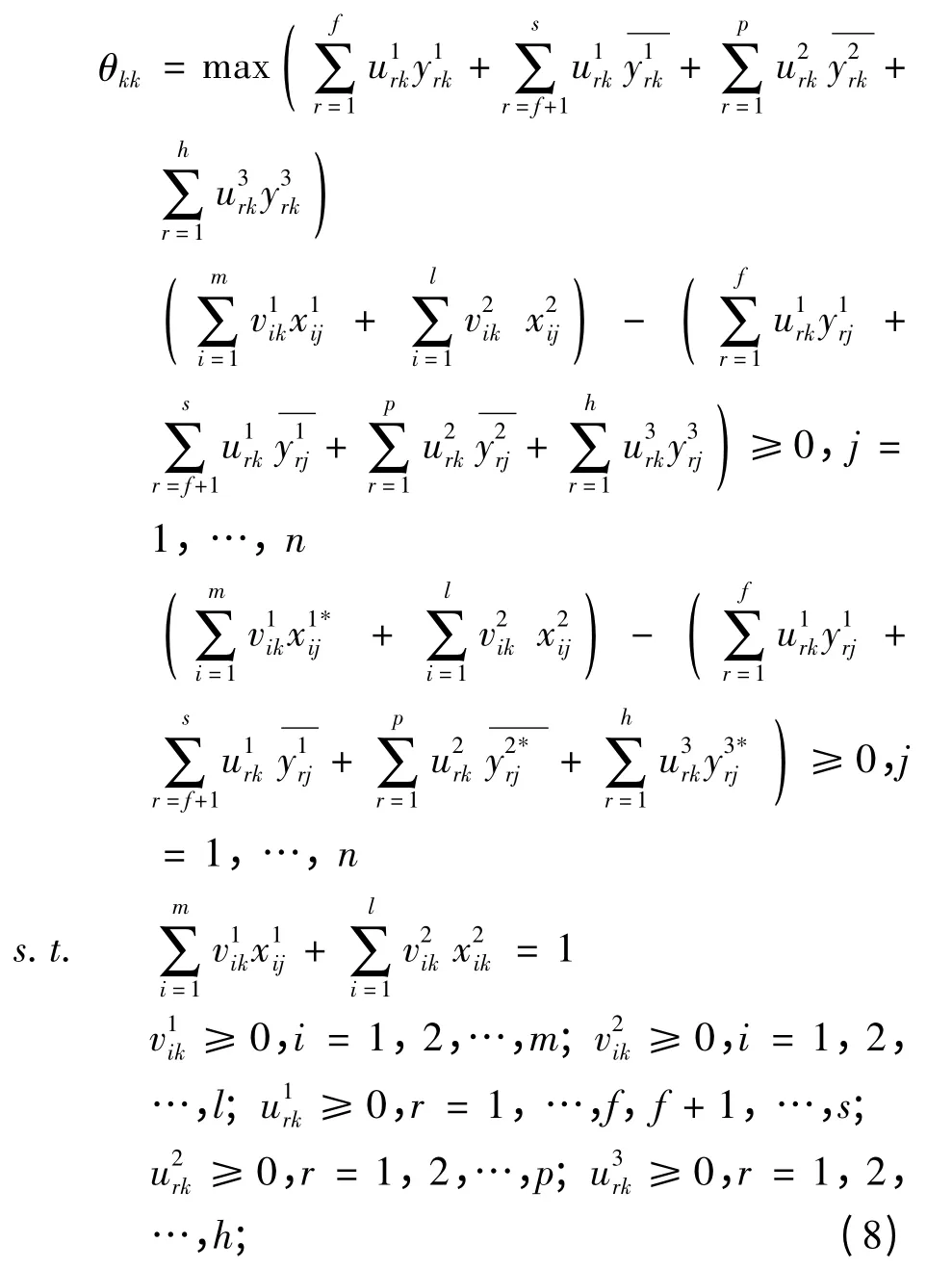
求得的系统整体的目标函数值θkk，即为最优系统整体自评效率值。

第三步:将上述模型(8)得到的整个系统的决策单元的自评效率值应用到中立性交叉效率的线性规划模型中，如模型(9)所示。

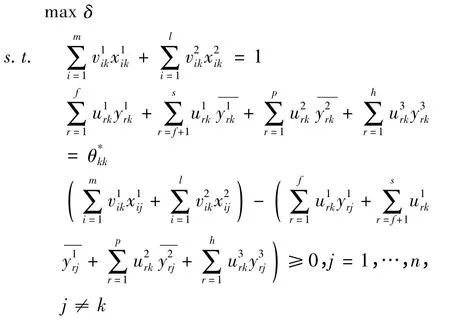
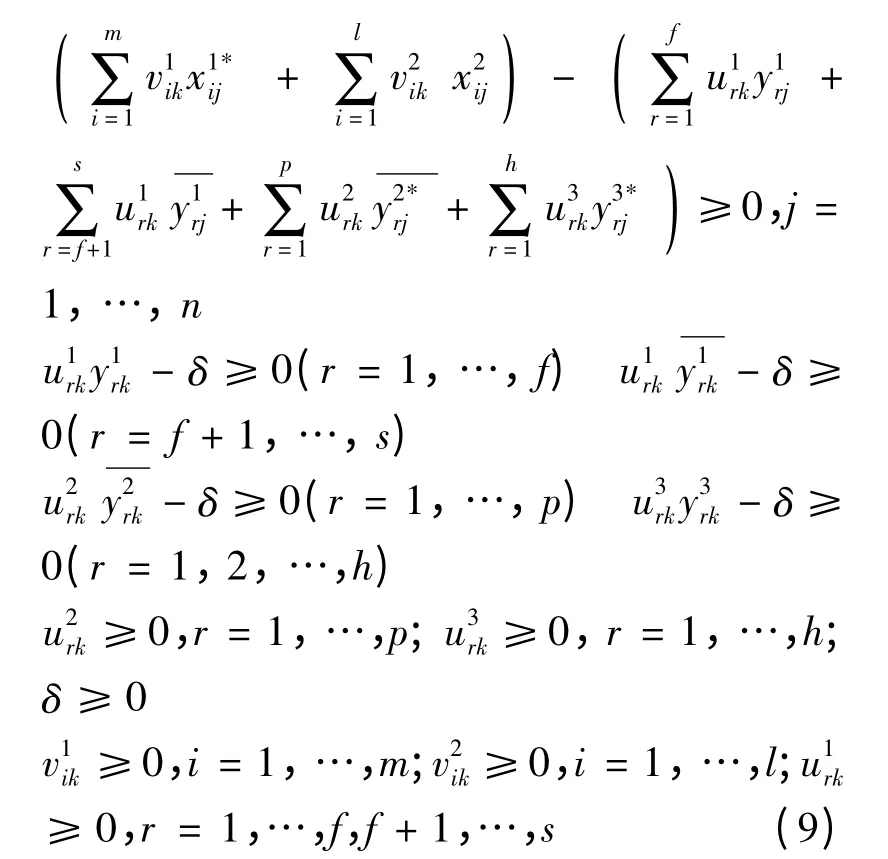
由模型(9)可得到:

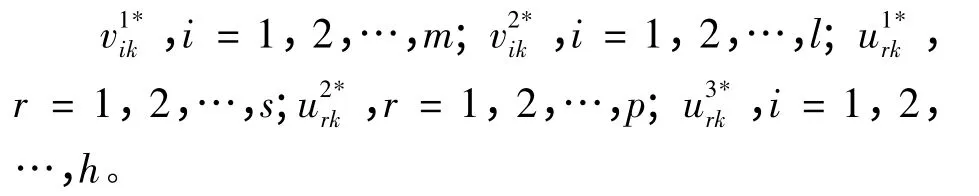
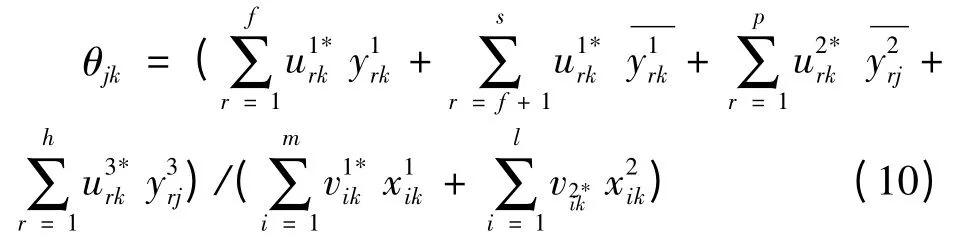
θjk表示决策单元j在决策单元k的最优权重标准下的系统整体效率。每个决策单元进行n次评价从而得到系统整体的交叉效率矩阵θ。

第五步:得到交叉效率矩阵之后，采用熵值法求得决策单元系统整体的权系数，然后确定系统整体的最终效率值。此处类似生产阶段(子系统1)的环境效率评价模型的第四步计算过程。

三、应用

(一)评价指标体系及数据来源

为了说明前述模型的应用，此处以福建省9个地级市为评价对象，把每一个市看成一个决策单元，于是就有9 个决策单元。由于生产活动的投入产出之间存在一定的滞后期［16］，本文将滞后期定为一年，也就是说，第一阶段的输入数据是使用第T年数据，第一阶段的输出数据和第二阶段的输入数据采用第T+1年数据，第二阶段的输出数据选用第T +2年数据。考虑到数据的时效性和可获得性，选用2011－2013年的数据进行分析。根据代表性、科学性和精简性等指标选择原则，参照已有的文献，确定本文的环境效率评价指标体系如下。

生产阶段的投入指标:全社会固定资产投资和单位年末从业人员数(即X1)，这两个指标数据来源于《福建统计年鉴－2012》。该阶段的产出指标:地区生产总值(期望产出)、生活废水排放量、生活二氧化硫排放量(非期望产出，此两项即模型中的Y1')、工业二氧化硫产生量(即模型中的Z1)。具体而言，除工业二氧化硫产生量作为中间变量且数据来源于《中国城市统计年鉴－2013》外，其他指标都是最终产出变量且数据均来源于《福建统计年鉴－2013》。

污染治理阶段的投入指标:工业二氧化硫产生量(即模型中的Z1)和工业污染治理投资额(即模型中X2，包括人力成本、技术投资成本、脱硫处理设备以及所需的吸收剂或其他原料成本等)。后者为第二阶段追加的投入，其数据来源于《福建统计年鉴－2013》。该阶段的产出指标:工业固体排放量、工业二氧化硫排放量(此处两指标即模型中Y2)和工业“三废”综合利用产品产值(即模型中Y3)，除三废综合利用产品产值外，其他产出指标数据均来自于《福建统计年鉴－2014》。其中，三废综合利用产品产值指标数据未知，通过数据分析，可以利用直线趋势预测方法(t为自变量)预测该指标数值。但是各市所参照的期间年份有所差异:福州市是依照2003－2010年的三废综合利用产品产值预测2013年的三废综合利用产品产值，三明市、泉州市和龙岩市亦是如此;厦门市是依照2003－2009年的三废综合利用产品产值预测2013年的三废综合利用产品产值，莆田市、南平市和宁德市亦是如此;而漳州市是依照2000－2009年的三废综合利用产品产值预测2013年的三废综合利用产品产值。经过对各回归方程的F值测算，在显著性水平为5%时检验通过。

另外，应用中的非期望产出指标按照前文所述的数据转化法进行处理:其中v的取值为各指标的最大数值加1 后所得向量。

(二)环境效率评价结果及分析

采用Microsoft office excel 2007 软件对福建9个地级市的两个子系统及系统整体的环境效率进行评价，结果如表1所示:

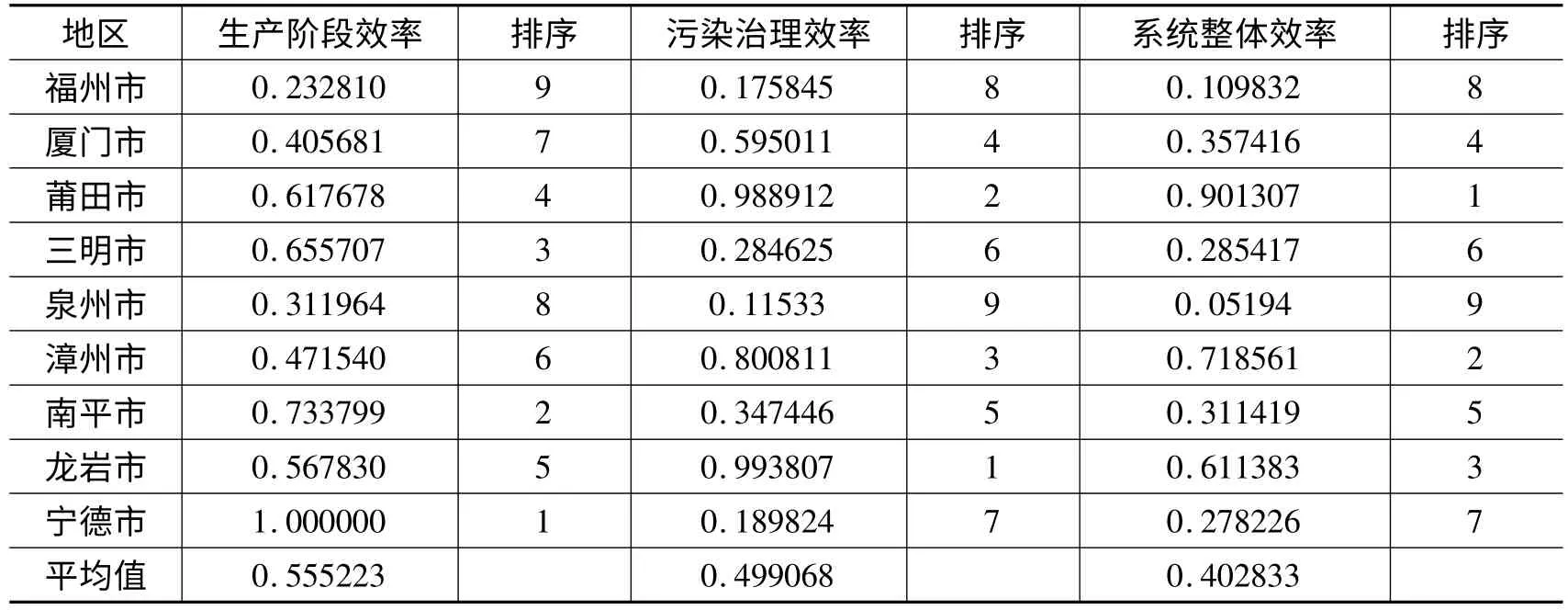
表1 基于2011－2013年数据求得的福建省环境效率评价结果

由表1可知，对于福建省环境效率评价的第一阶段而言，福建省9 个市的生产效率的平均值约为0.56，其中低于平均值的市有4 个，占总数的44.44%，这表明福建省各市在生产阶段的效率还是比较低的，主要是由于生产资源投入冗余或者是生产资源未达到优化配置等所致。具体而言，生产效率高于平均值的五个城市为由大到小排序为宁德市、南平市、三明市、莆田市、龙岩市。宁德市生产效率最高的原因是生产资源达到了最好的优化配置。生产效率排名后三位的市有:厦门市、泉州市、福州市，该三个市是改革开放的前沿城市，经济和城市化水平处于中高阶段，投入指标全社会固定资产投资和单位年末从业人员投入冗余，但是地区生产总值产出不足。以福州市和宁德市作比较，福州市的全社会固定资产投资和单位年末从业人员数分别约是宁德市的6 倍、7 倍，但是福州市的地区生产总值才约是宁德市的4倍，因此表明福州市的地区生产总值产出不足，存在对资源的浪费和利用率不高的问题。

对于福建省环境效率评价的第二阶段而言，福建省9 个市的污染治理效率的平均值约为0.50，其中低于平均值的市有5 个，占福建省市总数的55.56%，这表明福建省各市在污染治理阶段的效率也是比较低的。污染治理效率排名前两位的市:龙岩市、莆田市。一般这类市会根据污染物产生量而投入相应的资金对污染物进行治理。污染治理效率排名后三位的市有:宁德市、福州市、泉州市。一般这类市在对污染物进行治理时因为投入了过多的资源或资金，从而导致污染治理效率偏低。

从整个系统看，福建省环境交叉效率普遍偏低，福建省9 个市的系统整体效率的平均值约为0.40，其中低于平均值的市有6 个，占福建省市总数的66.67%。系统整体交叉效率排名前三位的市有:莆田市、漳州市、龙岩市。一般这类市有几个子阶段的交叉效率相对比较高，或者子阶段之间的协同效应发挥较佳(如莆田市)，因而使得整体的效率也相对比较高。系统整体交叉效率排名后三位的市有宁德市、福州市、泉州市。这类市或者是有几个子阶段的交叉效率相对较高，但由于子阶段之间实现了较差的协同效应(如宁德市)，因而造成系统整体的交叉效率也比较低;或者是各个子阶段的效率都比较低，而影响了系统整体效率的大小。

四、结语

本文构建了环境效率网络DEA 交叉效率评价模型，用此模型对福建省9 个地级市进行了评估研究，结果表明无论是整个系统，还是包含的生产阶段(子系统1)和污染治理阶段(子系统2)，效率值大多数偏低，具有较大提升空间，且各市效率水平差异较为明显，全省发展不平衡。由于文章提出的模型能够有效地分析决策单元内部子系统的有效性水平，能够发掘影响决策单元效率的关键因素，因而能够给出更为详细的环境管理信息，为决策者提供更为有效的决策依据。本文的研究丰富、完善了相关内容，对以后相关应用研究有一定的借鉴意义。

注释:

［1］李 静:《基于SBM 模型的环境效率评价》，《合肥工业大学学报》(自然科学版)2008年第5 期。

［2］钟娜:《基于网络DEA 的产业结构效率评价》，硕士学位论文，中国科学技术大学2011年。

［3］王俊能、许振成、胡习邦等:《基于DEA 理论的中国区域环境效率分析》，《中国环境科学》2010年第4 期。

［4］李海东、汪 斌、熊贝贝等:《基于改进的ISBM－DEA 模型的区域环境效率实证研究》，《系统工程》2012年第7 期。

［5］辜子寅、俞逸帆:《江苏省环境效率的测度及其影响因素实证分析》，《常熟理工学院学报》(自然科学版)2013年第2 期。

［6］赵 艳、孙 翔、朱晓东:《基于DEA 的江苏省环境效率研究》，《环境保护科学》2011年第4 期。

［7］宋马林、王舒鸿、刘庆龄等:《一种改进的环境效率评价ISBM－DEA 模型及其算例》，《系统工程》2010年第10 期。

［8］［15］杨 峰:《含有多个子系统的决策单元的DEA 效率评估研究》，博士学位论文，中国科学技术大学，2006年。

［9］Seiford L.M.，Zhu J.，“Modeling undesirable factors in efficiency evaluation”，European Journal of Operational Research，vol.142，no.1(2002)，pp.16－20.

［10］吴杰:《数据包络分析(DEA)的交叉效率研究－基于博弈理论的效率评估方法》，博士学位论文，中国科学技术大学，2008年。

［11］Sexton T.R.，Silkman R.H.，Hogan A.J.，Data envelopment analysis:critique and extensions.San Francisco :Jossey－Bass，1986，pp.73－105.

［12］Wang Ying－ Ming，Chin Kwai－ Sang，“A neutral DEA model for cross－ efficiency evaluation and its extension ”，Expert Systems with Applications，vol.37.no.5(2010)，pp.3666－ 3675.

［13］荆 浩、赵希男:《DEA 中交叉效率评价的新思考》，《运筹与管理》2008年第3 期。

［14］Wu Jie，Sun Jiasen，Liang Liang，“DEA cross－ efficiency aggregation method based upon Shannon entropy”，International Journal of Production Research，vol，50，no.3(2012)，pp.6726－6736.

［16］Dominique Guellec，Bruno Van Pottelsberghe，“From R ＆ D to Productivity Growth:Do the Institutional Settings and the Source of Funds of R ＆ D Matter”，Oxford Bulletin of Economics and Statistics，vol.66，no.3(2004)，pp.353－ 378.