奇异期权的非参数定价方法研究

冯 玲 贺靖轩 何宇杰

(1.福州大学经济与管理学院，福建福州 350116;2.厦门大学国际学院，福建厦门 361100)

一、引言

2015年 2月 9日，上证 50ETF 期权正式上市交易，意味着我国衍生品市场进入一个崭新的阶段。由于股票交易的卖空限制、交易成本以及资产不完全流动性等因素的存在，现实的金融市场是不完全的，因此基于完全市场假设的传统的期权定价方法不能完全适用，而不完全市场中期权定价的参数难以度量。于是，越来越多的学者从非参数角度研究期权定价。

尽管对期权的非参数定价方法的研究并不少，但绝大多数都是从期权的历史交易价格出发来为新期权定价。由于市场的不完全性，如果期权的历史交易价格不可靠或者很难得到，仅仅依靠期权价格来为新期权定价的非参数方法容易产生定价偏差。Stutzer 提出了正则定价方法，也属于非参数期权定价方法的一种，但它不再严格需要使用期权的交易价格来为新的期权定价，而是直接从标的资产的历史收益数据出发估计新期权的价格。Stuzer 使用该方法对标准普尔500 指数期权进行定价，正则方法估计的期权价格与使用历史波动率的Black－Scholes 定价方法计算的价格很接近。［1］Stutzer 和 Chowdhury 通过对芝加哥期货交易所交易的债券期货期权的实证研究，进一步验证了该方法良好的定价效果。［2］Foster 和Whiteman 就修正的正则定价法展开了讨论。他们分别对债券期货期权和在芝加哥期货交易所交易的大豆期货期权进行了实证分析，结果表明，正则方法均显示了良好的定价效果。［3］［4］

Alcock 和 Carmichamel 将 Stuzer 的经典正则方法与 Longstaff 和 Schwartz 的最小二乘法相结合，提出了加权最小二乘法来为美式期权定价，数值模拟结果显示，该方法无论在常数波动率还是随机波动率情况下，都取得了良好的定价效果和较小的定价偏差。［5］［6］Liu 和 Guo 用正则方法计算出了最优风险中性概率测度，用此概率构造隐含二叉树，应用该树形结构成功地为美式期权定价，在数值实验和实证分析中，该方法都显示了优于Black－ Scholes 模型和经典二叉树方法的定价效果。［7］

Gray、Edwards 和 Kalotay 在利用正则方法对欧式期权定价时，加入了一个交易期权的价格信息，构建了受约束的正则定价方法，通过实证研究表明无约束的正则定价方法并没有比 Black－Scholes 定价模型的表现更好，而加了少数期权价格作为约束条件的正则定价方法，明显减少了平均定价误差。［8］Alcock 和 Auerswald 通过对美式期权的实证研究，证明了加入前一日欧式看涨期权的价格信息能提高定价效果。［9］为了进一步检验受约束正则方法的有效性，Alcock 和Smith 以大量的标准普尔100 指数交易数据为样本，证明了“隐含波动率微笑”和期限结构的存在，当我们使用有期权价格信息约束的正则定价方法时，定价效果超过了使用隐含波动率的Black－Scholes 模型，而且比无约束的正则定价方法显示出更高的定价精度。［10］

综上所述，受约束的非参数正则定价方法，在为期权定价时明显减少了定价偏差，提高了定价精度，但国外学者的研究基本都局限在欧式和美式期权的定价上。本文拟将非参数正则方法拓展到为路径依赖的奇异期权定价，并在计算风险中性概率时，加入约束条件以提高定价精度，最终得到路径依赖型奇异期权的定价公式。

二、奇异期权的受约束正则方法

本文从期权标的资产的历史交易价格出发，计算出历史收益数据，得到真实世界的概率分布。通过最小叉熵原理，将真实概率分布转换为风险中性概率分布，并加入期权价格信息作为约束条件，以提高计算精度。最后，结合路径依赖型奇异期权的具体收益形式，得到期权的定价公式。

(一)标的资产的历史收益

采用离散时间定价方法时，对标的资产价格的观测频率是影响定价精度的一个重要因素。用t 表示当前时刻，T 表示期权到期时刻，将期权期限T－t 分为N 个时间间隔，用tj表示观测时刻，∀j=1，2，…，N。考察M 条股票价格路径，则每一条都由(N+1)个价格元素组成，即当前时刻的价格St和在N个观测时刻的价格

所以，标的资产的价格和收益率相应地由下式表示:

本文假设这M 条股票价格路径在真实世界中是服从均匀分布的。用表示经验分布函数，是真实分布π 的一个逼近。

(二)风险中性概率

正则定价方法的核心是将真实世界的概率测度转换为风险中性概率测度。所求的风险中性概率π*(i)，∀i=1，2，…，M必须满足等价鞅测度的性质:

这里，r 为无风险利率。真实的市场是不完全的，可能存在多个符合条件的风险中性概率测度。因此，找出其中最优的风险中性概率测度是本方法的关键所在。根据最小叉熵原理，最优风险中性概率测度就是在满足已知条件下，最靠近真实概率(i)的概率测度，可以通过求最小Kullback－Leibler 距离来得到:

(三)约束条件

期权价格中隐含了为新期权定价所需要考虑的价格敏感因素，如果期权的价格是可靠且可得的，无疑是对新期权定价最有用的信息。因此，一种包含期权价格信息，又不仅仅依赖期权价格的非参数定价方法成为了学者们的研究方向。Gray和 Newman (2005)，Gray、Edwards 和 Kalotay(2007)、Alcock 和 Auerswald(2008)等学者的研究表明，如果同标的相应期权是被准确定价的，将其价格作为约束条件，加入到新期权的定价中，可以提高定价精度。

本文在为奇异期权定价时，加入相同标的的欧式期权价格和美式期权价格作为约束条件，排除相应的奇异期权价格是为了防止循环计算。以无股息股票为标的资产的美式看涨期权，其价格与相同标的的欧式看涨期权相同。又因为欧式看跌期权和美式看跌期权的价格中，所隐含的市场信息相似，为简化分析，选择其中一种作为约束。

所以，本文在为路径依赖型奇异期权定价时，考虑加入欧式看涨期权价格、美式看跌期权价格，以及同时加入这两种期权作为约束条件。为得到准确定价的同标的约束期权的价格，本文采用Black－Scholes 模型计算欧式看涨期权价格Cobs，采用二叉树方法得到美式看跌期权价格Pobs。

加入约束条件后的最优风险中性概率测度可以通过求解下式得到:

求解公式(5)的拉格朗日函数为:

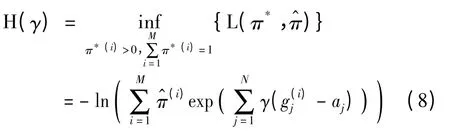
上述最优化问题的解γ*，在无约束条件下是一个M 维的列向量;当加入一个约束期权作为约束条件时，则变为M 行两列的矩阵γ*={γ1，γ2};当同时加入欧式和美式约束期权时，是一个M 行三列的矩阵，γ*={γ1，γ2，γ3}。

(四)奇异期权价格

目前，路径依赖型奇异期权主要有三类:亚式期权、回望期权和障碍期权。本文将通过对几何平均亚式看涨期权(A)、固定回望看跌期权(L)和下跌敲出看涨期权(B)的定价研究，来说明正则方法对路径依赖奇异期权的定价效果。

根据前文推导，通过公式(11)得到了与每条股票价格路径相对应的风险中性概率，将其与奇异期权在相应路径上的贴现收益相乘，即可得到对期权价格的一个估计:

三、数值实验

(一)模拟标的资产价格

正则方法直接从标的资产的历史收益数据出发为期权定价，所以在进行数值实验时，首先需要模拟标的资产的“历史交易价格”，从而得到收益率数据。

在模拟股票价格路径时，假定市场是无摩擦的，标的股票不产生股息和红利，并且利率是常数。将每一个交易日作为时间间隔，每天观测一次标的资产的价格，即dt=1/250年。数值实验的具体参数设定如下:(1)期权的到期期限T=0.1年、0.3年、0.5年 和 1年;(2)时 间 间 隔dt=1/250，因此，观测频率 N=T/dt(取整数);(3)模拟产生 500 条股票价格样本路径，即M=500;(4)无风险利率 r=6%;(5)漂移率μ=10%，波动率σ=20%;(6)当前时刻即在t=0时，股票的价格S0=40 元;(7)障碍期权的障碍水平H=35。

假设股票价格遵循几何布朗运动，则

用Matlab 模拟出500 条股票价格路径，从而得到股票的“历史交易价格”。这里选择其中10条来说明股票价格服从几何布朗运动下的走势情况(见图1)。

图1 标的资产价格路径

得到标的资产在期权期限内的价格后，根据公式(1)得到标的资产的历史收益率R(i)tj。这里任意选取3 条模拟路径，来说明标的资产的价格和收益情况，如表1所示:

表1 标的资产价格及收益率

(二)受约束正则方法求奇异期权估计值

分别以欧式看涨期权、美式看跌期权，以及同时加入欧式看涨和美式看跌期权作为约束条件，来计算风险中性概率，从而求得奇异期权价格的估计值。

以欧式看涨期权作为约束条件时，拉格朗日乘子 γ*={γ1，γ2}，是一个 500* 2 的矩阵，行数等于标的资产的路径条数M，矩阵的列分别与标的资产和约束期权相对应，γ1和γ2是两个相互独立的M 维列向量:

例如，当 T=0.5，X/S0=0.9 时，

根据公式(13)，即可得到为奇异期权定价所需的最优风险中性测度，它是一个M 维的列向量，每一个元素与每一条标的资产价格路径相对应，即赋予每一条价格路径一个风险中性概率:

以美式看跌期权为约束时，计算过程类似上述所示。

同时加入欧式和美式约束期权时，风险中性概率表示为:

其中:

此时，用来得到最优风险中性概率测度π^ * 的拉格朗日乘数 γ*={γ1，γ2，γ3}是一个 M 行 3 列的矩阵，γ1、γ2和 γ3都是 M 维的列向量。

应用Matlab 编程，即可得到各种约束条件和无约束条件下，奇异期权价格的估计值。

四、定价效果分析

蒙特卡罗模拟方法在为路径依赖的奇异期权定价时，相比其他数值方法，具有更大的有效性和更高的弹性。只要模拟次数足够多，能够得到稳定、理想的定价结果。本文将蒙特卡罗模拟方法得到的路径依赖奇异期权的价格作为理论值，来验证受约束正则方法的定价效果。对每个期权进行100000 次模拟，为保证模拟结果的稳定性，每一个期权价格都是重复3 次后得到的平均值。将正则方法计算得到的期权价格作为估计值，蒙特卡罗模拟得到期权价格作为理论值。如果本文的定价方法可行，至少应取得与蒙特卡罗模拟近似的定价结果。

期权到期期限 T 分别为 0.1、0.3、0.5 和 1年，期权价值状态 X/S0 分别等于 0.8、0.9、1 和1.1，考察在不同到期期限和价值状态下，受约束正则方法的定价效果。用A 表示几何平均亚式看涨期权，L 表示固定回望看跌期权，B 表示下跌敲出看涨期权。用 UCAN 表示无约束正则方法，CCANC 表示以欧式看涨期权为约束的正则方法，CCANP 表示以美式看跌期权为约束的正则方法，CCANC ＆ P 表示同时以欧式看涨和美式看跌期权为约束的正则方法。表2显示了正则方法得到的估计值与蒙特卡罗模拟得到的理论值之间的百分比误差。

表2 奇异期权的定价误差(%)

续表2

从总体来看，奇异期权价格的理论值和估计值之间的百分比误差较小，尤其是对价内、平价的亚式期权和回望期权，拟合效果非常好。可见，用正则方法为路径依赖的奇异期权定价是可行的。

进一步分析，对于几何平均亚式看涨期权而言，CCANC ＆ P 的定价误差最小，其次是 CCANC，CCANP 并没有显示比UCAN 更优的定价效果;观察固定回望看跌期权，随着期权价值状态从虚值到平值再到实值的变化，定价误差逐渐减小，进一步说明正则方法对价内期权显示更优的定价效果，且 CCANC ＆ P 对理论值的拟合效果最好，而CCANC 和CCANP 的定价效果差异不大;对障碍期权而言，定价误差略大于前两类奇异期权，CCANC ＆ P 的拟合效果最好。对三类路径依赖奇异期权的定价效果分析可以得到，加入约束条件后，定价误差缩小。可见，在正则方法中加入同标的期权作为约束，可以有效提高定价精度。而加了两种约束期权价格的方法定价效果最好，这也在预料之中。

用正则方法估计奇异期权价格存在某些方面的不足，当期权价外很多，价格很小时，正则方法不够敏感，定价效果不理想。这也可能涉及本文在进行数值实验时的定价精度问题，进一步增加模拟次数M，增加观测频率N，可以在一定程度上提高定价精度。

经过比较分析，用正则方法对路径依赖的奇异期权定价是可行的，取得了与蒙特卡罗模拟近似的定价结果，尤其对实值期权的定价效果最好。而受约束正则方法的定价效果优于无约束正则方法，尤其是加了欧式看涨和美式看跌两类约束期权的正则方法，对理论值的拟合效果最好。可见，在传统正则方法上，加入准确定价的同标的期权价格作为约束，可以有效提高定价精度。

五、结论

本文的研究，为路径依赖型奇异期权的定价提供了一种可行的选择。受约束正则方法是一种非参数期权定价方法，不需要提前作关于波动率、收益分布情况等方面的假设，直接从期权标的资产的历史交易价格中得到定价所需的数据，在市场不完全特征明显的情况下可用于为新期权定价，且该方法定价过程在逻辑上很清晰，容易通过编程实现。

进一步的研究，可以考虑将标的资产的流动性指标、市场限制条件等其它期权价格敏感因素作为约束条件，加入到风险中性概率的计算中，考察其对定价效果的影响;也可以通过在数值实验中进一步放宽假设条件，在更接近现实市场的情况下进行研究。本文在常数波动率和常数利率的环境下进行实验，且采用扩散模型来模拟股票价格路径，证明了该方法为奇异期权定价的可行性。进一步的研究，可尝试使用随机过程来刻画波动率和利率，使用跳－扩散模型来模拟股票价格，以更符合实际市场的动态情况，从而进一步考察该非参数方法的适用性。

注释:

［1］Stutzer，M.，“A simple nonparametric approach to derivative security valuation”，Journal of Finance，vol.51(1996)，pp.1633－1652.

［2］Stutzer，M.，Chowdhury，M.，“A simple nonparametric approach to bond futures option pricing”，Journal of Fixed Income，vol.8(1999)，pp.67－75.

［3］Foster，F.D.，Whiteman，C.H.，“An application of Bayesian option pricing to the soybean market”，American Journal of Agricultural Economics，vol.81(1999)，pp.722－ 728.

［4］Foster，F.D.，Whiteman，C.H.，“Bayesian prediction，entropy，and option pricing”，Australian Journal of Management，vol.31(2006)，pp.181－206.

［5］Alcock，J.，Carmichael，T.，“Nonparametric American option pricing”，Journal of Futures Markets，vol.28(2008)，pp.717－748.

［6］Longstaff，F.，Schwart，E.，“Valuing American options by simulation:A simple least－ squares approach”，Review of Financial Srudes，vol.14(2001)，pp.113－147.

［7］Liu，Q.，Guo，S.，“Canonical distribution，Implied Binominal Tree，and the pricing of American Options”，Journal of Futures Markets，vol.33(2013)，pp.183－198.

［8］Gray，P.，Edwards，S.，Kalotay，E.，“Canonical valuation of options in the presence of stochastic volatility”，Journal of Futures Markets，vol.25(2007)，pp.1－19.

［9］Alcock，J.，Auerswald，D.，“Empirical tests of canonical nonparametrc American option－ pricing methods”，Journal of Futures Markets，vol.30(2010)，pp.509－532.

［10］Alcock，J.，Smith，G.，“Testing alternative measure changes in nonparametric pricing and hedging of European options”，Journal of Futures Markets，vol.34(2013)，pp.320－345.