地下铲运机动态称重系统的理论研究
郭鑫,战凯,顾洪枢,李恒通
(北京矿冶研究总院,北京100160)
地下铲运机动态称重系统的理论研究
郭鑫,战凯,顾洪枢,李恒通
(北京矿冶研究总院,北京100160)
地下铲运机在工作过程中对铲斗物料进行自动称重,当前实际应用中多采用测量举升大臂油缸的油压来计算铲斗中物料的质量。此方案中称重精度的提高是难点,误差产生的原因包括:1)工作机构的摩擦阻尼、地面不平、称重物料重心的变化等客观原因;2)称重模型较为复杂,目前理论分析有不足之处,导致推导的称重计算公式不够精确,只能运用插值、区间测量等手段缩小误差。通过对铲运机称重的力学模型进行分析,设计适合实际应用的称重方案,对此方案推导出更加完善的称重计算公式。找到油压值随举升速度变化的规律,给予合理的理论解释,并做了大量的试验进行验证,形成一套既有理论支撑、同时可应用于工程实际的高精度的地下铲运机动态称重方案。
地下铲运机;动态称重;沿程阻力
地下铲运机是地下金属矿山采矿中的铲装设备,是地下金属矿山的关键装备之一。地下金属矿山的智能化是当前行业的发展趋势,地下铲运机在铲装过程中实现对矿石的自动称重是智能化采矿的一个重要特点。本文将针对地下铲运机的工作特点,设计出一套可应用于实际生产的高精度地下铲运机动态称重系统。
1 力学分析与建模
针对地下铲运机工作机构的工作过程进行力学分析与建模,其铲装工作机构分为Z形反转六连杆机构和正转八连杆机构,由于正转八连杆机构在动臂举升过程中易保持水平,且铲掘力较大,地下铲运机多采用此结构。在建模分析中Z形反转六连杆机构与正转八连杆机构只是推导参数略有差异,故以正转八连杆机构为例进行工作过程的建模,进行力学分析[2]。
地下铲运机铲斗的举升由举升油缸3完成。在力学分析中假设地面水平,物料、举升大臂、油缸和料斗等工作机构处于同一平面,对工作机构进行简化,得出工作过程中机构的受力示意图。
由刚体绕定轴的转动微分方程可知:
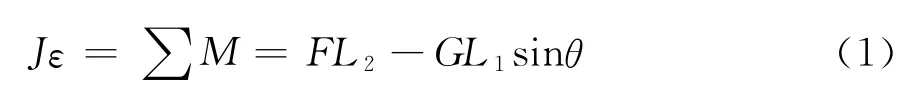
式中:F—举升油缸的伸出力;G—举升大臂及铲斗和物料作为整体的重力;
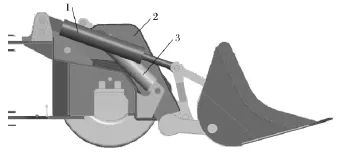
图1 地下铲运机工作机构三维模型Fig.1 The three-dimensional model of working mechanism ofunderground LHD
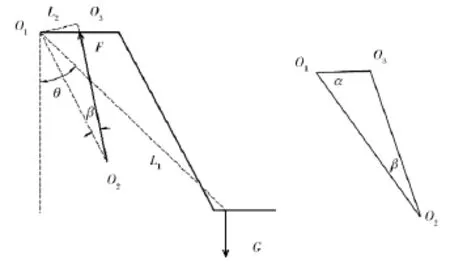
图2 地下铲运机工作机构力学模型Fig.2 The mechanical model of working mechanism ofunderground LHD
O1—举升大臂与机体连接的旋转点;O2—举升油缸与机体连接的旋转点;O3—举升油缸与举升大臂连接的旋转点;α—夹角∠O2O1O3;β—夹角∠O1O2O3;θ—O1与重心G连线与重力方向的夹角;J—举升大臂及铲斗和物料作为整体,绕点O1的转动惯量;ε—举升大臂及铲斗和物料作为整体,绕点O1的角加速度;∑M—举升大臂绕铰接点O1的力矩代数和;L1—举升大臂及铲斗和物料的重心到大臂与机架铰接中心O1的距离;L2—O1到|O2O3|的距离。
由于O3点的角加速度与O1点角加速度相等:

又知L2=|O1O2|×sinβ,在三角形ΔO1O2O3中,根据正弦定理
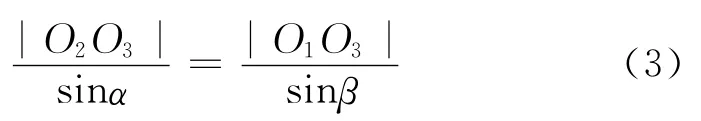
根据余弦定理
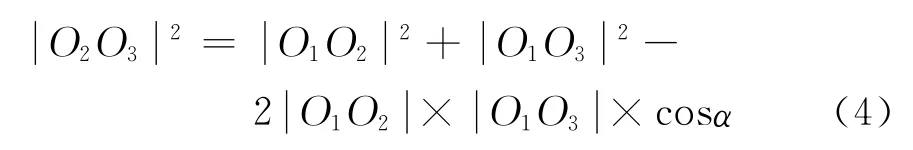
将上述公式代入式(1)中,得
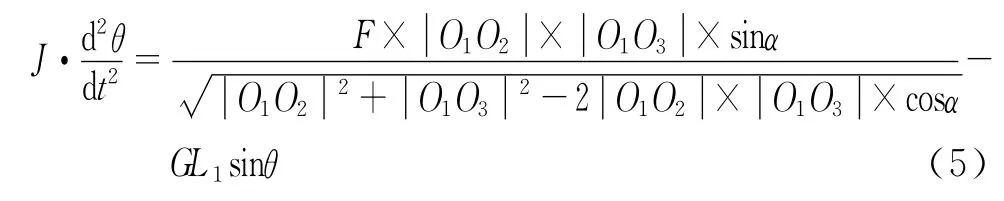
得出G的表达式为
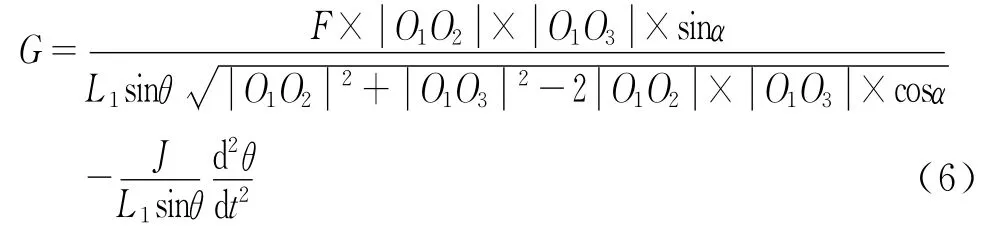
由于α=θ+θ0,其中θ0为角度α与θ一个常量差值。
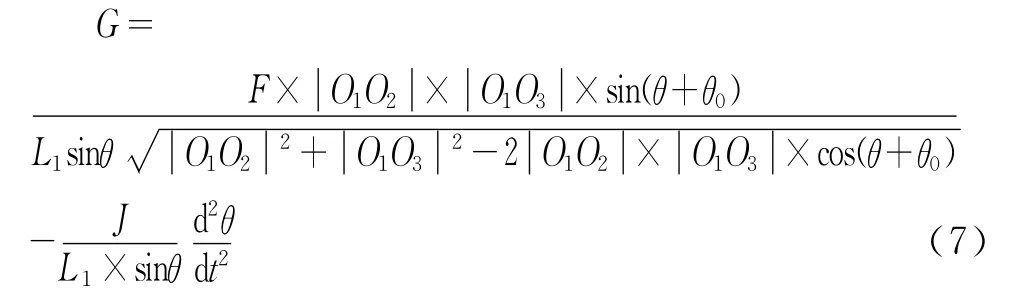
以上公式建模与公式推导过程,有前提条件,即铲运机工作在水平地面。而其实际工作环境是在地下矿山采场,地面条件恶劣。故欲得到符合实际应用的公式,还需要进一步对公式进行修正。
纵向倾斜修正:纵向倾斜对θ角测量有影响,如果采用相对角度传感器,需要在每次称重前对纵向倾斜角度进行一次标定,如果采用绝对水平角度传感器测量计算θ角,则可直接使用测量值。
横向倾斜修正:由于铲运机在横向有10°的自由摆动量,故极限情况横向存在最大20°的倾斜。假定铲运机横向摆动角度为γ,从纵向视角对大臂和矿石的重力进行分析:
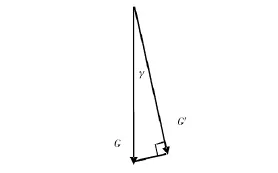
图3 横向倾斜情况下矿石和大臂的重力分析图Fig.3 The gravity analysis diagram of lifting arm and ore under the lateral tilt condition
如图3所示,将重力G向举升油缸的力F的方向做投影得到分力G′,代入式(7)中,求得
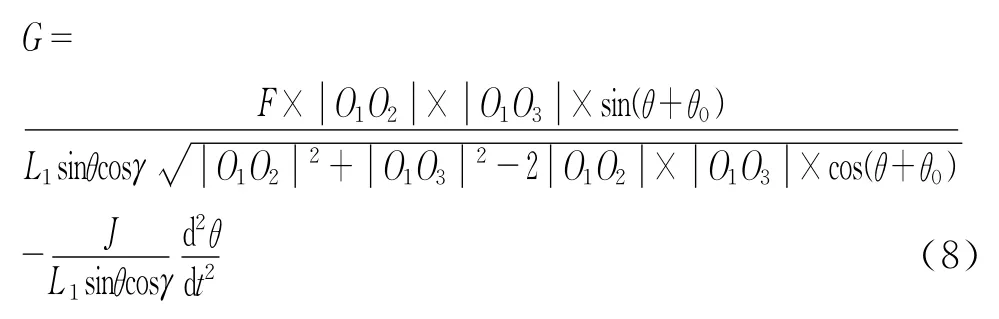
重心偏移修正:在式3中,升大臂及铲斗和物料的重心到大臂与机架铰接中心O1的距离L1,该值并非可测量的常数值,而是随铲斗中物料的位置不同而变化,L1值的精确确定是提高称重精度的一个难题。对于L1值的偏移测量,可在铲运机的转斗油缸上加装液压压强传感器,文献[3]中对此做了公式推导。此处也可借助试验方法解决,即设转斗油缸两端承受压力分别为Fd1、Fd2,通过两端压力值系数修正重心的变化:
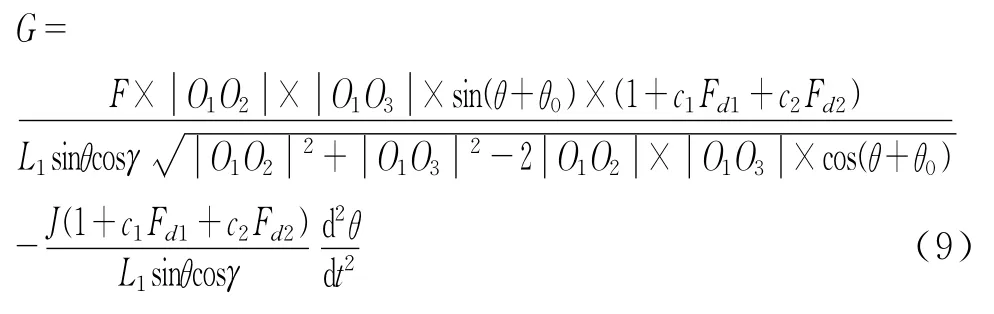
其中c1、c2是表达物料质心偏移的参数,需要通过试验测定。
2 试验方法与理论推导
2.1 传感器的选型
针对公式(9)中出现的变量参数F、θ、γ、Fd1、Fd2,不同的硬件方案,选用的传感器也不同,测量出的参数值并不能直接对应公式中的变量,故式(9)的理论公式需要做进一步的推导,以适用试验中传感器的测量数值。
经过前期大量的试验数据,对式(4)中的各个参数进行分析,将影响因素可以忽略的转斗油缸压力Fd1、Fd2去除,减少传感器数量,在保证精度的前提下使测量方案更精简和快速。故将式(8)定为动态称重方案的基础公式。
选定符合工程应用的传感器,再试验归纳出符合精度的公式,采集数据并将数据代入编写的公式中计算即可。传感器的选取要考虑到设备的使用环境,可靠性高,重复性好,精度高以及安装方便都是选取的原则。
方案选用传感器如下:
1)对于θ、γ值,可选用可测量两维的绝对倾角值的倾角传感器,安装在大臂上,可测量与水平面在纵向的角度χ,χ与θ有常数差值,可设差值为θ1,则;与水平面在横向角度值即为γ值。
2)对于举升油缸的举升力F,则可选用液压压力传感器测量举升油气缸进、出口压力P1、P2来计算F值。
2.2 举升力F的推导计算
在试验中发现油压传感器测量值P1随举升速度的升高而变大,针对这一现象有文献中进行了试验测定,通过区间测量、分段插值等方法来进行增量的补偿[4-5],但产生的原因未做理论研究。经过分析,举升过程中油缸中的油在流动过程中存在压降损失,故对压降损失值做定量分析,可推导出举升力F的计算公式。
如图4举升油缸在大臂举升过程中的受力平衡方程:
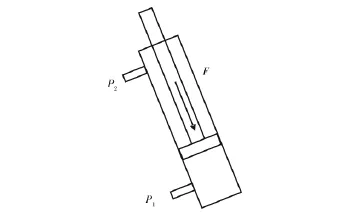
图4 举升油缸受力分析图Fig.4 The stress analysis diagram of lifting cylinder
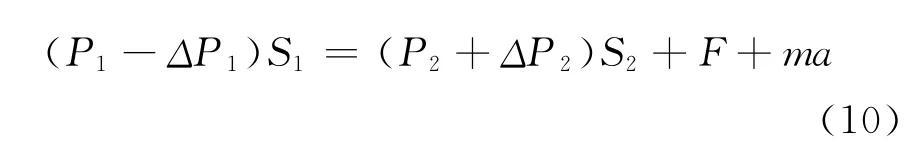
其中m为油缸伸出杆的质量,求出ΔP1、ΔP2值即可得出F值。
ΔP1、ΔP2为油缸进口、出口的压力损失值:
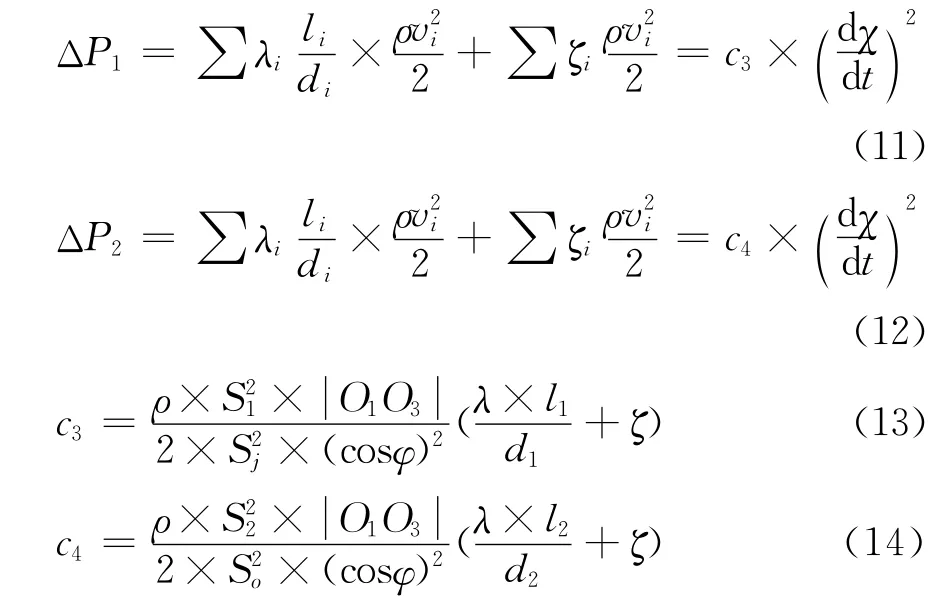
图5对力F进行分解:
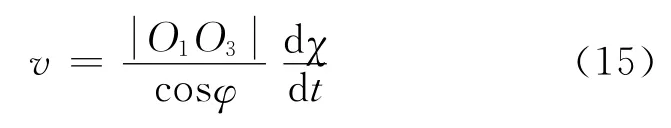
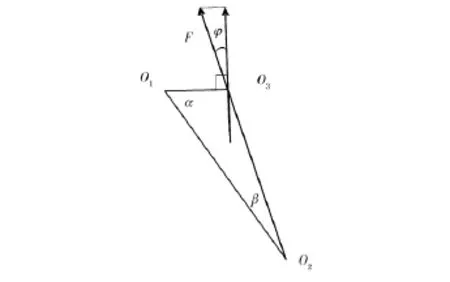
图5 举升油缸线速度分析Fig.5 The analysis diagram of linear velocity of lifting cylinder
上述表达式代入式(10)可得出

将F值代入式(8),并且除以9.8可表示为物料的质量表达式

3 试验验证
对推导出的公式(18)进行试验验证。以2m3地下铲运机为例进行试验,标定1~3.5t的物料,每隔0.5t做一次举升的标定试验,每次标定试验中,针对发动机的转速1 500~2 500r/min,每隔100r/m进行一次举升,记录各个传感器的数据曲线。在记录的数据曲线中,选取χ为50°时的各标定质量、各转速下的采样数据,将代入公式(18)中,解出相关参数值,此试验用的2m3地下铲运机的动态称重公式,即当χ为50°时
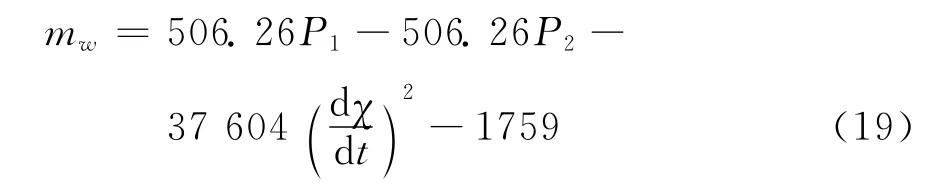
用标定物重新做试验,记录称重控制器计算出的结果,如表1所示,误差小于1%,故推导公式的精确性值得验证。
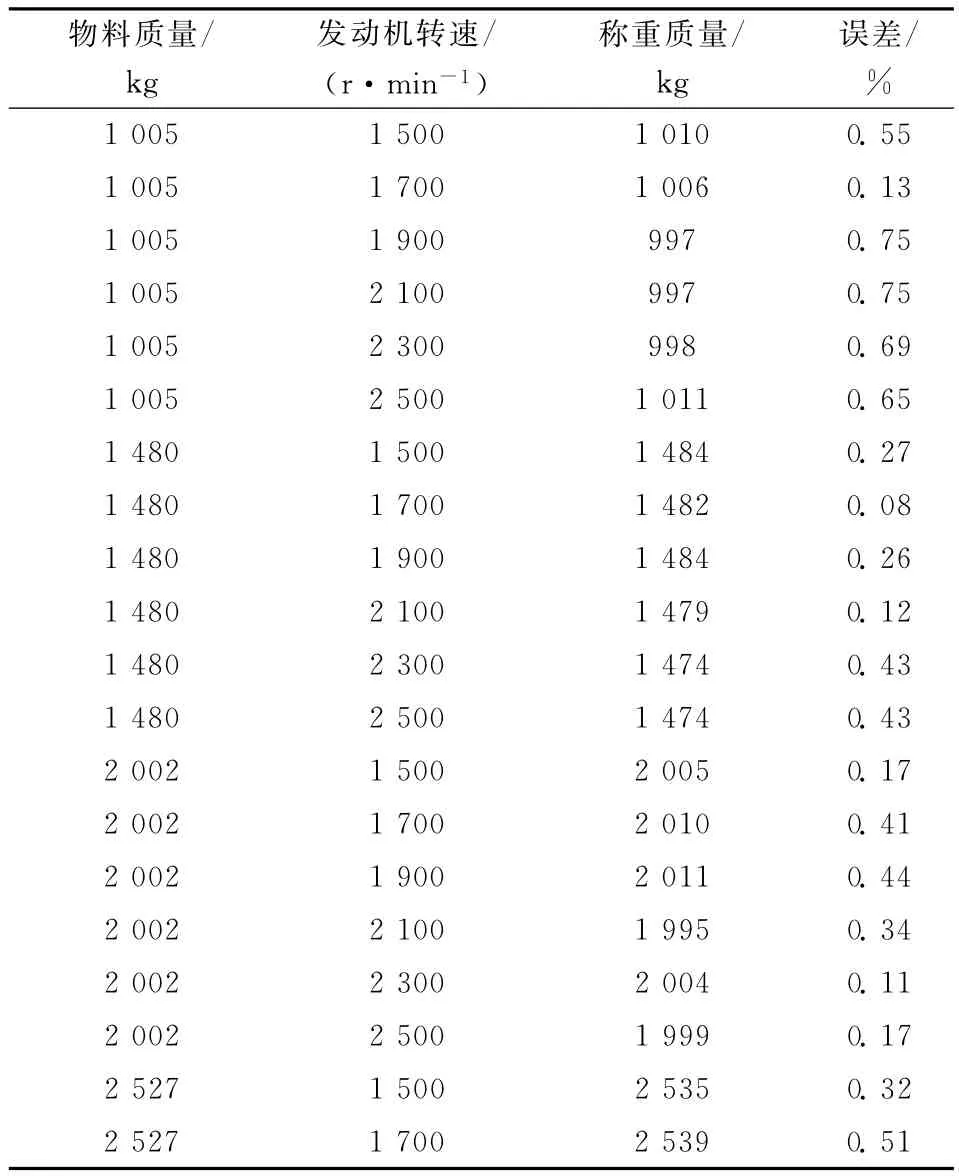
表1 不同的发动机转速下各种负载的称重结果Table 1 The table of weighing in different engine speeds
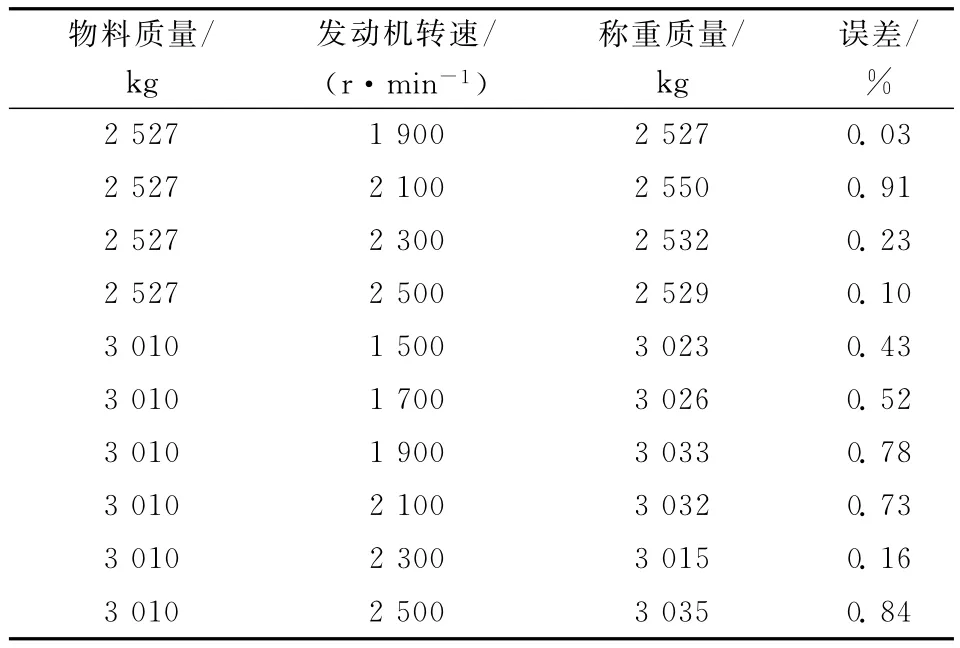
续表1
4 结论
地下铲运机的动态称重是一个较为复杂的系统,影响精度的因素较多。结合试验对此系统进行理论上的深入分析,对提高称重精度具有重要指导的意义。为了实际应用的可靠性和便捷性,对理论公式做了适当的简化,省略了一些参数,研究这些参数并增加必要的传感器,是进一步提高称重精度的方向。
[1]张栋林.地下铲运机[M].北京:冶金工业出版社,2002:47-52.
[2]刘传榕,李学忠.装载机载重测量系统数学模型[J].工程机械,1997(1):11-12.
[3]王伟,王田苗,赵洪明,等.装载机载质量动态测量偏载问题[J].机械工程学报,2007,43(5):106-110.
[4]肖珊,鲁五一,韦晓慧,等.动态称重系统误差修正算法研究[J].传感器与微系统,2007,26(6):80-83.
[5]王伟,王田苗,魏洪兴,等.装载机载重动态测量动力学分析与实现方法[J].中国机械工程,2006,17(22):2333-2338.
[6]王松柏,魏洪兴,王伟.装载机动态称重系统的硬件设计与实验研究[J].制造业自动化,2007,29(1):29-32.
Theoretical research of dynamic weighing system of underground LHD
GUO Xin,ZHAN Kai,GU Hongshu,LI Hengtong
(Beijing General Research Institute of Mining &Metallurgy,Beijing 100160,China)
It is the common method in the practical application that measuring the hydraulic pressure of the lifting cylinder for calculating the quality of ore in the bucket of working LHD.Improving the accuracy is difficult.The first difficulty is due to the objective reasons such as friction damping of the working mechanism,bumpy road,the different gravity of ore in the bucket.The second difficulty is due to theoretical analysis has deficiency on the complex model,which makes the weighing calculation formula is not precise enough,only by using the interpolation and interval measurement to reduce the error.It analyses the mechanics model of LHD in this paper,designs a suitable system in practical application.Especially it finds the rules between the hydraulic pressure and the lifting speed of the arm.It gives a reasonable theoretical explanation and tests the rules with many experiments.
underground LHD;dynamic weighing;frictional drag
TD422.4
Α
1671-4172(2015)04-0075-05
10.3969/j.issn.1671-4172.2015.04.017
国家高技术研究发展计划项目(2011AA060403)
郭鑫(1983-),男,工程师,硕士,矿山机械专业,主要从事矿山机械和无轨车辆设计。

