中国工业用水影响因素的长期动态作用机理
雷玉桃+黎锐锋


摘要
我国正逐步迈向工业大国,工业用水占据总用水量的很大比例,水资源是工业的血脉,但我国的水资源并不丰富,因此工业节水就成为我国的燃眉之急。工业节水政策的制定必须基于对我国工业用水影响因素的动态作用机理的把握之上,因此,本研究正是对此进行深入探究。本文以VAR模型为基础,对中国工业1993-2012年的用水量、总产值以及出口额三个变量的数据进行不影响时序的对数标准化处理,检验出变量间具有相关性系数0.95以上的高度相关性,单位根检验中,变量数据经过了一阶差分之后都是同阶平稳、并且通过了5%水平的协整检验,确定了变量间存在长期稳定的关系。然后,根据变量数据对VAR模型的回归方程进行参数估计以及特征值的检验,确定了VAR模型的参数值和稳定性,继而通过格兰杰因果关系分析确定了变量间的相互作用关系,通过脉冲响应分析图表形象具体地展现了中国工业用水影响因素间的长期动态作用过程,最后通过预测方差分析将各个影响因素对中国工业用水的整体作用进行量化分解分析。通过多层次的综合分析,总结出我国工业用水量及其影响因素(工业总产值和工业制成品出口额)的长期动态作用机理:工业用水量和总产值呈现正相关关系,并且用水量限制了工业经济的进一步增长,因此必须提高工业用水效率;工业出口对用水量的直接影响相对较弱,但是用水量已经制约了我国工业出口的增长,我国面临出口转型的压力;我国的工业用水量对各项影响的反应都有一定的滞后性,因此工业节水需要长期稳定的策略,不能急于求成。
关键词VAR模型;工业用水;脉冲响应分析;作用机理
中图分类号F423 文献标识码A文章编号1002-2104(2015)02-0001-08doi:103969/jissn1002-2104201502001
水资源不仅是维持生命的必需品,更制约着经济的发展。在工业革命之后,工业技术的进步日新月异,不仅推动了全球经济的发展,也促使能源成为了经济发展的原动力。然而20世纪60年代以来,世界各国经济发展迅猛,工业生产用水量、生活用水量、市政用水量、农业生产用水量以及生态用水量的不断增加,水资源短缺的问题日益严重,人们发现水资源成为了经济发展的瓶颈。我国是工业大国,水资源是工业的血脉,我国人均占有水资源量还不到 2 200 m3,居世界第121位,是全球严重缺水的13个国家之一。然而我国的工业用水量却在迅速地逐年攀升:1949年,工业用水量仅为24亿m3,占全国用水量的2.3%,而到1980年,全国工业用水量达到457亿m3,占总用水量的10.3%,到2012年,工业用水量达到1 379.5亿m3,占总用水量的比例上升到22.5%。从1949年到2012年,工业用水量增加了56.5倍,占全国用水量的比例增加了8.78倍。21世纪正是我国经济快速发展的重要时期,水资源作为不可或缺的基础性资源受到了前所未有的重视,如何控制工业用水量也成为了我国发展的首要难题。
1文献综述
为了解决水资源日益短缺的严重问题,国外学者在用水方面做了许多研究:Hoffmann Ierne[1]详细论述水资源作为一种公共物品,研究了适合非洲西海岸地区的水资源管理方法和节水措施。Krause Kate[2]从经济、社会和政策等各个角度进行探讨研究,研究怎样采用措施和策略才能既要实现节水目标,又要经济成本和社会福利成本最低。Dirkzoebl[3]通过对美国水资源用水效率的研究,认为要使水资源可持续利用,必须提高水资源利用效率。这些研究都是根据国外特定的研究对象进行研究,取得了一定的进展。
近年来,中国学者也进行了适应于中国国情的工业用水的研究:祁鲁梁和高红[4]在文章中从可持续发展的角度指出我国工业节水的意义所在,认为工业节水是我国战略发展的必然选择;岳立等[5]利用malmquist指数对我国13个典型的工业省区的工业用水效率进行了研究;杨大楷等[6]对我国的113个重点城市进行了工业循环用水及其影响因素的研究;孙爱军等[7]利用随机前沿模型对我国的工业用水效率和未来耗水量进行了预测研究;贾绍凤等[8]利用库兹涅茨曲线、邓朝晖等[9]利用VAR模型分别对我国的工业用水量与经济发展的关系进行分析。
但是这些研究都缺乏对我国工业用水量的影响因素的分析,也没有指出工业用水量与其影响因素的动态作用机制机理,对实际控制工业用水量的指导意义不足。针对目前我国工业用水量影响因素和动态作用分析相关文献较为缺乏的情况下,本文针对我国的实际情况,以1993-2012年工业用水量以及影响因素的数据为基础,并对数据进行相关性、平稳性检验,然后建立VAR模型进行格兰杰因果关系检验,旨在确立这些影响因素与工业用水量的长期因果关系。通过广义脉冲响应的分析,探究我国工业用水量与其影响因素的动态作用机制机理,并以此来提出一些政策建议来供我国政府部门等决策机构参考。
本文拟采用的VAR模型现已经广泛应用于各项研究之中:杨万平等[10]在对外贸易和FDI对环境污染的影响研究、江涛[11]在证券市场风险的分析研究以及吴振信等[12]在油价波动对我国经济影响的研究中都采用了VAR模型。经过众多学者证明,VAR模型是优秀的计量经济学分析方法,可信度高且具有科学性。
2工业用水量影响因素分析
2.1工业用水量影响因素选择
对于我国的工业用水量的影响因素,本研究选取各类经典经济学中可能的各项生产要素进行相关性和因果关系的检验,其中包括了工业总产值、工业从业人数、工业固定资产投资额、工业企业资产、工业企业个数、工业企业科研经费和人员数、工业企业专利量、工业制成品出口额以及能源消耗总量等。这些可能因素中同时通过了相关性和因果关系检验的是工业总产值和工业制成品出口额这两大极具代表性的影响因素。这也就说明了对我国这一阶段的工业用水量影响最大的就是工业产值和出口,在工业发展的不同阶段用水量会呈现出明显不同的变化趋势,工业总产值最为直观地反映了工业经济的规模情况,而自从改革开放以来,出口是造就我国工业发展的源动力之一,因此,这两项影响因素的选取也是具有充分理论依据的。
2.2数据来源以及标准化处理
本文中工业总产值数据来源于《中国统计年鉴》,并在本文中将工业总产值命名为IGDP(单位:亿元);工业制成品出口额数据来源于《新中国60年统计资料汇编》和《中国统计年鉴》,在本文中命名为EXP(单位:亿美元)。
中华人民共和国水利部官方网站上公布的《中国水资源公报》,是从1997年的数据开始的,并且1997年的数值对比基期是1993年。为了保证数据来源的可信度和权威性,本研究的样本区间确定为1993-2012年。1997-2012年工业用水量数据来源于中华人民共和国水利部网站的《中国水资源公报》,1993-1996年的工业用水量数据是在根据相关统计数据,采用灰度预测的方法进行数据估算得出的。在本文中,工业用水量命名为WAT(单位:亿m3)。
由于各项数据的单位不尽相同,可能存在着较大程度上的波动。因此本文采用对原始的时间序列数据对数化的方式来进行标准化,这样不仅消除了可能存在的异方差,而且不会改变时间序列数据的时序特征。本文将工业总产值、工业制成品出口量以及工业用水量数据标准化处理后的数据分别命名为LNIGDP、LNEXP和LNWAT。
3变量数据的相关性分析和平稳性检验
3.1相关性检验
相关性系数是各项工业用水影响因素对工业用水影响关联程度的体现,相关系数越接近于1,表明影响关联越大。其表达式为:
rxy=∑ni=1(xi-)(yi-)∑ni=1(xi-)2∑ni=1(yi-)2
(1)
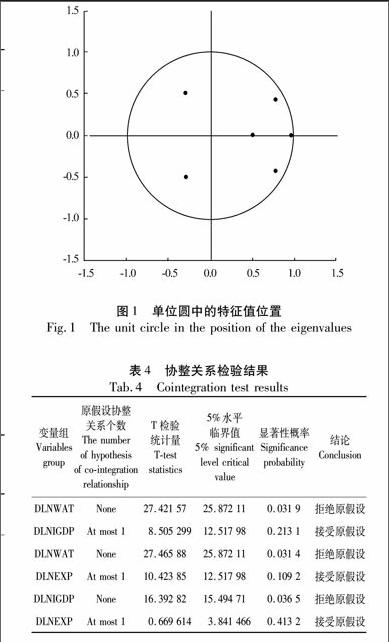
式1中,rxy表示x,y两个变量的相关系数,和分别表示xi和yi的均值。为防止样本数量小、数据的特殊性等方面对结果造成的误差,本文采用双尾检验法验证相关系数检验结果的可靠性并做出决策。当相关系数0.8 3.2数据平稳性检验 在建立VAR模型之前,首先需要检验各项时间序列数据是否平稳,也就是单位根检验。由于传统的单位根检验方法DF检验不够完善,不能保证方程中的残差是白噪声(分布均匀的噪声),因此目前普遍应用的是ADF的单位根检验方法。本文拟选ADF方法对工业用水量及其影响因素变量的时间序列数据进行平稳性检验,检验结果如表1所示: 4工业用水量与其影响因素的长期动态作用机理分析 4.1研究方法 向量自回归模型(Vector Auto Regressive model)是在1980年由美国诺贝尔经济学奖获得者Christopher A.Sims首先提出的,它不以经济理论为基础,而是基于数据的统计性质建立的模型。VAR模型实际上是把系统中每一个内生变量作为系统中所有内生变量的滞后值的函数来构造模型,从而将单变量自回归模型推广到由多元时间序列变量组成的“向量”自回归模型。由于VAR模型是处理多个相关经济指标的分析与预测最容易操作的模型之一,并且在一定的条件下,多元MA和ARMA模型也可转化成VAR模型,因此VAR模型在科学界的应用相当广泛,也取得了较高的声誉。本文采用工业用水量与其影响因素(工业总产值、工业制成品出口额)双变量的VAR模型,然后通过协整分析以及脉冲响应分析,对我国的工业用水量与工业总产值、工业制成品出口额之间的关系进行实证研究。VAR模型的数学表达式为: Yt=∑ni=1AiYt-i+εt+c(2) 式2中,Yt为时间序列构成的向量;c为常数项;n为自回归滞后阶数;Ai为实际序列系数矩阵;εt为白噪声序列向量。在式2中,任意一个VAR模型都可以表示成为一个无限阶的向量MA(∞)过程。具体方法是对于任何一个VAR(k)模型都可以通过友矩阵变换改写成一个VAR(1)模型: 在其他误差项不变的条件下,当第j个变量对应的误差项ujt在t期受到一个单位的冲击后,对第i个内生变量在t+s期造成的影响用ψs中第i行第j列元素 表示。将ψs中第i行第j列元素 看作是滞后期s的函数: yi,t+sujt,S=1,2,3,…(9) 式9被称作脉冲响应函数(impulseresponse function),该函数描述了其他变量在t期及以前各期保持不变的前提下,yi, t+s对 yj, t一次冲击的响应过程。 4.2回归方程参数估计 VAR模型中一个重要的问题就是滞后阶数的确定。在选择滞后阶数 p 时,一方面想使滞后阶数足够大,以便能完整反映所构造模型的动态特征。但是另一方面,滞后阶数越大,需要估计的参数也就越多,模型的自由度将减少。所以通常进行选择时,需要综合考虑,既要有足够数目的滞后项,又要有足够数目的自由度。本文在综合考虑了LR(似然比)检验、AIC信息准则和SC准则之后,将本研究中各变量最大滞后阶数取为2。表2为各变量自回归方程的参数估计。 4.3VAR模型稳定性检验 通过检验,其特征值均小于1,详见表3和图1。 由于本文需要对我国工业经济、出口和用水量的长期动态作用机理机制进行分析,所以简单的关联性分析是不足以证明各变量间是否有长期稳定的动态关系的,还需进行协整关系以及格兰杰因果关系的分析。 4.4协整关系检验和格兰杰因果关系检验 4.4.1协整关系检验 在某种线性组合(协整向量)使得组合时间序列的单整阶数降低时,变量间具有显著的协整关系。协整关系表明了变量间具有长期稳定的均衡关系。本文采用的协整关系检验方法是Johansen协整检验,是一种目前在进行双
变量协整检验中比较普遍的方法,检验结果如表4所示。
通过以上分析,可以得出如下结论:工业用水量、工业总产值以及工业制成品出口总额相互均通过了5%水平的协整检验,存在长期稳定的关系。
4.4.2格兰杰因果关系检验
格兰杰因果分析方法是识别判断两组变量之间是否有因果关系的一般方法,根据格兰杰因果分析的条件,由于三个变量是同阶单整序列,因此可以对其直接进行因果关系检验。检验结果如表5所示。
由表5中可以得出结论:在5%的检验水平下,工业用水量与工业产值、工业制成品出口额都有一定的格兰杰因果关系。这就说明了我国工业用水量跟工业总产值、工业
接受原假设制成品出口额是相互作用、紧密相关的,如果想要评估工业节水措施,这就需要深入探究工业经济、出口与用水量之间的长期动态作用机理,也正是本文的研究意义所在。
4.5脉冲响应分析
脉冲响应函数描述一个内生变量对误差冲击的反应。具体地说,它描述的是在随机误差项上施加一个标准差大小的冲击后对内生变量的当期值和未来值所带来的影响。本文运用脉冲响应函数分析二者之间的冲击响应,这里将冲击响应期设定为10期,分析结果见表6。
4.5.1工业用水量与工业总产值的动态关系分析
工业用水量与工业总产值的脉冲响应分析结果如表6和图2中所示,就工业用水量对工业总产值一个单位冲击的响应来看,LNWAT当期的反应为0,然后在第2期波动后逐步上升,表现出一定的滞后性。在第7期达到了最
接受原假设
大值0.020 396之后,开始平稳下降,在整个分析期内LNWAT对LNIGDP的累计响应值达到了0.119 853,工业总产值对工业用水量的影响为正值,说明了这两者之间的正相关关系,即随着工业经济的增长,工业用水量也会增加,这是符合现实的。而且,从第7期之后就开始呈现下降的趋势,表明在水资源限制的情况下,我国工业经济持续增长是有可能实现的。而就工业总产值对工业用水量一个单位的冲击响应来看,LNIGDP当期的反应就为0.028 782,响应非常迅速,之后快速上升,在第2期就达到了最大值0.046 058,然后迅速下降,然后持续到负值后逐步平稳。在整个分析期内LNIGDP对LNWAT的累计响应值达到了0.038 423,说明了工业总产值虽然对工业用水量的总体影响为正值,但是从第2期之后就一直呈现下降的趋势,最后平稳在负值。意味着我国工业用水效率有很大的提升空间,而且目前工业用水资源制约了工业经济的进一步增长。在目前我国工业用水量难以开源的情况下,工业经济增长的来源显然就必须依靠用水效率的提高了。
4.5.2工业用水量与出口的动态关系分析
工业用水量与工业制成品出口额的脉冲响应分析结果如表6和图3中所示,就工业用水量对工业制成品出口额一个单位冲击的响应来看,LNWAT当期的反应为0,同样表现出一定的滞后性。然后保持上升到第4期时达到最高点0.005 948,之后逐步下降到负值并趋向于平稳。在整个分析期内LNWAT对LNEXP的累计响应值为0.015 288,LNEXP对LNWAT的影响是正值,说明了出口对工业用水量总体上有着正向的影响,而且相较与工业总产值,出口对用水量的影响较为微弱,应该是通过工业总产值间接影响用水量而产生作用。而就工业制成品出口额对工业用水量一个单位的冲击响应来看,LNEXP当期的反应就为0.017 796,响应同样迅速,在第2期就达到了最高值0.075 354,之后就迅速下降,在第6期时达到最低点-0.042 055,之后趋向于稳定。在整个分析期内LNEXP对LNWAT的累计响应值为-0.075 548,为负值,说明了工业用水量的变动对出口产生负面效应,由于工业用水量的制约,使得出口难以为继。
4.6预测方差分解分析
VAR的方差分解能够给出随机扰动项(新息的)相对
重要性信息,它的基本思想是把系统中每个内生变量的变动按其成因分解为与各方程随机新息相关联的各组成部分,以了解各新息对模型内生变量的相对重要性。EViews对于每一个内生变量都计算一个独立的方差分解,计算各变量所引起的方差占内生变量总方差的百分比。3个变量的VAR跨时为10的方差分解见表7。
由表7中可以看出:工业经济增长对工业用水量的贡献较大,末期达到了70%以上,平均值也有36.4%。而且呈现出一直增加的趋势,这一方面反映了工业经济增长与用水量的关系非常紧密,同时也说明了其他影响因素也会通过工业总产值的变化来对用水量进行间接的影响和作用。出口对用水量的贡献率的平均值为5.25%,而且在末期趋向于稳定,说明出口对用水量的影响有限,但是受水资源制约的情况下,工业出口只得自行调整出口模式以控制用水量。而对于用水量对工业经济和出口的贡献率
则是呈现先变大,到达临界值之后逐步降低的趋势。我国工业在刚刚起步的时候处于粗放型经济增长,资源能源在工业经济增长的比重逐年增大,随着我国工业的发展、技
术的进步,工业经济增长的模式和理念也在转变,技术和管理的贡献比重渐渐增大,资源能源在工业增长的贡献也在逐步降低。这与我国工业的发展历程是完全相符的。工业用水量对于工业经济和出口的贡献率平均值也达到了19.13%和11.48%,起到了至关重要的作用,同时也容易看到,用水量的贡献率正在降低,表明通过技术进步和管理改善等方式,确实可以保持工业经济增长的出口同时,减少用水量。
5结论与建议
本文利用中国1993-2012年的时间序列数据,通过相关性分析、VAR模型的格兰杰因果关系、脉冲响应分析等一系列方法,研究了工业总产值以及工业制成品出口额对我国工业用水量的影响和长期动态作用机理机制,得出如下结论和建议:
(1)研究期间内的各项变量标准化后时间序列数据
都具有非常显著的相关性、都是非平稳序列但是它们的一阶差分都为平稳序列,即都是同阶平稳序列。同时通过
VAR模型的分析,它们还具有显著的格兰杰因果关系和协整关系,也就说明这三项变量直接存在着长期稳定的关系,这是本文研究的前提。由于工业经济、工业出口和工业用水量存在长期的关系,探究它们之间的相互影响关系和长期动态作用机理,可以为我国今后在工业节水措施的选择上提供理论依据。
(2)工业用水量对于工业经济和出口的冲击响应都有一定的滞后性,相较于工业经济,出口对于工业用水量的总体直接影响稍显微弱,而且呈现下降至负值然后趋于稳定的趋势。这反映了我国工业出口模式的转变:从一开始的资源能源密集出口型为主开始逐步过渡到了资源能源贡献率很低的出口模式,出口逐渐减少了对用水量的需求。这不仅符合我国的现实情况,也是目前政府正在极力促进的工业产业结构转型的必然结果。既然产业结构转型的成果已然出现,那政府要做的就是坚持到底,要避免因为局部出现的阵痛就畏首畏尾的现象。
(3)从LNIGDP对于LNEXP冲击的反应中可以看出,累计值达到了0.045 614,为正值,也说明了出口对于工业用水量的作用机理不仅仅局限于直接作用,还会通过影响工业总产值来间接影响到工业用水量。因此,对于工业产品出口和用水量之间的相互作用关系是分为直接和间接两个层面的,所以,如果政府能够引导出口的工业产品结构,坚持倡导资源能源贡献率很低的出口模式,可能表面上看直接效果不是非常明显,但是将会通过间接作用影响工业用水量。
(4)由LNEXP对LNWAT的累计响应值为-0.075 548可以看出,工业用水量已经成为工业出口增长的制约条件。所以,我国政府在针对工业产业转型的进程中,不能忽视了出口结构的转型,应该利用一些出口退税等经济手段,有针对性的扶持一些生产过程水耗低、清洁环保的工业产业,限制那些高水耗高污染的工业产业。例如采用政策性补贴的方式来鼓励钢铁、石化、火电和纺织等高耗水行业进行产品和新技术设备的进口,同时利用提高这类产品出口的税费等方法来减少水资源消耗量。
(5)本文通过脉冲响应分析,发现工业用水量的反应有一定的滞后性。所以,这样的政策可能对工业用水量的作用可能不会立竿见影,还会暂时性的影响工业经济增长,有可能导致政府短期内的信心不足,但是从长期的作用的结果来看,这对于工业节水有着深远的影响,并且会反作用与工业经济,促进我国工业的健康发展。
(编辑:田红)
参考文献(References)
[1]Lerne H. A Case Study for the Management of Common Property Resources in Pastoral Areas of West Africa[J].Human Ecology,2004,32(1):77-105.
[2]Kate K. The Demand for Water:Consumer Response to Scarcity[J].Journal of Regulatory Economics,2003,23(2):167-191.
[3]Zoebl D. Is Water Productivity a Useful Concept in Agricultural Water Management [J].Agricultural Water Management,2006, 84(3): 265-273.
[4]祁鲁梁,高红. 浅谈发展工业节水技术提高用水效率[J].中国水利,2005,(7):125-127.[Qi Luliang,Gao Hong.Discuss on Develop Industry Watersaving Technologies for Enhancing Water Efficiency[J]. China Water Kesources,2005,(7):125-127.]
[5]岳立,赵海涛. 环境约束下的中国工业用水效率研究:基于中国13个典型工业省区2003年-2009年数据[J]. 资源科学,2011,33(11):2071-2079.[Yue Li,Zhao Haitao. Chinas Water Use Efficiency of Industry under Environmental Constraints: Based on Data of 13 Industrial Regions During the Period 2003 to 2009[J].Resources Science,2011,33(11):2071-2079.]
[6]杨大楷,汪若君. 工业用水循环利用影响因素差异分析[J].经济问题,2011,(7):82-85.[Yang Dakai,Wang Ruojun. Analysis on Differences of Factors Affecting Water Recycling[J].On Economic Problems, 2011,(7):82-85.]
[7]孙爱军,董增川,王德智. 基于时序的工业用水效率测算与耗水量预测[J].中国矿业大学学报.2007,36(4):547-553.[Sun Aijun,Dong Zengchuan,Wang Dezhi. Prediction of Technical Efficiency and Water Consumption of Industrial Water in China Based on Time Series[J].Journal of China University of Mining & Technology, 2007,36(4):547-553.]
[8]贾绍凤,张士锋,夏军. 工业用水与经济发展的关系:用水库兹涅茨曲线[J].自然资源学报.2004,19(3):279-284.[Jia Shaofeng,Zhang Shifeng,Xia Jun. Relation of Industrial Water Use and Economic DeveloPment:Water Use Kuznets Curve[J]. Journal of Nature Resources, 2004,19(3):279-284.]
[9]邓朝晖,刘洋,薛惠锋. 基于VAR模型的水资源利用与经济增长动态关系研究[J].中国人口·资源与环境.2012,22,(6):128-135.[Deng Zhaohui,Liu yang,Xue Huifeng. Study on the Dynamic Relationship Between Economic Growth and Water Resourcesuse Based on the VAR Model[J].China Population, Resources and Environment, 2012,22,(6):128-135.]
[10]杨万平,袁晓玲. 对外贸易、FDI对环境污染的影响分析:基于中国时间序列的脉冲响应函数分析:1982-2006[J].世界经济研究,2008,(12):62-68.[Yang Wanping,Yuan Xiaoling. The Effect of Foreign Trade and FDI on Environm EntalPollution: An Analysis Based on the Impulse Response Function of Time Series in China:1982-2006[J]. World Economy Study,2008,(12):62-68.]
[11]江涛. 基于GARCH与半参数法VAR模型的证券市场风险的度量和分析:来自中国上海股票市场的经验证据[J].金融研究,2010,(6):103-111.[Jiang Tao. Measurement and Analysis of the Risks in the Stock Market Based on GARCH and Semi Parametric Method VAR Model[J].Finance Study,2010,(6):103-111.]
[12]吴振信,薛冰,王书平. 基于VAR模型的油价波动对我国经济影响分析[J].中国管理科学,2011,19(1):21-28.

