题组教学的实践研究与思考
江苏苏州市吴江区盛泽实验小学(215200) 杨伟琴
所谓题组教学,即克服传统教学一题一例或一课几例的教学模式,在主要教学环节中,将联系密切、方法相通、形式相似的题目,精心设计成具有知识化、系列化、层次化并有利于学生学习的题组。如检查复习时的铺垫型题组,巩固练习时的坡度型题组,揭示规律时的对比型题组,发展能力时的扩展型题组,联结网络时的沟通型题组等。因此,教师可利用题组为学生创设适宜的学习情境,充分展示知识的发生、发展、形成过程和内在联系,引导学生建立良好的认知结构,实现开发学生智力和使学生形成技能、积累数学活动经验之目的。那么,在新课程理念指导下,如何结合教材内容组织学生进行有目的、有计划的题组教学呢?下面,谈谈自己的一些教学实践及思考。
一、基于教材合理设计,形成以旧引新型题组
在新知识教学中,教师可精心设计以旧引新型题组,给学生学习新知做好思维、知识上准备,然后充分展示知识的发生、发展过程,找准新知识的生长点,让学生利用已有的知识结构来同化新知识,实现知识的正迁移,构建深刻、灵动的数学课堂。例如,教学苏教版数学“解决问题的策略——替换”这一内容时,我设计题组进行教学。
1.课前分析
教材中的例1出示了这样一个实际问题:“将一定数量的果汁倒入两种不同的杯子,已知这两种杯子容量之间用分数表示的数量关系,求每种杯子的容量分别是多少。”问题比较复杂,“练一练”中的题目与例题又有很大的区别,思来想去,我觉得课始就开门见山地出示例题进行教学,有些学生的思维肯定跟不上,从而导致课堂气氛不活跃,学生的学习兴趣不高。那么,课堂教学中,怎样切入才能收到事半功倍的效果呢?课间与学生交流时,出示简单的实际问题给他们进行测试,学生都能稍作思考后正确解答。于是,我借助题组进行课堂教学设计,使学生在“复习——新授——变式”的过程中有效学习。
2.题组设计
复习:小明把720毫升的果汁倒入6个同样容量的杯子里,正好倒满,每个杯子的容量是多少毫升?
新授:小明把720毫升的果汁倒入6个小杯和1个大杯里,正好倒满。小杯的容量是大杯的1/3,小杯和大杯的容量各是多少?
变式:小明把720毫升的果汁倒入6个小杯和1个大杯里,正好倒满。大杯的容量比小杯多160毫升,小杯和大杯的容量各是多少?
3.课后思考
(1)激活。
在复习引入环节中,设计以旧引新型题组,既能激活学生头脑中已有的旧知,又能找准学生学习新知的生长点。在这一课教学中,数量关系式“总数/份数=每份数”是解题的基础,通过复习题的解答,可使这一数量关系式清晰地展示在每一位学生面前,利于学生形成自身的知识结构。
(2)生根。
我国有经典的应用替换方法解决的问题,如果用这些题来进行教学,学生只能被动地接受解法,潜在的学习能力得不到开发。这些离生活实际较远的题目虽然能在短时间内引起学生的好奇,却难以维持学生的学习热情,更不会使学生产生学习的需要。因此,课堂教学中,教师可联系生活实际,利用把果汁倒入大杯与小杯的趣味性,调动学生学习的积极性;利用问题“如果把问题变复杂些,你能解决吗”的挑战性,激发学生探究的兴趣;利用例题画出6个小杯和1个大杯,使学生在图中就能看出“如果把1个大杯换成3个小杯,就相当于果汁倒入了9个小杯”“如果把6个小杯换成2个大杯,就相当于果汁倒入了3个大杯”。这样教学,既能借助形象的图画激活学生的生活经验,引导他们经历策略的形成过程,又促进学生原有知识结构的调整和完善,变被动接受为主动探索,从而提高学生解决问题的能力。
(3)成长。
学生通过主动探索,找到解决例1的策略,此时每个人都跃跃欲试,想挑战一番。教师可趁机提出问题:“如果我们把刚才题中的条件变一下,改为‘大杯的容量比小杯多160毫升’,你还能运用假设的策略解决问题吗?”虽然在解决问题过程中可能会遇到阻力、碰到困难,但风雨过后的彩虹更耀眼,困难过后的收获更丰硕。通过比较复习、新授、变式中的这一题组,既引导学生沟通了知识间的联系,又扩展了学生原有的认知结构,形成新的知识网络。
二、基于教材回顾整理,形成知识整合型题组
苏教版小学数学教材在练习题中设计了较多的题组,最常见的有口算题组、计算题组、应用题组等,给学生的学习提供了较大的思维空间。因此,课堂教学中,教师要用好这些题组,通过比较找出其中的联系与区别,帮助学生更好地理解与掌握所学知识。每册数学教材有些题目单独存在于某一练习中,有的是同一单元的不同知识点,有的是不同年级的相通知识点,它们不能以题组的形式出现,但它们之间是相关联、密不可分的。那么,教学中如何把单一的题目转化成不单一的题目呢?我用两个习题进行如下教学。
习题 1:一年级数学教材(上册)第 22页“认识 1、2、3、4、5”后练习一中的第4题。

习题 2:一年级数学教材(上册)第 29页“认识 6、7、8、9、10”后练习二中的第5题。

第一步,各自完成。“学生学习应当是一个生动活泼的、主动的和富有个性的过程”,所以课堂教学中,教师应放手让学生各自完成习题,这样既可以观察每位学生的思考速度、思考结果以及思考状态,又能及时收集学生的反馈信息,找出共性与个性的问题,为汇报交流做好准备。
第二步,交流整理。汇报交流时,我放慢教学节奏,鼓励学生大胆说出自己填的数,并有选择性地进行板书,此时板书的数可以是无序的,等学生把可填的数都说完后再进行整理,使原本无序的答案变为有序的答案。如‘4>□’,□中可从大到小填 3、2、1、0,也可从小到大填 0、1、2、3。这样既使学生感悟到可以填的数不唯一,有多种不同的填法,又让学生经历了一个回顾、整理、有序思考的过程。
第三步,拓展提高。在理清有多少种不同填法与有序排列后,我追问学生最大可以填几、最小可以填几。如‘□>3’,由于学生只认识10以内的数,所以认为□中最大可填10。如果有学生把大于10的数填进去也行,这样可使不同的学生在数学上得到不同的发展。这题填入□中最小的数肯定是4,答案是唯一的。
由浅入深的三步教学,既给了学生独立思考的时间,又给学生提供大胆发言、认真倾听的机会,使学生在思考、回顾、整理、总结、拓展提升的过程中感悟到数学的魅力。
第四步,回顾整合。在高年级的数学教材编排中,一个单元的教学完成后,在复习单元安排一个回顾整理的环节,以帮助学生理清本单元所学的内容。我受这一启发,在完成习题2后,引导学生回顾总结:“大家想一想,我们在学什么内容时也完成过这样的练习?”有些学生的记忆力很好,一下子就想起来了;有的学生学过就忘,一脸茫然。于是我说:“没关系,大家可以翻书找一找、看一看。”学生翻书查找,我在黑板上把这两题板书在一起,问学生:“如果现在让你完成第1题,你想怎样填?”话音刚落,就有学生抢答说:“在‘2﹤□’的方框中,以前我们只能填3、4、5,现在认识了10以内的数,还可以填 6、7、8、9、10。这里最小可以填 3,最大可以填10。”我评价道:“你说得太好了!是的,随着我们知识的不断增长,有些题目的答案也会发生变化。就以‘2﹤□’为例,‘□’中现在可以填这些数,但到学期结束后,你会发现还可以填很多数;到小学毕业时,你会发现可以填的数更多……”学生的学习是需要教师不断引导的,学生所学的知识是需要时常整合的,我的题组教学研究也是不断变化的。
三、基于教材适时拓展,形成比较型题组
新课标、新教材、新教学是当前比较流行的口号,然而教学不是口号,究竟“新”在哪里呢?与以往的教学相比,又有哪些不同呢?具体到每个内容,教学如何实施?就一年级上册“比轻重”的内容而言,我将新旧教材、基本练习与思考题进行对比,结合教材内容与课外拓展,设计了以下一组有层次的习题进行教学,引导学生进行“一对一”“一对几”“几对几”的比较。
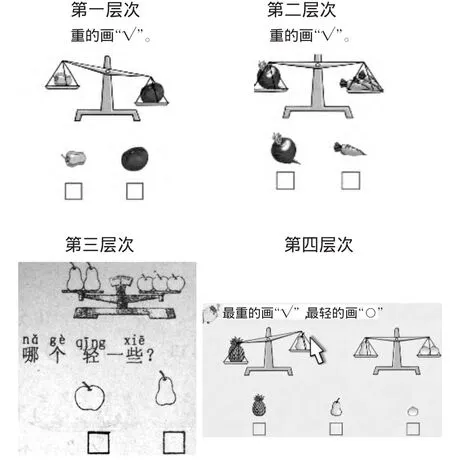
第一层次的题目,一个青椒与一个西红柿“一对一”比较,学生凭直观看到右端向下就可直接判断出西红柿重,一目了然。
第二层次的题目,一个红萝卜与三个胡萝卜一样重,学生也可推出一个红萝卜肯定比一个胡萝卜重,稍作推理就可比较判断。课堂教学中,我没有止步于此,而是引导学生进行两次猜测。第一次猜测,我从天平右盘中拿走两个胡萝卜,问学生:“天平会发生怎样的变化?你知道了什么?”学生的感悟力很强,能在静止的画面中体会天平的倾斜,有的学生还借助肢体语言进行演示。第二次猜测,我在天平左盘中再添上两个红萝卜后问:“这时天平会发生怎样的变化?你知道了什么?”第一次猜测是“一对一”比较,而第二次猜测是“三对三”比较,虽然难度增加,但很多学生都能理解。
第三层次的题目是我课外找来的,初次看到这道习题,觉得用在一年级的课堂上有些不妥,因为用推理的方法思考太难了,学生根本不理解“一个梨与一个半苹果一样重,一个梨就比一个苹果重”。但再次看这道习题,爱不释手,它是我引导学生进行两次猜测后的提升,使“一对一”“三对三”的比较到“几对几”的比较自然过渡。学生不会推理就干脆抛开推理,用直观的、猜测的方法进行思考。
第四层次的题目是教材中的思考题,要进行两次比较,部分学生理解不了。因为进行两次比较,要先根据左边的天平比较得出菠萝重梨轻,再根据右边的天平比较得出一个梨比一个桃重,最后得出菠萝最重,桃最轻。
题组是数学课堂中经常采用的教学形式,既是学生掌握数学知识、形成技能与技巧的重要手段,又是培养学生能力、发展学生智力的重要途径。“路漫漫其修远兮,吾将上下而求索。”

