浅谈学生解题策略的培养
安徽怀宁县教育局(246121) 汪 涛(特级教师)
数学是一门有着严密理论系统和科学方法的学科,知识之间纵横交错,蕴含着千丝万缕的联系。在数学课堂中,适时渗透一题多读、一题多用、一题多化、一题多编、一题多补、一题多问、一题多解等解题策略,不仅可以培养学生思维的灵活性,而且能提高学生解决问题的能力。
一、一题多读
算式,是从具体的数学语言所表达的数量关系中抽象出的符号表达式。课堂教学中,教师应引导学生从多角度抽象出符号表达式,逆向还原为具体的数学语言。这样既有利于显露特定算式的内涵和外延的属性,又有利于学生沟通四则运算内在和外在的联系,架设连接符号算式与数学语言的桥梁。如算式35÷5,教师可启发学生从基本的读法(顺读和逆读)、除法的意义(包含和等分)、乘除的互逆(倍数和因数)、除法的引申(连加和连减)等不同的角度,进行一题多读。如:(1)35除以5的商是多少?(2)5除35的商是多少?(3)把35平均分成5份,每份是多少?(4)35里面包含有多少个5?(5)35是 5的多少倍?(6)5的多少倍是 35?(7)什么数的5倍是35?(8)5乘多少得35……
二、一题多用
用不同的路径解决问题,往往是衡量思维水平的重要标尺。课堂教学中,教师应适当引导学生用新学的知识解决课本的习题,这样既有利于诱发学生的好奇心,展现数学的魅力,又拓展了学生求解的路径。例如,计算7+9,有以下方法:(1)学习20以内的加减法时,可用“拆数凑十”解,即“把7拆成1和6,1和9凑成10,10加6等于16”“把9拆成3和 6,3和 7凑成 10,10加 6等于 16”;(2)学习 9的乘法口诀后,可“化异为同”,即“把7添2看作9,9乘2得18,18减去多加的2等于16”“把9减2看作7,7乘2得14,14加上多减的2等于16”;(3)学习平均数后,可用“移多补少”法解,即“从多的9中移出1补给少的7,得到7和9的平均数8,8 乘 2 得 16”;(4)认识算盘后,可拨珠盘算,即“七上七,九退一进一,结果得 16”;(5)学习用“正”字统计数据后,可用“凑五加剩”算,即“7比5多2,9比5多4,5乘2得10,10加2再加4等于16”……这样一题多用,旧题新用,丰富了解题的路径。
三、一题多化
正确审题是问题解决的前提。解决错综复杂的问题,需要用数学的眼光审视事理,用数学的思维转化事理。例如:“青山村修一条长800米的水渠,第一天修了全长的20%,第二天修了全长的。剩下多少米没有修?”教师可引导学生运用多种形式化事理为数理,进行一题多化。
1.摘录转化

2.作图转化
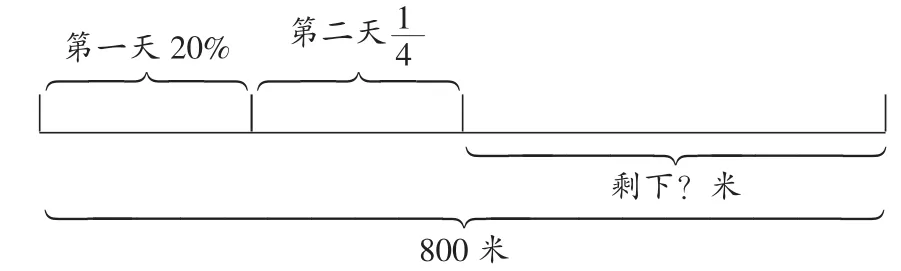
3.换说转化
4.符号转化
5.列表转化
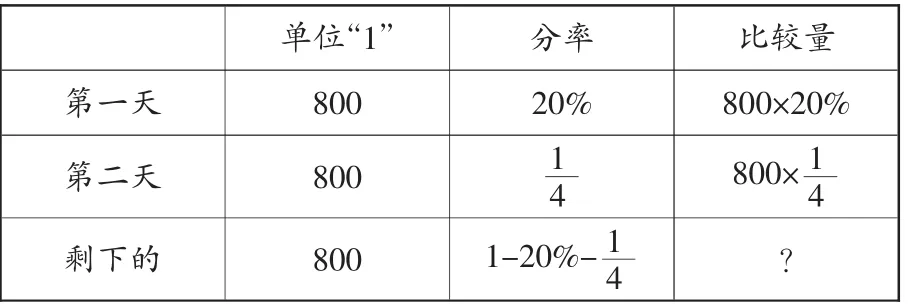
单位“1” 分率 比较量第一天 800 20% 800×20%第二天 800 1 4 800×1 4剩下的 800 1-20%-1 4?
四、一题多编
算式是普遍规律的高度抽象。抽象的算式一旦赋予具体的生活内容,就生成为一道道鲜活的应用问题。课堂教学中,教师可适当引导学生依据抽象的算式,联想具体的实例,多方向编题。这样既有利于密切数学与生活的联系,又有利于显露知识的本质。例如,算式1÷(+),教师可引导学生给算式赋予一项工程、一件工作、一道水渠、一份稿件、一库存粮、一堆石子、一段隧道、一批零件、一架桥梁、一条公路等生活素材,进行一题多编。如:(1)一项工程,单独完成甲要4天,乙要5天,甲乙同时合做需要几天完成?(2)一件工作,单独完成甲要4分钟,乙要5分钟,甲乙同时合做需要几分钟完成?(3)一道水渠,单独修完甲要4周,乙要5周。甲乙同时合修需要几周完成?(4)一份稿件,单独抄完甲要4小时,乙要5小时,甲乙同时合抄需要几小时抄完?(5)一库存粮,单独运完甲要4天,乙要5天。甲乙同时合运需要几天运完?(6)一堆石子重700吨,单独运完甲要4小时,乙要5小时,甲乙同时合运需要几小时运完?(7)一段隧道长800米,单独打通甲要4个月,乙要5个月,甲乙同时合做需几个月完成……
五、一题多补
复杂的生活素材造就了复杂的应用题。应用题结构复杂程度的高低,往往取决于条件隐蔽程度的深浅。课堂教学中,教师可适当引导学生根据已知条件和问题,多途径由浅入深地补充缺少的条件。这样既有利于学生探寻条件与问题之间的因果关系,沟通知识的内在联系,又拓展了知识的应用范围。例如“,红花有8朵,__。黄花有几朵?”题中只有红花的朵数,要求黄花的朵数,就缺少了黄花与红花之间的联系条件。教学时,教师可先引导学生假设黄花的朵数(如5朵),再来寻找黄花与红花之间的可能条件,进行一题多补。如:(1)黄花比红花少3朵;(2)红花比黄花多3朵;(3)黄花比红花的一半多1朵;(4)红花比黄花的2倍少2朵;(5)黄花是红花的;(6)红花是黄花的;(7)黄花比红花少 37.5%;(8)红花比黄花多 60%;(9)红花与黄花朵数的比是8∶5……
六、一题多问
现实生活的多姿多彩决定了数学应用的多变,数学应用的多变往往源自问题的多变。课堂教学中,教师可适当引导学生依据同样的条件,多角度地提出具体的问题。这样,既有利于培养学生究根问底的意识,又有利于训练学生执果溯因的思维品质,使他们形成触类旁通的数学思想。例如:“青山果园栽有两种果树,桃树有500棵,杏树有400棵。__?”教师可启发学生紧扣桃树和杏树的具体数量,沿着“整数——倍数——分数——百分数——比”的路径,进行一题多问。如:(1)桃树比杏树多多少棵?(2)杏树比桃树少多少棵?(3)桃树的棵数是杏树的多少倍?(4)杏树的棵数是桃树的几分之几?(5)桃树的棵数比杏树多百分之几?(6)杏树比桃树少百分之几?(7)桃树占果树总数的百分之几?(8)杏树的棵数占果树总数的百分之几?(9)桃树的棵数与杏树棵数的比是多少?(10)杏树的棵数与果树总数的比是多少……
七、一题多解
解决问题途径的多与少,反映思维发散程度的宽与窄。多途径解决问题,需要搜索知识运用的链接点,提取思维发散的支撑点,寻找问题解决的突破点。例如“:一根钢管截去全长的,正好截去9米,还剩下多少米?”教师可引导学生从分数与份数的联系以及变换单位“1”的角度,进行一题多解。如,化分数为份数:(1)9÷3×2,(2)9÷3×5-9,(3)9×(2÷3),(4)9×(5÷3)-9;以总长为单位;以剩下的长为单位;以截去的长为单位“
课堂教学中,通过多种解题策略的培养,既使学生深刻理解所学知识,又使他们在数学学习上得到不同的发展。

