以单元教学为例谈空间观念培养的整体思考
浙江宁波市广济中心小学(315000) 马霖霞
几乎每一学期数学教材定会安排一至两单元的几何教学内容。几何教学最重要的任务是培养学生的空间观念,现以“长方体和正方体的认识”一单元的教学来谈谈我的实践与思考。
一、尝试先学,整体感知
尝试感知篇的任务是初步了解本单元的学习内容,做好三方面的学习准备,一是后备知识上的准备,二是学习资源材料上的准备,三是学习心理上的准备。学生在动手实践和整体感知中,培养空间观念。以下是“长方体和正方体的认识”尝试感知学案设计:
(一)让我们一起来回忆
1.长方形、正方形的周长、面积的计算公式。
2.面积单位之间的进率是怎样推导出来的?
(二)让我们一起来动手做
1.拆一个牙膏壳,把平面图画下来。
2.玩积木游戏,站在某个角度观察并说出积木的个数。
3、动手尝试做一个长方体和正方体。
(三)让我们一起来看书自学
看书了解长方体、正方体这一单元,了解主要内容。
(四)让我们一起来质疑提问
设计预习作业不是简单笼统的布置预习就完事了,而是教师对教材系统认真的备课,找到这一单元学生学习的知识生长点、关键点和症结点。让学生了解尝试感知的方法和尝试感知的内容。以上设计既解决了知识上的储备,也准备了学习资源,而动手做的过程为学好这一单元打下了知识和能力上的基础,初步感知长方体、正方体知识,是进一步建立空间观念的前提。
二、激活经验,建模感悟
尝试感知让学生有了学习的动力,但感知的层次是粗浅的,知识体系是不完整的,感知的效果因人而异,差异很大。课堂教学应多途径、多手段加强观察与操作,激活学生的经验,使其不断质疑、提炼、整理、升华,逐步对知识形成建模感悟的过程,进一步提高空间观念。
以复习“表面积和体积”为例,看如何完成建模感悟的过程。
师:求下列立体图形的表面积。

(学生独立完成。)
师:如果将这两个立体图形叠在一起,那么这个重叠的立体图形的表面积是多少呢?你该怎么解决?
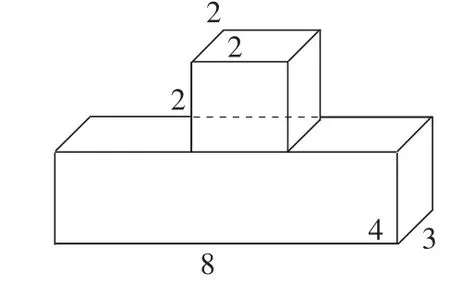
生1:将两个立体图形的表面积加起来,剪掉正方体一个底面的面积。
生2:不对,应该将两个立体图形的表面积加起来,剪掉正方体两个底面的面积。
师:讨论一下,到底剪掉一个呢,还是剪掉两个?为什么?
生3:应该剪掉两个正方体底面的面积,因为两个图形重叠在一起后,长方体的上面也同样有一个和正方体底面一样大小的面给遮住了。
生4:我觉得还可以这样计算:长方体的表面积+正方体四个面的面积
师:怎么解释?
生4:只要把正方体的上面借给长方体中被遮住的部分,就可以理解了。
全班同学都在原来自学的基础上有了新的知识建模:重叠图形表面积减少的是重叠部分的2倍,有时可以借露出的面给遮住的面,方便计算。这样学生对于长方体、正方体表面积的学习有了更深刻的认识。这种面与体之间的转化,让学生在不断的观察中感悟,增强空间观念。
三、激发潜力,拓展提升
在书本知识学习的基础上,适当拓展,可以丰富学生的知识,提高解题的能力,激发学生学习数学的兴趣。因此拓展提升将成为数学学习提升的最后环节,对于学生综合应用数学知识,培养学生的思维能力、创造能力起到了重要的作用。
根据单元“长方体和正方体的认识”的知识点,在教学中渗透下列拓展提升题。

基本知识点 拓展内容 例 子观察展开图,哪些可以围成一个完整的正方体?长方体、正方体的认识看平面图,判断是否能围成立体图长方体、正方体面、棱长、顶点的特点涂色问题人教版P37第11题:27个小正方体拼成的一个大正方体,把它的表面全部涂成绿色,请想一想:(1)没有涂到绿色的小正方体有多少块?(2)一面涂色的小正方体有多少块?(3)两面涂色的小正方体有多少块?(4)三面涂色的小正方体有多少块?(1)把两个棱长为3厘米的正方体拼成一个长方体,表面积比原来两个正方体表面积和减少多少?(2)把2个棱长10厘米的正方体拼成一个大长方体,这个长方体的表面积是多少?(3)从一块长3分米、宽2分米、高1分米的长方体木料上截取一个尽可能大的小正方体,剩下木料的表面积可能是多少?长方体、正方体的体积长方体、正方体的表面积组合图形的表面积变化特殊长方体的体积计算一根长3.5米的木料,把它平均锯成两段,表面积正好增加了2.2立方分米,这根木料的体积是多少?长方体、正方体的综合知识解决生活实际问题数学书各部分的尺寸为:长20厘米、宽15 厘米、厚 0.8 厘米。(1)计划把这样的四本数学课本包装成一包,怎样设计最节省包装纸?(画出草图)(2)算一算,至少需要多大面积的包装纸?(接口处不计)
拿看平面图判断是否能围成立体图这一问题来看,在实际的判断中,学生一直很疑惑,错误率高。教师引导学生:你想不想获得一眼就能看出这样的展开图能否围成平面图形的技巧?学生非常感兴趣,教师借势将任务交给学生,要求完成一个课外作业:准备多个立体图形,按不同的方向打开展开图,将展开图画在纸上,看谁画得多。唯一的一个实践作业让学生欣喜若狂,动手做,动手拆,动手画。然后汇集学生所有的平面图,进行汇总、整理、分类,找到规律。
以上的三环节都体现了学生学习的自主性,预习感知篇以学生独立预习、尝试解决为前提,初步了解知识的来龙去脉,为课堂学习铺垫;建模感悟篇,教师成为引领者,帮助孩子主动建构新旧知识,形成知识网络;拓展提高篇激发孩子几何直观潜能,发展几何思维能力,享受学习几何的快乐与成功。整个单元教学相互联系,相互促进,并始终以观察为主,学生在做中学,学中练,参与体验,参与感悟,最大限度地提高空间观念。

