高精密气动波纹管驱动伺服系统建模与仿真

， ， 　(青岛理工大学 自动化工程学院， 山东 青岛　266500)

引言

气动控制技术是气动技术与自动化控制技术相结合而产生的一项新技术[1]。气动伺服控制系统具有结构简单、价格低廉、输出功率大、环境适应能力强、操作方便等优点，近年来在工业控制领域(如汽车制造业，半导体与电子制造业，生产过程自动化等)得到越来越广泛的应用，已经在工业自动化中占据着重要的地位。气动伺服控制系统与传统的气动系统相比，可以非常方便的实现柔性定位和无级调速[2]。目前，许多学者都在对气动伺服控制系统进行研究。典型的气动伺服控制系统多采用气缸或马达作为驱动执行器，但是气缸活塞受多种摩擦力影响不利于精密控制，限制了定位精度的进一步提高。

金属波纹管作为驱动执行机构，近年来已有学者对其进行了一定的研究，其工作寿命和机械特性已经在实验中得到验证[3]。在国外，Toshinori Fujita等采用金属波纹管设计了超精密运动平台，精动控制精度达到20 nm,验证了波纹管作为驱动机构的可行性。使用金属波纹管作为单一驱动机构设计新型气动伺服系统，对气动比例伺服阀，金属波纹管驱动执行器的特性进行了分析，并建立气动伺服系统的动力学模型进行了仿真研究。

1　实验系统的组成及原理

实验系统由金属波纹管式气动执行器、电气比例伺服阀、位移传感器和A/D、D/A转换模块组成。

金属波纹管是一种挠性、薄壁、有横向波纹的管壳零件。依靠内部气体压力的变化产生伸缩运动，产生位移。按其波形可分为“U”型、“Ω”型、“S”型波纹管等。“U”型波纹管能够承受较高的压力，并能吸收较大的位移[4]，本实验采用单层U型金属波纹管作为单一驱动执行机构。

本实验的比例阀采用ITV-2050-212S5型电/气比例阀，这是一种带有高速开关阀的先导式压力型电/气比例阀，压力反馈可以直接引入阀内，提高系统的稳态精度, 改善系统的动态性能, 使系统的刚性大大提高。

位移传感器采用Mercury3500光栅位移传感器，具有抗电磁干扰能力强、高速度、小尺寸和使用灵活方便的优势，配合PC端软件，用户可以自己定制编码器的分辨率和工作频率，分辨率最高可以达到5 nm。

A/D、D/A转换由stm32单片机来完成。

实验系统的组成框图如图1所示。

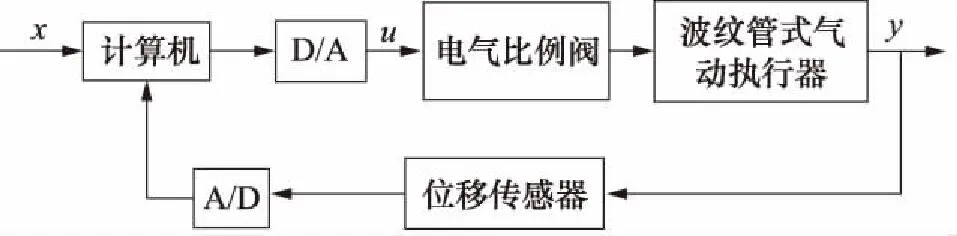
图1　系统组成框图

为了简化计算，更好地分析和研究气动伺服控制系统的特性，现做如下假设[5]：

(1) 所用工作介质为理想气体，满足理想气体状态方程pV=nRT；

(2) 供气压力ps和温度T恒定；

(3) 腔室中的气体热力过程为准静态过程；

(4) 波纹管管腔中的气体是均匀的，每一瞬时腔中各点的参数相等；

(5) 波纹管管腔与外界之间没有泄漏；

(6) 气体在流过阀口或其他节流孔时的流动状态均为等熵绝热过程。

2　比例阀，波纹管动态特性基本方程

2.1　波纹管执行器管腔流量方程

因波纹管管腔内气体认为是理想气体，故气体的动能、势能忽略不计。同时气体与外界为绝热状态，所以根据热力学第一定律，可得到波纹管管腔的能量平衡方程为[6]：

hdM=dU+dW

于是运动过程中，波纹管腔的能量变化方程为：

式中:h—— 气源气体的比焓

A—— 波纹管管腔有效受压面积

Qm1—— 进入金属波纹管腔室的气体质量流量

x—— 金属波纹管伸长位移

T—— 气体温度

R —— 气体常数

k—— 气体绝热指数，为气体定压比热与定容比热之比

2.2　比例阀的阀口流量方程

气体通过阀口的过程十分复杂，在气动技术中通常把气流通过各种阀类元件和管道所组成的管道系统抽象成一个等效的收缩喷嘴或节流小孔来计算[7]。由假设条件，将通过阀口的气体流动过程近似为理想气体通过收缩喷管的一维等熵流动，采用 Sanville.F.E 流量公式得：

2.3　波纹管动力学方程

由牛顿第二运动定律可得气动伺服系统的负载动力学方程为：

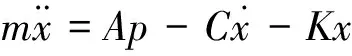
式中：m—— 负载质量

A—— 波纹管的受力面积

p—— 波纹管内气压

C—— 波纹管的阻尼系数

就这一现象，董同龢先生认为，“像这样粹而不杂的现象到底不够普遍的，很难引出什么推论。其实从音理方面讲，舌面音就说是塞音的话，总难免带一些塞擦音的色彩。由这一层关系，ts′-系字可以较多与ts-系接触不是很自然的吗？”[5]

K—— 波纹管的弹性刚度

x—— 波纹管伸长位移

3　仿真模型建立与分析

根据建立的动力学方程通过MATLAB 2012b软件Simulink模块对实验系统进行建模。图2为波纹管管腔流量模型，图3为比例阀阀口流量模型，图4为波纹管伸缩动力学模型。这样就得到了系统的动态模型。运用控制算法对其控制仿真就能够得到输入信号与仿真输出的比较图。PID控制以其简单、有效、实用的特性普遍应用于气动位置伺服系统控制中[8]。图5为典型PID控制系统方块图：

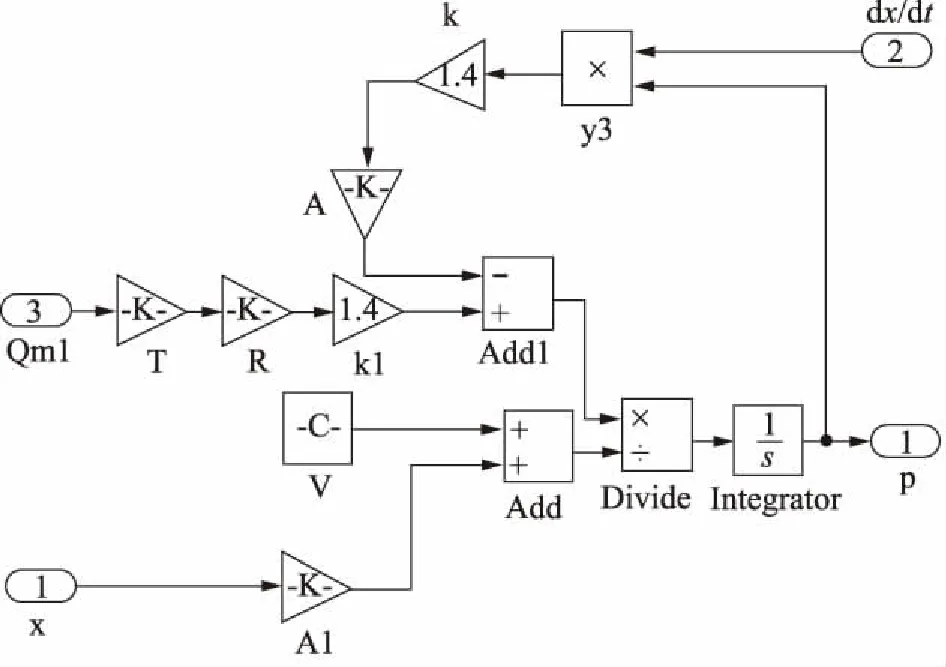
图2　波纹管管腔流量建模图

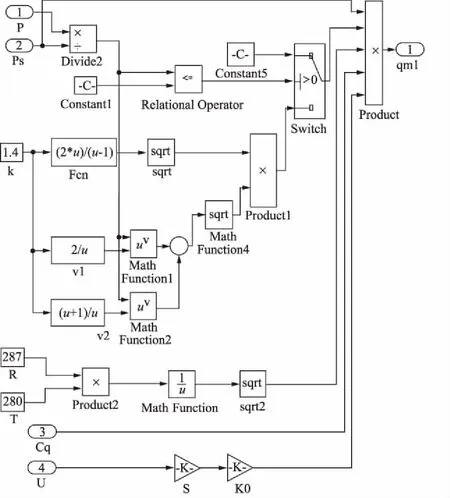
图3　比例阀阀口流量建模图

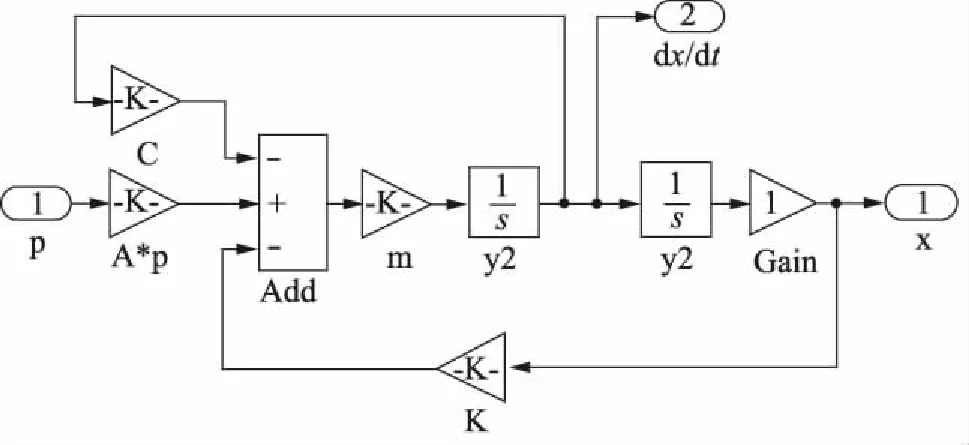
图4　波纹管负载动力方程建模图

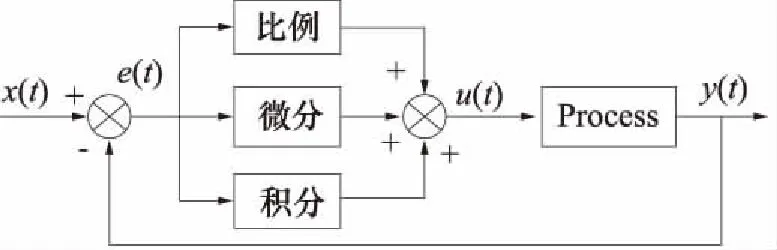
图5　典型PID控制的闭环系统方块图

本次实验就使用典型PID控制对系统进行控制。本实验系统中的参数设置为：气源压力ps为700 kPa，负载m为0.8 kg,气体常数R为287 J/kg·K，气体绝热指数k为1.4，气体温度T为280 K，波纹管管腔有效受力面积A为0.00224 m2，波纹管阻尼系数C为380.5 N·s/m,波纹管弹性刚度K为248800 N/m。

图6为系统整体建模图。

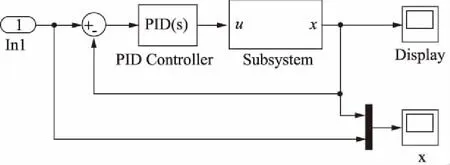
图6　实验系统仿真建模图

对气动伺服系统进行动态特性的测试时，可以对系统施加不同幅值的阶跃，正弦信号，测得不同的输出。图7为给定位移为1 mm阶跃响应的给定曲线与仿真曲线比较图。图8为给定振幅为1.5 mm正弦响应的给定曲线与仿真曲线比较图。

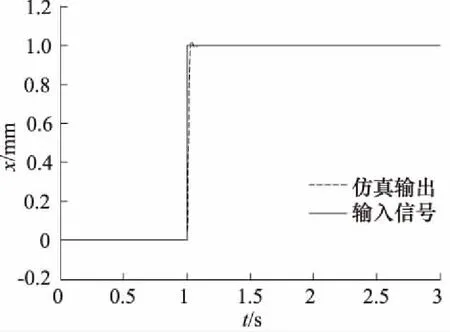
图7　阶跃响应曲线比较图

图9为给定振幅为1 mm正弦曲线时，给定曲线、仿真曲线及实际输出的比较图，其中实线为给定曲线，虚线为仿真曲线，点线为试验实际输出曲线。由上述图表比较结果可以看出，所建气动伺服系统的动力学模型数据与试验数据是相吻合的，证明了所建数学模型是正确的，同时还表明所建系统的准确性是较强的。

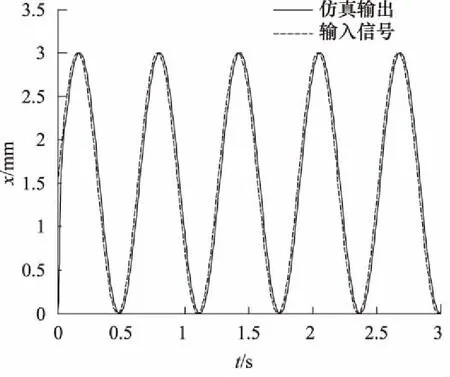
图8　正弦响应曲线比较图

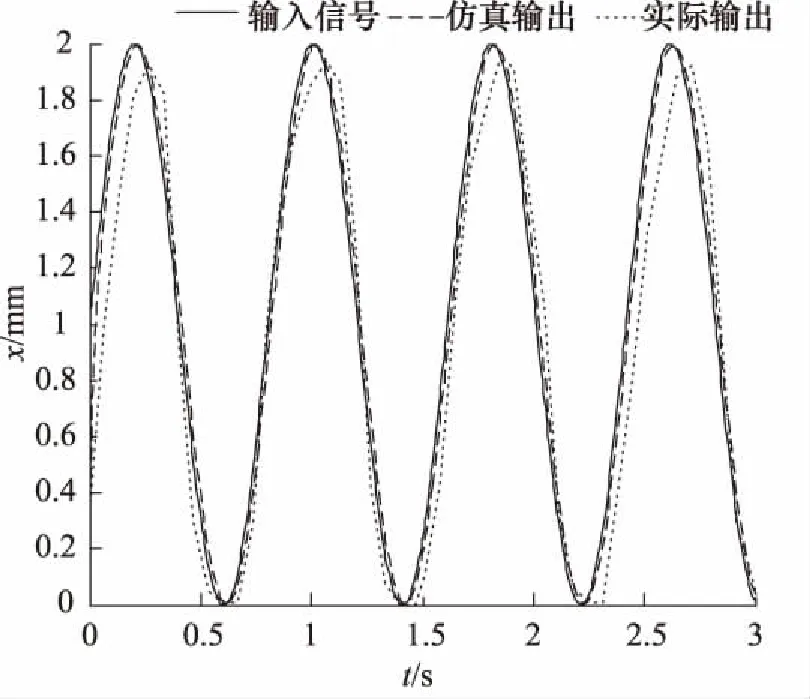
图9　实际曲线比较图

4　结论

对一种新型的由金属波纹管驱动的气动位置系统进行了动力学建模，并使用传统PID控制算法通过MATLAB仿真做了基本的阶跃和正弦的实验研究， 与实际试验结果进行比较分解， 验证了所建模型的有效性。对气动波纹管驱动的伺服系统数学模型的建立和仿真结果的分析，为进一步对系统进行分析，采用更合适的控制算法，提高系统的定位精度打下了良好的基础。

参考文献：

[1]万明亮.基于ARM的气动伺服系统设计与研究[D].江西：江西理工大学，2012.

[2]董晓倩，郭淑娟.气动比例/伺服系统的建模研究[J].机床与液压，2003,(1):222-223.

[3]刘延俊，李兆文，陈正洪.气动比例位置系统的建模与仿真研究[J].机床与液压,2002,(4):56-57.

[4]田艳兵,等.波纹管驱动超精密定位平台建模及复合控制[J].电机与控制学报,2014,18(7):94-100.

[5]周洪．气动伺服定位技术及其应用[J]．液压与气动，1999,(1)：25-29．

[6]牛玉华.“U”型波纹管膨胀节的设计研究[D].南京：东南大学,2006.

[7]王宣银.气动位置伺服系统PID控制的研究[J].机床与液压，2001,(2):49

[8]吴金波.高压伺服气缸及其高压气动位置伺服系统的研究[D].武汉：华中科技大学,2002.

[9]高恒,尚群立.气动位置伺服系统建模与PID控制仿真研究[J].机械制造,2009,47(543):21-23.