基于MATLAB/Simulink液压伺服系统辨识仿真

　，

(南京理工大学 机械工程学院， 江苏 南京　210094)

引言

液压伺服系统[1]的产生和发展已经历经了半个多世纪的历史，其具有反应快、刚度大、结构紧凑、惯性小和精度高等的优点，如今已经在各行各业，不论从国防到民用，从工业到农业都得到了广泛的应用。随着科学技术的不断进步，人们在应用过程中对于液压伺服系统的要求也不断的提高。由于其具有很高的非线性以及模型不确定性[2]，在应用过程中时增大了复杂性和难度，因此在对其进行控制研究和故障检测时，对液压伺服系统进行系统参数辨识有很大的必要。

系统辨识，L.Ljung[3]定义为辨识有3个要素——数据、模型类和准则，辨识就是按照某个准则在模型类中选择与数据拟合最好的模型。在辨识研究中，通过仿真或者实验得到系统的输入、输出，根据系统本身的特性，确定最贴切实际的模型参数。辨识的方法有很多种，在工程中的应用也层出不穷。赵盼[4]、王少萍采用ODE的参数辨识方法，应用于液压伺服系统的灰箱建模。在电机辨识中，喻寿益[5]等用无功功率模型辨识电机转子的时间常数；G.Garcia[6]通过降阶的扩展卡尔曼方法把磁链和转子电阻作为输入组成降阶模型进行辨识。液压伺服系统具有很高的非线性，在建立液压模型时，有些参数很难获得。本研究基于MATLAB/Simulink针对对称液压缸及研究的液压伺服系统，建立线性化的液压模型，运用最小二乘法采用开环的方式对液压模型的黏性阻尼系数、泄漏系数、油液弹性模量、伺服阀时间常数进行仿真研究，为以后的控制和故障检测打下理论基础。

1　建立数学模型

1.1　系统物理模型

在对系统辨识研究前，首先要建立液压伺服系统的数学模型，模型的建立对于研究系统参数具有很重要的意义。外负载力F作用于活塞杆上，活塞杆由油液通过伺服阀控制其实现预期的运动。对称的阀控缸液压伺服系统，液压缸与负载组成的系统可视作一质量-弹簧-阻尼的二阶振荡系统[7]。其物理模型原理图如图1所示。

图1　液压伺服系统原理图

1.2　系统数学模型

系统动力机构固有频率低于50 Hz，因此电液伺服阀的传递函数可以表示为[8]：

(1)

式中，K=KuKa，Ku为电液伺服阀流量增益；Ka为放大器增益；τ为电液伺服阀时间常数；xv为阀芯位移；u为输入电压。

液压缸的动力学模型可以描述为：

(2)

式中,m为液压杆的质量；A为活塞面积；pL=p1-p2，表示负载压力；B为黏性阻尼系数；K为弹性刚度系数；F为外负载力；在这个液压系统中K=0，F=0。

将式(2)进行Laplace变换得：

(3)

忽略液压缸内泄漏，流量方程可以表示为：

(4)

(5)

式中：βe为油液弹性模量；V1、V2分别为液压缸两腔的容积，V1=V0+Ax，V2=V0-Ax，V0为液压缸容积；cip为液压缸内泄漏系数。

将式(4)减式(5)得：

(6)

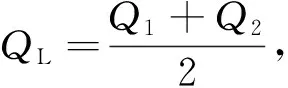
由于这个系统pL≤pS，因此可以将流量方程线性化QL=Kvxv[9]。

由式(1)～式(6)建立液压伺服系统数学模型，并在Simulink中搭建模型如图2所示。

(7)

式中：

a=KKVA

(8)

(9)

(10)

(11)

b4=A2+cipB

(12)

图2　对称缸液压伺服系统Simulink模型

将式(7)双线性变换得：

(13)

式中：T为采样周期；

c1=8b1+4b2T+2b3T2+b4T3

(14)

c2=-32b1-8b2T+2b4T3

(15)

c3=48b1-4b3T2

(16)

c4=-32b1+8b2T-2b4T3

(17)

c5=-8b1+4b2T-2b3T2+b4T3

(18)

2　液压伺服系统辨识

2.1　激励信号

在辨识研究中，为了使系统可辨识，要求在辨识时间内系统的动态必须被输入信号持续激励，即输入信号能够充分激励系统特性[10]。

在系统辨识中比较广泛采用的是伪随机二位式信号(PRBS)，是一组取值为-1,1的序列，不仅有近似白噪声的性质，而且工程上易于实现，如图3所示。

图3　伪随机二位式信号示例图

2.2　最小二乘法

最小二乘法是一种经典有效的古老的用于系统辨识的方法。其原理是使对系统每次实际观测值与计算值差的平方乘以其度量精度的数值后的和最小。不需要估计变量的任何统计特性，具有无偏性和一致性。

设一个系统模型有如下关系：

y(k)=φT(k)θ+ξ(k)

式中，ξ(k)为白噪声；φT(k)=[-y(k-1),…,-y(k-n1),u(k-d),…,u(k-d-n2)]T为测量数据向量；θ=[θ1,θ2,…,θn]T为系统参数。

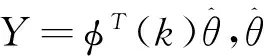
随着观测次数的增加，矩阵求逆的计算量也增大，增加了计算得储存空间，若φT不满秩，则出现病态无法求逆，因此一般多采用最小二乘的在线辨识。其基本思想为：

新的估计值θ(k)=老的估计值θ(k-1)+修正值。

设第j次观测Yj、φj，

在j次基础上加

则

设

因此，最小二乘法的在线辨识算法：

3　仿真结果与分析

3.1　仿真数据设定

针对某机构液压伺服系统，对其进行辨识仿真。在仿真时系统输入为幅度为0.3的一种PRBS信号。其输入输出曲线如图4所示。针对液压开环系统进行仿真，仿真时长为5 s，采样周期为0.01 s。取500个采样点辨识伺服阀时间常数τ、油液弹性模量βe、黏性阻尼系数B和内泄漏系数cip。辨识结果见图5。参数辨识值与该液压伺服系统真值见表1。

图4　系统输入曲线图

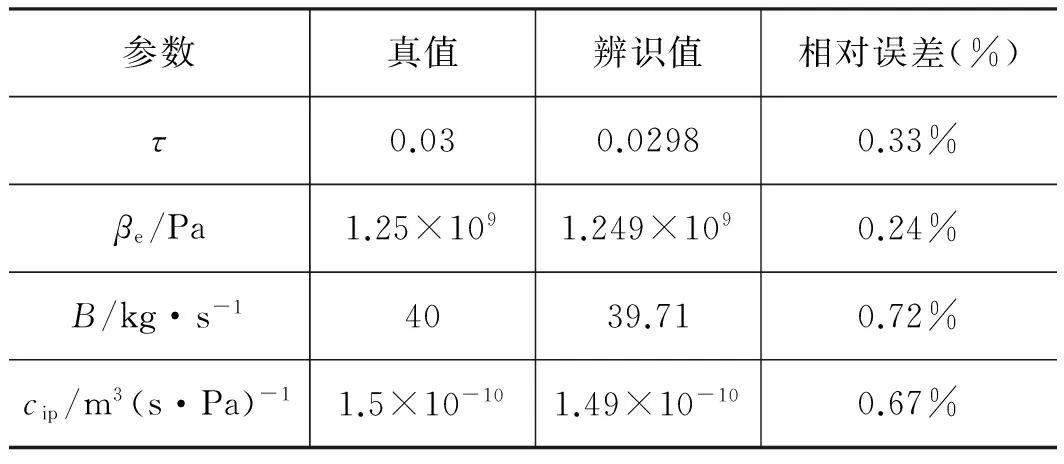
参数真值辨识值相对误差(%)τ0.030.02980.33%βe/Pa1.25×1091.249×1090.24%B/kg·s-14039.710.72%cip/m3(s·Pa)-11.5×10-101.49×10-100.67%

图5　参数τ、βe、B、cip辨识结果曲线图

3.2　结果分析

由表中数据可以看出，使用最小二乘法对系统进行辨识仿真得出的结果。在使用最小二乘算法进行迭代时，当迭代到150步左右时，参数收敛到真值域内，且误差小于1%，对液压伺服系统的模型具有较好的辨识效果。存在误差可能因素为： ① 在仿真时由于噪声对系统的干扰； ② 由于随着数据的增大，迭代次数不断增大，最小二乘法会出现“数据饱和”的现象，使得增益矩阵K(k)趋于零，逐渐失去了修正能力。

4　结论

采用最小二乘法对液压伺服系统，建立线性化的对称缸数学模型，针对某一液压伺服系统进行参数辨识仿真，将辨识参数结果与系统真值进行对比和相关误差的计算比较，说明将这种方法应用在液压伺服系统中能够较好的识别出系统的参数。同时也说明将液压伺服系统高度非线性模型线性化处理，能够取得较好的辨识效果。为在实际工程应用中对液压模型进行简化处理，提供了一个理论参考方法，为今后的控制和故障检测打下基础。

参考文献：

[1]刘长年.液压伺服系统优化设计理论[M].北京：北京冶金工业出版社, 1989.

[2]B Yao, G T C Chiu, J T Reedy. Nonlinear Adaptive Robust Control of One-dof Electro-hydraulic Servo Systems[J].Proc. ASME IMECE, 1997,(4):191-197.

[3]Ljung L.Convergence Analysis of Parametric Identification Methods[J].IEEE Trans.Automatic Con-trol, 1978, 23(5):770-783.

[4]赵盼，王少萍.基于ODE参数辨识的液压伺服系统灰箱建模[J].航空学报, 2013, 34(1):187-196.

[5]喻寿益，张艳存，高金生，等.基于无功功率模型的异步电机矢量控制系统转子时间常数辨识[J].中南大学学报(自然科学版)，2009，40(5)：1318-1322.

[6]G Garcia Soto，E Mendes A Razek. Reduced-order Observers for Rotor Flux,Rotor Resistance and Speed Estimation for Vector Controlled Induction Motor Drives Using the Extended Kalman Filter Technique[J].IEEE Proceedings: Electric Power Applications, 1999, 146(3):282-288.

[7]王勇勤，张云飞，严兴春,等.伺服阀非线性特性建模的液压弯辊系统动态特性[J].重庆大学学报(自然科学版), 2005, 28(11):5-7.

[8]韩桂华,邵俊鹏,董玉红,等.基于xPC技术的液压伺服系统模型辨识研究[J].液压与气动, 2007, (7):16-20.

[9]Yili Qian, Ge Ou, Amin Maghareh, Shirley J Dyke.Parametric Identification of a Servo-hydraulic Actuator for Real-time Hybrid Simulation[J].Mechanical Systems and Signal Processing, 2014, 48(1):260-273.

[10]候媛彬，汪梅，王立琦.系统辨识及其MATLAB仿真[M].北京：科学出版社, 2004.