压力补偿变间隙密封液压缸研究

， 　， 　， 　

(北京航天发射技术研究所， 北京　100076)

引言

恒间隙密封伺服液压缸虽然有摩擦力小、频率响应高、低速稳定性好等优点，但其泄漏量会随着压力的上升而迅速增大，容积效率低，为了解决这一矛盾，我们提出了一种压力补偿变间隙密封伺服液压缸。

1　压力补偿变间隙密封液压缸原理

压力补偿变间隙密封伺服液压缸结构原理如图1所示，其结构特点是在活塞和导向套上设计有微小唇边，当工作腔压力升高时，唇边在内外压差作用下产生微小变形，使间隙量减小，从而达到减小泄漏量的目的。

活塞在运动过程中受周期性高低压液压油作用，在液压油作用下，活塞唇边内表面受到恒定压力的作用， 外表面受到递减压力作用[1]。 根据材料力学、 弹塑性力学原理，若活塞唇边内表面受力大于外表面，则活塞唇边向外部扩张， 间隙量减小。 且在弹性变形范围内，活塞唇边的变形量随内、外表面受力差值的增大而增大，从而实现密封间隙的压力补偿。

1.缸体　2.活塞　3.活塞均压槽　4.活塞杆　5.导向套　6.泄油孔7.缸盖　8.导向套均压槽　9.活塞唇边　10.导向套唇边图1　压力补偿变间隙密封液压缸结构原理图

2　变间隙密封液压缸活塞唇边变形数学模型

为方便计算，从唇边截取一段轴向单元，将其变形简化成悬臂梁的变形来进行求解[2]，其受力分析如图2所示。考虑到活塞的运动特性，在分析唇边变形时，忽略其轴向受力[3]。

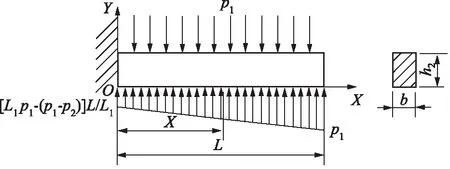
图2　变形活塞唇边受力分析

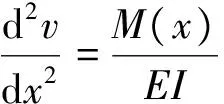
图3　活塞唇边受力的合力

X处截面惯性矩：

(1)

线性载荷最大处为：

(2)

式中：L1为密封间隙长度；p1为工作腔压力；p2为非工作腔压力。

固定端的支反力：

(3)

固定端弯矩：

(4)

X截面的弯矩：

(5)

由挠曲线的近似微分方程在此线性载荷作用下引起的挠度为：

(6)

在固定端，转角和挠度均为零，即x=0时，y(0)=0，y′(0)=0，因此可确定积分常数：

(7)

(8)

整理得：

y(x)=-(p1-p2)(L-x)(5L4-(L-x)4)/

(9)

3　自补偿变形活塞的仿真分析

活塞唇边受力变形时，密封间隙的形状发生改变，间隙内的压力分布也发生变化。压力的变化又反作用于唇边，从而对唇边的变形产生影响。因而间隙泄漏量的变化是唇边变形和间隙内流场相互作用并达到平衡后的结果。因此可以通过采用阶梯压力下降技术，获得合理的压力分布，从而得到理想的变形，获得合理的泄漏量。

对间隙密封液压缸变形活塞进行仿真分析，三维模型如图4所示。活塞直径D为50 mm，密封面长度L1为40 mm,活塞唇边长度L为10 mm,唇边厚度h2为2 mm。为得到合适的压力分布，密封面开有6个1.5 mm×0.8 mm的均压槽，第一道均压槽距唇边端面3.5 mm，第二道均压槽距唇边端面15 mm，其余均压槽均布，并且用一条相同宽深的轴向槽将均压槽连通，间隙量设为15 μm，p1=20 MPa，p2=0 MPa。

图4　仿真模型

对间隙内的流场进行仿真分析，活塞外表面所受压力如图5所示。

将图5所示压力曲线施加到仿真模型上进行ANSYS有限元分析。结果显示，压差为20 MPa时，活塞唇边的总变形量最大约为8 μm，如图6所示。沿活塞径向方向的最大变形量约为7.1 μm，如图7所示。

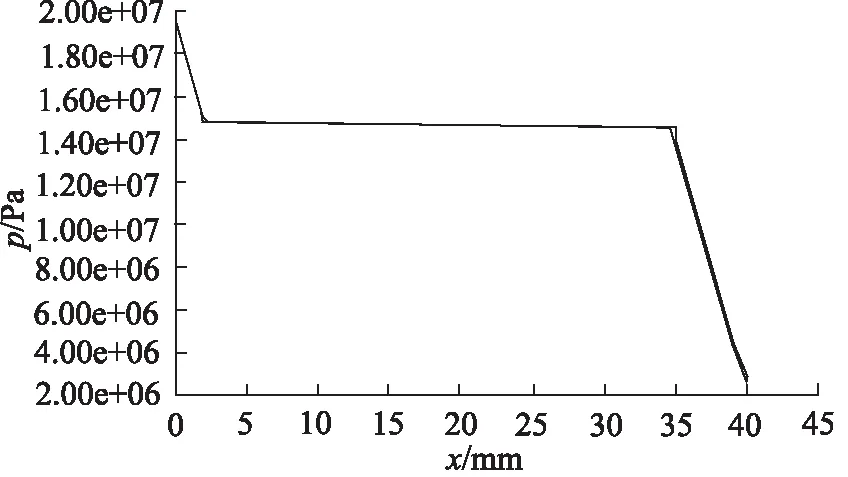
图5　密封间隙内的压力分布

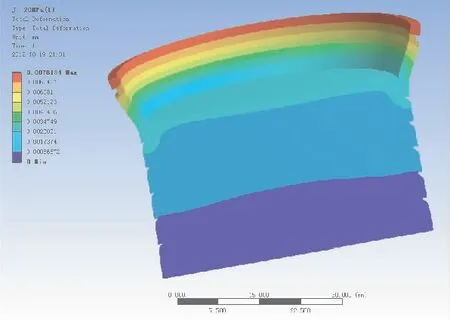
图6　活塞唇边总变形量

图7　活塞唇边径向方向的变形量

由图可知，唇边的最大变形发生在中部附近，并且活塞除去唇边之外的其他部分变形量与唇边相比很小，可以忽略。这说明变形活塞密封间隙的密封效果，主要由活塞唇边的变形性能决定。

4　变间隙密封液压缸试验研究

对压力补偿变间隙密封液压缸的泄漏量进行了试验测试，试验用液压缸简图如图8所示，变形活塞结构与图4所示模型一致，测试结果如图9所示。

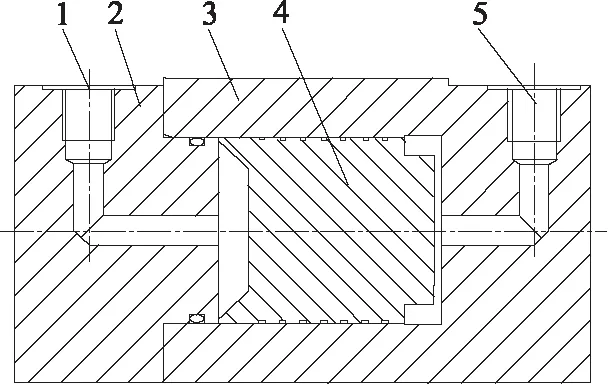
1.进油口　2.缸盖　3.缸体　4.变形活塞　5.回油口图8　变形活塞间隙密封液压缸

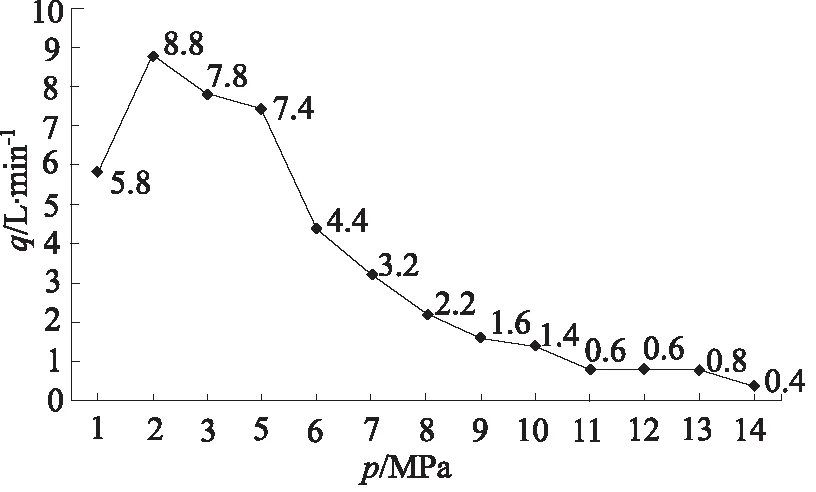
图9　泄漏量-压差曲线

由于试验设备限制，试验结果并不能精确验证活塞变形量的大小，但可以根据间隙泄漏量随压力升高的变化，推断活塞的变形趋势。由试验结果可知，随着试验压力的升高，间隙泄漏量逐渐减小，表明活塞唇边随压力的升高，变形量增加。该种结构的变形活塞，能够有效减小间隙密封液压缸的泄漏量。

分析认为，间隙两端压差小于2 MPa时，活塞唇边变形量极其微小，泄漏量随间隙两端压差的增大而增加；压差大于2 MPa后，活塞唇边产生明显变形，密封间隙厚度减小，由间隙减小导致的泄漏量减少大于间隙两端压差增大导致的泄漏增加量；当压力达到11 MPa以后，间隙减小导致的泄漏量减少与间隙两端压差增大导致的泄漏增加量基本持平，间隙泄漏量基本恒定。

5　结论

压力补偿变间隙密封液压缸，其内泄漏量随间隙两端压差的增大而减小，并最终趋于恒定。通过采用阶梯压力下降技术得到合理的活塞变形量，将泄漏量控制在合理的范围内。压力补偿变间隙密封技术可推广应用于其他需要微小变形的液压元件中，以提高液压元件的性能。

参考文献：

[1]H. 欧特尔，等[德]. 普朗特流体力学基础[M].朱自强，钱翼稷，李宗瑞译．北京：科学出版社，2011.

[2]聂毓琴，孟广伟．材料力学[M]．北京：机械工业出版社，2004.

[3]Vivek Kumar，Mani Mehra. Wavelet Optimized Finiter Difference Method Using Interpolating Wavelets for Self-adjoint Singularly Perturbed Problems[J]. Journal of Computational and Applied Mathematics,2009,230(2):803-812.

[4]杨桂通．弹性力学[M]．北京：高等教育出版社，2010．

[5]杨文军,陈新元,邓江洪.间隙密封液压缸的活塞卡紧力分析[J].液压与气动,2012,(9):107-109.

[6]鲁腊福,陈昶龙,曾良才,等.间隙密封液压缸活塞杆静压支承特性仿真分析[J].液压与气动,2012,(12):126-129.